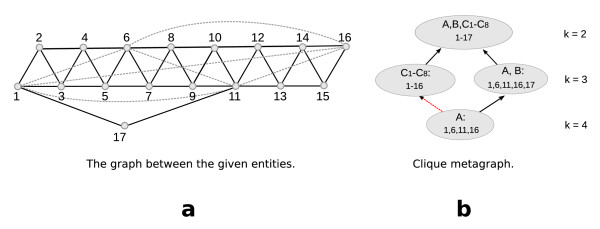
Figure 7.
(a) The example shows one maximal clique A of size 4 with A = (1, 6, 11, 16) (dashed, grey lines), and 11 maximal cliques of size 3, namely B = (1, 11, 17) and Ci = (i, i +1, i +2) for all 1 ≤ i ≤ 14. Note that A and B share two nodes with each other but at most one node with every of the Ci cliques. (b) Clique A constitutes the only 4-clique community on level 4. On level 3 we see one 3-clique community consisting of all Ci cliques and one consisting of A and B. Note that, as stated in Theorem 4, clique A is contained in only one 3-clique community. However, the set of nodes (1, 6, 11, 16) is contained in both of the corresponding 3-node clusters. The containment relation is indicated by the red, dashed arrow. Thus this graph provides an example where the containment relationship on the level of k-node clusters does not have to be hierarchic. This graph is additionally an example for a case in which the number of k-clique communities is neither monotonically increasing nor decreasing with increasing k.