Predicting continuous local structure and the effect of its substitution for secondary structure in fragment-free protein structure prediction

Abstract

Local structures predicted from protein sequences are employed extensively in every aspect of modeling and prediction of protein structure and function. For more than 50 years, they have been predicted at a low-resolution coarse-grained level (e.g. three-state secondary structure). Here, we combine a two-state classifier with real-value predictor to predict local structure in continuous representation by backbone torsion angles. The accuracy of the angles predicted by this approach is close to that derived from NMR chemical shifts. Their substitution for predicted secondary structure as restraints for ab initio structure prediction doubles the success rate. This result demonstrates the potential of predicted local structure for fragment-free tertiary-structure prediction. It further implies potentially significant benefits from employing predicted real-valued torsion angles as a replacement of or supplement to the secondary-structure prediction tools employed almost exclusively in many computational methods ranging from sequence alignment to function prediction.

Prediction of the local structure of proteins is dominated by secondary structure prediction for which the accuracy has stagnated between 77% and 80% for more than a decade (Rost, 2001; Dor and Zhou, 2007a). This stagnation contributes to the slow progress of ab-initio structure prediction that depends on predicted secondary structure to reduce the conformational space (Simons et al., 1997; Ortiz et al., 1998; Eyrich et al., 1999; Hardina et al., 2000; Fain and Levitt, 2003; Nanias et al., 2003) or guide folding pathways (Ozkan et al., 2007; DeBartolo et al., 2009). The accuracy of secondary structure prediction further significantly affects the quality of many applications including multiple sequence alignment (Zhou and Zhou, 2005), fold recognition (Fischer and Eisenberg, 1996) and prediction of structural disorder and flexibility (Schlessinger and Rost, 2005; Young et al.,1999; Radivojac et al., 2007), and function (Godzik et al., 2007). However, the effectiveness of predicted secondary structure is often limited by its coarse-grained representation of local backbone structures. Helices and strands often deviate from their ideal shapes in protein structures while the structures commonly characterized as coils do not have a definite shape. Moreover, defining secondary structure is somewhat arbitrary. The arbitrarily defined boundaries and structural flexibility limit the theoretically possible prediction accuracy to 88–90% (Rost, 2001; Kihara, 2005).

Local structures of proteins can be exactly described by their backbone torsion angles in an unambiguous way. In practice, these continuous angles were discretized because various secondary-structure types are clustered at different regions in the Ramachandran ϕ−ψ diagram (Ramachandran and Sasisekharan, 1968). Discretized angle states were employed as a replacement of, or supplement to, secondary structure for refined local-structure classifications. They were also utilized to construct simplified protein models for sampling efficiency. This development led to sequence-based methods for multi-state torsion-angle prediction (Gibrat et al., 1991; Rooman et al., 1991; Kang et al., 1993; Bystroff and Baker, 1998). Unfortunately, multi-state torsion angles are as difficult as secondary structure to predict accurately. For example, a recent study (Zimmermann and Hansmann, 2008) shows that a three-state prediction has an accuracy of 79%, the same level of accuracy of secondary structure prediction (Dor and Zhou, 2007a). Lower accuracy is reported in earlier studies with more states defined (Bystroff et al., 2000; Kuang et al., 2004). No apparent advantage of predicted multi-state torsion angles over predicted secondary structure led to few applications that actually use predicted multi-state torsion angles.

Recently, we have demonstrated that local structures of proteins can be predicted in continuous representation with reasonable accuracy. We introduced Real-SPINE (Real-value prediction of protein Structural Properties by Integrated NEural network) for a real-value prediction of ψ (Dor and Zhou, 2007b) and ϕ torsion angles (Xue et al., 2008) and subsequently improved its accuracy by guided learning and other techniques (Real-SPINE 3) (Faraggi et al., 2009). However, not all ϕ and ψ angles can be sampled by the backbone of proteins because of internal steric constraints between backbone atoms (Ramachandran and Sasisekharan, 1968). These three-dimensional physical constraints are difficult to learn by a machine learning technique with one-dimensional sequence-based information as the only input. By contrast, multi-state prediction avoids this problem by defining discrete ϕ − ψ states in sterically allowed regions only.

Here, we propose an approach that combines the advantage of discrete state classifier (avoiding sterically prohibited regions in the Ramachandran ϕ − ψ diagram) with that of real-value prediction (removing arbitrary definition of discrete states). We refer to this method as SPINE X with X denoting the combination of the two approaches. The resulting predicted angles are further refined with a conditional random field model (SPINE XI with I denoting refinement). The final predicted angles are not only substantially more accurate than multi-state classifiers for predicting discrete states but also their accuracy is close to the accuracy of the real-value angles derived from NMR chemical shifts. We further found that this new level of accuracy and real-value detail of predicted local structures brings substantial improvement in the success rate of fragment-free tertiary-structure prediction. The result has significant implication for other computational methods that have relied on discrete secondary structure prediction for characterizing unknown local structures of proteins.

Results

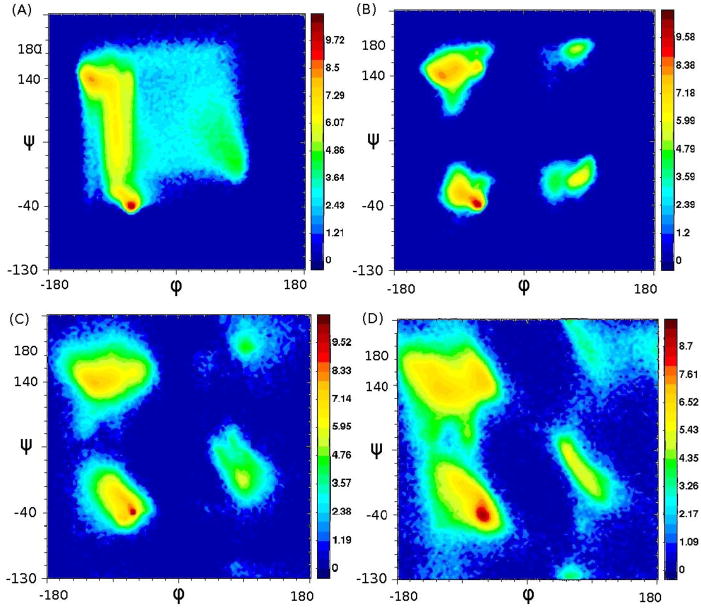
Ramachandran and his coworkers (Ramachandran and Sasisekharan, 1968) found that not all torsion angles of protein backbones are sampled by proteins because of internal steric constraints. Fig. 1d shows the statistical distribution of native angles of a database of 2640 proteins (Dor and Zhou, 2007a). The angles are distributed around preferred values, as determined by their secondary structure states, while in the rest of the ϕ−ψ plane no angles are found. These forbidden regions caused by three-dimensional physical constraints are difficult to learn by a machine learning technique with one-dimensional sequence-based information as the only input. Indeed, Fig. 1a shows that many angles predicted by a previously-developed real-value predictor (Real-SPINE 3) are in sterically forbidden regions when compared to the same diagram for native values of torsion angles (Fig. 1d). In fact, these predicted angles cover essentially every area within a square boundary.

Figure 1.

The Ramachandran plot of 10-fold cross-validated predictions of 2640 proteins by a previous real-value prediction method called Real-SPINE 3 (A), by combining a two-state classifier with real value prediction, SPINE X (B), post-refinement, SPINE XI (C), and native dihedral angles (D). The ψ axis is shifted for a clearer view of the population separation. No shift was done on the ϕ angles.

To solve this problem, we observed that both ϕ and ψ angles have a bimodal distribution as revealed from the four populated regions in Ramachandran diagram of native angles (Fig. 1d). That is, we can make an unambiguous assignment of two separate states for each angle. Following this line of reasoning, we first classified ψ (or ϕ) into two states (peak I or peak II), i.e., made a two-state prediction of the angle. The two-state prediction was followed by a prediction of the real-value deviation of the native angle from the peak. Fig. 1b indicates that this SPINE X method separates predicted torsion angles into four isolated regions as designed and eliminates angles in non-allowed regions. However, predicted angles are distributed too narrowly around predefined centers. Much wider distributions are observed in the native Ramachandran diagram (Fig. 1d). Moreover, the population distribution in the bottom right is approximately parallel to the axis ϕ (Fig. 1b), rather than to the ϕ = −ψ axis (Fig. 1d).

To further improve the accuracy of angle prediction given by SPINE X, we applied a conditional random field (CRF) model (Lafferty et al., 2001) that utilizes both ϕ^NN and ψ^NN produced by the neural networks to predict these errors (i.e., ϕ^Native − ϕ^NN and ψ^Native − ψ^NN). We employed the CRF model because a combination of two totally different methods often yields improvement in machine learning. In particular, the CRF model optimizes the conditional probability of the entire sequence, information that is not utilized as input to the neural networks. Furthermore, the CRF model takes into account the possible coupling between ϕ and ψ angles by using both angles together. The predicted errors from the CRF model are used to refine the prediction of torsion angles. As Fig. 1c shows, the ϕ − ψ diagram obtained from SPINE XI is much closer to the native angle distribution (Fig. 1d).

The improvement of the angle distribution in the Ramachandran diagram from Fig. 1a to Fig. 1c is accompanied by improvement in prediction accuracy. One can measure accuracy by Q_60°, the fraction of residues for which both predicted angles are within 60 degree from their corresponding native values (Cavalli et al., 2007). We found that Q_60° increases from 74.6% by Real-SPINE 3 (Faraggi et al., 2009) to 81.5±0.4% by SPINE X and to 82.7±0.4% by SPINE XI. That is, there is an 8% absolute (11% relative) improvement from Real-SPINE 3. By comparison, if ideal angles are used for predicted helical and strand residues and an average angle for coil residues (−25.9° for ϕ and 22.3° for ψ), Q_60° is only 61% (a separate average-coil angle value for each residue type would increase Q_60° to 64%). The large improvement can be confirmed by other measures of the accuracy. For example, Q_36°, the fraction of residues for which both predicted angles are within 36° from their corresponding native values, increases from 62% in Real-SPINE 3 to 72% in SPINE X and 74% in SPINE XI, a total of 12% absolute improvement. The mean absolute error (MAE) of the angles is defined as the average absolute difference between predicted and measured angles, e.g., for $\psi \mathit{MAE}={\sum }_{i=1}^N|{\psi }_i^{\text{pred}}-{\psi }_i^{\text{Native}}|/N$. The MAE for ψ reduces from 36.1±0.8° by a “pure” real-value prediction method (Real-SPINE 3) (Faraggi et al., 2009), to 35.2±0.6° by SPINE X, and to 33.4±0.7° by SPINE XI. This is a total of 2.7° (7%) reduction in MAE from Real-SPINE 3. The CRF refinement produces a smaller improvement in Q_60° or Q_36° than it did for the MAE because the CRF tends to make small (less than 60°) corrections to the angles. For example, Q_10°, the fraction of residues for which both predicted angles are within 10° from their corresponding native values, increases from 29% in SPINE X to 34% in SPINE XI, a 5% absolute improvement. Significant improvement from Real-SPINE 3 to SPINE XI (11% relative improvement in Q_60°) confirms the advantage of combing a two-state classifier with a real-value predictor followed by subsequent refinement.

We further found that the accuracy of angle prediction strongly depends on the secondary structure types. The prediction accuracy is the highest for helical residues. Q_60° = 95.2%, 89.4%, and 64.7% for helical, strand, and coil residues, respectively. These values are 0.1%, 1.0%, and 2.6% improvement from the respective values prior to the CRF refinement. Torsion angles of coil residues are most difficult to predict because of their irregular structures. Thus, predicted secondary structure types can be used as a coarse-grained estimation of the accuracy of angle prediction. The proposed SPINE XI method can be compared to multi-state predictors by mapping real-value prediction onto pre-defined states. Kuang et al. (Kuang et al., 2004) and Bystroff et al. (Bystroff et al., 2000) followed a definition that divides the ϕ−ψ plane into 81 square grids and predicted grid-defined four states (A, B, G, and E) (Oliva et al., 1997) by neural networks and hidden Markov model, respectively. We achieved 84% correct identification, compared to 74% by Bystroff et al. (Bystroff et al., 2000) and 77% by Kuang et al. (Kuang et al., 2004). Zimmermann and Hansmann (Zimmermann and Hansmann, 2008), on the other hand, predicted 16-state 5-residue building blocks of 8 consecutive torsion angles (de Brevern et al., 2000). They achieved 61% for correctly predicting 16 states and 79% for predicting three secondary-structure states. By comparison, we obtained 66% and 81%, respectively. This 5% or 2% improvement is made despite that both SPINE X and XI were trained to predict the angles of a single residue at a time. Thus, multi-state assignment based on real-value prediction is more accurate than the methods dedicated to predict them whether or not they are defined in single residue, in a fragment of several residues, in a small number of states, or in a large number of states.

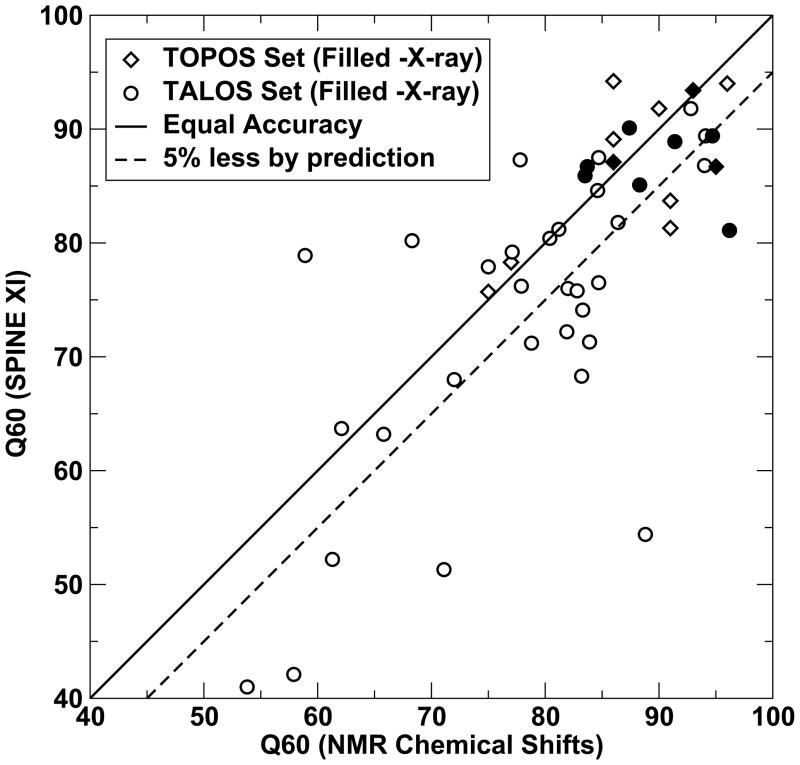
How accurate are real value torsion angles predicted by SPINE XI relative to the values obtained from NMR chemical shifts? Recently, Cavalli et al. (Cavalli et al., 2007) developed and used a method called TOPOS, which is similar to TALOS (Cornilescu et al., 1999), to determine the backbone torsion angles most compatible with the experimental chemical shifts in a database of three-residue fragments. They applied TOPOS to 11 proteins and the results are compared to SPINE XI in Fig. 2 (also Table 1). The average accuracy is 88% by TOPOS (Cavalli et al., 2007) and 86.9% by SPINE XI.

Figure 2.

The accuracy of torsion angles obtained from NMR chemical shifts by programs TOPOS (11 proteins) and TALOS (37 proteins) is compared to that given by SPINEXI. Accuracy is measured by Q_60°, the fraction of residues for which both ϕ and ψ angles are less than 60° away from their respective native values. SPINE XI makes equally or more accurate prediction for 20 proteins (42%). NMR-derived angles are only slightly more accurate than SPINE XI for an additional 10 proteins (less than 5% difference) (dashed line).

Table 1.

The accuracy measured by Q_60° for torsion angles obtained by TOPOS based on NMR chemical shifts (Cavalli et al., 2007) and predicted by SPINE XI for 11 proteins.

Protein	PDB IDa	Lb	%α/β/coilc	TOPOS(%)d	SPINE XI(%)
Bet v 4	1h4b	84	64/4/32	96	94.0
Calbindin	3icb(X)	74	60/0/40	95	86.7
FF domain	1uzc	54	77/0/23	86	94.2
HPr	1poh(X)	85	37/29/34	86	87.1
Sda	1pv0	46	60/0/40	86	89.1
Δ27-GG	1sa8	106	0/65/35	77	78.3
TM1442	1sbo	110	44/20/36	90	91.8
Ubiquitin	1ubq(X)	76	25/32/43	93	93.4
MrR5	1yvc	70	0/51/49	75	75.7
PhS018	2glw	92	21/50/29	91	83.7
Sen15	2gw6	123	32/29/39	91	81.3
Ave.			38/26/36	88	86.9

^aProtein Data Bank Identification Number. The method used to solve the structure is NMR unless it is specifically indicated as (X) for X-ray.

^bNumber of residues.

^cFraction of helical, strands, and coil residues (Cavalli et al., 2007).

^dFrom Ref. (Cavalli et al., 2007).

To further confirm the result described above, we obtained a set of proteins with both the chemical shift data and PDB structures from the BioMagResBank database (Doreleijers et al., 2003) (http://restraintsgrid.bmrb.wisc.edu/NRG/MRGridServlet). We removed the proteins whose sequences from the chemical shift data mismatch with the corresponding sequences from the PDB structures. This led to a total of 37 proteins. For some proteins with multiple PDB entries, we used the X-ray crystal structure with the highest resolution. This set of proteins is a challenging set because the average fraction of coil residues (43%) is significantly higher than either the above 11-protein set (36%) or the training/test benchmark of 2640 proteins (39%) (Dor and Zhou, 2007a) (See methods). Nevertheless, the accuracy given by TALOS (Cornilescu et al., 1999) based on experimental chemical shifts (79.8%) is only 4% higher than the proposed method (75.5%), a successful result considering that our method is trained entirely on X-ray structures (Fig. 2 and Table 2). A smaller difference (2.6%) in accuracy (89.3% by TALOS and 86.7% by SPINE XI) is observed when X-ray crystal structures (a total of 7) are used for obtaining native torsion angles as shown in Fig. 2 and Table 2.

Table 2.

The accuracy measured by Q_60° for torsion angles obtained by TALOS based on NMR chemical shifts (Cornilescu et al., 1999) and predicted by SPINE XI for 37 proteins.

#bmra	PDBb	Lc	%α/β/coild	TALOS(%)e	SPINE XI(%)
10118	2exd	72	0/40/60	81.9	72.2
11022	2rng	76	28/15/57	71.1	51.3
11036	2ro1	186	36/2/62	61.3	52.2
11055	1jyr(X)	94	17/25/58	88.3	85.1
15125	2jns	85	46/0/54	94.1	89.4
15177	1r1v(X)	94	65/10/25	94.7	89.4
15247	2v9h	151	32/35/33	94.0	86.8
15283	1igd(X)	53	25/42/33	96.2	81.1
15393	2jss	190	57/0/43	62.1	63.7
15439	2juc	52	64/0/36	78.8	71.2
15444	2ckx(X	81	70/0/30	91.4	88.9
15469	2jzd	125	44/15/41	88.8	54.4
15528	2jwn	122	23/26/51	77.9	76.2
15534	2juj	54	61/0/39	83.3	74.1
15579	2jy0	25	56/0/44	72.0	68.0
15622	2job	90	43/30/27	58.9	78.9
15677	2k1e	101	68/0/32	68.3	80.2
15953	3e2b(X)	85	34/43/23	83.5	85.9
287	1ner	63	53/0/47	77.8	87.3
4090	2ezi	72	61/0/39	84.7	87.5
4224	2myo	114	47/0/54	65.8	63.2
4333	2gf5	97	74/0/26	92.8	91.8
4540	1nla	50	62/0/38	82.0	76.0
5141	1t4z	87	35/23/42	83.9	71.3
5211	1d4t(X)	111	17/29/54	87.4	90.1
5596	1n91	101	22/30/48	83.2	68.3
5824	1v2z(X)	98	81/0/19	83.7	86.7
6085	1s6w	19	0/29/71	57.9	42.1
6127	1se7	80	58/0/42	81.2	81.2
6128	1se9	99	15/29/56	82.8	75.8
6147	1y6d	112	79/0/21	80.4	80.4
6324	1x9a	85	39/17/44	84.7	76.5
6392	1o7c	96	18/24/58	77.1	79.2
6432	1wvk	78	17/7/76	53.8	41.0
6553	1yza	104	63/0/37	75.0	77.9
6560	1yyx	104	76/0/24	84.6	84.6
6571	2ae9	66	65/0/35	86.4	81.8
Ave (X ray)			44/21/35	89.3	86.7
Ave (All)			45/13/43	79.8	75.5

^abmr identification number.

^bProtein Data Bank Identification Number. The method used to solve the structure is NMR unless it is specifically indicated as (X) for X-ray.

^cNumber of residues predicted by TALOS.

^dFraction of helical, strands, and coil residues.

^eTALOS program was downloaded from http://spin.niddk.nih.gov/NMRPipe/talos/.

The above comparison in Q_60° does not mean that the accuracy of our predicted local structures is close to the accuracy of local structural information contained in NMR chemical shifts. Both TOPOS and TALOS are only approximate methods that derive torsion angles from NMR chemical shifts. In fact, NMR chemical shifts, rather than the torsion angles derived from NMR chemical shifts, are directly employed as restraints in structure prediction (Cavalli et al., 2007; Gong et al., 2007; Shen et al., 2008; Wishart et al., 2008; Montalvao et al., 2008; Robustelli et al., 2008; Shen et al., 2009). The purpose of the comparison made here is only to illustrate the new level of accuracy achieved by SPINE XI in real-value torsion-angle prediction.

It is of interest to know the relative contribution of various inputs employed in neural networks to the accuracy of torsion angle prediction. There are three key components for neural-network inputs: sequence profiles, representative residue properties, and predicted one-dimensional structure properties (secondary structure and solvent-accessible surface area) [See methods]. Table 3 shows the effect of different input combinations on Q_36° for ϕ and ψ, respectively. It is clear that sequence profile or predicted one-dimensional structure properties alone achieve similar accuracy while the combination of the three inputs further improves the accuracy by an additional 1–2% for ϕ and 3% for ψ. The improvement, although small, reaffirms the usefulness of combined inputs. In the method described above, peak prediction and the deviation from the peak are predicted separately. We also tested the idea of including predicted peaks as an input for predicting peak deviations. We did not observe significant improvement in either Q_60° or Q_36°. This suggests that predicting the deviation from the peak has utilized the peak location implicitly contained in same neural-network inputs employed for peak prediction.

Table 3.

The accuracy (Q_36°) of SPINE X given by different combinations of inputs (Sequence profiles, representative residue properties, and predicted structural properties including secondary structure and solvent accessible surface area) employed in neural networks.^a

Seq. Profile	Properties	Predicted SP	ϕ	ψ
X			83%	76%
	X		79%	66%
		X	84%	76%
X	X		84%	78%
X		X	84.5%	78.5%
	X	X	84.5%	78%
X	X	X	85%	79%

^aThis result is from testing on one fold.

To illustrate the usefulness of the improved real-value prediction relative to that of secondary structure prediction, we predicted protein structures via restraining local structure represented by three predicted secondary-structure states and by continuous representation of predicted torsion angles. A coarse-grained energy function is employed in the absence of any native information (i.e. no protein fragments or templates). Here, we examine whether or not the restraints based on predicted torsion angles or predicted secondary structure can guide a coarse-grained energy function to the right structural folds (Root-mean-squared distance, RMSD, <6Å) (Reva et al., 1998) within top predicted structures – the critically important first step of protein structure prediction (see Methods). We defined a successful prediction of a structural fold if the best structure in top 15 predicted structures has an RMSD of 6Å or less.

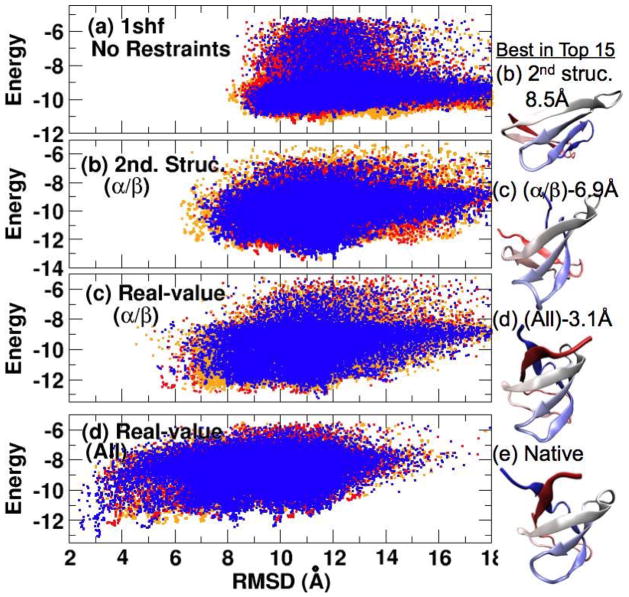
Fig. 3 displays one typical example of the effects of different angle restraints on conformational sampling and structure prediction. The energy values of sampled structures for protein 1shf are shown as a function of their RMSD values with various restraints as labeled from top to bottom in Fig. 3. Without any restraints, the RMSD values of all sampled structures are greater than 8Å. Adding the restraints based on ideal secondary structure (only predicted strand residues for this protein) improves the best-sampled structure to near 6Å RMSD. However, the best structure in top 15 predicted structures (Fig. 3 Structure b) continues to have a high RMSD value of 8.5Å. Restraining around real values of predicted torsion angles for predicted strand residues leads to β strands of the best structure in top 15 that are non-ideally shaped but more native-like (Fig. 3 Structure c). The RMSD value of the best sampled structure and that of the best structure in top 15 reduce to 4.5Å and 6.9Å, respectively. It is clear that the predicted deviation from an ideal β strand conformation leads to significantly more effective conformational sampling of near native structures. Adding the predicted restraints of predicted coil residues further decreases the RMSD values to 2.5Å for the best sampled structure and to 3.1Å for the best structure in top 15. This best structure in top 15 has the lowest energy. That is, the structure information contained in coil residues leads to the correct prediction of the structure for 1shf.

Figure 3.

The effects of various restraints on conformational sampling of 1shf. The energy of all sampled conformations as a function of their RMSD values from the native structure. From top to bottom, conformations are sampled without any restraints (a), with predicted secondary-structure restraints (i.e. restraining around the ideal angles of predicted helical and/or strand residues) (b), with restraints around predicted real-value torsion angles of predicted helical and/or strand residues only (c), and with restraints around predicted torsion angles for all residues (d). The corresponding best structures in top 15 for (b) to (d) are shown in the right panel and the native structure is shown in (e).

Table 4 summarizes the results for a benchmark of 16 proteins (Bradley et al., 2005). Adding predicted secondary-structure restraints to a coarse-grained energy increases the number of successful prediction from 2 to 6 out of 16 proteins and the median RMSD value for the best in top 15 decreases from 9Å to 6Å. This significant change results from highly accurate secondary structure prediction for this set of benchmark proteins (an average Q₃ of 85%). More importantly, this level of success can be further significantly improved by simply replacing ideal angles of predicted helical and strand residues with predicted real values of the same restrained residues. The median value of the best in top 15 structures decreases by an additional 1Å (from 6Å to 5Å) and the number of successful predictions increases by another 67% (from 6 to 10). Thus, predicting torsion angles in real values makes more powerful restraints than predicting secondary structure in ideal representation even before the predicted angles of coil residues are put into use.

Table 4.

The root-mean-squared distance (RMSD) from the native structure of the best structure in top five clusters of three independent runs (top 15) by an energy function only, with restraints around ideal angles of predicted helical and strand residues (secondary structure restraints), around predicted real-value angles of predicted helical and strand residues, and around predicted real-value angles of all residues.

PDB IDa	Lb	α/β/coil (%)c	Q60° (%)d	Q3 (%)e	Best RMSD in Top 15 in Å
					No Res.f	Ideal α&βg	Real α&βh	Alli
1b72	49	71/0/29	66.6	67.3	4.9	5.3	5.1	6.5
1shf	59	0/42/58	86.0	79.7	9.1	8.5	6.9	3.1
1tif	59	24/37/39	89.5	84.7	8.5	6.2	4.5	4.2 (3.4j)
2reb	60	62/22/16	91.4	85.0	6.6	3.2	5.6	3.2
1r69	61	71/0/29	93.2	96.7	6.7	9.0	6.2	2.0
1csp	67	0/55/45	86.2	77.6	10.4	7.3	6.1	4.9
1di2	69	42/33/25	92.5	95.7	11.6	3.8	6.5	3.2
1n0u	69	45/28/27	98.5	87.0	9.4	4.1	4.2	4.1
1mla	70	37/37/26	91.2	90.0	8.0	3.0	3.3	4.4
1af7	72	71/0/29	95.7	97.2	5.8	6.1	4.9	3.1
1ogw	72	26/32/42	90.0	79.2	8.0	6.8	6.5	6.0
1dcj	73	36/32/32	90.1	91.8	8.9	4.2	4.1	3.2
1dtj	74	41/27/68	83.3	83.8	10.2	6.3	5.2	5.1
1o2f	77	48/29/23	84.0	81.8	9.5	6.6	5.7	9.7
1mky	81	35/25/40	91.1	86.4	11.9	7.0	4.5	8.0 (5.2j)
1tig	88	39/35/26	82.6	75.0	10.7	11.7	10.5	10.6
Median:		40/27/33k	88.2k	84.9k	9.0	6.3	5.4	4.3
Success Rate (RMSD<6Å)l:					2/16	6/16	10/16	12/16

^aProtein Data Bank Identification Number (a dataset of Ref. (Bradley et al., 2005)).

^bChain length (Bradley et al., 2005).

^cFractions of native helical, strand and coil residues.

^dFraction of residues for which predicted angles are within 60° from their native values for both ϕ and ψ angles.

^eThe accuracy of secondary structure prediction by an improved version of SPINE (Dor and Zhou, 2007a; Faraggi et al., 2009). The best structure (in RMSD) in top five clusters of three independent runs (top 15)

^fwithout torsion angle restraints (DFIRE plus hydrogen bonding only).

^gThe energy function plus restraints around ideal angles of predicted helices and strands.

^hThe energy function plus restraints on predicted real values of torsion angles of predicted helical and strand residues only.

ⁱThe energy function plus restraints on all residues.

^jA native cis-conformation is assigned to Pro 54 in 1tif and Pro 394 (ω = 0°) in 1mky.

^kAverage.

^lThe success rate: the number of proteins having a correct structural topology (RMSD<6Å) ranked within top 15.

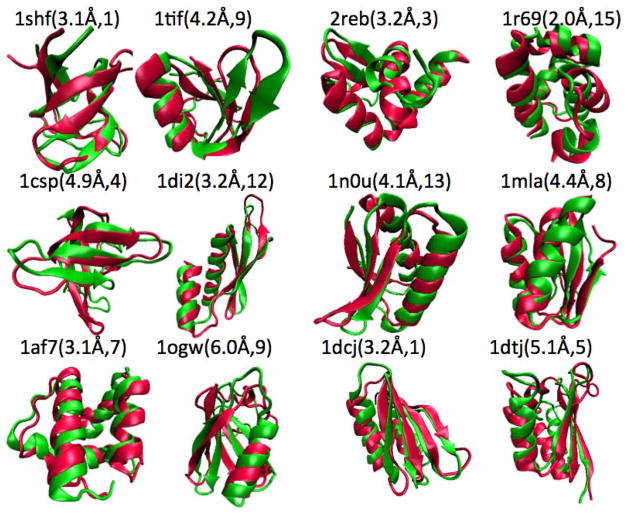
Adding restraints on coil residues further improves the overall accuracy of structure prediction. As shown in Table 4, additional restraints on predicted coil residues increase the number of successful predictions by another 20% from 10 to 12 and decrease the median RMSD value by an additional 1Å from 5Å to 4Å. The improvement is observed for the majority of proteins (11 out of 16). Thus, employing the real-value prediction doubles the success rate (from 6 to 12) over employing the predicted secondary structure, by taking into account non-ideal helical and strand conformations and the structures of coil residues. As shown in Fig. 4, the predicted structures reproduce the overall structures of the 12 native structures very well.

Figure 4.

Comparison between predicted structure (best in top 15, in Green) and native structure (in Red) for 12 proteins as labeled, along with their ranks.

There are only four exceptions to the improvement with additional restraints on coil residues. A large increase in the RMSD value of the best structure in top 15 is observed for three proteins: 1b72, 1o2f, and 1mky. While restraining all residues for these three proteins is not successful, restraining only predicted helical and sheet residues successfully predicts their respective structural folds within top 15 structures. The RMSD values of the best structures in top 15 for the three proteins are 6.5Å, 9.7Å, and 8.0Å, respectively, with coil restraints, and 5.1Å, 5.7Å, and 4.5Å, respectively, without coil restraints. This suggests a strategy that combines top candidates predicted with and without coil restraints for further all-atom refinements. Such a simple combination will lead to correct structural folds within top 30 structures for 15 out of 16 proteins. This result also highlights that there is room for further improvement in torsion angle prediction of coil residues.

The above improvement is based on RMSD values. It is of interest to know if other criteria (Sippl, 1982; Siew et al., 2000; Zhang and Skolnick, 2004a) for measuring the accuracy of structures predicted would reveal similar improvement as well. Here we apply the recently developed TM-Score (Template-modeling score) that was designed to be independent of protein sizes. A TM-Score is 1 for perfect match and below 0.2 between two random structures. The median TM-score for the best in top 15 is 0.30, 0.38, 0.45, and 0.54 as we change from no angle restraints, ideal helical and strand restraints, real-value helical and strand restraints to angle restraints on all residues. That is, there is a 42% improvement in structural quality from secondary structure to real-value torsion-angle restraints. This 42% improvement is higher than 32% reduction in RMSD from 6.3Å to 4.3Å. Similar result (38% improvement from secondary structure to real-value torsion-angle restraints) is obtained if the MaxSub score is employed (Siew et al., 2000).

This work predicts ϕ and ψ torsion angles only and all ω torsion angles are fixed to 180° in structure prediction. However, there is a small population of Pro residues that adopt the cis conformation (ω = 0°). For the 16-protein benchmark, this is true for Pro 394 in 1mky, Pro 54 in 1tif, and Pro 20 and Pro 72 in 1dcj. To test the effect of the cis conformation, we fixed ω to 0° for Pro 394 in 1mky and Pro 54 in 1tif. This leads to a significant reduction of the RMSD value of the best structure in top 15 prediction for both 1mky (from 8.0 to 5.2Å) and 1tif (from 4.2 to 3.4Å). Thus, a large improvement of one torsion angle can impact significantly the accuracy of predicted structures. On the other hand, incorrect ω angles do not prohibit the ability to predict correct structural folds for 1tif (4.2Å RMSD, ranked 9) and 1dcj (3.2Å RMSD, ranked 1). That is, the error of a few incorrect angles can be corrected by the adjustment of other torsion angles. This explains the observed success of imperfectly predicted torsion angle restraints for structure prediction. In principle, one could also develop a method to predict ω angles as well. However, the rare events of cis conformations are more difficult to predict because they mostly result from nonlocal interactions. We will incorporate cis conformations during conformational sampling in future studies.

Finally, we are unable to locate an obvious reason for the inability to predict correct structural folds for 1tig within top 15 with or without restraints. Nevertheless, the best structure sampled with restraints (6.2Å RMSD) in all sampled structures is substantially more accurate than the best structure in the absence of any restraints (8.9Å RMSD). It is quite possible that the restraints for this protein are unable to correct or compensate for the error contained in the two-term coarse-grained energy function.

Further Discussion and Concluding Remarks

This paper demonstrates a new level of accuracy achieved for predicted local structures either in exact description by real-value torsion angles or by mapping to multiple predefined states. The application to structure prediction reveals that predicted real-value torsion angles are substantially more effective than predicted secondary structure as local structural restraints for tertiary structure prediction, a technique commonly used in structure prediction methods including ROSETTA (Simons et al., 1997) and TASSER (Zhang and Skolnick, 2004b). These results highlight the power of the newly proposed approach for local structure prediction: defining only states that have clear boundaries from other states and further refining the states by real-value assignments within each one. SPINE XI is available as a server at http://sparks.informatics.iupui.edu.

More importantly, almost all sequence-based prediction methods utilized predicted secondary structures. Examples are protein domain divisions (Cheng et al., 2006; Gewehr and Zimmer, 2006; Tress et al., 2007), dynamical properties of structures (residue fluctuation or temperature B-factor (Schlessinger and Rost, 2005; Yuan et al., 2005), conformationally variable or switching regions (Yoon and Welsh, 2005; Young et al., 1999; Gross, 2000; Boden et al., 2006; Kuznetsov, 2008), intrinsic disorder (Ferron et al., 2006; Dosztanyi et al., 2007; Bourhis et al., 2007; Radivo jac et al., 2007)), and function prediction methods (See recent reviews (Godzik et al., 2007; Yang, 2004; Lopez et al., 2007)). In fact, Libley et al. showed that predicted secondary structures make the largest contribution to function prediction (Lobley et al., 2007). Several initial applications of torsion angles predicted by earlier methods appear to be promising for improving fold recognition (Karchin et al., 2003; Wu and Zhang, 2008; Zhang et al., 2008) and sequence alignment (Huang and Bystroff, 2006). Because our newly predicted torsion angles are more accurate even when mapped onto a few coarse-grained states, a simple update or addition of real-value local structure prediction will likely improve those computational methods relying on the accuracy of secondary structure prediction.

Lastly, it is worth mentioning an alternative approach. We have employed predicted angles as restraints for structure prediction. Another possibility is to predict preference of torsion angles given sequence and secondary structure information during conformational sampling using a probabilistic model (Boomsma et al., 2008; Zhao et al., 2008). Both continuous sampling approaches provide an alternative to discrete fragment-based sampling.

Method

A. Torsion-angle predictions by neural networks (SPINE X)

Torsion angles were first predicted by a neural-network based method with sequence as its only input. The proposed method combines the advantage of multi-state prediction (avoiding sterically prohibited regions) and that of real-value prediction (Xue et al., 2008; Faraggi et al., 2009) (removing arbitrary definition of states). This is done by first designating the two most popular ϕ and ψ angles as the peaks in their distribution. Then, two separate neural networks are employed. The first neural network is used for predicting the peak that ϕ or ψ is closest to. The second neural network is used for predicting the angle deviation from the peak. The results from the two networks are combined to yield the real values of torsion angles. ϕ and ψ angles are predicted separately. The architecture of neural networks can be found in Fig. 5. The dataset (2640 non-redundant high-resolution protein structures with 25% sequence identity cutoff), training and testing (ten-fold cross validation) used in this work are the same as those published previously (Xue et al., 2008; Faraggi et al., 2009). More specifically, this dataset was built on the protein sequence culling server PISCES (Dunbrack, 2006) with sequence identity less than 25% and X-ray resolution better than 3Å. The chains with unknown structure regions were removed. The final dataset contains a total of 591,797 residues.

Figure 5.

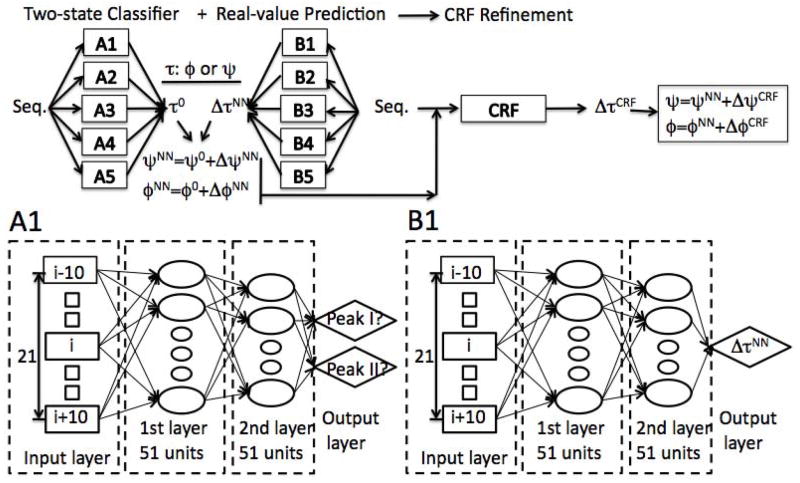
Network architecture for real-value prediction of backbone torsion angles (SPINE XI). Two sets of neural networks are constructed for predicting angle peaks (Peak I or Peak II) by a two-state classifier (A1–A5) and the deviation from the peak by a real-value predictor (B1–B5). Both predictions result from a consensus of five independent predictions. Each predictor (A1,..A5,B1,…B5) has two hidden layers. Angles predicted by neural networks are further refined by the conditional random field (CRF) model.

Input for the neural networks

We used a window size of 21 amino acids with ten residues to either side of the central residue whose angles we wish to predict. Vacant locations in the windows around residues near the terminals of the protein are explicitly excluded from the machine learning by limiting the size of the window for those regions. Each amino acid residue has 31 input features. They include the seven representative amino acid properties (steric parameter, hydrophobicity, volume, polarizability, isoelectric point, helix probability and sheet probability) (Dor and Zhou, 2007a; Meiler et al., 2001), 20 values from the Position Specific Scoring Matrix (PSSM) obtained from PSI-BLAST (Altschul et al., 1997) with three iterations of searching against a non-redundant sequence database, a real-value solvent accessibility prediction (Faraggi et al., 2009), and predicted three-state secondary-structure probabilities (3 values). The latter is obtained from an improved version of SPINE (Dor and Zhou, 2007a) based on guided learning and predicted torsion angles (Faraggi et al., 2009) (details will be published elsewhere).

Network architecture

As shown in Fig. 5, we employ two separate neural networks: one makes a two-state prediction (Peak I and Peak II) and the other predicts the deviation from the peak. The two-state prediction has two output neurons that represent the absolute distance from peak I and II, respectively. A smaller distance indicates the peak location. The network for peak deviation has one output neuron that predicts the difference between the angle and its peak location of native-angle distribution. Both networks consist of two hidden layers with a bipolar activation function [tanh(αx) with α = 0.2] (Faraggi et al., 2009). Each hidden layer contains 51 neurons. For ϕ, peaks I and II are located at −62° and 57°, respectively. For ψ, they are located at −40° and 140°, respectively. The final predicted real-value angle is the location of the predicted peak (one of the four angle pairs above) plus the predicted deviation. ϕ and ψ angles are predicted separately. Each predicted angle is a consensus prediction over five predictions independently trained by different random initial weights. This is done first by a consensus vote on the peak assignment and then by averaging the predicted deviations from the peaks over the five runs. The final predicted angles are the sum of the consensus-peak position and the averaged deviation from the peak. The accuracy of peak prediction is 96.3% for ϕ and 85.9% for ψ.

Algorithm

ψ angles are shifted by 50° such that the two peaks are situated approximately symmetrically about 0°. ϕ angles are not shifted. Neural network weights are trained by the back propagation algorithm (Rumelhart et al., 1986) with guiding factors designed to satisfy the intuitive condition that for most residues, the contribution of a residue to the structural properties of another residue is smaller for greater separation in the protein-sequence distance between the two residues (Faraggi et al., 2009). The learning rate and momentum are set as 0.01 and 0.4, respectively. The initial weights are randomly selected in the range (−0.5, 0.5) and all inputs to the neural networks are normalized in the range of (−1, 1). The weights training is tested with a 10 fold cross validation on the database of 2640 proteins with sequence identity less than 25% between them and X-ray resolution better than 3Å(Zhou and Zhou, 2004). The dataset is divided randomly into 10 groups with 264 proteins each. Each time, nine groups are used for training and one group is used for independent testing. This procedure is repeated 10 times and the prediction accuracies is averaged over the ten folds. In addition, 5% of the training set is excluded from training and used solely as an independent convergence test to avoid possible over-training (overfitting protection). The final predicted ϕ and ψ angles are labeled as ϕ^NN and ψ^NN, respectively.

B. Torsion-angle refinement by conditional random field models (SPINE XI)

The real values of both ϕ and ψ torsion angles predicted by SPINE X are used as an input to the conditional random field model (Lafferty et al., 2001) to predict the errors of those predicted angles. A CRF model (Lafferty et al., 2001), like a statistical hidden Markov model (HMM) (Baum and Petrie, 1966), is an undirected graphical (random fields) model. Unlike HMM, it directly computes the distribution of a to-be-predicted variable conditioned on known observations. CRF models can contain any number of feature functions and have been recently applied to protein fold recognition (Liu et al., 2006) and conformational sampling (Zhao et al., 2008). In our case, we used it to predict the errors in neural-network predicted angles (Δτ = τ−τ^NN with τ either ϕ or ψ) conditioned on given observations such as residue type or predicted secondary structure or their combination. These errors are employed to refine the predicted angles.

State-dependent angles

One innovative implementation of the CRF model in this work is to weight observations according to their predictive power for Δτ (see below). We used 60 states to characterize different combinations of 20 amino-acid residue types and predicted three-state secondary structures. The state-dependent angle (T_m(X), m = 1, 60) is approximated as a linear combination of predicted angles and corresponding position specific scoring matrix from PSI-BLAST (P) (Altschul et al., 1997). That is, $T_m(A_i=A_m,S_i=S_m)={\sum }_{j=1}^{20}{c}_j^m{P}_{ij}+c_{21}^m{\phi }_i^{NN}+c_{22}^m{\psi }_i^{NN}$ for a given residue i whose amino-acid type A_i is A_m and predicted secondary structure S_i is S_m. Here, the coefficients $c_j^m$ are obtained by maximizing the number of residues with |T_m(A_i= A_m, S_i= S_m)−τ_i |<36°, where τ_i is the native value of either ϕ_i or ψ_i in training. Note that we optimized the coefficients $c_j^m$ separately for ϕ and ψ.

CRF model

In the CRF model, the conditional probability of a finite set of Δτ states is defined by $P(\mathrm{\Delta }\tau \mid X)=exp\left[{\sum }_{i=1}^{N}F(\mathrm{\Delta }\tau ,X,i)]\right]/Z(X)$ with the normalization factor $Z(X)={\sum }_{l=1}^{L}exp\left[{\sum }_{i=1}^{N}F(\mathrm{\Delta }\tau ,X,i)]\right]$ for N sequentially-linked amino-acid residues and L Δτ states. Here, the function F(Δτ, X, i) is given by

$$F(\mathrm{\Delta }\tau ,X,i)=\sum _j{\lambda }_j{t}_j(\mathrm{\Delta }{\tau }_{i-1},\mathrm{\Delta }{\tau }_i,X_i)+\sum _k{\mu }_k{s}_k(\mathrm{\Delta }{\tau }_i,X_{i+l(k)})w_i(X)$$ (1)

where t_j (Δτ_i−1,Δτ_i, X_i) is a transition feature function of the entire observation sequence and Δτ at positions i and i − 1, s_k (Δτ_i, X_i+l(k)) is a state feature function of Δτ at position i and the observation sequence at position i + l(k), $w_i(X)=T_m(A_i=A_m,S_i=S_m)-{\tau }_i^{NN}$ is the weight for the observation sequence obtained above, l(k) is an index for a sliding window around i (from i − 10 to i + 10), and λ_j and μ_k are parameters to be optimized based on training data. Here, the summation over j is over all 60 observations and 11 Δτ states with regions that are separated by the boundaries at ±2°, ±8°, ±18°, ±32°, ±50° and ±180°. t_j(Δτ_i−1,Δτ_i, X_i) is a delta function. For example, when j corresponds to Δτ₁ at i − 1, Δτ₂ at position i, and X = [A_j][S_j] at position i, t_j (Δτ_i−1,Δτ_i, X_i) is nonzero, or 1, only if Δτ_i−1 = Δτ₁, Δτ_i = Δτ₂, A_i = A_j and S_i = S_j. The state feature function s_k (Δτ_i, X_i+l(k)) includes not only amino-acid type and secondary structure at position i but also its neighboring residues (a window size of 21 residues is employed). That is, the summation over k is over 60 observations, 11 Δτ states, and a 21-residue window. It should also be noted that w_i(X), depending on observations only, has only 60 values corresponding to 60 observations. When k corresponds to Δτ₂ at position i and observation X = [A_k][S_k] at position i + 2, s_k (Δτ_i, X_i+l(k)) is also a delta function which is nonzero, or 1, only if Δτ_i = Δτ₂, A_i+2 = A_k and S_i+2 = S_k.

Solving for λ_j and μ_k parameters

The CRF model trains its parameters by maximizing the conditional log-likelihood L of the data:

$$L(\lambda ,\mu )=lnP(\mathrm{\Delta }\tau \mid X)=\sum _{i=1}^{N}F(\mathrm{\Delta }\tau ,X,i)-lnZ(X)-\sum _j{\lambda }_j^2/2{\sigma }^2-\sum _k{\mu }_k^2/2{\sigma }^2$$ (2)

where the last two terms are employed to regularize the variation of model parameters, to avoid over-fitting we set σ² = 50 after a few trials. This equation is solved by a slightly modified Powell method for function maximization (Press et al., 1992). The optimization function is convex and guarantees a global minimum.

Predicting Δτ

Once λ_j and μ_k parameters are known, one can efficiently calculate the expected Δτ value via defining “forward” and “backward” vectors and using a simple dynamic programming technique (Liu et al., 2006). The final predicted angles are calculated from τ^NN+ Δτ.

Training and Testing

We employed the same 10-fold cross validation technique to estimate the accuracy of the predictions as for ϕ^NN and ψ^NN.

C. Structure prediction with torsion angle restraints

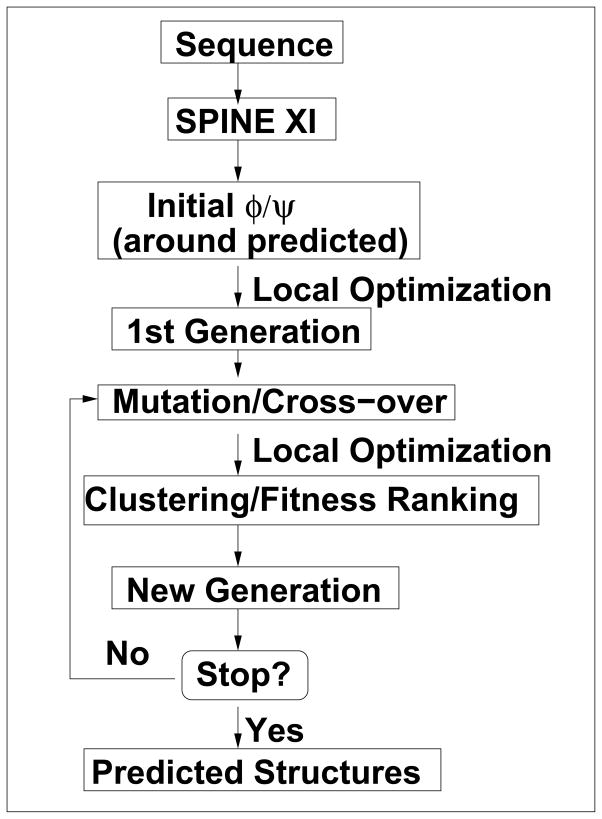
Proteins are represented by a backbone-only model. In addition to flexible torsion angle restraints, we employed an energy function made of two terms: a statistical energy for C_α and C_β atoms based on the distance-scaled finite ideal gas reference state (DFIRE) (Zhou and Zhou, 2002; Yang and Zhou, 2008b) and a geometric-based hydrogen-bonding term between main-chain amine hydrogen and oxygen atoms. Relative weights of the energetic terms were determined by trial and error. A genetic algorithm with local optimization and clustering techniques (Yang and Zhou, 2008a) was used to search the global energy minimum with (1) the energy function only, (2) the energy function with restraints around ideal angles of predicted secondary structure (helices and strands) by an improved version of SPINE (Dor and Zhou, 2007a; Faraggi et al., 2009), (3) the energy function with 14 restraints around predicted real values of the torsion angles of predicted helical and strand residues, and (4) the energy function with predicted real-value angle restraints for all residues. Ideal angles of helical residues are −57° for ϕ and −45° for ψ and that of strand residues are −129° for ϕ and 124° for ψ (Park and Levitt, 1996). Note that protein structures are predicted without employing fragments or templates of known structures. This fragment free method is described in detail below and its flow chart is shown in Fig. 6.

Figure 6.

The flow chart for the method used for fragment-free protein-tertiary-structure prediction. Details for the first part of the method, obtaining SPINE XI, are given in Fig. 5.

Protein-specific torsion restraints ( $E_I^{\phi }$ and $E_I^{\psi }$)

We restrained the torsion angles according to the neural network predictions by adding two terms to the energy function corresponding to ϕ and ψ. These two terms are given by the following equation:

$$E_I^{\tau }=\{\begin{array}{cc}0,& \mathrm{\Delta }\tau \le \mathrm{\Delta }{\tau }_{A_I,S_I}^0,\\ K{(\mathrm{\Delta }\tau /\mathrm{\Delta }{\tau }_{A_I,S_I}^0-1)}^2,& \mathrm{\Delta }{\tau }_{A_I,S_I}^0<\mathrm{\Delta }\tau \le 2\mathrm{\Delta }{\tau }_{A_I,S_I}^0,\\ K,& \mathrm{\Delta }\tau >2\mathrm{\Delta }{\tau }_{A_I,S_I}^0,\end{array}$$ (3)

where τ can be either the ϕ or ψ angle, $\mathrm{\Delta }\tau (=\mid {\tau }_I-{\tau }_I^{\mathit{pred}}\mid )$ is the absolute deviation of the τ_I angle for a given residue I from the corresponding predicted angle ( ${\tau }_I^{\mathit{pred}}$), $\mathrm{\Delta }{\tau }_{A_I,S_I}^0$ is a pre-defined, allowed angle deviation that depends on the residue type (A_I) and predicted secondary structure (S_I) for residue I, and K is a weight parameter. Δτ is evaluated with the consideration of angle periodicity (e.g., the difference between −180° and 180° is 0°, not 360°). We set K to 100 after a few trials. Predefined 60 values of $\mathrm{\Delta }{\tau }_{A_I,S_I}^0$ are obtained from a statistical analysis of the deviations between predicted and actual angles of 2640 protein chains (Zhou and Zhou, 2004). $\mathrm{\Delta }{\tau }_{A_I,S_I}^0$ is chosen so that $\mathrm{\Delta }{\tau }_{A_I,S_I}^0$ is greater than the deviations between predicted and actual angles for 70% of residues of type A_I and secondary structure S_I.

The DFIRE energy function ( $E_{ij}^{\mathit{DFIRE}}(r)$)

A statistical energy function based on the distance-scaled finite ideal-gas reference state is used to calculate the interaction energy function between two atoms i and j (C_α and C_β atoms only) at a distance r apart (Zhou and Zhou, 2002; Zhou et al., 2006). A version with finer distance bins (DFIRE 2.0) is used (Yang and Zhou, 2008b).

Hydrogen bonding energy (E^h-bond)

We adopted a continuous version of an empirical hydrogenbonding energy (Gong et al., 2005; Kortemme et al., 2003) for backbone atoms as follows:

$$E^{h-\mathit{bond}}=w_{hb}\sum _{I,\mid J-I\mid >3}{w}_{O_I{H}_J}{f}_r(r_{O_I{H}_J})f_{\theta }({\theta }_1,{\theta }_1^0)f_{\theta }({\theta }_2,{\theta }_2^0)$$ (4)

with

$$f_r(r)=\{\begin{array}{cc}0,& r\le 1.75A,\\ 1,& 1.75A<r<2.25A,\\ 4{(r-2.75)}^2,& 2.25\text{A}<r\le 2.75A\\ 0,& r>2.75A\end{array}$$ (5)

and

$$f_{\theta }(\theta ,{\theta }^0)=\{\begin{array}{cc}1,& cos\theta \le cos{\theta }^0-0.25,\\ 4(cos{\theta }^0-cos\theta ),& cos{\theta }^0-0.25<cos\theta \le cos{\theta }^0,\\ 0,& cos\theta >cos{\theta }^0,\end{array}$$ (6)

where r is the distance between atoms H and O, θ₁ is the angle C-O-H, θ₂ is the angle O-H-N, ${\theta }_1^0={120}^{\circ },{\theta }_2^0={126.9}^{\circ }$, w_hb = 10, and w_OIHJ is a proportionality constant to distinguish nonlocal hydrogen bonds (|I − J | > 4) from local hydrogen bonds (|I − J | = 4, separated by four sequential residues between a hydrogen-bond donor of residue J, H_J, and a hydrogen-bond acceptor of residue I, O_I, no hydrogen bonds were included for |I − J | < 4). We set w_OIHJ= 1.0 for local hydrogen bonds, 3.6 for nonlocal hydrogen bonds between predicted strand residues, 0.6 for nonlocal hydrogen bonds between predicted helical residues, and 1.2 for other nonlocal hydrogen bonds. These values were obtained by trial and error. Here, we have increased weights for strands because they are entropically more difficult to form. Secondary structures are predicted by an improved version of SPINE (Dor and Zhou, 2007a; Faraggi et al., 2009). The different geometric parameters for the angles C-O-H ( ${\theta }_1^0$) and O-H-N ( ${\theta }_2^0$) are based on statistical analysis of protein structures (Kortemme et al., 2003). We neglect the hydrogen-bond energy for |I − J | ≤ 3 because the DFIRE energy function captures local interactions adequately (Yang and Zhou, 2008a; Yang and Zhou, 2008b).

The energy function

The final energy function is the sum of the three terms described above. That is,

$$E=\sum _I(E_I^{\phi }+E_I^{\psi })+\sum _{i>j}{E}_{ij}^{\mathit{DFIRE}}(r)+E^{h-\mathit{bond}}.$$ (7)

Initial setup

Proteins are represented by main-chain atoms (N, C_α, C, O, and H) and C_β atoms only and are described by internal coordinates: the bond lengths, covalent-bond angles, and backbone torsion angles of ϕ, ψ, and ω. The bond lengths and covalent angles are fixed to ideal values from the CHARMM force field (Brooks et al., 1983) except for the covalent angle between backbone N, C_α and C atoms. This angle is initially set to the ideal value of 111.6° but is allowed to change within 10° from the ideal value so that a local minimization technique can be employed (as described below). The planar torsion angle ω is fixed to 180° while the initial backbone ϕ/ψ angles are assigned in the following way. When predicted angle restraints are not employed ( $E_I^{\phi }=E_I^{\psi }=0$), ϕ/ψ angles are assigned randomly according to the observed residue-specific probability in the 2640 proteins (Zhou and Zhou, 2004). When predicted angle restraints are employed, backbone angles are randomly assigned with a random value within a range ( $\mathrm{\Delta }{\phi }_{A_I,S_I}^0$ and $\mathrm{\Delta }{\psi }_{A_I,S_I}^0$) around the predicted ${\phi }_I^{\mathit{pred}}$ or ${\psi }_I^{\mathit{pred}}$ angles.

Local optimization

We used two types of moves for local energy optimization: pivot move and local “fixed-end” moves (Betancourt, 2005). In a pivot move, a random value between −10° and 10° is added to the ϕ and ψ angles for a randomly selected residue I. In “fixed-end” moves, two residues, I and J, are chosen randomly with their sequence positions 2 to 10 residues apart (2 ≤ |I − J | ≤ 10). The atoms in between the C_α atom of residue I and that of residue J are then rotated along the axis of the two C_α atoms by an angle randomly chosen with a constraint that the covalent angle between N, C_α and C atoms does not deviate more than 10° from its ideal value (111.6°) after the rotation. After each move, the Metropolis criterion is employed to accept or reject the move with a Boltzmann factor: 0.01ΔE^l−1, with ΔE^l−1 the root-mean squared energy value of all conformations in the last generation, l−1, and the effective temperature is set to a low value of 0.01. Because a pivot move often leads to a large change in a protein’s conformation and reduces the acceptance rate of moves, we gradually reduced the probability to make a “pivot move” from 1.0 to 0.0 in the first 30% of moves from a total of 30N moves of local optimization for a protein of chain length N.

Genetic Algorithm (GA)

The genetic algorithm described below is modified slightly from what was used for ab initio refolding of terminal fragments (Yang and Zhou, 2008a). We used N_p (=160) parents for the genetic algorithm. Initial N_p conformations are generated (initial setup) and locally optimized (local optimization). These optimized conformations serve as the first-generation parent conformations, and are used to generate another N_p conformations by crossover, mutations and local optimization. This leads to 2N_p conformations that are clustered as follows: The lowest energy conformation is chosen as the representative conformation of the first cluster which contains all the conformations with a drms of 5Å or less from the conformation. drms is the root-mean-squared difference between the pairwise distances of the two conformations. Then, the lowest energy conformation from the remaining conformations is chosen as the representative conformation of the second cluster. This process continues until all conformations are clustered. We employed a fitness function: $f_m^l=exp(-E_m/\mathrm{\Delta }{E}^{l-1})/({\rho }_m{o}_m)$ where E_m is the energy of conformation m, ρ_m is the number of conformations in the cluster that conformation m belongs to, $o_m(=1+0.3n_m^g)$ mimics the age of the conformation m that is related to number of generations the conformation m existed, $n_m^g$. To ensure structural diversity, the first 30 conformations for the next generation are chosen from the first 30 clusters, respectively, according to the above fitness function. The remaining 130 conformations are chosen according to the fitness function from the remaining 290 conformations. A maximum of 400 generations is used in protein conformational search.

D. Effect of homologs

One question is if the existence of homologs between training and test proteins will increase the accuracy of predicted angles when we compared our angle-prediction results with TOPOS (11 protein set (Cavalli et al., 2007)) and TALOS (37 protein set) and employed them in structure prediction (16 protein set (Bradley et al., 2005)). To answer this question, we made a specific prediction server that was trained without sequence homologs to the 16 proteins used for structure prediction. We found that the average accuracy of 16 proteins changes only 0.6% (Q_60° =88.8% with homologues versus 88.2% without). This highlights our effective use of overfitting protection in training. Here, we have performed structure prediction using a server trained without sequence homologues.