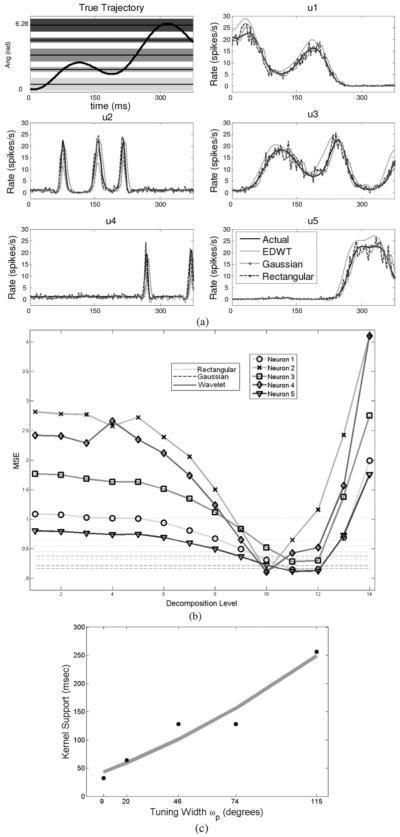
Fig. 6.

(a) Top-left: 400 ms segment of angular direction from a movement trajectory superimposed on tuning “bands” of five representative units. Top right, middle, and bottom panels: Firing rates obtained from the point process model for five units and their extended DWT (EDWT), Gaussian, and rectangular kernel estimators. As expected, the rectangular kernel estimator is the noisiest, while the Gaussian and EDWT estimators are closest to the true rates. (b) Mean square error between the actual (solid black line) and the estimated firing rate for each neuron with the three methods. Each pair of dotted and dashed lines is the MSE for rectangular and Gaussian kernel methods, respectively, for the five units in (a). These remain flat as they do not depend on the DWT kernel window length. For the sharply tuned neurons, on average, ten levels of decomposition result in a minimum MSE that is lower than the MSE for rectangular and Gaussian kernel methods. For broadly tuned neurons, 12 levels of decomposition result in optimal performance. (c) Tuning width versus optimal kernel size. As the tuning broadens, larger kernel windows (i.e., coarser time scales) are needed to obtain optimal rate estimators.