Ionic and pH effects on the osmotic properties and structure of polyelectrolyte gels

Abstract

We investigate the effects of salt concentration and pH on neutralized poly(acrylic acid) (PAA) gels in near physiological salt solutions. Either adding calcium ions or decreasing the pH are found to induce reversible volume transitions but the nature of these transitions seems to be different. For example, the osmotic pressure exhibits a simple power law dependence on the concentration as the transition is approached in both systems, but the power law exponent n is substantially different in the two cases. On decreasing the pH the value of n gradually increases from 2.1 (at pH = 7) to 3.2 (at pH = 1). By contrast, n decreases with increasing calcium ion concentration from 2.1 (in 100 mM NaCl solution) to 1.6 (0.8 mM CaCl₂ in 100 mM NaCl solution). In both systems, a strong increase of the small-angle neutron scattering intensity (SANS) is observed near the volume transition. The SANS results reveal that calcium ions favor the formation of linearly aligned regions in PAA gels.

INTRODUCTION

A polyelectrolyte gel is a charged, crosslinked polymer network immersed in a fluid. In their pioneering studies Tanaka and colleagues demonstrated that swollen polyeletrolyte gels are capable of undergoing large, discrete transition in equilibrium volume in response to changes in the environmental conditions, such as solvent composition and temperature.^1–5 They demonstrated that ionization of the network chains plays an essential role in these transitions.^4,5 This controllable volume behavior has led to numerous applications of polyelectrolyte gels, including drug delivery, superabsorbent materials and microfluidic devices.

Several biological processes involve changes in the ionic environment (ion concentration and valence, pH). Tasaki at al. emphasized the similarity between volume transitions induced by divalent ions and the rapid structural changes observed during excitation of nerve fibers.⁶.⁷ In the context of cartilage biomechanics there is an ample literature dealing with the swelling of polyelectrolyte gels.^8–10 Several authors proposed multiphase fluid models for cartilage that include osmotic effects. There is evidence that certain ionic constituents (e.g., CaCl₂, NaCl, KCl, pH) of cervical mucus show cyclic variations during the menstrual cycle.^11,12 It is however not fully understood how these changes affect mucus hydration and its structure and mechanical (viscoelastic) properties. In addition, ion-polymer interactions have importance in many technological and scientific applications as diverse as food preservation and plastic battery technology.

Previously we made systematic measurements on a variety of synthetic and biopolymer solutions and gels using an array of complementary experimental techniques to determine the effect of multivalent ions on the structure and dynamic properties over a wide range of length and time scales.^13–17 It was found that in near physiological salt concentration the thermodynamics of gel swelling can be described by a formalism similar to that of neutral polymer gels.¹³ Anomalous small-angle X-ray scattering measurements revealed significant differences between the distribution of monovalent and divalent counterions in the ion cloud surrounding the charged macromolecules.^17,18 Divalent ions form a compact layer around the oppositely charged polyelectrolyte chains while the spatial extent of the monovalent ion cloud is much larger.

In this work, we compare the effect of salt concentration and that of the pH on the macroscopic osmotic properties of polyelectrolyte gels. In neutralized polyacrylic acid gels (polyacrylic acid sodium salt) either adding divalent ions or decreasing the pH can induce reversible volume transitions. It will be shown that the variation of the osmotic pressure on approaching the transition is substantially different in the two experiments. Small-angle neutron scattering (SANS) measurements are made to identify structural differences between the two cases.

The outline of the paper is as follows. The Introduction is followed by a brief summary of the theoretical background discussing (i) the thermodynamics of gel swelling and (ii) the scattering formalism used to analyze the SANS measurements. The next section describes the model system and the sample preparation. Then the experimental results are presented and discussed. Finally, the last section summarizes the conclusions.

THEORY

Gel Swelling

The swelling behavior of a homogeneous neutral polymer gel can be described through the osmotic swelling pressure Π_sw, which consists of elastic Π_el and mixing Π_mix contributions.¹⁹ Thermodynamic equilibrium is attained when the chemical potential of the solvent is equal inside and outside the swollen network, i.e., no net solvent transfer occurs between the gel and the surrounding liquid or vapor phase. At equilibrium with pure solvent the elastic and mixing pressures compensate each other and Π_sw = 0. However, in the general case the solvent activity in the gel is smaller than that of the pure solvent, and we have

$${\Pi }_{\mathrm{mix}}+{\Pi }_{\mathrm{el}}={\Pi }_{\mathrm{sw}}>0$$ (1)

The elastic pressure of the gel can be estimated from the theory of rubber elasticity ^19,20

$${\Pi }_{\mathrm{el}}=-\mathrm{G}$$ (2)

where G is the elastic (shear) modulus.

According to the scaling theory²¹ in the semidilute concentration range the osmotic pressure of neutral polymer solutions is given by

$${\Pi }_{\mathrm{mix}}=\mathrm{A}{\phi }^{\mathrm{n}},$$ (3)

where A and n are constants and φ is the volume fraction of the polymer. The constant A = N_Ak_BT/v, where N_A is the Avogadro number, k_B the Boltzmann constant, T the absolute temperature, and v the molar volume of the solvent. The exponent n depends on the thermodynamic quality of the solvent [n ≈ 9/4 (good solvent condition) and n = 3 (theta condition) for flexible polymer chains], and chain stiffness, which can be influenced by the charge interactions.

In polyelectrolyte solutions the concentration dependence of Π_mix can be estimated based on the following simple scaling model. In the absence of added salt polyelectrolyte molecules are almost fully extended due to the repulsive electrostatic interaction between the charged groups. In such systems the overlap concentration φ* is given by

$${\phi }^{\ast }\propto \mathrm{N}∕{\mathrm{N}}^3\propto {\mathrm{N}}^{-2}$$ (4)

where N is the number of monomer units in the chain.

In the dilute concentration range the osmotic pressure is proportional to φ/N while in the semidilute regime it becomes independent of N. In the intermediate region Π_mix should obey the following scaling relation

$${\Pi }_{\mathit{mix}}\propto \frac{\phi }{N}{f}_{\Pi }{\left(\frac{\phi }{{\phi }^{\ast }}\right)}^y$$ (5)

where the function f_Π(x) has the following limiting properties

$$f_{\Pi }\left(x\right)=\{\begin{array}{cc}1\hfill & (\phi ⪡{\phi }^{\ast })\hfill \\ {\left(\frac{\phi }{{\phi }^{\ast }}\right)}^{\mathrm{y}}\hfill & (\phi >{\phi }^{\ast })\hfill \end{array}\phantom{\}}$$ (6)

Since in the semidilute regime Π_mix no longer depends on N the value of the exponent must be y = 1/2, and we get

$${\Pi }_{\mathrm{mix}}\propto {\phi }^{3∕2}.$$ (7)

The osmotic pressure of polyelectrolyte solutions also contains an ionic contribution. The ionic term Π_ion can be estimated from the Donnan model that accounts for the unequal concentration of ions inside and outside the swollen network.¹⁹ Thus, the swelling pressure of the polyelectrolyte gel is given as

$${\Pi }_{\mathrm{sw}}={\Pi }_{\mathrm{mix}}+{\Pi }_{\mathrm{el}}+{\Pi }_{\mathrm{ion}}=\mathrm{A}{\phi }^{3∕2}-\mathrm{G}+N_A{k}_{B}T\sum _i(c_i-c_i^{\ast })$$ (8)

where A is a constant, and c_i and c_i* are the concentration of the i ionic species inside and outside the swollen network, respectively.

Small-Angle Neutron Scattering

The analysis of the SANS response of an uncharged polymer gel contains at least two contributions. At low values of the scattering wave vector q [= (4π/λ)sin(θ/2), where λ is the wavelength of the radiation and θ the scattering angle] the scattering signal is dominated by large inhomogeneities frozen-in by the cross-links.^22,23 The typical distance scales probed in this region are much greater than the average distance between the polymer chains. Due to their large size these objects do not contribute to the thermodynamic properties of the system. At larger q values the thermodynamic fluctuations are probed and their contribution to the scattering response can be determined. In the highest q region the scattering experiment yields information on the local structure of the chains. In this region, however, incoherent scattering and uncertain background subtraction may impose severe limitations. Hence, in the simplest case, the measured intensity is written as

$$I\left(q\right)=I_{\mathit{stat}}\left(q\right)+I_{\mathit{fluct}}\left(q\right)+\mathrm{background}$$ (9)

In semidilute polymer solutions the second term can be approximated by a Lorentzian form factor

$$I_{\mathit{fluct}}\left(q\right)=\frac{I_{\mathit{fluct}}\left(0\right)}{1+q^2{\xi }^2}$$ (10)

In eq. 10 the intensity of the fluctuating component at q = 0 is denoted as I_fluct(0), and ξ represents the correlation length of the thermodynamic concentration fluctuations.

EXPERIMENTAL

Sample Preparation

Sodium polyacrylate (PAA) gels were prepared by free-radical copolymerization of acrylic acid and N,N'-methylene-bis-acrylamide) crosslinker in aqueous solution according to a procedure described previously.²⁴ Ammonium persulfate was added to the nitrogen-bubbled solution containing partially neutralized acrylic acid and N,N'-methylene-bis-acrylamide. The monomer concentration was 30% (w/w), and 35% of the acrylic acid monomers were neutralized by sodium hydroxide prior to polymerization. The crosslinker concentration was 0.3 % (w/w). The crosslinking process was carried out at 80 °C for two hours. After gelation, gels were washed with deionized water, fully neutralized and swollen in 100 mM NaCl solution (nearly physiological condition). The pH in the surrounding liquid phase was adjusted with HCl solution. The calcium ion concentration was varied from zero to 0.8 mM by adding CaCl₂ (dissolved in 100 mM NaCl solution) to the equilibrium liquid.

Osmotic Swelling Pressure Measurements

PAA gels were equilibrated with aqueous solutions of poly(vinyl pyrrolidone) (PVP, molecular weight: 29 kDa) of known osmotic pressure.^25,26 A semipermeable membrane (dialysis bag) was used to separate the swollen network from the PVP solution. The membrane prevented the penetration of the polymer molecules into the gel. At equilibrium, the swelling pressure of the gel inside the dialysis bag is equal to the osmotic pressure of the PVP solution outside. The concentration of the gel was measured when equilibrium was attained. The reversibility of the deswelling process was checked by transferring the deswollen gels into PVP solutions having different osmotic pressures. It was assumed that the salt concentration and pH in the liquid phase outside the gel sample was unchanged (infinite bath).

Shear Modulus Measurements

Shear moduli of the gels were determined from uniaxial compression measurements made on gel cylinders using a TA.XT2I HR Texture Analyser (Stable Micro Systems, UK).²⁴ Gel samples were transferred from the dialysis bag into this apparatus, which measures the deformation as a function of the applied force. Stress-strain isotherms were determined at 25^□°C in about 3–5 min with no detectable change in gel composition. The absence of volume change and barrel distortion was carefully checked. The stress-strain isotherms were found to fit the Mooney-Rivlin relation. Under these experimental conditions, the shear modulus can be calculated from the nominal stress, σ (force per unit undeformed cross-section), using the relation

$$\mathrm{G}=\sigma ∕(\Lambda -{\Lambda }^{-2})$$ (11)

where Λ is the deformation ratio. Measurements were carried out in the range 0.7 < Λ < 1.

Small-Angle Neutron Scattering

Small-angle neutron scattering (SANS) measurements were performed on the NG3 SANS instrument at the National Institute of Standards and Technology (NIST) Center for Neutron Research (NCNR) in Gaithersburg, MD. Measurements were made at three sample-to-detector distances (1.2 m, 4 m and 13.1 m) with an incident wavelength of 8 Å. Standard NIST sample cells of 2 mm path length were used. Data were collected on a two-dimensional detector in the scattering vector range 0.003 Å⁻¹ < q < 0.4 Å⁻¹. The data were corrected for background and empty cell scattering.²⁷

RESULTS AND DISCUSSION

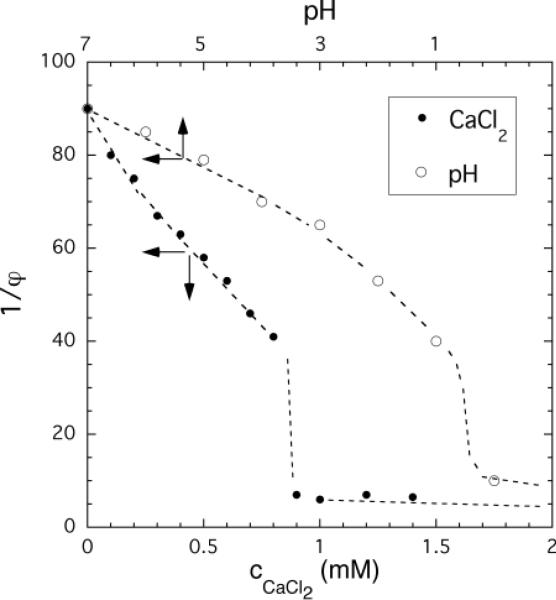
Figure 1 shows the equilibrium swelling curves of PAA gels in 100 mM NaCl solutions

Figure 1.

Dependence of the swelling degree (1/φ) of PAA gels on the pH (upper x-axis) and CaCl₂ concentration (lower x-axis) of the equilibrium 100 mM NaCl solution.

(i) at different values of pH, and

(ii) at different CaC1₂ concentrations (at pH = 7).

The abscissa represents the pH (upper axis) and the CaCl₂ concentration (lower axis) and the ordinate represents the swelling degree of the PAA gels. It can be seen that either decreasing the pH or increasing the calcium ion concentration induces large, apparently discontinuous volume changes. In the vicinity of the transition thresholds, the gels undergo a significant volume change in response to minute changes in pH or CaCl₂ concentration. In 100 mM NaCl solution the transition occurs at pH ≈ 0.5 or c_CaCl2 ≈ 0.9 mM.

Previous studies demonstrated that changes in the ionic environment are associated with changes in the osmotic swelling pressure.^13,24,28 It was also shown that in near physiological ionic conditions the electrostatic contribution (third term in equation 8) is negligible, i.e., the osmotic pressure of the cross-linked polymer can be estimated from the equation

$${\Pi }_{\mathrm{mix}}={\Pi }_{\mathrm{sw}}+\mathrm{G}$$ (12)

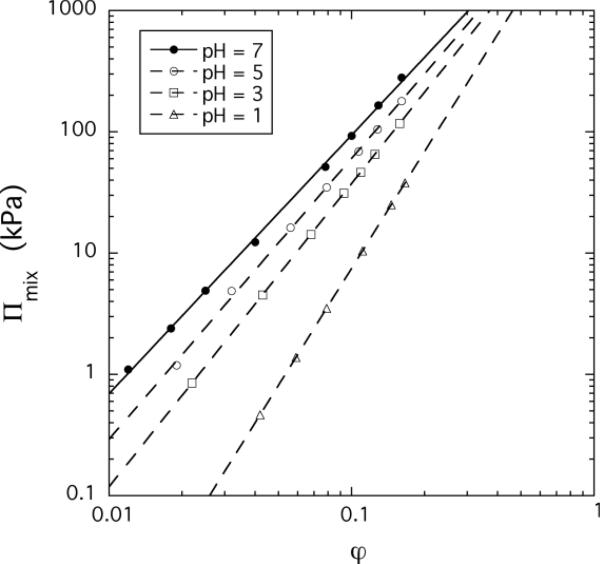
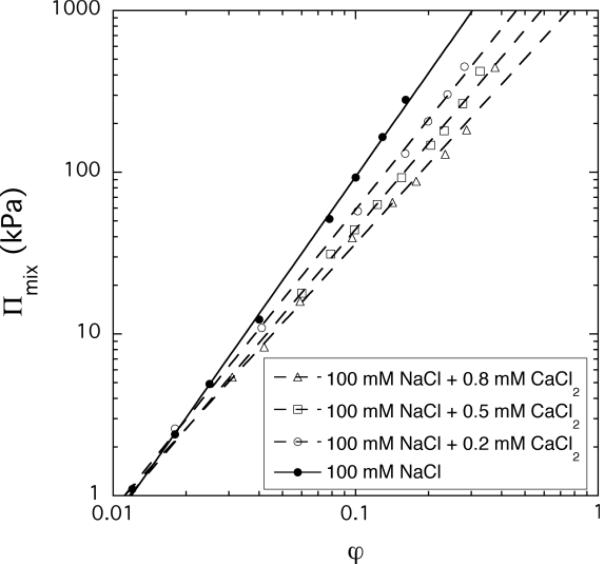
Using equation 12 we determined Π_mix for PAA gels at constant pH (pH: 7, 5, 3 and 1), and CaCl₂ concentration (c_CaCl2: 0, 0.2, 0.5 and 0.8 mM in 100 mM NaCl solution). In Figure 2a and b are displayed Π_mix as a function of the polymer volume fraction for both cases. In the double logarithmic representation each of the Π_mix vs φ curves is linear over the whole concentration range explored indicating that the osmotic pressure exhibits a simple power law dependence as predicted by the scaling theory.

Figure 2.

Variation of the osmotic pressure Π_mix with the polymer volume fraction at different values of pH (figure a) and CaCl₂ concentrations (figure b).

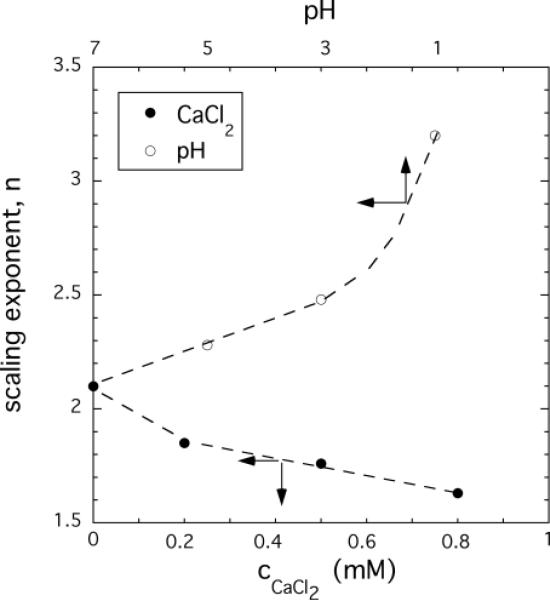
We analyzed the osmotic pressure data in terms of equation 3. Figure 3 shows the variation of the exponent n as a function of the pH (open circles) and the CaCl₂ concentration (filled circles). In 100 mM NaCl solution at pH = 7 the experimental value of n is 2.1, close to its good solvent value, suggesting that the electrostatic repulsive charges are largely screened. According to the scaling theory of Π_mix for neutral polymer gels, the scaling exponent should increase from 2.25 (good solvent condition) to 3 (theta condition). The dependence observed with decreasing pH shows a qualitatively similar behavior: the value of n gradually increases from 2.1 (at pH = 7) and at low pH it exceeds the theta value (n = 3.2 at pH = 1). Formally, the exponent n should diverge (n→∞) for compact polymers, so this tendency is consistent with the onset of a “coil-globule” transition.^29–31 Coil-globule transitions have been reported by Tanaka et al. for anionic polymer gels in which volume transitions were induced in response to changes in temperature and solvent composition.^32,33

Figure 3.

Dependence of the scaling exponent n on the pH (upper x-axis) and CaCl₂ concentration of the equilibrium 100 mM NaCl solution (lower x-axis).

The pH-dependence of the osmotic pressure of PAA gels is understandable in terms of the electrostatic attraction between the negative charges on the polymer chain and the positive protons. In a weak polyacid such as PAA, the apparent dissociation constant pK_a is defined as

$${\mathrm{pK}}_{\mathrm{a}}=\mathrm{pH}-{\mathrm{k}}_{\mathrm{B}}\mathrm{T}\log [\alpha ∕(1-\alpha )]$$ (13)

where α is degree of dissociation that defines the effective charge of the polyelectrolyte molecule. As the pH decreases the degree of protonation increases. Since water is a good solvent for the charged state and a poor solvent for the neutral (hydrophobic) state, the conformation of the polyelectrolyte chain is expected to undergo from the expanded coil to the contracted globule state with decreasing pH. The similarity between the behavior of polyelectrolyte gels as a function of pH and neutral polymer gels as a function of the solvent quality suggests that in both cases thermodynamic properties are dominated by short-range interactions.

Figure 3 shows that in the calcium containing system the variation of the power law exponent is opposite: n decreases on approaching the transition. This finding indicates that the influence of calcium ions on the molecular conformation and thermodynamic interactions may be significantly different from that of the pH. Ion polymer interactions can induce conformational changes, and modify other polyelectrolyte properties.

Although substantial amount of knowledge is available for monovalent ions based on the Poisson-Boltzmann model and other approaches, relatively little is known with respect to multivalent ions. In general, monovalent ions bind weakly to the polyelectrolyte molecules. By contrast, multivalent ions interact strongly with the oppositely charged chains. In the presence of multivalent ions the Poisson-Boltzmann approximation breaks down and the situation becomes much less clear. Recent anomalous X-ray scattering (ASAXS) measurements have revealed significant differences between the spatial distribution of monovalent and divalent counterions around the polyelectrolyte chains.¹⁷ Mobile monovalent ions form an extended diffuse ion cloud while divalent ions are located in the immediate vicinity of the macroion. It is expected that replacement of Na ions by H or Ca ions significantly modifies the ion distribution and the thermodynamic interactions in the polymer-solvent system. Computer simulations suggest a strong coupling between ion binding and conformational degrees of freedom.³⁴ Although, experimental and computational studies indicate that both short-range and long-range interactions and the interplay between them are important, no detailed understanding of the physical properties of polyelectrolyte systems exists, in particular the relationship between the structure and solution thermodynamics is poorly understood.

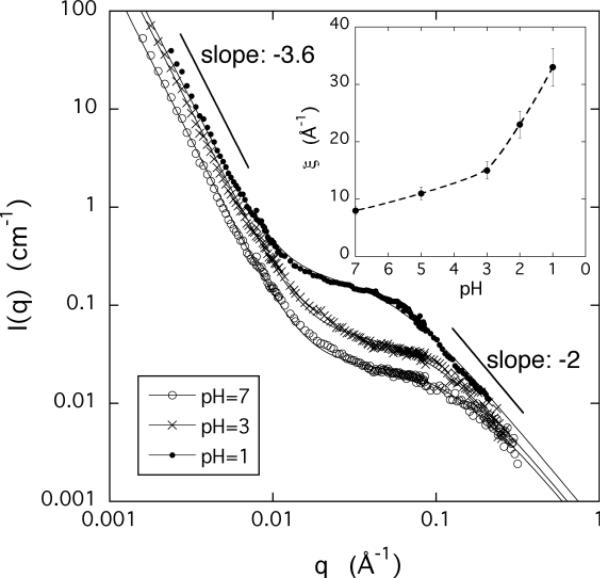
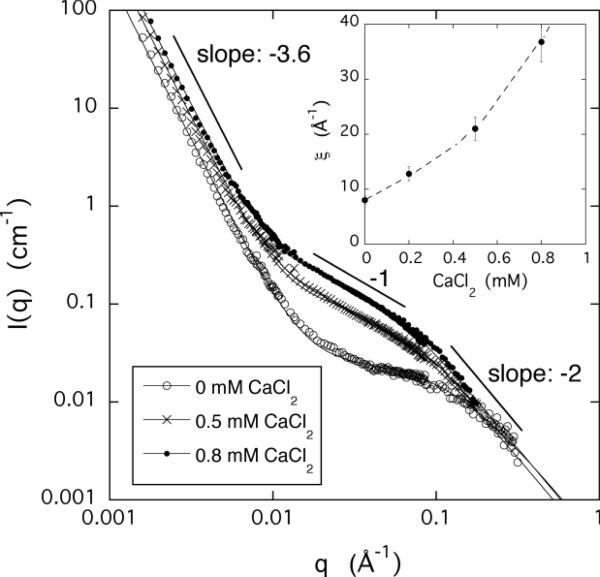
We made SANS measurements to identify differences between the structures formed either by decreasing the pH or adding calcium ions to PAA gels. Figures 4a and 4b show the scattered intensity I(q) for both cases. At low and high values of q changes in the ionic environment have no significant influence on the scattering responses. In the low q region (q < 0.01 Å⁻¹) the scattering intensity sharply decreases with a slope of approximately −3.6. The intense scattering at low q is typical of polyelectrolyte systems and can be attributed to scattering from large clusters.^35,36 The size of these objects (> 1000 Å) exceeds the resolution of the SANS measurements. In the high q region (q > 0.07 Å⁻¹) the SANS intensity is governed by the chain geometry (cross-sectional radius of PAA chain). The data show that the ion exchange process does not affect appreciably the low and the high q scattering features. Response to changes in the ionic environment (ion concentration and valence, pH) is confined to the intermediate q range.

Figure 4.

SANS spectra of PAA gels measured at different values of pH (figure a) and CaCl₂ concentrations (figure b). Insets show the variation of the correlation length ξ as a function of pH and CaCl₂ concentration, respectively.

It is evident that the intensity of the scattered signal increases with decreasing pH or increasing calcium ion concentration, as expected for a system approaching phase transition. This increase can be analyzed using the Ornstein-Zernike formalism in order to calculate the correlation length of the concentration fluctuations that develop in the swollen network. In Figures 4a and 4b the continuous curves are least squares fits of eq. 9 to the SANS spectra. In the curve fitting equation the first term (I_stat) is approximated by a simple power law of the form Cq^−m, where C and m are constants, and the second term (I_fluct) has a Lorentzian shape. As seen from the insets, the correlation length ξ increases close to the volume transition, but remains finite in the whole pH and calcium concentration range that could be analyzed.

It can also be seen that calcium ions affect not only the intensity, but also the shape of the SANS curves in the intermediate q-region. In calcium containing gels, in a limited range of q, the measured intensity varies as q⁻¹, which extends towards lower q values with increasing calcium ion concentration. The q⁻¹ dependence of the scattering signal suggests that divalent/monovalent ion-exchange favors the formation of linearly aligned assemblies. Ion mediated self-assembly frequently occurs in polyelectrolyte solutions and several theoretical explanations have been proposed to account for this phenomenon. However, bundle formation is typically observed in solutions of relatively rigid polyelectrolytes such as DNA, or rod-like filaments such as F-actin. The substitution of two monovalent counterions by a single divalent counterion (Ca) modifies the charge distribution in the vicinity of the chain: the spatial extent of the counterion cloud is reduced and the rigidity of the chain may also be affected. The present results indicate that even flexible polyelectrolyte chains can self-assemble into fiber-like structures under appropriate ionic conditions in aqueous solutions containing both monovalent and divalent counterions.

CONCLUSIONS

We have studied the effects of pH and calcium ion concentration on the swelling and scattering response of PAA gels in near physiological salt solutions. Under these conditions, the osmotic contribution from the free ions (Donnan term) is negligible, and gel swelling is driven by the osmotic pressure of the network polymer.

It has been demonstrated that both decreasing the pH and adding calcium ions induce reversible volume transitions in these gels. In both systems, the concentration dependence of the osmotic pressure exhibits a simple power law behavior. Osmotic pressure measurements and SANS observations indicate that substantial differences exist between the effect of pH and multivalent counterions. On decreasing the pH the power law exponent increases from 2.1 (pH = 7) to 3.2 (pH = 1) implying that at low pH the polyelectrolyte chains behave like neutral polymers in poor solvent. Upon addition of calcium ions the power law exponent of the osmotic pressure vs concentration curves markedly decreases from 2.1 (calcium-free solution) to 1.6 (0.8 mM CaCl₂ in 100 mM NaCl solution). SANS measurements reveal that calcium ions favor the formation of linearly aligned regions, indicating that under appropriate ionic conditions flexible polyelectrolyte chains self-assemble into linear arrays.