Dependence of Macroscopic Wetting on Nanoscopic Surface Textures

Abstract

The hydrophobicity of a surface can be enhanced by physical textures. However, no existing theories of surface wetting can provide guidance to pinpoint the texture size requirement to achieve super/ultrahydrophobicity. Here, we show that the three-phase contact line tension, τ, is an important link to understand the dependence of macroscopic wetting on physical texture size in an ideal Cassie regime. Specifically, we show that texture size is the dominant parameter in determining surface hydrophobicity when the size approaches a limiting physical length scale, as defined by τ and the surface tension of the liquid.

Introduction

Many natural surfaces on animals, insects, and plants are highly hydrophobic.^1–5 Water droplets on these natural surfaces maintain a near-spherical shape and roll off easily, carrying the dirt away with them.^1,5 These observations have led to enormous interests in manufacturing biomimetic water-repellent surfaces owing to their broad spectrum of potential applications, ranging from liquid-repellent fabrics to friction-reduction surfaces.^6–19 The governing mechanism of the observed high surface hydrophobicity is typically explained by the well-known Cassie–Baxter equation developed in 1944.²⁰ Since the maximum contact angle on a smooth surface can only reach ∼120°,²¹ the Cassie–Baxter equation suggests that physical textures are required to further enhance the surface hydrophobicity. Specifically, the equation relates the most stable apparent equilibrium contact angle (i.e., θ*) of a liquid droplet suspended on a textured surface^22,23 to its solid fraction (i.e., the portion of solid region that is in touch with the liquid droplet contact area, Φ_s)²⁴ and its material surface property (i.e., the equilibrium contact angle on a smooth surface, θ),

$$cos{\theta }^{\ast }=-1+{\Phi }_{\text{s}}(cos\theta +1)$$ (1)

An important physical insight provided by the classical equation is that a high water apparent equilibrium contact angle (i.e., θ* ≥ 150°) can be achieved by reducing the texture solid fraction (i.e., Φ_s< 0.1) of hydrophobic surfaces (i.e., θ ≥ 90°).

Experimentally, the most stable apparent equilibrium contact angle of a water droplet on a textured surface can be difficult to attain. Liquid droplets sitting on the textured surface exhibit a variety of contact angles bound by two extreme values. The upper limit is known as the apparent advancing contact angle ( ${\theta }_{\text{A}}^{\ast }$), whereas the lower limit is referred as the apparent receding contact angle ( ${\theta }_{\text{R}}^{\ast }$). The difference between these values is known as contact angle hysteresis (i.e., $\Delta {\theta }^{\ast }={\theta }_{\text{A}}^{\ast }-{\theta }_{\text{R}}^{\ast }$, where ${\theta }_{\text{A}}^{\ast }\ge {\theta }^{\ast }\ge {\theta }_{\text{R}}^{\ast }$), whose physical origin is attributed to liquid contact line (CL) pinning to the physical roughness and chemical heterogeneity present on solid surfaces.^6,25–28 By minimizing the contact angle hysteresis (i.e., Δθ* ∼ 0), textured surfaces with extremely high water repellency can be achieved.²⁹

While most of the real surfaces show finite contact angle hysteresis, some exceptions were found in recent literature. For example, it is demonstrated that natural and artificial surfaces with texture sizes on the order of 1–100 nm show superior water repellency (i.e., ${\theta }_{\text{A}}^{\ast }\sim {\theta }_{\text{R}}^{\ast }$),^{4,15,16,19,30,31} which indicates that the apparent water contact angles on these surfaces are very close to the most stable equilibrium values (i.e., ${\theta }_{\text{A}}^{\ast }\sim {\theta }^{\ast }\sim {\theta }_{\text{R}}^{\ast })$. In addition, some of these nanostructured surfaces, such as tokay gecko^2,30 and mosquito Culex pipiens,⁴ can maintain their superhydrophobicity (i.e., 150° ≤ θ* < 180°)⁷ even with a high texture solid fraction (i.e.,Φ_s ≥ 0.1). This observation contradicts the theoretical prediction by the Cassie–Baxter equation. Furthermore, recent experiments showed that engineered hydrophobic surfaces with textures on the order of nanometers are purely ultrahydrophobic (i.e., θ* ∼ 180° and Δθ* ∼ 0).^15,16,19 All of these experimental observations indicate that physical texture size, in addition to texture solid fraction, may play an important role in determining macroscopic surface hydrophobicity, which was not explicitly described in the classical and contemporary theories of surface wetting.^{20,23,32–39}

In this Letter, we aim to provide a quantitative understanding on the relationship between surface hydrophobicity and physical texture size. Specifically, we show that CL tension at a three-phase interface, τ, is an important link to understand the dependence of macroscopic wetting on nanoscopic surface textures.

Theoretical Section

The concept of τ was first introduced by Gibbs in the 1870s,²⁵ where it is defined as the excess free energy of a three-phase system per unit length of a CL.^40,41 The physical origin of τ stems from the intermolecular forces of the molecules distributed along and in the vicinity of the CL acting upon each other.⁴⁰ To understand how the three-phase CL formation influences the macroscopic wetting process, we consider a situation where a macroscopic liquid droplet suspends on a textured surface with cylindrical protrusions of radius r and solid fraction Φ_s (Figure 1). In particular, a number of key assumptions are made for this physical model: (1) the droplet size (or wetting radius) is much larger than that of the surface textures,²² yet smaller than the capillary length of the liquid; (2) small or negligible constraint of the three-phase CL at the protrusion edge (i.e., pinning is small or negligible); and (3) the liquid droplet is in an ideal Cassie regime (i.e., no liquid penetration into the surface textures). Under the droplet contact region, three-phase CLs are formed at the protrusion perimeters. Infinitesimal displacement of the CL is energetically favorable when the energy changes associated with the formation/destruction of new interfacial CL and surfaces lower the total energy of the three-phase system. For a very small displacement of the CL, dR, the total free energy change, dE, before and after the movement of the CL can be expressed as dE = dE_surface+ dE_line, where dE_surface and dE_line are the changes of surface and line energies, respectively. In particular, the surface energy change can be expressed as dE_surface = Φ_s (γ_SL − γ_SV)dA + (1 − Φ_s) γ_LV dA + γ_LV dAcos θ*, where γ_SL, γ_SV, and γ_LV are the surface tensions of solid–liquid, solid–vapor, and liquid–vapor interfaces, respectively, and dA is the infinitesimal area change as the contact radius displaces by dR. In addition, the total line energy change is proportional to the infinitesimal length of the three-phase contact lines formed within dA and thus can be computed as dE_line=2τΦ_sdA/r (Supporting Information). By minimizing the total free energy change with respect to the contact area and applying the Young equation, we obtain a new governing equation which relates the texture size, r, to the most stable apparent equilibrium contact angle, θ* (Supporting Information),

Figure 1.

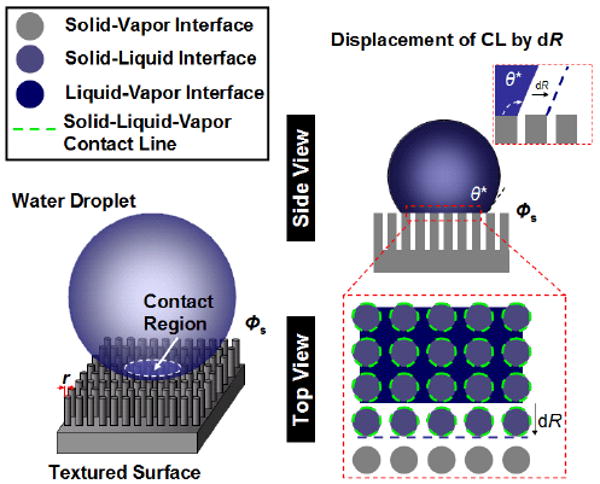
Wetting of a macroscopic water droplet suspended on a textured surface. The expansion of the infinitesimal three-phase CL is determined by the energy changes during the formation/destruction of the new local CLs and surfaces. When the line energy gained to form the local CL is comparable to the changes of surface energies, the expansion of the infinitesimal three-phase CL will be energetically unfavorable.

$$cos{\theta }^{\ast }=-1+{\Phi }_s(cos\theta +1)-\frac{2{\Phi }_s\tau }{r{\gamma }_{LV}}$$ (2)

Equation (2) presents a unified description of surface hydrophobicity on a textured surface with the contributions from both surface and line energies (Supporting Information).

Results and Discussion

The quantitative nature of τ is a critical parameter that dictates the length scale of textures for line energy contribution to become dominant. While the sign of τ remains a controversial issue in the field of surface wetting science, there is now general consensus on the magnitudes of τ.^40,41 For example, for a liquid droplet sitting on a flat surface, the CL tension is on the order of 10⁻¹² – 10⁻¹⁰ J/m, as verified by recent high resolution scanning microscopy measurements.^42,43 We denote this intrinsic form of CL tension as τ_intrinsic. In particular, when the characteristic curvature of a CL is on the order of τ_intrinsic/γ_LV, the influence of line energy is comparable to surface energy gained at the solid–liquid interface of a liquid droplet on a flat surface.⁴⁴ On the other hand, it is important to recognize that the molecular environments in the vicinity of the three-phase CL at a protrusion edge are different from that of the flat surface. The interaction of the CL with the protrusion edge may result in an extra energy barrier^26,45 due to CL pinning.^25,28,46 Using the Gibbs inequality condition of pinning at a protrusion edge,^25,47 one can show that the line energy barrier at the CL of an advancing liquid droplet, defined as τ_pinning, can be expressed as τ_pinning = pγ_LVr, provided that r is much smaller than the capillary length of the liquid and p is a non-negative coefficient that indicates the degree of pinning (Supporting Information). This suggests that τ at the protrusion edge may consist of two components; one is the intrinsic tension due to the intermolecular forces within and in the vicinity of the CL, and the other is the tension attributed to the interaction of the CL with the protrusion edge (i.e., τ = τ_intrinsic + τ_pinning). When pinning is negligible (i.e., p ∼ 0), the CL tension will be reduced to its intrinsic form (i.e., τ = τ_intrinsic).

We compared the proposed theoretical relationship with experimental data obtained from the well-characterized natural and artificial super/ultrahydrophobic surfaces equipped with cylindrical-like textures in the literature (Figure 2).^{4,10,12–14,16,19,30} Specifically, a defining characteristic for an ideal Cassie regime is signified by the low contact angle hysteresis of the surfaces (i.e., extremely high water repellency).⁴⁸ Therefore, only the experimental data on super/ultrahydrophobic surfaces that satisfied this criterion (i.e., Δθ* ≤ 10°) are used to compare with the theoretical model. Based on these data, we used eq 2 to compute the corresponding line tension magnitudes (Supporting Information). The experimental trend shows a reasonable correlation with the proposed relationship with τ_intrinsic = 1 ×10⁻¹⁰ J/m and the coefficient of τ_pinning, p = 0.23 (n = 8, C² = 0.80, where n and C are the number of experimental data points and the correlation coefficient, respectively). The deviation of the experimental data from the theoretical trend is attributed to the differences in protrusion edge sharpness and material surface properties (i.e., θ) for different textured surfaces. In addition, we found that when the texture size is on the order of a few nanometers,^13,16,19 the estimated τ is on the order of 10⁻¹¹ J/m, which is very close to the agreed magnitudes of τ_intrinsic.⁴¹ This indicates that pinning effects on these surfaces are very small or even negligible (i.e., p ∼ 0). On the other hand, as the texture size increases, the magnitudes of τ increase and can reach as high as the order of 10⁻⁹ J/m when r ∼ 100 nm. The large magnitudes of τ cannot be solely explained by the intrinsic line tension, which indicates the existence of pinning on these superhydrophobic surfaces (i.e., p > 0). This further reinforces that the apparent contact angles on these surfaces are not the most stable equilibrium values, which partially explained the discrepancy between the experimentally determined values and the theoretical predictions obtained by the classical Cassie–Baxter equation. This observation is in accord with a recent experimental study, which showed that the pinning effect plays an important role on superhydrophobic surfaces.⁴⁹

Figure 2.

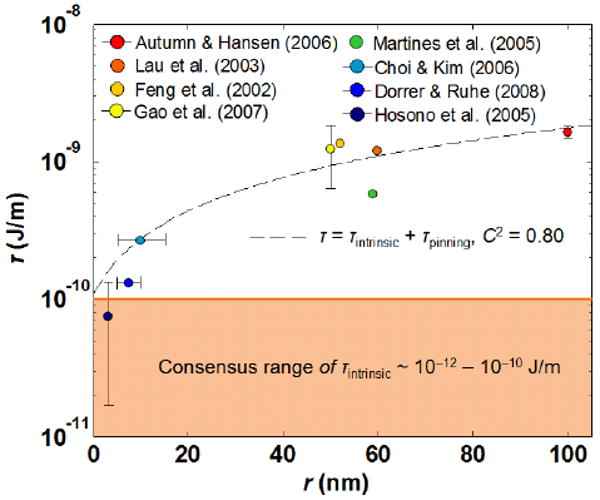
Semilog plot showing the dependence of line tension magnitude on protrusion radius of super/ultrahydrophobic surfaces with cylindrical-like textures. Line tension values are evaluated based on the reported upper limit of water apparent contact angles. The experimental trend can be approximated by the relationship τ = τ_intrinsic + τ_pinning with τ_intrinsic = 1 ×10⁻¹⁰ J/m, p = 0.23, and γ_LV of water = 73 × 10⁻³ J/m² (n = 8, C² = 0.80). The use of the proposed relationship is justified because the maximum characteristic length of protrusion presented in the experimental data (i.e., ∼100 nm) is much less than the capillary length of water (i.e., ∼2 mm). These data are complied from refs 4,¹⁰,¹²–¹⁴,¹⁶, ¹⁹,³⁰ and are tabulated in Supporting Information.

With the new quantitative relationship of τ, one can further comment on how the surface hydrophobicity varies with the texture size using eq 2 (Figure 3). It can be shown that when θ* is approaching 180°, the radius of the protrusion is approaching a limiting physical length scale, r_uh, which can be expressed as,

Figure 3.

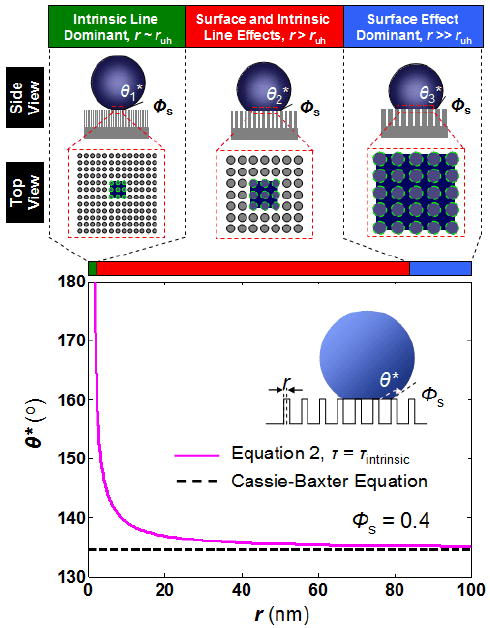
Influence of surface texture size on the apparent equilibrium contact angle of a water droplet. When the texture size is very close to r_uh, the surface will be rendered ultrahydrophobic due to the dominance of the line tension effect (intrinsic line dominant region). A textured surface with a high solid fraction can render a surface superhydrophobic when the texture size is on the order of r_uh (surface and intrinsic line effects, red solid line, Φ_s = 0.4). This is in contrast to the Cassie–Baxter theory where superhydrophobic surface cannot be achieved by high solid fraction (i.e., black dotted line, Φ_s = 0.4). Notice that when r ≫ r_uh, the apparent equilibrium contact angle predicted by eq 2 approaches that of the Cassie–Baxter equation (surface effect dominant region). The parameters used for eq 2 are τ_intrinsic = 5×10⁻¹¹ J/m, γ_LV of water = 73 × 10⁻³ J/m², and θ = 105°, and p = 0.

$$r_{\text{uh}}=\left(\frac{2}{1+cos\theta -2p}\right)\cdot \frac{{\tau }_{\text{intrinisc}}}{{\gamma }_{\text{LV}}}$$ (3)

Notice that this length scale includes the contribution from both τ_intrinsic and τ_pinning (i.e., p). In particular, when the pinning effect is small or negligible (i.e., 0 ≤ p < (1+cosθ)/2), ultrahydrophobicity is achieved when r ∼ r_uh. With τ_intrinsic ∼ 10⁻¹¹ J/m, γ_LV of water ∼ 73 × 10³ J/m², and p ∼ 0.23, r_uh is on the order of 1 nm. In this regime, Φ_s is not an important parameter to dictate ultrahydrophobicity, provided that the droplet is in an ideal Cassie regime. This can be illustrated by two recent artificial surfaces fabricated by Choi and Kim (r ∼5–15 nm, Φ_s ∼0.01),¹⁶ and Dorrer and Rühe (r ∼5–10 nm, Φ_s ∼1 × 10⁻⁴),¹⁹ whose Φ_s value differs by ∼2 orders of magnitude, yet both surfaces exhibited a similar degree of ultrahydrophobicity. In addition, r_uh is a weak function to the intrinsic material surface properties, θ, as compared to τ_intrinsic and γ_LV, when p is approaching zero. This implies that ultrahydrophobic surfaces could be made from a variety of materials under the condition that the droplet remains in an ideal Cassie regime. For example, Hosono et al. have recently demonstrated the use of a weakly hydrophilic material (i.e., θ = 75.2° ± 6.6°) to create an ultrahydrophobic surface (r ∼ 3 nm, Φ_s ∼6.12 ×10⁻⁴).¹³

When r is approaching r_uh, surface hydrophobicity increases due to the intrinsic line tension. In this regime, small structures (i.e., small r) can impart superhydrophobicity even for a high solid fraction of textures (i.e., large Φ_s). It can be shown that small intrinsic line tension magnitude (i.e., ∼10⁻¹¹ J/m) can influence macroscopic wetting of surfaces with texture sizes up to 50 nm in the lateral dimension (Figure 3). In the extreme case where r ≫ r_uh, the influence of intrinsic line tension becomes negligible and the most stable apparent equilibrium contact angle approaches that defined by the Cassie–Baxter equation. Deviation of the apparent contact angles from the most stable equilibrium value is attributed to the pinning effect (i.e., τ_pinning), which is experimentally demonstrated by Öner and McCarthy,⁹ Tujeta et al.,¹⁸ and Kurogi et al.⁴⁹

Conclusions

In summary, we show that physical texture size is the dominant parameter in determining surface hydrophobicity when the texture dimensions are on the order of τ_intrinsic/γ_LV (i.e., r_uh). The new governing equation provides a theoretical groundwork that justifies the use of nanoscopic textures (i.e., order of 1–10 nm) to render a surface ultrahydrophobic. An important implication from our study is that, by using surface textures with sizes on the order of 1–10 nm, the surface hydrophobicity can be further enhanced due to the intrinsic line tension, provided that an ideal Cassie regime is satisfied. In addition, our quantitative analysis indicates that the effect of pinning reduces with the texture size. This observation may provide additional physical insight into why nanoscopic textures are required by natural superhydrophobic surfaces to achieve high surface hydrophobicity, which is advantageous in maintaining their water-repellent capabilities.