Motor-Substrate Interactions in Mycoplasma Motility Explains Non-Arrhenius Temperature Dependence

Abstract

Mycoplasmas exhibit a novel, substrate-dependent gliding motility that is driven by ∼400 “leg” proteins. The legs interact with the substrate and transmit the forces generated by an assembly of ATPase motors. The velocity of the cell increases linearly by nearly 10-fold over a narrow temperature range of 10–40°C. This corresponds to an Arrhenius factor that decreases from ∼45 k_BT at 10°C to ∼10 k_BT at 40°C. On the other hand, load-velocity curves at different temperatures extrapolate to nearly the same stall force, suggesting a temperature-insensitive force-generation mechanism near stall. In this article, we propose a leg-substrate interaction mechanism that explains the intriguing temperature sensitivity of this motility. The large Arrhenius factor at low temperature comes about from the addition of many smaller energy barriers arising from many substrate-binding sites at the distal end of the leg protein. The Arrhenius dependence attenuates at high temperature due to two factors: 1), the reduced effective multiplicity of energy barriers intrinsic to the multiple-site binding mechanism; and 2), the temperature-sensitive weakly facilitated leg release that curtails the power stroke. The model suggests an explanation for the similar steep, sub-Arrhenius temperature-velocity curves observed in many molecular motors, such as kinesin and myosin, wherein the temperature behavior is dominated not by the catalytic biochemistry, but by the motor-substrate interaction.

Introduction

Mycoplasmas are a genus of wall-less bacteria with compact genomes that may have arisen as a result of retrograde evolution (1). They are the smallest known free-living, self-replicating organisms. Despite the loss of many biological functions, mycoplasmas demonstrate a novel gliding motility on solid substrates, such as glass, plastic, and surface of epithelial cells (2–4). Their locomotion is always in the direction of a characteristic membrane protrusion at one pole of the cell (the “nose”) (5–8). The mechanism of this motility is novel since the Mycoplasma genome contains no homologs to genes associated with known mechanisms of bacterial motility (9–12).

The motility studies are carried out mainly on the fastest gliding species, Mycoplasma mobile. Under lab conditions, M. mobile glides smoothly and continuously on glass surface with velocities of 2.0–4.5 μm/s, or 3–7 body lengths/s (13). The energy source is ATP hydrolysis (14–16). Recent experiments reveal a complicated motility organelle in its nose (17). The core of the organelle consists of a dock structure fixed at the distal end of the nose, and dozens of filaments extending radially from the dock. These filaments anchor ∼400 single protein “legs” that protrude through the cell membrane and interact with the substrate (Fig. 1) (18–22). Since the leg is the best studied protein in the complicated organelle, our model focuses on how these legs harness the forces generated by the ATPase motors to drive the motion of the cell.

Figure 1.

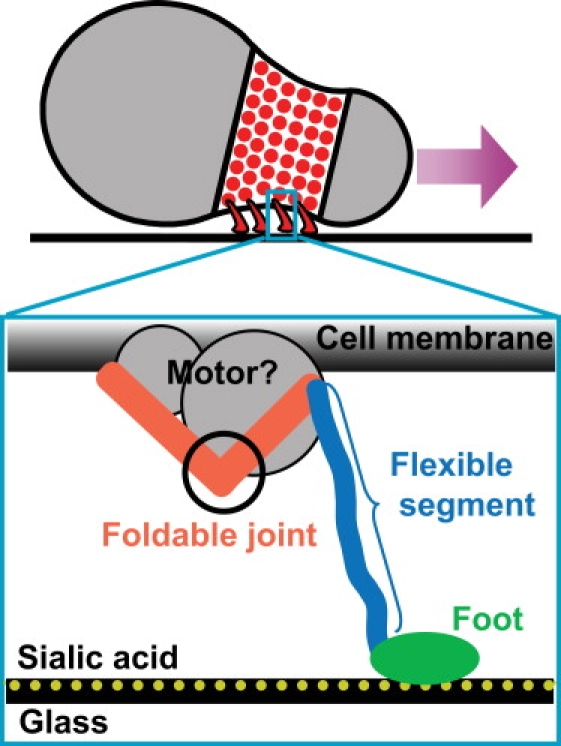
Motility apparatus of M. mobile. Four-hundred leg proteins are located at the neck of the M. mobile cell. Each leg assumes a music-note-like shape (zoom-in view), with two arms at the proximal end, and a long flexible segment (blue) with a foot (green) that interacts with the substrate.

M. mobile shows intriguing velocity changes with temperature and load force. The velocity increases almost linearly by ∼10-fold over a narrow temperature range from 10°C to 40°C (see Fig. 3 A) (23). Translated onto a 1/T ∼ logV plot (see circles in Fig. 3 B), these data correspond to an Arrhenius factor that decreases from ∼45 k_BT at 10°C to ∼10 k_BT at 40°C. On the other hand, the velocity decreases nearly linearly with increasing load force, but the stall force extrapolates to ∼25 pN at different temperatures (compare to Fig. 4 in Miyata et al. (23)). Cells attached to micro-beads trapped by optical tweezers also stall when pulled by a force of ∼25 pN (23). These data suggest that the force-generation step is insensitive to temperature near stall loads.

Figure 3.

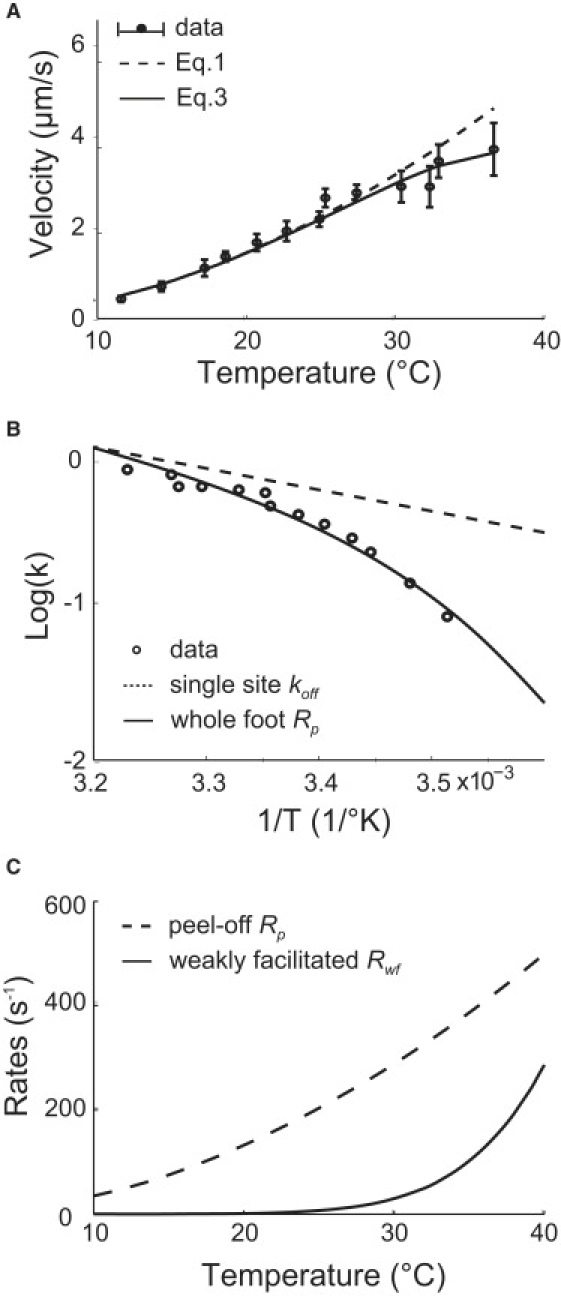
Temperature-velocity results. (A) Temperature versus velocity curve. Circles and error bars show the experiment data (taken from Miyata et al. (23)); the dashed line is the fitting of the model without weakly facilitated foot release during the power stroke using Eq. 1; the solid line shows the result with weakly facilitated foot release during power stroke using Eq. 3. The effect of weakly facilitated foot release becomes significant at high temperatures, and corrects the deviation from the data. (B) The Arrhenius plots of the foot rates and of the data. For comparison, the rates have been multiplied by corresponding constants to level the logarithm plots at the left end. The whole foot peel-off rate, R_p, has a much larger Arrhenius factor than the off-rate of a single site does because of the multiplying effect shown in Eq. 2. Also, the Arrhenius factor of R_p decreases as temperature increases. (C) The peel-off rate R_p and weakly facilitated release rate R_wf. The weakly facilitated rate becomes significant at ∼25°C, resulting in the attenuation of velocity at high temperatures.

In this article, we propose a leg-substrate interaction mechanism to explain the non-Arrhenius temperature dependence of Mycoplasma motility. In this mechanism, the release of the leg from the substrate is the major temperature-sensitive factor. Soo and Theriot (24) suggested in their model for Listeria motility that the large Arrhenius factor for the cell velocity is caused by the cooperative breaking-off of multiple binding sites so that the Arrhenius factors of single sites add. Our model goes further and explains the decrease in the Arrhenius factor as temperature rises, i.e., the sub-Arrhenius relationship between temperature and velocity. The model can be generalized to explain similar temperature sensitivity observed in many “walking” molecular motors such as kinesin and myosin (25,26). This theory reveals the motor-substrate interaction, especially the unbinding process, as the dominant factor affected by temperature, albeit not in a simple Arrhenius fashion.

Model and Results

In the following sections, we first lay down the framework for the motility process and the basic assumptions used in our model. After that, we go into the details of the leg-substrate interaction. In particular, we show that the multiple substrate-binding sites on the leg contribute to the steep, sub-Arrhenius temperature-velocity curve. In addition, we rectify the remaining deviation of the results at high temperatures by the weakly facilitated foot release during the power stroke. Finally, we show that the resultant load-velocity curve fits with the experimental data and explains the dynamical trajectories observed in optically trapped Mycoplasma cells, as well as the temperature-insensitive stall force.

Leg cycle

The sequence and geometric shape of the leg protein in Mycoplasma has been deduced from electron microscopy studies. The protein looks like a music note (Fig. 1; see also Fig. 9 in Adan-Kubo et al. (21)). The two short arms at the proximal end assume an open or a closed conformation, suggesting that the opening and closing motion is driven by the ATPase motor (16). The distal end bulges into a “foot” that interacts with the negatively charged substrate through multiple basic amino acids. The proximal arms and the foot are connected by a long segment. Atomic-force microscopy experiments suggest that this long segment is quite flexible (27), so that its mechanical property resembles that of a rope, i.e., exerting much less resistance to being compressed than being stretched.

Based on the structure of the leg protein and the proposed motility mechanism in Miyata (28), we modeled the mechanochemical cycle of a single leg as shown in Fig. 2 A.

Figure 2.

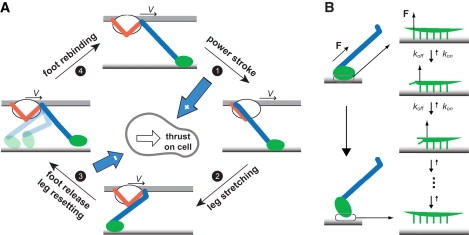
Mechanochemical model of a single leg protein. (A) Mechanochemical cycle of the leg. The leg starts in the front conformation with the foot bound to the substrate. As ATP zippers into the catalytic site, the motor carries out a power stroke, pulling the cell forward. After the power stroke, the cell continues moving forward at constant velocity V, driven by the collective action of the other legs. The foot lags behind until the long segment is once again in tension. Acting on one end of the foot, the tension helps peel the foot off the substrate. The system must wait for the foot to release from the substrate so that the leg can reset to the front conformation, allowing the motor to bind ATP once again. The cycle repeats as the foot rebinds to the substrate. ATP binding and foot rebinding are assumed to happen very fast, thus not resolved in the analysis. During the cycle, the power stroke applies a positive force on the cell body, and the foot, tethered beyond its backward restressed position, applies a negative force (blue arrows). (B) Mechanism of foot peeling. The foot interacts with the sialic acids in the substrate through multiple binding sites. The bonds are shown by green projections in the zoom-in view on the right. When the stretched intermediate segment pulls on the foot from one end, most of the tension is exerted on the frontmost bond and thus significantly facilitates its unbinding, analogous to peeling-off a Velcro strip. In the idealized case, the bonds break off sequentially, forming a Markov process as shown in the sequence of events on the right. The Markov process gives an average peel-off rate of the foot as in Eq. 2.

The mechanochemical cycle begins with the leg in the front position and the foot bound to the substrate. When ATP loads into the motor, the motor carries out a power stroke and pulls on the foot. This process exerts a forward force on the cell body. After the power stroke, the cell continues moving forward, driven by the collective work of the other legs. The foot lags behind. The long segment becomes slack and exerts no force until the foot reaches the backward position and restretches the long segment. The long segment pulls the foot off the substrate. Then the leg resets to the front position, the foot rebinds to the substrate, and the cycle repeats. We impose the kinematic constraint that the cell moves relative to the substrate with a constant velocity V. This simplifies the mathematical analysis, and is justified by the large number of legs and consequent small fluctuations in the velocity of the cell.

In such a system with many degrees of freedom, it is natural to have other pathways on the complicated energy landscape. What we proposed above is the main pathway that most legs follow. For this cycle to dominate over the other pathways, the following assumptions must hold:

• Assumption 1.

  The hinge connecting the proximal arm and the long segment is weakly elastic, with its rest state in the front position. This provides the resetting force for the leg.

• Assumption 2.

  The motor can bind ATP only after the leg fully resets to the front position. It can be explained by hidden coordinates for the motor (see Appendix). This assumption, together with Assumption 3, ensures that the power stroke always starts from the front position. This is for analytical convenience, and does not change the essential features of the model.

• Assumption 3.

  The foot only rebinds to the substrate after it fully resets to the front. We picture the long segment behaving like a Venetian blind: the long segment kinks easily under a backward force and the kink propagates down toward the foot while the segment resets to the front position (leftmost panel of Fig. 2 A). During resetting, the kink keeps the foot in an unfavorable angle to the substrate, preventing its binding until the resetting completes. During the power stroke, however, the segment is unbent because it is under tension.

• Assumption 4.

  The foot releases more easily when it is pulled forward after the power stroke (step 3 in Fig. 2 A). This is because the long segment is attached to the posterior end of the foot so that it imposes a peeling force when it pulls the foot forward, as shown in Fig. 2 B. This mechanical asymmetry is necessary for net forward motion.

The velocity of the cell is computed from the force balance on the legs. Since inertial forces are negligible at such low Reynolds number, the load force and hydrodynamic-drag force on the cell body is equal to the total force generated by the motility organelle. The estimated hydrodynamic drag on the micron-sized cell body moving with a velocity of ∼1 μm/s is ∼10⁻² pN, much smaller than the scale of the external load force applied in the experiments; therefore, it can be neglected. The motility organelle generates force mainly by two steps in the leg cycle: the power stroke generates a positive force and the foot tethered beyond the backward restressed position imposes a negative force. During the restretching and resetting steps, the only force is the weak elastic resetting force, which we treat as negligibly small. Intuitively, the force balance at all times ensures the balance of the ensemble average force; and the latter is equivalent to the balance of force impulses. Thus, the force balance can be conveniently expressed as an impulse balance:

$$Loadforce\times cycleperiod=\#legs\times \left(impulsefrompowerstroke-impulsefromtetheredfoot\right)\text{.}$$

In Section III of the Supporting Material, we derive the full version of the force balance equation from the transport equations for the density of feet. These equations can be reduced to the above equation when we neglect the hydrodynamic drag forces and consider the high velocity case.

At zero load, the two impulses in the parentheses cancel, leading to Eq. 1. Here V is the velocity of the cell, f_m is the motor force, λ is the power stroke length, κ is the elastic constant of the intermediate segment, and R_p is the peel-off rate of the foot. The computation of R_p leads to the most important conclusion of this article and will be discussed in detail in the following section. On the left-hand side of Eq. 1, λ/V is the mean residence time of the foot in the power stroke. Therefore, the mean impulse delivered by a single foot in one power stroke is f_mλ/V. On the right-hand side, V/R_p is the average stretching of foot from the backward restressed position, and thus, κV/R_p is the average force acting on the backward foot. Since the lifetime of backward bound state is 1/R_p, the impulse delivered per foot in this part of the cycle is (κV/R_p) × (1/R_p) = κV/R_p²,

$$f_{\text{m}}\frac{\lambda }{V}=\frac{\kappa V}{R_{\text{p}}^2}\Rightarrow V=\sqrt{\frac{f_{\text{m}}\lambda }{\kappa }}{R}_{\text{p}}\text{.}$$ (1)

Equation 1 shows that the unloaded velocity is proportional to the peel-off rate of the foot. The temperature dependence of the velocity follows that of the peel-off rate, as we show in the following that terms under the square-root are approximately temperature-invariant. The power stroke length, λ, is determined by the geometry of the motor and the leg, and should not change significantly with temperature. The motor force depends on temperature approximately linearly, i.e., f_m ≃ ΔG/λ = (ΔH − TΔS)/λ; it changes by ∼10% over the temperature range of 10°C ∼40°C, far from enough to account for the 10-fold increase in velocity. The elastic constant of the stretched leg, κ, depends on the configuration of the intermediate segment. Using the same argument for the motor force, the elastic constant resulting from the entropic part of the spring is a linear function of temperature (29), and does not change much in the relevant temperature range. The enthalpic part of the spring is usually attributed to chemical bonds. Since the enthalpy of a chemical bond is generally insensitive to temperature, so is the resultant spring constant.

In the next section we will derive the temperature dependence of the foot peel-off rate with an embedded submodel of the foot-substrate interaction. The submodel explains the steep, sub-Arrhenius temperature-velocity curve, except for some deviation in the high temperature regime.

Foot-substrate interaction

We now consider the foot-substrate interaction in more detail. This is the core part of the model, which explains the steep, sub-Arrhenius temperature-velocity curve.

The foot anchors to the negatively charged sialic acids in the substrate (30). The C-terminal domain of the leg protein, which constitutes the bottom part of the foot, contains multiple positively charged amino acids (18 Arg, 21 Lys). It is likely that specific binding sites for sialic acid form around these basic amino acids. Previous studies on the sialoadhesin receptor shows that the sialic acid binding site consists of two key amino acids with positive charges (31). This gives an estimate of <20 binding sites on the foot of Mycoplasma, based on which we used 10 in our model. That is, the foot is modeled as an anchoring strip with 10 sites that holds on to the substrate.

The asymmetric geometry of the leg protein suggests that the foot releases from the substrate more easily when pulled forward instead of backward. A backward pulling force, as that during the power stroke, is distributed almost equally among all the binding sites. A forward force, however, is concentrated mostly on the rearmost site, largely facilitating its unbinding. After the rearmost site unbinds, the next one undertakes most of the external force and unbinds quickly; and it goes on until all sites unbind. This process is analogous to peeling off a Velcro strip from one end to the other—by contrast it is much harder to rip off the Velcro by exerting an evenly distributed force on it.

The peeling-off of the foot can be modeled by a Markov process as shown in Fig. 2 B. Since the rearmost binding site is much more likely to unbind, the unbinding of different sites takes place approximately sequentially. Let Q be the number of binding sites. The corresponding Markov process consists of Q+1 states, each indicating the order of the current rearmost bound site, plus the “all-off” state:

$$Q\underset{\underset{k_{\text{on}}}{\leftharpoondown }}{\overset{k_{\text{off}}}{\rightharpoonup }}Q-1\underset{\underset{k_{\text{on}}}{\leftharpoondown }}{\overset{k_{\text{off}}}{\rightharpoonup }}\cdots \underset{\underset{k_{\text{on}}}{\leftharpoondown }}{\overset{k_{\text{off}}}{\rightharpoonup }}1\underset{\underset{k_{\text{on}}}{\leftharpoondown }}{\overset{k_{\text{off}}}{\rightharpoonup }}0\left(\text{all-off}\right)\text{.}$$

If the on- and off-rates of all binding sites are identical, the derivation presented in Section I of the Supporting Material gives the peel-off rate of the whole foot as

$$R_{\text{p}}=k_{\text{off}}\times \frac{{\left(1-K\right)}^2}{Q-\left(Q+1\right)K+K^{\text{Q}+1}},$$ (2)

where K = k_on/k_off is the binding constant of a single site. As temperature increases, the enhanced thermal fluctuations facilitates the unbinding, thus decreasing the binding constant, K. Equation 2 satisfies the following properties:

$$\text{Low}\text{temperature}\text{limit}:\Rightarrow R_{\text{p}}\to k_{\text{off}}/K^{\text{Q}-1},$$

$$\text{High}\text{temperature}\text{limit}:\Rightarrow R_{\text{p}}\to k_{\text{off}}/Q\text{.}$$

If the binding constant, K, depends on temperature in an Arrhenius way, then in the low temperature limit, the Arrhenius factor of the foot peel-off rate, R_p, is approximately the Arrhenius factor of K multiplied by the number of sites. This multiplicity effect, however, attenuates as temperature increases; eventually, the effective Arrhenius factor tends to approximately the Arrhenius factor of K at the high temperature limit.

The feature of the model discussed so far leads to the steep, yet sub-Arrhenius temperature dependence of the velocity (dashed line in Fig. 3 A). Data fitting gives the values of the single site rates, k_on and k_off, as listed in Table 1. Fig. 3 B compares the Arrhenius plot of the single-site unbinding rate, the whole-foot release rate, and the temperature-velocity data. Each site bears a factor of 10 k_BT (Table 1). However, the Arrhenius factor of the whole-foot rate amounts to ∼45 k_BT at 10°C, and attenuates to ∼10 k_BT at 40°C.

Table 1.

List of parameters

Parameters	Value	Physical meaning	Source/reason
N	100	Number of legs.	Out of a total of 400 legs, one-quarter face the substrate.
Q	10	Number of binding sites on each foot.	Structural information: number of charges on the foot.
fm	0.39 pN	Motor force.	Fitting Eqs.1 and 2 with T-V data.
λ	28 nm	Power stroke length.	Structure of leg protein: 90° conformational change between two arms of 20 nm.
κ	80 pN/μm	Elastic constant of intermediate segment.	Physiological range.
kon, k′on	2.9 × 103 s−1	Binding rate of single site.	Fitting Eqs.1 and 2 with T-V data, assuming that the on-rates are not affected by external force.
koff	4.2 × 103 s−1(10.6 kBT)∗	Peel-off rate of single site (and its Arrhenius factor).	Fitting Eqs. 1 and 2 with T-V data.
k′off	1.9 × 103 s−1(16.8 kBT)∗	Weakly facilitated release rate of single site (and its Arrhenius factor).	Fitting Eqs. 1 and 2 with T-V data.

^∗Rates are listed as their values at the reference temperature 22.5°C.

Weakly facilitated foot release during the power stroke rectifies the high-temperature curve

During the power stroke, the foot may also release from substrate. This foot release rate is much smaller than the peel-off rate at low temperature, but becomes significant as temperature increases. In this case, all the binding sites share the burden of the motor force. With much weaker facilitation than in the peel-off case, the energy barrier to break the binding of a site remains high and thus the unbinding rate bears a much larger Arrhenius factor. As a consequence, the overall foot release rate increases acutely with temperature (Fig. 3 C).

The foot release curtails the power stroke, and consequently reduces the velocity. This is shown by the velocity dependence in Eq. 3. Here R_wf denotes the weakly facilitated foot release rate:

$$f_{\text{m}}\frac{1-\exp \left(-R_{\text{wf}}\lambda /V\right)}{R_{\text{wf}}}=\frac{\kappa V}{R_{\text{p}}^2}\Rightarrow V=\frac{1-\exp \left(-R_{\text{wf}}\lambda /V\right)}{R_{\text{wf}}}\frac{f_{\text{m}}}{\kappa }{R}_{\text{p}}^2\text{.}$$ (3)

The fractional term on the left-hand side of Eq. 3 stands for the average duration of the effective power stroke. It is computed from

$${\int }_0^{\lambda /\text{V}}tf\left(t;R_{\text{wf}}\right)dt+{\int }_{\lambda /\text{V}}^{\mathrm{\infty }}f\left(t;R_{\text{wf}}\right)\lambda /Vdt,$$

where f(t; R_wf) is the probability density function of the exponential distribution. Equation 3 tends to Eq. 1 in the limit R_wf → 0, i.e., when the weakly facilitated foot release rate is negligibly small. Because the weakly facilitated rate increases sharply with increasing temperature, its effect on velocity dominates at high temperature. This is the other feature of the model that rectifies the temperature-velocity curve at high temperatures (solid line in Fig. 3 A).

The weakly facilitated foot release also corresponds to a Markov process. The Markov states stand for the number of binding sites currently bound. The binding sites do not have to unbind in a certain order, so the forward rate from state i to i−1 equals ik′_off to account for the fact that every bound site has an equal chance to unbind. Similarly the backward rate from state i to i+1 equals (Q − i)k′_on,

$$Q\underset{k_{\text{on}}^{\prime }}{\overset{Q{k}_{\text{off}}^{\prime }}{\rightleftharpoons }}Q-1\underset{2k_{\text{on}}^{\prime }}{\overset{(Q-1)k_{\text{off}}^{\prime }}{\rightleftharpoons }}\cdots \underset{(Q-1)k_{\text{on}}^{\prime }}{\overset{2k_{\text{off}}^{\prime }}{\rightleftharpoons }}1\underset{Q{k}_{\text{on}}^{\prime }}{\overset{k_{\text{off}}^{\prime }}{\rightleftharpoons }}0\left(\text{all-off}\right)\text{.}$$

With the derivation given in Section II of the Supporting Material, we obtain the weakly facilitated foot release rate as Eq. 4. It is computed with k′_on and k′_off, given in Table 1,

$$R_{\text{wf}}=\frac{Q{k}_{\text{on}}^{\prime }}{{\left(1+k_{\text{on}}^{\prime }/k_{\text{off}}^{\prime }\right)}^{\text{Q}}-1}\text{.}$$ (4)

As in Eq. 2, we see that the exponential term in Eq. 4 also brings about the multiplicity of the Arrhenius factor for the single-site binding constant.

This newly introduced detail of the model reduces the calculated velocity significantly for temperatures above 25°C (solid line in Fig. 3 A). With much smaller facilitating force, the energy barrier associated with the unbinding of each site is larger, at 17 k_BT (Table 1). Consequently, the weakly facilitated rate rises sharply, starting at ∼25°C (Fig. 3 C). Nevertheless, it is smaller than the peel-off rate because of less facilitation.

The load-velocity curve explains the dynamical trajectory

In this section we show an interesting hysteresis behavior in the load-velocity curve at low velocities. This leads to an explanation for the dynamical trajectory observed in optical trap experiments.

The calculated load-velocity curve of the model fits with the experiment data (Fig. 4 A). Our calculation also extends to the low velocity and negative velocity regime, beyond the range of the data. The curve displays hysteresis: it turns around at a small positive velocity that depends on temperature, and returns in the negative velocity regime. The branching in the positive regime takes place because the foot can spontaneously release from the substrate at a small, yet finite rate during the restretching step. The spontaneous foot release is a natural consequence of thermal fluctuations. Without any external help, the rate of spontaneous release is even smaller than that of the weakly facilitated release. At large cell velocities, the foot translates backward fast enough to restretch the leg, before which the spontaneous release almost never has a chance to occur. Near stall (i.e., zero velocity), however, the spontaneous foot release has to be taken into account. It circumvents the peel-off of the foot and the negative impulse associated with it. This enhanced model is formulated via the transport equations in Section III of the Supporting Material. The solution gives the load-velocity curve in Fig. 4 A.

Figure 4.

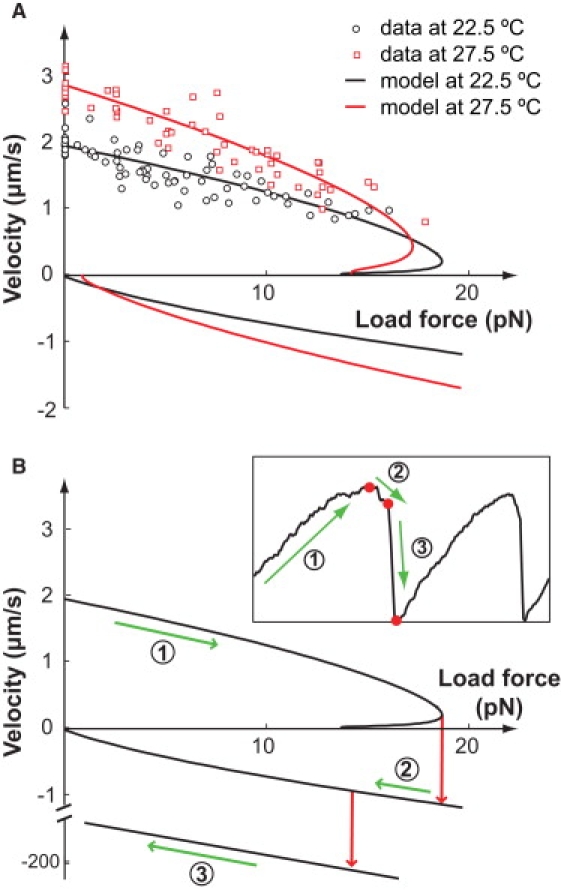
Load-velocity curve explains the dynamical behavior in the laser trap experiments. (A) Load force versus velocity curve. The model results are computed beyond the velocity regime measured in the experiments. Hysteresis is predicted by the model. (B) Mapping of the dynamical trajectory onto the load-velocity curve. The middle branch of the load-velocity curve is unstable. The straight line added at the bottom of the plot shows the hydrodynamic load-velocity curve, i.e., when the cell is off the substrate. The dynamical trajectory measured from an optically trapped Mycoplasma is shown in the inset (taken from Miyata et al. (23)). The labeled green arrows along the load-velocity curve and the dynamic trajectory show, correspondingly, the three motility phases of the cell: 1), forward; 2), backward; and 3), free after detachment. The red arrows on the load-velocity curve and the red dots on the trajectory indicate corresponding transitions between the three phases. This branching load-velocity curve explains the forward-to-backward transition in the dynamical trajectory. However, the backward-to-break-off transition cannot be explained without further experimental information.

The hysteresis in the load-velocity curve explains the dynamical trajectory observed in the experiment, in which the Mycoplasma is attached to an optically trapped bead. This experiment captures the slowing down of the motion to near-stall (Fig. 5 in Miyata et al. (23); also shown in the inset of Fig. 4 B). At first, the cell drags the trapped bead away from the center of the laser beam, thus increasing the load force experienced (the laser trap is well approximated by a quadratic potential, i.e., a linear spring). The cell slows until it reaches the position in the trap that generates a load force ∼20 pN. At this force, the cell begins to slide backward, and eventually breaks off from the substrate. Then the cell is quickly drawn back to the center of the trap where it reattaches, and the cycle repeats.

The corresponding trajectory is mapped out on the load-velocity curve, shown in Fig. 4 B. The cell first traces down the upper branch of the load-velocity curve until it reaches the nose. It cannot follow the unstable middle branch—otherwise it would have a positive velocity yet move in the backward direction with decreasing load force. Thus, it must jump to the lower branch of the curve. On this branch, the cell begins to slide back (negative velocity). However, this does not persist long before the cell detaches from the substrate. Now the cell is quickly drawn back to the center of the trap with a much larger velocity determined by its hydrodynamic drag.

The stall force changes with temperature much less than the unloaded velocity. At very low velocity, the feet hardly complete the power stroke before the weakly facilitated release. For the same reason, the peel-off is interrupted by the spontaneous foot release. Therefore, the average force contributed by a foot in an average cycle is approximately the motor force multiplied by the fraction of cycle period spent in the power stroke. The motor force is insensitive to temperature, as discussed previously. The fraction of power stroke time apparently does not change too much with temperature (solid line in Fig. 5 B), either, nor does the stall force.

Figure 5.

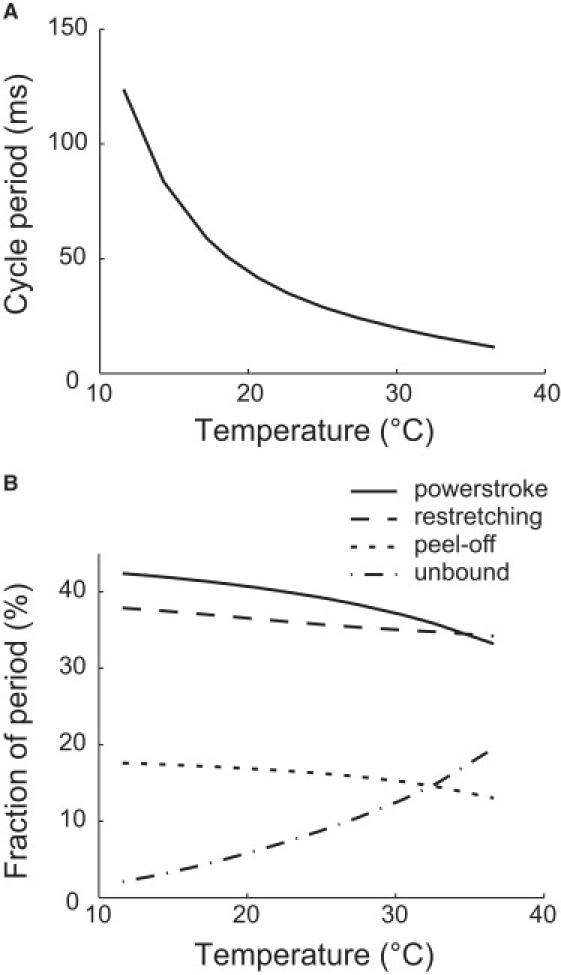
Cycle period and residence times of each stage change with temperature. (A) The cycle period decreases with temperature, ranging between 10 and ∼10² ms in the relevant temperature range. (B) Temperature affects the durations of the power stroke (solid), restretching (dashed), peel-off (dotted), and the unbound states (dash-and-dotted). These results are computed from Eq. S28 in the Supporting Material.

However, the stall force predicted by the model is somewhat smaller than the stall force measured by the optical trap experiment. This may be due to the approximation that, during the peel-off, the unbinding rates of all the binding sites are assumed identical. In reality, the unbinding rates probably increase with the order of sites because the tension of the leg increases with time. However, without further information about the elasticity and geometry of the leg, it is fruitless to pursue the model beyond its current stage.

Discussion

We have constructed a minimal mechanochemical model of the Mycoplasma motility apparatus based on current knowledge. The model is able to explain the interesting biophysical properties of the motility, especially the steep, sub-Arrhenius dependence of velocity on temperature. The model assumes the simplest coupling among the motor, intermediate segment, and foot, and no coupling between legs. Each leg simply rows forward and backward which, if completely symmetric, would not produce any net forward motion. Net forward motion is guaranteed by the asymmetric geometry of the leg, which causes the foot to release from the substrate more easily when peeled from the back. The high temperature sensitivity of the peel-off rate results from the multiplicity of the single-site Arrhenius factor. The factor decreases as temperature rises, contributing to the sub-Arrhenius behavior of the temperature-velocity curve. Furthermore, the weakly facilitated foot release during the power stroke curtails the positive impulses and reduces the velocity at high temperatures. Finally, the dynamical process measured in laser trap experiments is explained qualitatively by the resultant load-velocity curve.

Certain biological parameters are estimated through the model. The binding and release rates of single binding site directly result from the fitting to the experimental data. They are all ∼10³ Hertz (Table 1). The peel-off rate is 2∼3 times as large as the weakly facilitated release rate. The average cycle period of the leg in the unloaded cell is approximately 10∼10² ms, which shortens with increasing temperature (Fig. 5 A). The power stroke and the subsequent leg restretching each takes ∼40% of the period in average (Fig. 5 B). Peeling off the foot takes ∼15% of the period. For the rest of the cycle period, the foot is unbound. Notice that the fraction of unbound time increases significantly with temperature, which helps explain that the cell easily detaches from the substrate at high temperatures. The cycle period also increases with increasing load force or decreasing velocity. When the cell approaches stall, the cycle is limited by the spontaneous release of the foot, and the cycle period tends to the reciprocal of that rate. The Stokes efficiency, estimated by F_LVτ/ΔG_ATP, is ∼10% for the optimal load; here, F_L is the load force and τ the cycle period. The above estimations fall in the proper biological range. Nevertheless, they are very rough, limited by the coarse-graining of the model.

The model also provides several predictions for experimental comparison. For example, the cell velocity peaks at a certain sialic acid density on the substrate (Fig. 6 A). This was shown by experiments changing the concentration of sialic acid used for coating the substrate (compare to Fig. 6 in (30)). Only qualitative comparison can be drawn at this moment, because we lack detailed information about the mechanism of foot binding as well as the relationship between sialic acid concentration in the coating medium and the sialic acid density finally presented on the surface of the substrate. We can also predict the effect of medium viscosity on the load-velocity curve (Fig. 6 B). Increasing the viscosity reduces the velocities for any given load force. In addition, the load-velocity appears more concave at higher medium viscosity. This change occurs because the resetting process is slowed at high viscosity and the hydrodynamic drag forces become more significant, compared with the other forces involved in the motility. Consequently, the cycle period is lengthened and the net force impulse provided per cycle is affected as well (compare to Eq. S28, Eq. S30, Eq. S33, and Eq. S34 in the Supporting Material).

Figure 6.

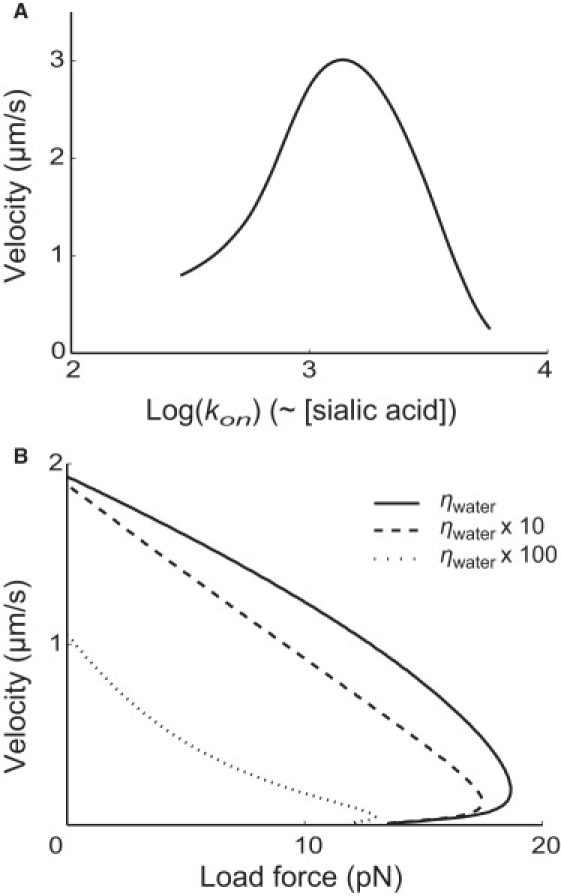
Predictions of the model. (A) The effect of sialic acid concentration on the cell velocity. The horizontal axis shows the logarithm of the single-site binding rate, which is directly related to the density of sialic acid on the substrate surface. The model predicts the existence of an optimal sialic acid density for Mycoplasma motility, to be compared with the experiment result presented in Fig. 6 of Nagai and Miyata (30). (B) The effect of viscosity on the load-velocity curve. The curves are computed for the mediums bearing the normal water viscosity (solid line), 10 times larger (dashed line), and 100 times larger (dotted line). The cell velocity decreases when viscosity increases. In addition, the load-velocity curve becomes more concave with larger viscosity.

Single molecule experiments on single legs are probably the best way to test the foot-substrate interaction mechanism proposed here. According to our model, the leg should break off from the substrate much easier under forward pulling force than it does under backward pulling force. Further structural information on the binding sites would also be useful in narrowing down the range of model parameters and estimating the energy barrier involved in the unbinding process.

The model for Mycoplasma motility can be generalized to other motility systems. Many walking molecular motors such as kinesin and myosin, show steep, sub-Arrhenius temperature-velocity curves (25,26,32–34). Even in rotary motors, like the Escherichia coli flagellar motor (35,36), the way that the stators push on the rotor is analogous to the Mycoplasma legs walking on the substrate. Unlike the intuitive considerations of the catalytic biochemistry, we proposed the motor-substrate interaction as the major factor to explain the temperature sensitivity. This theory can be more easily tested with experiments on molecular motors because there are more techniques to manipulate them.

Limited by the information on Mycoplasma motility, our model is quite coarse-grained with many approximations. The peel-off mechanism itself was derived with the approximation of identical off-rates for all binding sites. A refined model with more realistic description of the rates can probably fit the stall force better. Moreover, the model is built on the horizontal spatial coordinate only. The vertical components of the forces, however, probably play a critical role in the peel-off of the foot, and even the break-off of the whole cell. Adding such details requires a more refined model. However, without knowing the detailed molecular mechanism of the foot-substrate interaction, such elaboration is merely guesswork.

Appendix: Hidden Coordinates For The Motor

The molecular motor is a large protein, and so a complete atomic description of its motion requires a very high-dimensional configuration space: at least 3N-dimensional, where N is the number of atoms. Generally, the large-scale motions of proteins are dominated by a small number of modes. For example, we have simplified the motion of the motor to the opening and closing of the proximal part of the leg protein. By doing so, we are essentially projecting the high-dimensional periodic motion onto one single coordinate and treating it as a one-dimensional periodic oscillation. Although the resolved motor cycle appears to be moving forward and then backward along exactly the same trajectory, the hidden atomic degrees of freedom do not exactly retrace the same route. In particular, the second law of thermodynamics requires a loop in the force-displacement phase trajectory to account for the free energy consumption in the biochemical process. Such a loop is impossible when we simplify the motion to one dimension. We must include at least two configurational coordinates, say (z, θ), to form a cyclic loop in the (z, θ) plane. Therefore, the open conformation of the motor before the power stroke and the open conformation after the ADP release, although not distinguished in the model, are in general not equivalent. ATP can bind to the former conformation, but not the latter one. Instead of increasing the dimensionality of the model, we simply declare that ATP loading only happens after the leg fully resets to the front position.

Supporting Material

Three supplementary sections with one table, one figure, and 34 equations are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01466-0.