Figure 1.
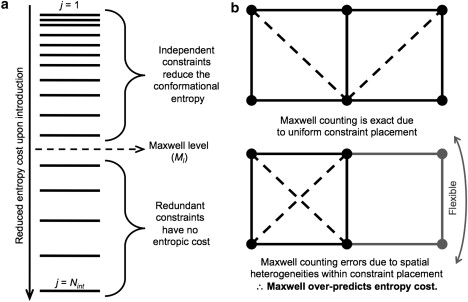
(a) Generic entropy spectrum. All interactions present in a network are rank-ordered by their entropy components (from top to bottom of the spectrum, j = 1 to Nint). A cutting line defines the Maxwell level, which defines the rigidity transition. Interactions ranked-ordered before the Maxwell level (i.e., j ≤ Ml) reduce Sconf, whereas interactions past it (i.e., j > Ml) do not. The type of interaction is not indicated in this schematic because sorting is based solely on entropy ranking. (b) The Maxwell counting approximation is explained by a simple edge-sharing quadrilateral in two-dimensions (rigid substructures are black, whereas flexible substructures are gray). In the top example, both quadrilaterals are isostatically rigid (meaning, rigid but no redundant constraints). In this case, two identical fluctuating interactions are present (shown as dashed lines), and each pays an entropic cost (e.g., a total cost of 2γ). Here, the entropy cost calculated by Maxwell equals the true network rigidity result due to uniformity. However, in the bottom example, the true entropy cost is only γ because one of the interactions is redundant. However, Maxwell assumes all interactions up to Ml are independent irrespective of their location in the network, which results in overprediction (again, 2γ) of the Sconf cost.
