Summary
A recent article in Acta Psychologica (“Picture-plane inversion leads to qualitative changes of face perception” by B. Rossion, 2008) criticized several aspects of an earlier paper of ours (Riesenhuber et al., “Face processing in humans is compatible with a simple shape-based model of vision”, Proc Biol Sci, 2004). We here address Rossion’s criticisms and correct some misunderstandings. To frame the discussion, we first review our previously presented computational model of face recognition in cortex (Jiang et al., “Evaluation of a shape-based model of human face discrimination using fMRI and behavioral techniques”, Neuron, 2006) that provides a concrete biologically plausible computational substrate for holistic coding, namely a neural representation learned for upright faces, in the spirit of the original simple-to-complex hierarchical model of vision by Hubel and Wiesel. We show that Rossion’s and others’ data support the model, and that there is actually a convergence of views on the mechanisms underlying face recognition, in particular regarding holistic processing.
Introduction
Faces are an object class of significant interest for many areas of cognitive neuroscience, including object recognition, decision making, social cognition, and perceptual learning. As with many other aspects of cognition, the effortlessness with which most of us perceive faces belies the complexity of the underlying neural processes. Indeed, the richness of behavioral phenomena associated with faces has stimulated much exciting research. Foremost among these behavioral phenomena is the so-called face inversion effect (Yin, 1969), FIE, referring to the observation that people are substantially worse at discriminating faces presented upside-down than right side-up, whereas inversion usually has less of an impact on the discrimination of objects from other classes. Subsequent research has established that this advantage for upright vs. inverted faces might be due to the fact that faces are processed “holistically”, i.e., that whole faces are processed more efficiently than their component parts (Tanaka & Farah, 1993)1.
Is Face Processing “Special”?
A key question and bone of contention has been whether quantitative differences in the recognition of inverted faces relative to upright faces and of isolated face parts relative to the same parts embedded in whole (upright) faces necessarily imply that there need be a qualitative difference in the way faces are processed relative to other objects (making faces “special”), or whether face perception can be seen as a particular case of “generic” object recognition, relying on the same kinds of neural mechanisms underlying the recognition also of non-face objects, but refined through extensive experience with a particular object class, namely faces.
One approach to answering this question is to assume that faces are indeed “special” and then try to define qualities that might make faces “special” relative to other object classes. For instance, faces differ from non-face objects in that they usually contain two eyes, a mouth, and a nose, and that there are regularities in how these parts are arranged, e.g., the eyes are usually above the mouth and the nose is in-between, giving rise to theories that face recognition may be based on recognizing individual face parts (usually called “features”, see footnote 1) and then computing their “configuration.” This raises the question of what the particular face parts are supposed to be and what should make up their “configuration.” While early studies (e.g., (Haig, 1984)) defined “features” as “eyes, mouth, and nose”, other studies have used more elaborate feature sets, e.g., by breaking up the eye “feature” into eyeball and eyebrow (Goffaux & Rossion, 2007). Correspondingly, “configuration” has been defined in a variety of ways, ranging from the simple (“the second order spatial configuration” between features (Carey & Diamond, 1986)) to more complicated schemes including up to 29 different distance measurements including eyebrow-hairline distance, lip thickness and inter-nostril separation (Young & Yamane, 1992). While this freedom in the definition of the features and spatial relationships underlying face perception provides a flexible means of describing stimuli and accommodating results obtained in a particular experiment, the fact that many of these part definitions (as well as the spatial measurements) overlap (e.g., changing an eyebrow in an eyeball-eyebrow part-based parameterization changes the “eye” part in a parameterization that does not make the eyeball-eyebrow split, and moving the eyebrow changes the eye-eyebrow configuration in the former, but the “eye” part in the latter case), has lent an element of arbitrariness to these models, and there is no consensus as to what precisely the “parts” and the “configuration” might be that the human brain according to these models presumably calculates when perceiving faces (Tsao & Freiwald, 2006). A further challenge for “feature”/”configuration” models is that no quantitative neurobiologically plausible computational model has been put forward that can take a photographic face image, calculate face “features” and their arrangement, and generate quantitative predictions for neuronal tuning and behavior. This lack of a computational implementation makes it exceedingly difficult to falsify these verbal “feature”/”configuration” models, considering that face inversion is first and foremost a quantitative deficit: While subjects are impaired at discriminating inverted faces, they are generally very well able to do so above chance.
An approach alternative to that of pre-supposing that faces are special and then trying to determine what could make faces special relative to objects from other classes is to start with the opposite assumption, i.e., that face recognition utilizes the same mechanisms (albeit not necessarily the same neurons, see below) used to recognize non-face objects, and then see whether these mechanisms are insufficient to account for the experimental data. Apart from its parsimony, this approach has two key advantages: For one, there are computational models of “generic” object recognition in cortex, e.g., (Fukushima, 1980; Perrett & Oram, 1993; Riesenhuber & Poggio, 1999b; Wallis & Rolls, 1997), based on a “simple-to-complex” hierarchical organization of visual processing, with succeeding stages being sensitive to image features of increasing complexity, and stimulus-driven learning shaping the selectivities of neurons at different stages of the processing pathway (Riesenhuber & Poggio, 2000), leading to neurons with tuning to complex, real-world objects at the highest stages in the visual processing pathway (Freedman, Riesenhuber, Poggio, & Miller, 2003; Jiang, et al., 2007; Logothetis, Pauls, & Poggio, 1995). This class of models has been validated in numerous behavioral (Serre, Oliva, & Poggio, 2007), fMRI (Jiang, et al., 2007; Jiang, et al., 2006), and electrophysiological (Cadieu, et al., 2007; Freedman, et al., 2003; Lampl, Ferster, Poggio, & Riesenhuber, 2004; Logothetis, et al., 1995; Riesenhuber & Poggio, 1999b; Serre, Kreiman, et al., 2007) studies in different species (for a recent review, see (Serre, Kreiman, et al., 2007)). Second, given its computational implementation that permits a quantitative modeling of experiments and the derivation of specific quantitative predictions for experiments, the model is falsifiable, and failures of the model can provide specific constraints as to how putative face-specific mechanisms would have to differ from generic object recognition mechanisms.
A simple shape-based and neurally plausible model of human face perception
This model-based approach to investigating the cognitive mechanisms underlying face perception is the one that we have been pursuing (Jiang, et al., 2006; Riesenhuber, Jarudi, Gilad, & Sinha, 2004). Specifically, (Jiang, et al., 2006) showed how a “simple-to-complex” generic model could not just quantitatively account for experimental data on the FIE and featural and configural effects (Riesenhuber, et al., 2004) but also for the first time make non-trivial quantitative predictions not just for behavior on a new set of faces, but also for fMRI, predictions which were then confirmed in fMRI and behavioral experiments (Jiang, et al., 2006). In our framework face perception is mediated by a population of neurons tuned to upright faces, putatively the result of extensive experience with faces. In this model, the human “fusiform face area” (FFA, (Kanwisher, McDermott, & Chun, 1997)) contains a population of sharply tuned “face neurons,” with different neurons preferring different face exemplars (for recent additional support see (Gilaie-Dotan & Malach, 2007)). This selective tuning of face neurons derives from their connectivity to lower-level afferents. Specifically, in the model (see Figure 1), model face units receive input from model units tuned to intermediate features, roughly corresponding to V4 neurons as found in the macaque (Cadieu, et al., 2007). These intermediate units are tuned to particular, weighted combinations of simpler features, e.g., complex-cell like afferents, in the same way that face units are tuned to weighted combinations of particular intermediate features. This feature combination operation integrates inputs from afferent neurons tuned to different features in different parts of the visual field (see, e.g., (Anzai, Peng, & Van Essen, 2007) for supporting data from monkey V2), thereby endowing these intermediate units not just with selectivity for particular “features” but also implicitly – due to the spatial arrangement of afferents’ receptive fields – for their “configuration”. In fact, we have recently shown that V4 neuronal selectivity can be well modeled by assuming that this selectivity arises as a result of combining spatially distributed afferents selective for simpler features (Cadieu, et al., 2007). To give two examples, one V4 neuron could receive input from two afferents, each tuned to a horizontal line, with their receptive fields at the same azimuth but different elevation, whereas another could receive input from one afferent selective for a horizontal line and another afferent selective for a vertical line with a receptive field to the lower right of that of the first afferent. The first hypothetical V4 neuron would respond well to a mouth region, whereas the latter would respond well to a left eyebrow and a nose ridge at the appropriate spatial separation. The activity of this latter neuron would thus be affected by some “configural” changes (e.g., by separating left eyebrow and nose) as well as by some “featural” changes (e.g., thickening or arching of the left eyebrow). There is thus no explicit calculation of “parts” and “configurations”. Rather, faces of different shape (be they due to explicit changes in the “configuration” or the “parts” of a face) are represented by different activation patterns over model neurons tuned to a dictionary of features of intermediate complexity, and changes in face shape lead to changes in the activation of the intermediate feature units, which in turn lead to downstream changes in the population activity of the face units as the activation of each face unit is a function of the similarity of its preferred to the current afferent activation pattern. Viewing a particular face causes a sparse activation pattern over these face neurons due to the high selectivity of face neurons (Jiang, et al., 2006) that causes only the subset of face neurons to respond whose preferred face stimuli are similar to the currently viewed face, and face discrimination is based on comparing these sparse activation patterns corresponding to different face stimuli: The discriminability of two faces is directly related to the dissimilarity of their respective face unit population activation patterns (Jiang, et al., 2006). That is, only the most strongly activated units contribute to the stimulus discrimination, as it those units which carry the most stimulus-related information (see also (Riesenhuber & Poggio, 1999a)). Indeed, recent fMRI studies have shown that behavior appears to be driven only by subsets of stimulus-related activation (Grill-Spector, Knouf, & Kanwisher, 2004; Jiang, et al., 2006; Williams, Dang, & Kanwisher, 2007), in particular those with optimal tuning for the task (see also (Jiang, et al., 2006).
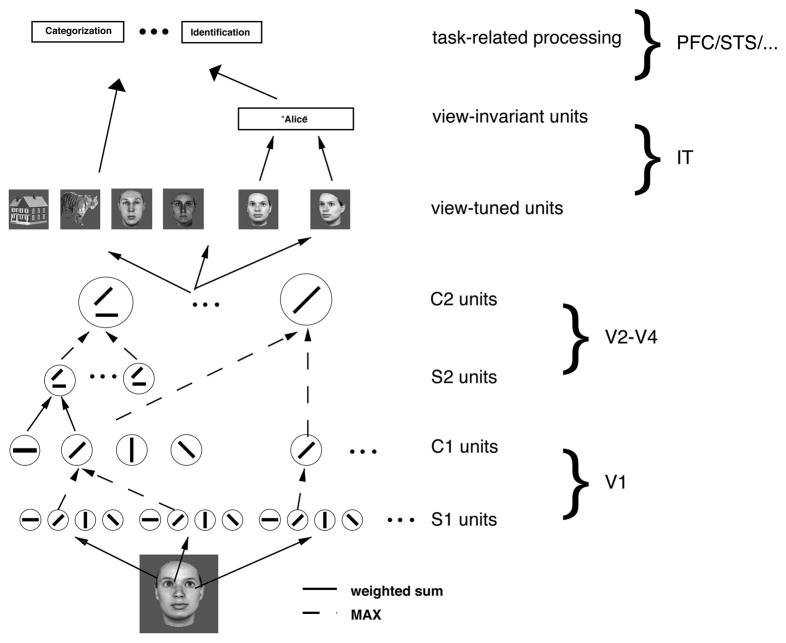
Figure 1.
Scheme of our model of face and object recognition in cortex (Jiang, et al., 2006; Riesenhuber & Poggio, 2002). It models the cortical ventral visual stream (Ungerleider & Haxby, 1994) running from primary visual cortex, V1, over extrastriate visual areas V2 and V4 to inferotemporal cortex, IT. Starting from V1 simple cells, neurons along the ventral stream show an increase in receptive field size as well as in the complexity of their preferred stimuli. At the top of the ventral stream, in anterior IT, cells are tuned to complex stimuli such as faces. The bottom part of the model (up to view-tuned units in IT) consists of a view-based module (Riesenhuber & Poggio, 1999b), which is an hierarchical extension of the classical paradigm of building complex cells from simple cells. In the model, C1 cells pool S1 inputs through a MAX-like operation (dashed green lines), where the firing rate of a pooling neuron corresponds to the firing rate of the strongest input, which improves invariance to local changes in position and scale while preserving stimulus selectivity (Riesenhuber & Poggio, 1999b). At the next layer (S2), cells pool the activities of earlier neurons with different tuning, yielding selectivity to more complex patterns as found experimentally, e.g., in V4 (Cadieu, et al., 2007). The underlying operation is in this case more “traditional”: a weighted sum followed by a sigmoidal (or Gaussian) transformation (solid lines). These two operations work together to progressively increase feature complexity and position (and scale) tolerance of units along the hierarchy, in agreement with physiological data. The output of the view-based module is represented by view-tuned model units (VTUs) that exhibit tight tuning to rotation in depth but are tolerant to scaling and translation of their preferred object view, with tuning properties quantitatively similar to those found in IT (Logothetis, et al., 1995; Riesenhuber & Poggio, 1999b). These units can then provide input to task-specific circuits located in higher areas, e.g., prefrontal cortex (PFC).
Neural mechanisms for “gholistic” processing
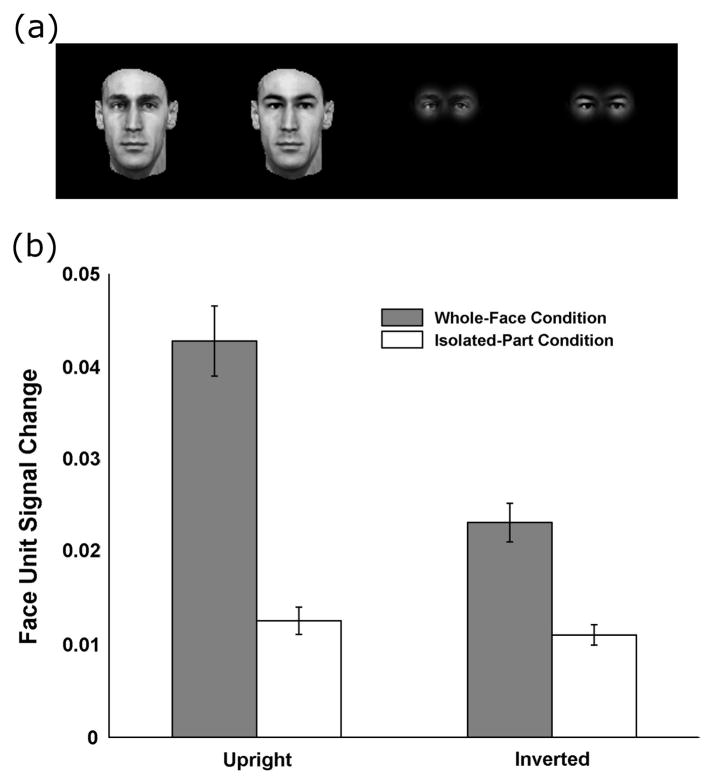
Of key relevance for the present discussion, the model thus provides a simple candidate mechanism for “holistic” processing in the form of a neural representation tuned to upright faces: While these model neurons respond well and selectively to particular upright faces, they respond less to and differentiate poorly between inverted faces and thus do not provide as good a basis to discriminate inverted faces, accounting for the behavioral FIE, as shown in (Jiang, et al., 2006). Thus, this model in which upright face perception is mediated by neurons tuned to whole faces is far from “a toning down of the integrative views of face perception” ((Rossion, 2008), p. 284): Rather, as we stated in 2004 (Riesenhuber, et al., 2004), a representation composed of neurons tuned to upright faces provides a neural substrate for such a “holistic representation” argued for by the behavioral experiments. Specifically, Figure 2 illustrates how these model units tuned to upright faces show holistic tuning by replicating the classic experiment by Tanaka and Farah (Tanaka & Farah, 1993), which found that subjects were much better at recognizing a particular face part (e.g., an eye region) in a complete face than when the same part was presented in isolation: Similarly, the left two bars in Figure 2(b) show that model face units show a much greater signal change in face unit activation for two whole face images that only differ in the eye region vs. presenting the two different eye regions separately (i.e., without a whole face context). Thus, our 2004 paper and the 2006 model anticipate Rossion’s statement in his recent paper that “faces are processed holistically because of their holistic representation in the visual system” ((Rossion & Boremanse, 2008), p. 10), and even more so with the idea of “a framework according to which holistic perception of faces is highly dependent on visual experience” (ibid., p.10), as the tightly tuned face representation in the FFA (whose tight tuning has been suggested to be a result of extensive experience with faces (Jiang, et al., 2006)) provides just such a framework. This experience-based model not only fits with recent developmental data (Golarai, et al., 2007), but also offers straightforward explanations for other face-specific phenomena such as the other-race effect (see discussion in (Jiang, et al., 2006)), that would be difficult to account for with a model in which experience served to, e.g., develop a general-purpose “configural module” for “expertise processing” or the like (given that faces in general do not differ appreciably in their facial “configurations” across race groups).
Figure 2.
Face units in the model show holistic tuning to upright faces. (a) Example stimuli, from left to right: two faces with different eye regions but otherwise identical (whole-face condition), and then the same two faces with only the eye regions showing (isolated-part condition). (b) The average face-unit signal change induced by a different eye region (across all combinations of 20 faces and 19 sets of eyes for a total of 380 images, each run both upright and inverted). Face-unit signal change is defined as the euclidean distance between the activation patterns of the most active face units to the two stimuli in a pair (see (Jiang, et al., 2006)). The magnitude of this distance is analogous to how “different” two faces look, and is the measure used to predict behavioral face discrimination. Note that there is strong holistic tuning for upright faces (large difference between the two left bars), but less so for inverted faces (two right bars). Moreover, the model predicts an inversion effect for whole faces (gray bars), but not for isolated face parts (white bars), in agreement with behavioral data (Tanaka & Farah, 1993).
Note that the model (see white bars in Figure 2) predicts no inversion effect for eye regions presented as isolated parts but a strong inversion effect for the same eye regions embedded in a whole face context (gray bars), compatible with the experimental data (Tanaka & Farah, 1993). Moreover, inversion strongly reduces holistic processing (compare the VTU activation distance in the “whole face” condition for upright vs. inverted faces in Figure 2), as face units tuned to upright faces respond only at low levels to inverted faces, their response to inverted faces being driven by afferent features less affected by image plane rotation (e.g., the putative “mouth” feature described above).
Interestingly, given the absence of a special status of face “parts” and “configuration” in the model, which instead both are rather examples of shape changes that would cause distributed and overlapping changes in the activation patterns at the intermediate feature level, the “simple-to-complex” account predicts that comparable FIE’s can be associated with “featural” as well as with “configural” changes, as the shape-based neuronal face representation is well suited for upright, but not inverted faces, irrespective of whether face pairs differ by features or configuration.
This was the main prediction of the 2004 paper (Riesenhuber, et al., 2004). At the time, this was a somewhat unfashionable prediction. Back then, the thinking was that there was little, if any, inversion effect for “featural” changes, the FIE being due to “configural processing” not being available for inverted faces. This widespread view was expressed, e.g., in a 2002 review paper (Rossion & Gauthier, 2002): “First, the FIE for full faces seems to be entirely accounted for by the distinctive relational information present locally” (p.64).
But, in youthful exuberance we likewise wrote in (Riesenhuber, et al., 2004): “If two modifications to the shape of a face – be they a result of changes in the ‘configuration’ or in the ‘features’ – influence discrimination performance to an equal degree for upright faces, they should also have an equal effect on the discrimination of inverted faces.” While this is likely true on average if changes are distributed over many features (as our data and those of others (Yovel & Kanwisher, 2004) have shown), it is possible to come up with scenarios in which the FIE can differ even for equalized performance in the upright orientation, depending on the tolerance of afferent feature detectors to rotations in the image plane: Neurons tuned to some intermediate features might also respond well to inverted faces (e.g., the hypothetical two-horizontal lines feature from above), whereas others would not (e.g., the horizontal-to-upper-left-of-vertical), and depending on which of these intermediate units provide input to particular face units, their responses can be more or less affected by specific transformations, be they changes in “features”, “configuration”, or image-plane orientation. Again, the FIE is not determined by how much a shape change affects a face’s “configuration”, but rather by how it changes the activity distribution over the neurons tuned to intermediate features providing input to the face neurons. Very interestingly, in their recent paper (Goffaux & Rossion, 2007), Rossion and Goffaux provide strong support for this model prediction, showing that replacing the eye region of a face (a bona fide “featural” change) causes an FIE that is as strong as (if not slightly stronger than) that caused by a horizontal displacement of the eyes (a bona fide “configural” change), see Fig. 3 in (Rossion, 2008). As our (Riesenhuber, et al., 2004), Yovel and Kanwisher’s (Yovel & Kanwisher, 2004) and now also Goffaux and Rossion’s data (Goffaux & Rossion, 2007) show, featural changes can be associated with substantial FIE’s of comparable magnitude as those caused by “configural” changes, strongly arguing against “distinctive relational information” as the only contributor to an FIE, and arguing against a special status of “configural” information in underlying the FIE. This has resulted in a welcome convergence of views. Nevertheless, despite this increasing agreement in spirit, (Rossion, 2008) contained some specific criticisms about our 2004 paper. We will next address these criticisms in detail, and then show how the model of (Jiang, et al., 2006) can provide a framework to discuss the recent results of (Rossion & Boremanse, 2008).
Comments on specific issues raised by Rossion (2008)
Performance across conditions: The issue of equalization
Rossion writes, “Riesenhuber et al. (2004) did not [Rossion’s emphasis] equalize performance for configural and featural trials upright.” This is a somewhat surprising statement, considering that (Riesenhuber, et al., 2004) explicitly stated that “faces were selected so that performance in upright featural and configural trials was comparable”, referring to a pilot experiment in the appendix to that paper. Faces used in the main experiment in (Riesenhuber, et al., 2004) were selected based on these pilot experiments, choosing face pairs (either “same” pairs or those with “featural” or “configural” differences) on which average subject performance in the pilot experiment was about 80% correct. Not surprisingly, the subject group of the main experiment in (Riesenhuber, et al., 2004), being composed of all new subjects, showed slightly different performance on the same images, averaging 85% correct on the featural vs. 77% on the configural trials, a difference that was not statistically significant, p>0.1 (note that blocking the same images by change type, as in Experiment 3 in (Riesenhuber, et al.), induced performance differences in the upright condition, as predicted, see discussion below). Unlike Rossion, we very much agree with Yovel and Kanwisher (Yovel & Kanwisher, 2004) that it is important to equalize performance on the different trial types (in particular, those with “featural” vs. “configural” changes) in the upright orientation, especially when reporting findings of a null effect of stimulus orientation on discrimination performance for particular stimulus transformations: If performance were at ceiling for feature-change stimuli in the upright orientation, then a relatively small inversion effect for these face stimuli might be trivial because the stimuli might be so different that they are easy to discriminate also in the inverted orientation. For instance, the high performance on featural change trials in (Freire, Lee, & Symons, 2000) of 91% (vs. 81% for configural change trials) in the upright orientation might have been due to ceiling effects for some featural change face pairs, potentially accounting for the decreased FIE for “featural” vs. “configural” changes. The easiest way to avoid such problems is to equalize performance at non-ceiling rates, e.g., 80% (that are still high enough to conversely avoid floor effects in the inverted orientation). In addition, it needs to be noted that there are other experimental artifacts that might bias inversion effects for different change types (see the discussion on blocking effects below), and just controlling one issue (e.g., ensuring non-ceiling performance in the upright orientation) of course does not simultaneously eliminate all other potential confounds (e.g., blocking artifacts).
Reaction times
Rossion then raises the issue of reaction times (RT), wondering, while no differences in performance were found for the different changes types, whether there might at least be differences in RT for the different change types in the experiment of (Riesenhuber, et al., 2004). This is not the case: Performing a repeated-measures ANOVA with factors of orientation and change type (“featural”, “configural”, and “same”) on the correct response times (after removing outliers further than two standard deviations from the mean) reveals a significant effect of orientation (p=0.03, with longer average response times for inverted trials, 739 ms vs. 653 ms for upright trials), but no significant effect of change type (p>0.5), and no interaction (p>0.1). The reaction time data therefore are consistent with the performance data and the assumption that featural and configural trials in (Riesenhuber, et al., 2004) were of equal difficulty.
“Featural” vs. “configural” image changes
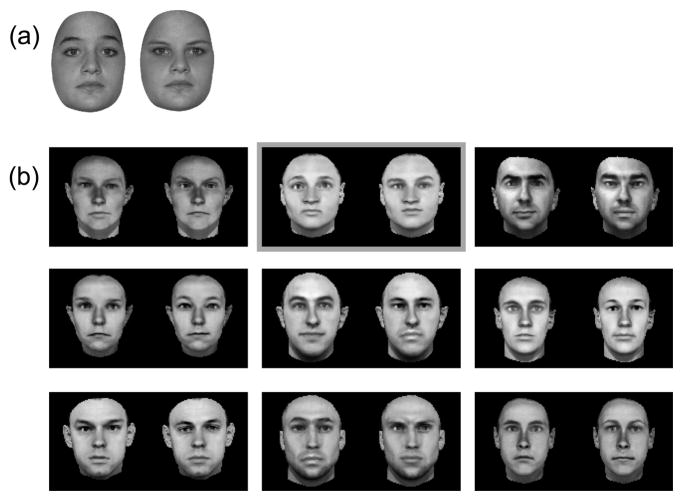
Rossion further criticized how stimuli in (Riesenhuber, et al., 2004) were generated, in particular that “feature” change stimuli were created by replacing the whole eye region (including eyebrows) between faces, replacing one individual’s eyes with those from another subject, at the same location (as in other studies, e.g., (Rotshtein, Geng, Driver, & Dolan, 2007)). Specifically, Rossion claims that “the faces in these ‘featural’ trials could be distinguished based on metric distances between features: eye-eyebrow distance could be used as a cue alone”. Rossion illustrates this claim with a pair of faces he provides, implying that this is representative of our stimuli, referring to a pair of faces shown in (Riesenhuber, et al., 2004). In Figure 3, we provide both face pairs for comparison (the one shown in (Riesenhuber, et al., 2004) is the middle one in the top row of panel b), along with a few (randomly selected) others. It is obvious that while the face pair given by Rossion in (Rossion, 2008) can serve as an illustration of how much eye-eyebrow distance can vary in human faces, it is not representative of the stimuli used in (Riesenhuber, et al., 2004). As apparent from Figure 3, it is in fact the intended “featural” change that is most evident in the “featural” change pairs in (Riesenhuber, et al., 2004), rather than “eye-eyebrow distance changes”.
Figure 3.
Examples of “featural change” image pairs. (a) is from (Rossion, 2008). (b) Examples of images used in our studies (Riesenhuber, et al., 2004). The center image in the top row (framed in gray) is the one shown in Figure 1 of (Riesenhuber, et al., 2004).
A more fundamental problem with the argument that feature changes also affect some “configural” measure goes back to the initial discussion of the arbitrariness of “configural” models: unless featural changes are purely limited to color or brightness changes (which do not show an FIE (Leder & Carbon)), it appears that one can always come up with a putative configural metric that is affected by a particular featural change. For instance, in the case of a featural change involving the eye region, one can choose to center the replacement eyes at the same location as the original eyes. If the eyes are not of exactly the same outline as the ones being replaced, this will cause changes of metrics such as “top of eye to bottom of eyebrow” distance, “nasal edge of eye to nose” distance, eye-chin distance, eye-ear distance etc. etc., making it possible to ascribe observed FIEs in that case to these “configural” changes, while at the same time demonstrating the limited usefulness of “feature” vs. “configuration” dichotomies.
Task-specific modulation of the FIE: The effect of blocking
A key part of our 2004 paper (Riesenhuber, et al., 2004) was the demonstration that the FIE could be modulated by task strategies, and in particular that the failure of some prior experiments to find an inversion effect for featural changes could have been due to the subjects’ using artifactual strategies (e.g., non-holistic ones, not based on activations over the face units tuned to upright faces). As we wrote in the 2004 paper: “For instance, in a blocked design, it is conceivable for subjects in featural trials to use a strategy that does not rely on the visual system’s face representation but rather focuses just on detecting local changes in the image, for example, in the eye region. This would then lead to a performance less affected by inversion. However, such a local strategy would not be optimal for configural trials since, in these trials, the eye itself does not change, only its position with respect to the rest of the face. Thus, configural trials can profit from a ‘holistic’ strategy (i.e. looking at the whole face, which for upright but not for inverted faces presumably engages the learned (upright) face representation), which would in turn predict a strong effect of inversion.” Indeed, in the paper (Riesenhuber, et al., 2004) we showed that just blocking trials according to change type, i.e., presenting all “featural change” trials together (including “same” and “different” trials, whether upright or inverted), either preceded or followed (depending on subject group) by all “configural” trials could induce strong modulations of behavioral performance, as predicted: In subjects first exposed to “configural” trials followed by the featural trials, subjects showed no difference in performance over all “configural” vs. all “featural” trials (p=0.19), as in the unblocked experiment where “featural” and “configural” trials were randomly interleaved. However, in the “featural first” group, performance was highly significantly different between “featural” and “configural” trials (p=0.001), due to poor performance on the “configural” trials, compatible with the prediction that presenting “featural” trials first would bias subjects towards using a part-based, local strategy that then failed on the “configural” trials, whereas subjects in the “configural first” group would use the default, holistic strategy to discriminate faces. This is supported by an ANOVA that found a significant interaction between change type (“featural” vs. “configural”) and blocking type (“featural first” vs. “configural first”, p<0.02), supporting that blocking can affect subjects’ strategies for face discrimination, as predicted. This adds to previous reports that the degree of FIE on a fixed set of images can be manipulated by task variations (e.g., (Farah, Tanaka, & Drain, 1995)). Regarding the triple interaction between blocking type, change type, and orientation discussed by Rossion, we would not predict this interaction to necessarily be significant (and indeed, it is non-significant in our data), since the effect of blocking and the putative associated shifts in face processing strategy are not necessarily specific for orientation: On configural trials, if subjects adopt a featural/local strategy where they focus on local features (which are not affected by configural changes) then their performance decreases regardless of orientation. On featural trials, if subjects adopt the featural/local strategy, then for inverted trials we expect a performance increase (as observed, see Riesenhuber et al., 2004, while for upright trials we expect any change in performance to depend on whether the local strategy can identify local changes in upright faces better than the holistic face representation. In our data, we observed a slight performance increase for upright featural change trials for subjects in the “featural first” vs. the “configural first” groups. The triple interaction is therefore not a robust prediction, whereas the interaction of change type and blocking type is: Subject performance on featural and configural trials should vary depending on whether they use a “featural” (i.e., local) or “configural” strategy, and indeed it does.
As noted above, we should point out again that these factors are not the only reasons why experiments can fail to find an FIE for featural changes, ceiling effects being another reason, for instance. Furthermore, in response to Rossion’s statement that failure to find an effect of blocking in one experiment (Yovel & Kanwisher, 2004) “indicate[s] that randomizing or blocking configural and featural trials did not matter”, it is worth recalling that absence of evidence is not evidence of absence: If subjects fail to realize that the stimuli permit the effective use of a part-based strategy, but rather process all face stimuli holistically independent of change type, then, trivially, one would not expect an effect of blocking.
In (Rossion, 2008), Rossion then presents data from (Goffaux & Rossion, 2007) claiming that those data show that blocking does not affect the inversion effect for features vs. configuration. Again, the failure to find an effect of blocking could just be due to the fact that Rossion’s subjects did not pick up on the difference, failing to realize that focusing attention on the eye region would be sufficient for discrimination in the “feature-change only” blocks. However, prompted by the somewhat curious finding that subjects in (Goffaux & Rossion, 2007) appeared to perform better when trials were randomized than when trials were blocked (see Figure 3 in (Rossion, 2008)), we consulted the original paper (Goffaux & Rossion, 2007). While there is no discussion in the paper of the apparent performance improvement on randomized trials, reading the paper revealed that, surprisingly, blocking in (Goffaux & Rossion, 2007) was done by orientation and not by change type! This merits repeating: The point in our paper (Riesenhuber, et al., 2004) criticized by Rossion (Rossion, 2008) was that blocking featural vs. configural trials, i.e., by change type, can induce subjects to adopt change type-specific, in particular local vs. holistic strategies, as discussed above. What Goffaux and Rossion present in their paper are data for a blocking by orientation, i.e., upright vs. inverted trials! This is a very different manipulation that would not be expected to induce qualitative changes in task strategies for featural vs. configural change image pairs (our hypothesis in (Riesenhuber, et al., 2004) indeed was that if subjects cannot predict the change type, they would default to normal holistic face processing, leading to inversion effects for both “featural” and “configural” changes, as found in the main experiment and as outlined above). The fact that Goffaux and Rossion in (Goffaux & Rossion, 2007) did not find an effect of blocking on the FIE for featural vs. configural changes is not only not surprising, it is also irrelevant as they investigated the wrong blocking scheme. Thus, the statement in (Rossion, 2008) that “there is no evidence whatsoever that this blocking factor plays any role in the absence of significantly larger inversion costs for configural than featural trials reported by Riesenhuber and colleagues (2004)”, p.5) is based on comparing apples and oranges.
In any case, it seems that Rossion does not dispute that external factors such as subjects’ expectations can influence the FIE (cf. p. 285, “if two individual faces differ by local elements (i.e., the shape of the mouth), the effect of face inversion on the performance will be substantial. This will be especially true when there is an uncertainty about the identity and localization of the diagnostic feature on the face,” emphasis added). This was the main point of the manipulation in our paper: Blocking the stimuli, even without any change in instructions, can change whether a difference in performance between featural and configural changes is found or not, likely by affecting subjects’ cognitive strategies. Given further Rossion’s aforementioned own data that show a substantial inversion effect for featural changes equaling that of some configural changes, there is now a nice convergence of views and support for a theory in which holistic processing arises from the use of a neural population of neurons tuned to upright faces which only responds poorly to inverted faces, producing an inversion effect.
Composite Face Effect
Our shape-based computational model appears to also hold promise to account for some aspects of the Composite Face (CF) effect (Wolff and Riesenhuber, unpublished observations): Face units in the model respond poorly to misaligned faces, similar to their poor responses for inverted faces and the observed reduction of holistic processing, cf. Figure 2. Indeed, it is an interesting question whether inversion completely abolishes holistic processing or not. Some studies have found evidence for holistic processing for inverted faces (e.g., (Murray, 2004)) while others failed to do so (e.g., (Tanaka & Farah, 1993) – note, however, that in the latter study subjects were asked to identify particular face parts (“Is this Larry nose?”), which could have led subjects to only pay attention to the relevant parts of the face in the inverted orientation even in the “whole-face” condition, as the holistic representation would not be expected to be effective for inverted faces). Likewise, in Rossion’s own CF data (Rossion & Boremanse, 2008), it appears that there is still some holistic processing even for the inverted orientation2: As Fig. 3 in (Rossion & Boremanse, 2008) shows, subject performance still shows a sizable effect of alignment in the inverted orientation: In the crucial “same” condition, performance on aligned face images is around 77% vs. around 92% for misaligned images, a difference that is only a bit smaller than the difference in the upright orientation (around 67% vs. 89%, respectively). This indicates that even in the inverted orientation, the aligned faces were still processed somewhat holistically, compatible with the case of inverted faces shown in Figure 2, leading to the poorer performance on aligned faces relative to misaligned faces.
In summary, we agree with Dr. Rossion that upright faces are processed in a holistic fashion, and we are glad that we could use this opportunity to clarify a few points and show that there is already a biologically plausible model that provides a concrete computational implementation of holistic face processing.
Acknowledgments
This research was supported in part by an NSF CAREER Award (#0449743), and NIMH grants R01MH076281 and P20MH66239.
Footnotes
Note that in this paper, we refer to named parts of the face, such as eyes, mouth, and nose, eyebrows etc. as face “parts”, to contrast them to visual “features”, a term we use to refer to the preferred stimuli of neurons below the holistic face neuron level (see Figure 1 and below), which may or may not correspond to face “parts”. If we need to refer to “face features” in their traditional sense in the face perception literature, i.e., as eyes, mouth, nose etc., then we will use the term in quotes.
On a side note, it appears that Figure 4 in (Rossion, 2008) which describes the CF results from (Rossion & Boremanse, 2008) is incorrect, as it shows higher accuracy and faster reaction times in the aligned case vs. the misaligned case, just the opposite of the classical CF effect.
References
- Anzai A, Peng X, Van Essen DC. Neurons in monkey visual area V2 encode combinations of orientations. Nat Neurosci. 2007;10(10):1313–1321. doi: 10.1038/nn1975. [DOI] [PubMed] [Google Scholar]
- Cadieu C, Kouh M, Pasupathy A, Connor CE, Riesenhuber M, Poggio T. A model of V4 shape selectivity and invariance. J Neurophysiol. 2007;98(3):1733–1750. doi: 10.1152/jn.01265.2006. [DOI] [PubMed] [Google Scholar]
- Carey S, Diamond R. Why faces are and are not special: An effect of expertise. J Exp Psychol Gen. 1986;115:107–117. doi: 10.1037//0096-3445.115.2.107. [DOI] [PubMed] [Google Scholar]
- Farah MJ, Tanaka JW, Drain HM. What causes the face inversion effect? J Exp Psychol Hum Percept Perform. 1995;21(3):628–634. doi: 10.1037//0096-1523.21.3.628. [DOI] [PubMed] [Google Scholar]
- Freedman DJ, Riesenhuber M, Poggio T, Miller EK. Comparison of Primate Prefrontal and Inferior Temporal Cortices during Visual Categorization. J Neurosci. 2003;23:5235–5246. doi: 10.1523/JNEUROSCI.23-12-05235.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freire A, Lee K, Symons LA. The face-inversion effect as a deficit in the encoding of configural information: direct evidence. Perception. 2000;29(2):159–170. doi: 10.1068/p3012. [DOI] [PubMed] [Google Scholar]
- Fukushima K. Neocognitron: a self organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol Cybern. 1980;36(4):193–202. doi: 10.1007/BF00344251. [DOI] [PubMed] [Google Scholar]
- Gilaie-Dotan S, Malach R. Sub-exemplar shape tuning in human face-related areas. Cereb Cortex. 2007;17(2):325–338. doi: 10.1093/cercor/bhj150. [DOI] [PubMed] [Google Scholar]
- Goffaux V, Rossion B. Face inversion disproportionately impairs the perception of vertical but not horizontal relations between features. J Exp Psychol Hum Percept Perform. 2007;33(4):995–1002. doi: 10.1037/0096-1523.33.4.995. [DOI] [PubMed] [Google Scholar]
- Golarai G, Ghahremani DG, Whitfield-Gabrieli S, Reiss A, Eberhardt JL, Gabrieli JD, et al. Differential development of high-level visual cortex correlates with category-specific recognition memory. Nat Neurosci. 2007;10(4):512–522. doi: 10.1038/nn1865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grill-Spector K, Knouf N, Kanwisher N. The fusiform face area subserves face perception, not generic within-category identification. Nat Neurosci. 2004;7(5):555–562. doi: 10.1038/nn1224. [DOI] [PubMed] [Google Scholar]
- Haig ND. The effect of feature displacement on face recognition. Perception. 1984;13(5):505–512. doi: 10.1068/p130505. [DOI] [PubMed] [Google Scholar]
- Jiang X, Bradley E, Rini RA, Zeffiro T, Vanmeter J, Riesenhuber M. Categorization training results in shape- and category-selective human neural plasticity. Neuron. 2007;53(6):891–903. doi: 10.1016/j.neuron.2007.02.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang X, Rosen E, Zeffiro T, Vanmeter J, Blanz V, Riesenhuber M. Evaluation of a shape-based model of human face discrimination using FMRI and behavioral techniques. Neuron. 2006;50(1):159–172. doi: 10.1016/j.neuron.2006.03.012. [DOI] [PubMed] [Google Scholar]
- Kanwisher N, McDermott J, Chun MM. The fusiform face area: a module in human extrastriate cortex specialized for face perception. J Neurosci. 1997;17(11):4302–4311. doi: 10.1523/JNEUROSCI.17-11-04302.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lampl I, Ferster D, Poggio T, Riesenhuber M. Intracellular Measurements of Spatial Integration and the MAX Operation in Complex Cells of the Cat Primary Visual Cortex. J Neurophys. 2004;92:2704–2713. doi: 10.1152/jn.00060.2004. [DOI] [PubMed] [Google Scholar]
- Leder H, Carbon CC. Face-specific configural processing of relational information. Br J Psychol. 2006;97(Pt 1):19–29. doi: 10.1348/000712605X54794. [DOI] [PubMed] [Google Scholar]
- Logothetis NK, Pauls J, Poggio T. Shape representation in the inferior temporal cortex of monkeys. Curr Biol. 1995;5:552–563. doi: 10.1016/s0960-9822(95)00108-4. [DOI] [PubMed] [Google Scholar]
- Murray JE. The ups and downs of face perception: evidence for holistic encoding of upright and inverted faces. Perception. 2004;33(4):387–398. doi: 10.1068/p5188. [DOI] [PubMed] [Google Scholar]
- Perrett D, Oram M. Neurophysiology of shape processing. Image Vision Comput. 1993;11:317–333. [Google Scholar]
- Riesenhuber M, Jarudi I, Gilad S, Sinha P. Face processing in humans is compatible with a simple shape-based model of vision. Proc R Soc Lond B (Suppl) 2004;271:S448–450. doi: 10.1098/rsbl.2004.0216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riesenhuber M, Poggio T. Are cortical models really bound by the “binding problem”? Neuron. 1999a;24(1):87–93. 111–125. doi: 10.1016/s0896-6273(00)80824-7. [DOI] [PubMed] [Google Scholar]
- Riesenhuber M, Poggio T. Hierarchical models of object recognition in cortex. Nat Neurosci. 1999b;2:1019–1025. doi: 10.1038/14819. [DOI] [PubMed] [Google Scholar]
- Riesenhuber M, Poggio T. Models of object recognition. Nat Neurosci Supp. 2000;3:1199–1204. doi: 10.1038/81479. [DOI] [PubMed] [Google Scholar]
- Riesenhuber M, Poggio T. Neural Mechanisms of Object Recognition. Curr Opin Neurobiol. 2002;12:162–168. doi: 10.1016/s0959-4388(02)00304-5. [DOI] [PubMed] [Google Scholar]
- Rossion B. Picture-plane inversion leads to qualitative changes of face perception. Acta Psychol (Amst) 2008;128(2):274–289. doi: 10.1016/j.actpsy.2008.02.003. [DOI] [PubMed] [Google Scholar]
- Rossion B, Boremanse A. Nonlinear relationship between holistic processing of individual faces and picture-plane rotation: evidence from the face composite illusion. J Vis. 2008;8(4):3, 1–13. doi: 10.1167/8.4.3. [DOI] [PubMed] [Google Scholar]
- Rossion B, Gauthier I. How does the brain process upright and inverted faces? Behav Cogn Neurosci Rev. 2002;1(1):63–75. doi: 10.1177/1534582302001001004. [DOI] [PubMed] [Google Scholar]
- Rotshtein P, Geng JJ, Driver J, Dolan RJ. Role of features and second-order spatial relations in face discrimination, face recognition, and individual face skills: behavioral and functional magnetic resonance imaging data. J Cogn Neurosci. 2007;19(9):1435–1452. doi: 10.1162/jocn.2007.19.9.1435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serre T, Kreiman G, Kouh M, Cadieu C, Knoblich U, Poggio T. A quantitative theory of immediate visual recognition. Prog Brain Res. 2007;165:33–56. doi: 10.1016/S0079-6123(06)65004-8. [DOI] [PubMed] [Google Scholar]
- Serre T, Oliva A, Poggio T. A feedforward architecture accounts for rapid categorization. Proc Natl Acad Sci U S A. 2007;104(15):6424–6429. doi: 10.1073/pnas.0700622104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka JW, Farah MJ. Parts and wholes in face recognition. Q J Exp Psychol A. 1993;46(2):225–245. doi: 10.1080/14640749308401045. [DOI] [PubMed] [Google Scholar]
- Tsao DY, Freiwald WA. What’s so special about the average face? Trends Cogn Sci. 2006;10(9):391–393. doi: 10.1016/j.tics.2006.07.009. [DOI] [PubMed] [Google Scholar]
- Ungerleider LG, Haxby JV. ‘What’ and ‘where’ in the human brain. Curr Opin Neurobiol. 1994;4(2):157–165. doi: 10.1016/0959-4388(94)90066-3. [DOI] [PubMed] [Google Scholar]
- Wallis G, Rolls ET. A model of invariant recognition in the visual system. Prog Neurobiol. 1997;51:167–194. doi: 10.1016/s0301-0082(96)00054-8. [DOI] [PubMed] [Google Scholar]
- Williams MA, Dang S, Kanwisher NG. Only some spatial patterns of fMRI response are read out in task performance. Nat Neurosci. 2007;10(6):685–686. doi: 10.1038/nn1900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin RK. Looking at upside-down faces. J Exp Psychol. 1969;81:141–145. [Google Scholar]
- Young MP, Yamane S. Sparse population coding of faces in the inferotemporal cortex. Science. 1992;256(5061):1327–1331. doi: 10.1126/science.1598577. [DOI] [PubMed] [Google Scholar]
- Yovel G, Kanwisher N. Face perception: domain specific, not process specific. Neuron. 2004;44(5):889–898. doi: 10.1016/j.neuron.2004.11.018. [DOI] [PubMed] [Google Scholar]