Abstract
Response times on test items are easily collected in modern computerized testing. When collecting both (binary) responses and (continuous) response times on test items, it is possible to measure the accuracy and speed of test takers. To study the relationships between these two constructs, the model is extended with a multivariate multilevel regression structure which allows the incorporation of covariates to explain the variance in speed and accuracy between individuals and groups of test takers. A Bayesian approach with Markov chain Monte Carlo (MCMC) computation enables straightforward estimation of all model parameters. Model-specific implementations of a Bayes factor (BF) and deviance information criterium (DIC) for model selection are proposed which are easily calculated as byproducts of the MCMC computation. Both results from simulation studies and real-data examples are given to illustrate several novel analyses possible with this modeling framework.
Keywords: speed, accuracy, IRT, response times
1. Introduction
Response times (RTs) on test items can be a valuable source of information on test takers and test items, for example, when analyzing the speededness of the test, calibrating test items, detecting cheating, and designing a test (e.g., Bridgeman & Cline, 2004; Wise & Kong, 2005; van der Linden & Guo, 2008; van der Linden, Breithaupt, Chuah, & Zang, 2007; van der Linden, 2007). With the introduction of computerized testing, their collection has become straightforward.
It is important to make a distinction between the RTs on the test items and the speed at which a test taker operates throughout the test, especially when each person takes a different selection of items, as in adaptive testing. For two different test takers, it is possible to operate at the same speed, but produce entirely different RTs because the problems formulated in their items require different amounts of information to be processed, different problem-solving strategies, etc. Models for RTs should therefore have separate parameters for the test takers’ speed and the time intensities of the items.
Another potential confounding relationship is that between speed and accuracy. It is well known that on complex tasks, these two are different constructs (see, for instance, Kennedy, 1930; Schnipke & Scrams, 2002). Tate (1948) was one of the first to examine the relationship between speed and accuracy on different tests. He concluded that for a controlled level of accuracy, each test taker worked at a constant speed. Furthermore, test takers working at a certain speed do not necessarily demonstrate the same accuracy.
Some of these findings can be explained by the well-known speed-accuracy trade-off (e.g., Luce, 1986). The trade-off reflects the fact that speed and accuracy are main determinants of each other. Also, they are negatively related. When a person chooses to increase his speed, then his accuracy decreases. But once his speed is fixed, his accuracy remains constant. Observe that this trade-off involves a within-person constraint only; it does not enable us to predict the speed or accuracy of one person from another taking the same test. In order to model the relationship between speed and accuracy adequately, we therefore need a model with different levels. This multilevel perspective has not yet been dominant in the psychometric literature on RT modeling. Instead, attempts have been made to integrate speed parameters or RTs into traditional single-level response models (Verhelst, Verstralen, & Jansen, 1997) or, reversely, response parameters into RT models (Thissen, 1983). However, a hierarchical framework for modeling responses and RTs was introduced in van der Linden (2008). The framework has separate first-level models for the responses and RTs. For the response model, a traditional item-response theory (IRT) model was chosen. For the RTs, a lognormal model with separate person and item parameters was adopted, which has nice statistical properties and fitted actual response time data very well (van der Linden, 2006). At the second level, the joint distributions of the person and item parameters in the two first-level models were modeled separately.
Observe that because the framework in this paper does not model a speed-accuracy tradeoff, it can be used just as well to analyze responses and RTs to instruments for noncognitive domains, such as attitudes scales or personality questionnaires.
Because the first-level parameters capture all systematic variation in the RTs, they can be assumed to be conditionally independent given the speed parameter. Likewise, the responses and RTs are assumed to be conditionally independent given the ability and speed parameter. Such assumptions of conditional independence are quite common in hierarchical modeling but may seem counterintuitive in the current context, where the speed-accuracy trade-off is often taken to suggest that the frequency of the correct responses increases if the RTs go up. However, this confusion arises when the earlier distinction between speed and RT is overlooked. The trade-off controls the choice of the levels of speed and accuracy by the individual test taker whereas the conditional independence assumptions address what happens with his response and RT distributions after the levels of speed and accuracy have been fixed.
Besides being a nice implementation of the assumptions of local independence for RTs and responses, this framework allows for the incorporation of explanatory variables to identify factors that explain variation in speed and accuracy between individuals who may be nested within groups. The current paper addresses this possibility; its goal is to extend the framework with a third level with regression and group effects and to make this result statistically tractable. The result is a multivariate multilevel model for mixed response variables (binary responses and continuous RTs). At the person level, just as in the original framework, it allows us to measure both accuracy and speed. Test takers can therefore be compared to each other with respect to these measures. But at the higher levels, the extended framework also allows us to identify covariates and group memberships that explain the measures as well as their relationships. Also, the item parameters are allowed to correlate.
Analysis of the extended model is performed in a fully Bayesian way. The motivation for the Bayesian treatment is its capability of handling complex models with many parameters that take all possible sources of variation into account. A new Gibbs sampling procedure (Geman & Geman, 1984; Gelfand & Smith, 1990) was developed which applies not only to the current framework but to the entire class of nonlinear multivariate multilevel models for mixed responses with balanced and unbalanced designs. All parameters can be estimated simultaneously without the need to fine-tune any parameters to guarantee convergence, for instance, as in a Metropolis- Hastings (MH) algorithm. Proper prior distributions can be specified that can be used both to incorporate a set of identifying restrictions for the model and to reflect the researcher’s ideas about the parameter values and uncertainties. The estimation method can also handle incomplete designs with data missing at random.
A model-specific implementation of the Bayes factor (Kass & Raftery, 1995) and the deviance information criterion (DIC) (Spiegelhalter, Best, Carlin, & van der Linde, 2002) is given, which can be used (i) to test specific assumptions about the distribution of speed and accuracy in a population of test takers and (ii) to iteratively build a structural multivariate multilevel component for the latent person parameters with fixed and random effects. Both statistics can be computed as by-products of the proposed Gibbs sampler. The DIC requires an analytic expression of the deviance associated with the likelihood of interest. Such an expression is offered for the multivariate multilevel model given the complete data, which includes augmented continuous data given the binary responses (Albert, 1992), integrating out both random person parameters and other random regression effects at the level of groups of respondents. The posterior expectation of this complete DIC is taken over the augmented data using the output from the MCMC algorithm. Properties of the DIC, as well as the Bayes factor, were analyzed in a study with simulated data.
In the next sections, we describe the entire model, specify the prior distributions, discuss the Gibbs sampler, and show how to apply the Bayes factor and the DIC to the current model. Then in a simulation study, the performance of the Gibbs sampler is addressed, whereby our interest is particularly in estimating the parameters in the structural component of the model. In a second simulation study, the relationships between the person parameters and the tests of multivariate hypotheses using the Bayes factor and the DIC are explored. Finally, the results from real-data examples are given and a few suggestions for extensions of the model are presented.
2. A Multivariate Multilevel Model
Various sources contribute to the variation between responses and RTs on test items. The total variation can be partitioned into variation due to (i) the sampling of persons and items, (ii) the nesting of responses within persons and items, and (iii) the nesting of persons within groups.
Two measurement models describe the distributions of the binary responses and continuous RTs at level 1 of the framework. At level 2, two correlation structures are posited to allow for the dependencies between the level 1 model parameters. First, the person parameters for ability and speed, denoted as θ} and ζ, respectively, are modeled to have a multivariate normal regression on covariates x, while group differences between these parameters are explained as a function of group-level covariates w at a third level. By specifying a higher-level regression structure for these random person parameters, it becomes possible to partition their total variance into within-group and between-group components. As a result, we are able to draw inferences about the person parameters for different groups simultaneously. Second, a correlation structure for the item parameters in the two measurement models is specified.
The model can be used for various analyses. First, the analysis might focus on the item parameters; more specifically, the relationships between the characteristics of the items in the domain covered by the test. For example, we may want to know the correlation between the time intensity and difficulty parameters of the items. Second, the analysis could be about the structural relationships between explanatory information at the individual and/or group levels and the test takers’ ability and speed. For example, the variance components of the structural model help us to explore the partitioning of the variance of the speed parameters across the different levels of analysis. Third, the interest might be in the random effects in the model, e.g., to identify atypical individuals or groups with respect to their ability or speed.
2.1. Level-1 Measurement Models for the Responses and RTs
The probability of person i = 1, …, n j in group j = 1, …, J answering item k = 1, …, K correctly (y ijk = 1) is assumed to follow the three-parameter normal ogive model:
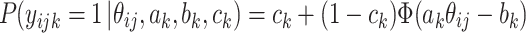 |
, where Φ(.) denotes the normal distribution function, ϑ ij the ability parameter of test taker ij, and a k, b k, and c k the discrimination, difficulty and guessing parameters of item k, respectively.
Typically, as the result of a natural lower bound at zero, RT distributions are skewed to the right. A family that describes this characteristic well is the log-normal distribution (van der Linden, 2006; Schnipke & Scrams, 1997). Let t ijk denote the log-response time of person i in group j on item k. We apply a normal model for t ijk, with a mean depending on the speed at which the person works, denoted as ζ ij, and the time intensity of the item, λ k. A higher λ k represents an item that is expected to consume more time. On the other hand, a higher ζ ij means that the person works faster and a lower RT is expected. A parameter ϕ k is introduced, which can be interpreted as a time discrimination parameter.
The response-time model at level 1 is given by:
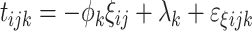 |
, where 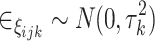 . Notice that the interpretation of the model parameters in (2) results in a different location of the minus sign compared to the IRT model. Also, there is a correspondence of the RT model with IRT models for continuous responses; for the latter, see, for instance, Mellenbergh (1994) and Shi & Lee (1998).
. Notice that the interpretation of the model parameters in (2) results in a different location of the minus sign compared to the IRT model. Also, there is a correspondence of the RT model with IRT models for continuous responses; for the latter, see, for instance, Mellenbergh (1994) and Shi & Lee (1998).
2.2. Multivariate Two-Level Model for the Person Parameters
The interest is in the relationships between the person parameters and the effects of potential explanatory variables. For convenience, we use the same set of explanatory variables for both types of person parameters; the generalization to the case of different variables is straightforward. Let x
j denote a known n
j × Q covariate matrix (with ones in the first column for the intercept) and 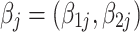 a Q × 2 matrix of regression coefficients for group j = 1, …, J. The coefficients are treated as random but they can be restricted to be common to all groups, leading to the case of one fixed effect.
a Q × 2 matrix of regression coefficients for group j = 1, …, J. The coefficients are treated as random but they can be restricted to be common to all groups, leading to the case of one fixed effect.
The regression of the two sets of person parameters at the individual level is defined by:
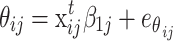 |
,
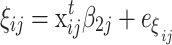 |
. The two sets of regression equations are allowed to have correlated error terms; 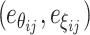 is taken to be bivariate normal with zero means and covariance matrix ΣP:
is taken to be bivariate normal with zero means and covariance matrix ΣP:
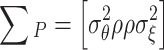 |
.
It is straightforward to extend the random effects model to explain variance in the β’s by group level covariates (Snijders & Bosker, 1999). For instance, test takers can be grouped according to their social economic background or because they are nested within different schools. Although different covariates can be included for the Q intercept and slope parameters, for convenience, it will be assumed that the same covariate matrix is used for β 1 and β 2. The covariates for the Q parameters of group j are contained in a matrix w j of dimension Q × S. That is, in total there are S covariates for each group, including the ones for the intercepts. The random effects β 1j and β 2j are then modeled as:
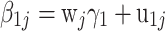 |
,
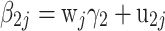 |
, where γ
1 and γ
2 are the vectors of regression coefficients of length S. The group-level error terms, (u
1j,u
2j), are assumed to be multivariate normally distributed with means zero and covariance matrix V. More stable parameter estimates can be obtained by restricting this covariance matrix to be block-diagonal with diagonal matrices V
1 and V
2, each of dimension Q × Q. In this case, the random effects in the regression of θ on x are allowed to correlate but they are independent of those in the regression of ζ on x. This choice will be made throughout this paper. Note that when 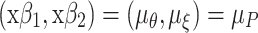 , the model as proposed by van der Linden (2008) is obtained as a special case.
, the model as proposed by van der Linden (2008) is obtained as a special case.
Let θ j and ζ j denote the vectors of length n j of the person parameters of group j. The entire structural multivariate multilevel model can now be presented as:
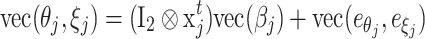 |
,
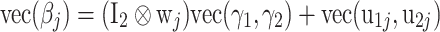 |
, where vec denotes the operation of vectorizing a matrix. We refer to these two models as level 2 and 3 models, respectively. Marginalizing over the random regression effects in (8) and (9), the distribution of vec(θ j, ζ j) becomes
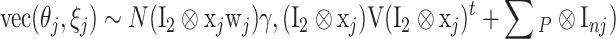 |
.
The structural component of the model allows a simultaneous regression analysis of all person parameters on explanatory variables at the individual and group levels while taking into account the dependencies between the individuals within each group. As a result, among other things, conclusions can be drawn as to the size of the effects of the explanatory variables on the test takers’ ability and speed as well as the correlation between these person parameters. Note that hypotheses on these effects can be tested simultaneously.
2.3. Multivariate Model for the Item Parameters
An empirical distribution for the item parameters is specified such that for each item the vector ζ k = (a k, b k, ϕ k, λ{itk}) is assumed to follow a multivariate normal distribution with mean vector μ I = (μ a, μ b, μ ϕ, μ{itλ})}:
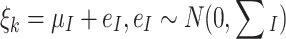 |
, where Σ I specifies the covariance structure.
The assumption introduces a correlation structure between the item parameters. For example, it may be expected that easy items require less time to be solved than more difficult items. If so, the time intensity parameter correlates positively with the item difficulty parameter. The guessing parameter of the response model has no analogous parameter in the RT measurement model (since there is no guessing aspect for the RTs). Therefore, it does not serve a purpose to include it in this multivariate model and an independent prior for this parameter is specified below.
3. Exploring the Multivariate Normal Structure
The observed response data are augmented using a procedure that facilitates the statistical inferences. Besides, as will be shown in the next section, these augmentation steps allow for a fully Gibbs sampling approach for estimation of the model.
First, an augmentation step is introduced according to Beguin & Glas (2001). A variable s ijk = 1 when a person ij knows the correct answer to question k and is s{itijk} = 0 otherwise. Its conditional probabilities are given by:
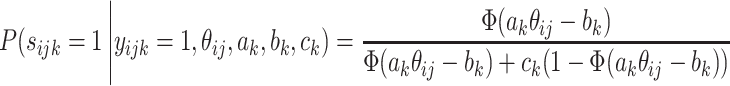 |
,
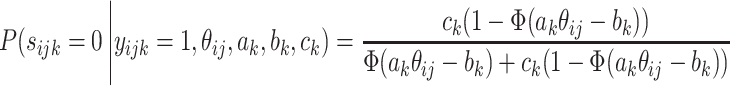 |
,
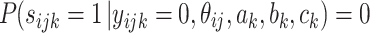 |
,
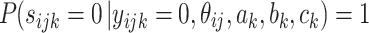 |
. Second, following Albert (1992), continuous latent responses z ij k are defined:
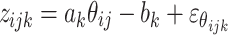 |
, where the error terms are standard normally distributed and s is taken to be a matrix of indicator variables for the events of the components of z being positive. When the guessing parameters are restricted to be zero, it follows immediately that s ijk = y ijk with probability one and the 2-parameter IRT model is obtained.
Statistical inferences can be made from the complete data due to the following factorization:
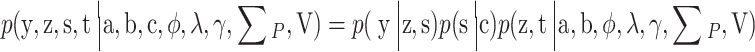 |
. Our interest is in exploring the structural relationships between ability and speed. Therefore, the term on the far right-hand side of (17) will be explored in more detail now. This likelihood can be taken to be that of a normal multivariate multilevel model,
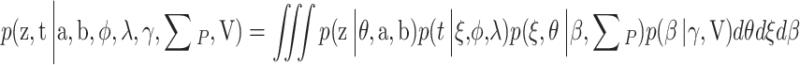 |
. Therefore, all factors in this decomposition are multivariate normal densities. The first two factors occur because of the independence of the responses and response times given the latent person parameters. The last two factors represent levels 2 and 3 of the model.
Inference from this multivariate hierarchical model simplifies when taking advantage of some of the properties of the multivariate normal distribution. For example, let us assume for a moment that the item parameters are fixed and known and define 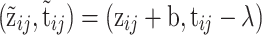 . Levels 1 and 2 of the model can then be represented by the following multivariate hierarchical structure:
. Levels 1 and 2 of the model can then be represented by the following multivariate hierarchical structure:  . (19) This representation provides insight in the complex correlational structure hidden in the data and entails several possible inferences. It also helps us to derive some of the conditional posterior distributions for the Gibbs sampling algorithm (e.g., the conditional posterior distributions of the latent person parameters given the augmented data). For a general treatment of the derivation of conditional from multivariate normal distributions, see, for instance, Searle, Casella, and McCulloch (1992).
. (19) This representation provides insight in the complex correlational structure hidden in the data and entails several possible inferences. It also helps us to derive some of the conditional posterior distributions for the Gibbs sampling algorithm (e.g., the conditional posterior distributions of the latent person parameters given the augmented data). For a general treatment of the derivation of conditional from multivariate normal distributions, see, for instance, Searle, Casella, and McCulloch (1992).
Parameter ρ, which controls the covariance between the θ s and ζ s, plays an important role in the model. It can be considered to be the bridge between the separate measurement models for ability and speed. Therefore, its role within the hierarchical structure will be explored in more detail.
The conditional covariance between the latent response variables and RTs on items k = 1, …, K is equal to 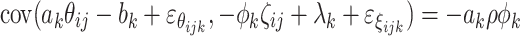 , due to independence between the residuals as well as the residuals and the person parameters. Since a
k and ϕ
k are positive, the latent response variables and RTs, and hence the responses and RTs, correlate negatively when ρ is positive. So, in spite of conditional independence between the responses and RTs given the person parameters, their correlation is negative.
, due to independence between the residuals as well as the residuals and the person parameters. Since a
k and ϕ
k are positive, the latent response variables and RTs, and hence the responses and RTs, correlate negatively when ρ is positive. So, in spite of conditional independence between the responses and RTs given the person parameters, their correlation is negative.
The conditional distribution of θ ij given ζ ij is normal:
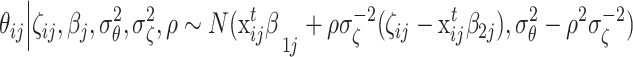 |
. A greater covariance ρ between the person parameters gives a greater reduction of the conditional variance of θ ij given ζ ij. The expression also shows that the amount of information about θ ij in ζ ij depends both on the precision of measuring the speed parameter and its correlation with the ability parameter.
From (19), it also follows that the conditional expected value of θ ij given the complete data is equal to
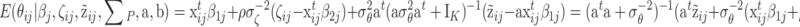 |
. The conditional expected value of θ ij consists of two parts: one part representing the information about θ ij in the (augmented) response data and another the information through the multivariate regression on x ij. For ρ = 0, (21) reduces to
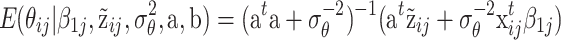 |
. This expression can be recognized as the precision-weighted mean of the predictions of θ ij from the (augmented) response data and from the linear regression of θ on x (see, for instance, Fox & Glas, 2001). Comparing (22) with (21), it can be seen that when ρ > 0, the expected value of θ ij increases for test takers who work at a greater than average speed; that is, a test taker’s ability is predicted to be higher when the same response pattern is obtained at a higher speed (i.e., in a shorter expected time on the same set of items).
In (19), in addition to the responses and RTs, the random test takers were the only extra source of heterogeneity. But another level of heterogeneity was added in (9), where the test takers were assumed to be nested within groups and the regression effects were allowed to vary randomly across them. Also, the item parameters correlate in (11). Because of these random effects and correlations, the marginal covariances between the measurements change.
We conclude this discussion with the following comments:
In (19), a special structure (compound symmetry) for the covariance matrix of the residuals at the level of individuals was shown to exist. This structure may lead to more efficient inference. For a general discussion of possible parameterizations and estimation methods for multivariate random effects structures, see, for instance, Harville (1977), Rabe-Hesketh and Skrondal (2001), and Reinsel (1983).
Linear multivariate three-level structures for continuous responses are discussed, among others, in Goldstein (2003), and Snijders and Bosker (1999). As already indicated, the covariance structure of the level-3 random regression effects is assumed to be block diagonal. This means that the parameters in the regression of θ on x are conditionally independent of those in the regression of ζ on x. It is possible to allow these parameters to correlate but this option is unattractive when the dimension of the covariance matrix becomes large. Typically, the covariance matrix is then poorly estimated (Laird & Ware, 1982).
For the same reason, the covariance matrix of the fixed effects in (9) is assumed to be block diagonal. The Bayesian approach in the next sections allows us to specify different levels of prior information about this matrix.
4. Bayesian Estimation Using Gibbs Sampling
In Bayesian statistics, inferences are made from the posterior distribution of the model parameters. Markov chain Monte Carlo (MCMC) methods enable us to simulate random draws from this distribution. Summary statistics can then be used to estimate the parameters or functionals of interest. A useful feature of MCMC methods is that they remain straightforward and easy to implement when the complexity of the model increases. Also, they allow for the simultaneous estimation of all model parameters. Since the current model is quite complex and has many parameters, we need these advantages to estimate the model. For a general introduction to Gibbs sampling, see Gelman, Carlin, Stern, and Rubin (2004) and Gelfand & Smith (1990). MCMC methods for IRT models are discussed by Albert (1992) and Patz & Junker (1999).
A new Gibbs sampling scheme was developed to deal with the extension of the model. Further, the scheme differs from that in van der Linden (2008) by its increased efficiency; it samples both types of person parameters in one step, taking into account the identifying restrictions, and avoids an MH step in the sampling of the item parameters due to better capitalization on the regression structure of the model. The full conditional distributions of all model parameters for the scheme are given in the Appendix.
The remainder of this section discusses the priors and identifying restrictions we use.
4.1. Prior Distributions
The parameter c k is the success probability in the Binomial distribution for the number of correct guesses on item k. A Beta prior with parameters B(b′1, b′2) is chosen, which is the conjugate for the Binomial likelihood, and thus leads to a Beta posterior.
For the residual variance τ 2k, a conjugate inverse Gamma prior is assumed with parameters g 1 and g 2.
A normal inverse-Wishart prior is chosen for the mean vector μ I and covariance matrix Σ I of the item parameters. The family of priors is conjugate for the multivariate normal distribution (Gelman et al., 2004). Thus,
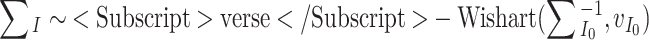 |
,
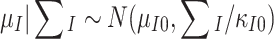 |
. A vague proper prior follows if ν I0 is set equal to the minimum value for the degrees-of-freedom parameter and a diagonal variance matrix with large values is chosen.
Likewise, a normal inverse-Wishart prior is chosen for the fixed parameters γ of the multivariate random-effects structure of the person parameters in (9),
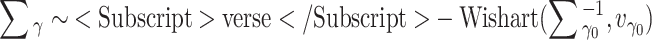 |
,
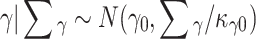 |
.
The covariance matrix V of the level-3 random group effects (u 1j,u 2j) is assumed to also have an inverse-Wishart prior with scale matrix V 0 and degrees of freedom ν V 0.
The prior for the covariance matrix of the person parameters, Σ P, is chosen to give special treatment because the model is not yet identified.
4.2. Prior for ΣP with Identifying Restrictions
The model can be identified by fixing the scales of the two latent person parameters. A straightforward way of fixing the scale of the ability parameter is to set the mean equal to zero and the variance to one. To avoid a tradeoff between ϕ and ζ the time discrimination parameters are restricted to 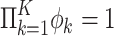 . When these are restricted to ϕ = 1 the lognormal RT model as proposed by van der Linden (2006) is obtained. Then for the speed parameter, since RTs have a natural unit, we only have to fix the origin of its scale and set it equal to its population mean. Note that a multivariate probit model is identified by fixing the diagonal elements of the covariance matrix (Chib & Greenberg, 1998) but that because of the special nature of the RTs, in the current case only one element of Σ
P has to be fixed.
. When these are restricted to ϕ = 1 the lognormal RT model as proposed by van der Linden (2006) is obtained. Then for the speed parameter, since RTs have a natural unit, we only have to fix the origin of its scale and set it equal to its population mean. Note that a multivariate probit model is identified by fixing the diagonal elements of the covariance matrix (Chib & Greenberg, 1998) but that because of the special nature of the RTs, in the current case only one element of Σ
P has to be fixed.
Generally, two issues arise when restricting a covariance structure. First, defining proper priors for a restricted covariance matrix is rather difficult. For example, for the conjugate inverse-Wishart prior, there is no choice of parameter values that reflects a restriction on the variance of the ability parameter such as that above. For the multinomial probit model, McCulloch and Rossi (1994) tackled this problem by specifying proper diffuse priors for the unidentified parameters and reporting the marginal posterior distributions of the identified parameters. However, it is hard to specify prior beliefs about unidentified parameters. Second, for a Gibbs sampler, sampling from a restricted covariance matrix requires extra attention. Chib and Greenberg (1998) defined individual priors on the free covariance parameters, but as a result, the augmented data had to be sampled from a special truncated region and the values of the free covariance parameter could only be sampled using an MH step. However, such steps involve the specification of an effective proposal density with tuning parameters that can only be fixed through a cumbersome process. A general approach for sampling from a restricted covariance matrix can be found in Browne (2006) but this is also based on an MH algorithm.
Here, a different approach is taken that allows us to specify proper informative priors and facilitate the implementation of the Gibbs sampler. A prior is chosen such that σ 2θ = 1 with probability one. Hence, covariance matrix Σ P always equals:
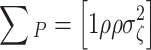 |
. Using (8) and (27), the conditional distribution of ζ ij given θ ij has density
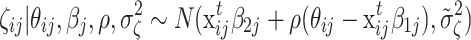 |
where 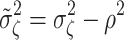 . Parameter ρ can be viewed as the slope parameter in a normal regression problem of ζ
ij on θ
ij with variance
. Parameter ρ can be viewed as the slope parameter in a normal regression problem of ζ
ij on θ
ij with variance 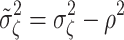 . Specifying a normal and inverse gamma as conjugate priors for these parameters,
. Specifying a normal and inverse gamma as conjugate priors for these parameters,
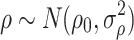 |
,
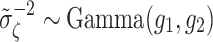 |
, their full conditional posterior distributions become
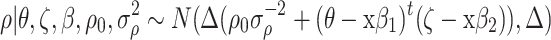 |
,
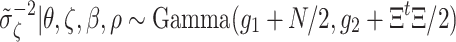 |
, where
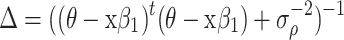 |
and
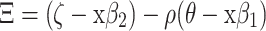 |
.
Since 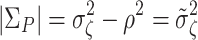 and
and 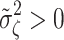 , it follows that the determinant |Σ
P | > 0. The latter is sufficient to guarantee matrix Σ
P to be positive semi-definite.
, it follows that the determinant |Σ
P | > 0. The latter is sufficient to guarantee matrix Σ
P to be positive semi-definite.
When implementing a Gibbs sampler, the random draws of the elements of covariance matrix Σ P in (27) can be constructed from the samples drawn from (30)–(31). These draws will show greater autocorrelation due to this new parametrization. This implies that more MCMC iterations are needed to cover the support of the posterior distribution adequately, a measure that only involves a (linear) increase in the running time of the sampler. On the other hand, convergence of the algorithm is easily established without having to specify any tuning parameter. Finally, this procedure also enables straightforward implementation of the data augmentation procedure since the zs can be drawn from a normal distribution truncated at zero, where s indicates when z is positive.
The key element of the present approach is the specification of a proper prior distribution for the covariance matrix with one fixed diagonal element and the construction of random draws from the matrix from the corresponding conditional posterior distribution. For the multinomial probit model, the approach was also followed by McCulloch, Polson, and Rossi (2000). For completeness, we also mention an alternative approach. Barnard, McCullogh, and Meng (2000) formulated a prior directly for the identified parameters. In order to do so, they factored the covariance matrix into a diagonal matrix with standard deviations and a correlation matrix, and specified an informative prior for the latter. This prior was then incorporated into a Griddy-Gibbs sampler. However, such algorithms can be slow and require the choices of a grid size and boundaries. Boscardin and Zhang (2004) followed a comparable approach but used a parameter-extended MH algorithm for sampling values from the conditional distribution of the correlation matrix.
5. Model Selection Methods
A model comparison method is often based on a measure of fit and some penalty function based on the number of free parameters for the complexity of the model. A bias-variance tradeoff exists between these two quantities since a more complex model often leads to less bias but a less complex model involves more accurate estimation. Two well-known criteria of model selection based on a deviance fit measure are the Bayesian information criterion (BIC) (Schwarz, 1978) and Akaike’s information criterion (AIC) (Akaike, 1973). These criteria depend on the effective number of parameters in the model as a measure of model complexity. A drawback of these measures is that they are often difficult to calculate for hierarchical models: Although the nominal number of parameters follows directly from the likelihood, the prior distribution imposes additional restrictions on the parameter space and reduces its effective dimension. In a random-effects model, the effective number of parameters depends strongly on the higher-level variance parameters. When the variance of the random effects approaches zero, all random effects are equal and the model reduces to a simple linear model with one mean parameter. But when the variance goes to infinity, the number of free parameters approaches the number of random effects.
Spiegelhalter et al. (2002) proposed the deviance information criterion (DIC) for model comparison when the number of parameters is not clearly defined. The DIC is defined as the sum of a deviance measure and a penalty term for the effective number of parameters based on a measure of model complexity described below.
An alternative method for model selection that can handle complex hierarchical models is the Bayes factor; for a review, see Kass and Raftery (1995). The Bayes factor is based on a comparison of marginal likelihoods but its implementation is hampered by its critical dependence on the prior densities assigned to the model parameters. It is known that the Bayes factor tends to favor models with reasonably vague proper priors; see, for instance, Berger and Delampady (1987) and Sinharay and Stern (2002). An advantage of the Bayes factor is its clear interpretation as the change in the odds in favor of the model when moving from the prior to the posterior distribution (Lavine & Schervish, 1999).
In one of the empirical examples below, the focus is on the structural multivariate model for the person parameters. It will be shown that a DIC can be formulated for choosing between models that differ in the fixed and/or random part of the structural model. In addition, a Bayes factor for selecting between the IRT measurement model for binary responses and the model extended with the hierarchical structure for responses and RTs is presented.
5.1. Model Selection Using the DIC
The DIC requires a closed-form likelihood. Our interest is focused on the likelihood of the structural parameters in the model; accordingly, all random effect parameters can be intregated out. Besides, the variances, covariances, and items parameters are considered as nuisance parameters, and their values are assumed to be known. So, a DIC will be derived for the complete-data likelihood with the random effects integrated out. Subsequently, the posterior expectation of the DIC over the augmented data will be taken. The same procedure was proposed for mixture models by DeIorio and Robert (2002).
Let z *ij = vec(z ij + b, t ij − λ) and H P = (a⊕−ϕ). From (19), Conditional on s, the measurement models for ability and speed can be summarized as
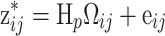 |
, where e
ij ∼ N(0,C), with 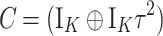 a diagonal matrix with in the left upper square 1 and in the right lower square τ on its diagonal, and Ω
ij = vec(θ
ij, ζ
ij). The focus is on the structure of Ω. Using the factorization in (17), the standardized deviance is
a diagonal matrix with in the left upper square 1 and in the right lower square τ on its diagonal, and Ω
ij = vec(θ
ij, ζ
ij). The focus is on the structure of Ω. Using the factorization in (17), the standardized deviance is
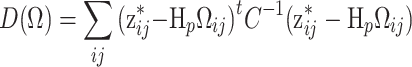 |
. The DIC is defined as
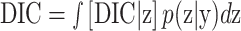 |
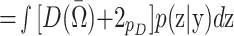 |
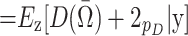 |
, where 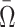 equals the posterior mean and p
D is the effective number of parameters given the augmented data. The latter can be shown to be equal to the mean deviance minus the deviance of the mean. Hence,
equals the posterior mean and p
D is the effective number of parameters given the augmented data. The latter can be shown to be equal to the mean deviance minus the deviance of the mean. Hence,
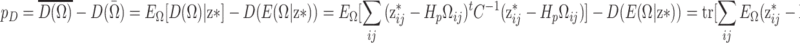 |
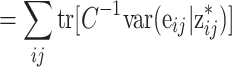 |
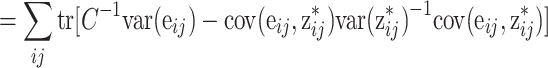 |
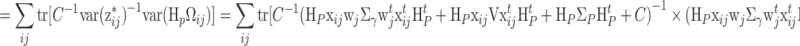 |
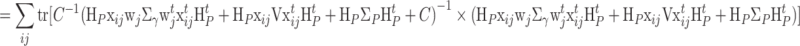 |
, where tr(·) denotes the trace function, i.e., the sum of the diagonal elements. The expectation is taken with respect to the posterior distribution of Ω. The terms in (38) can be recognized as the posterior variances of the residuals whereas those in (40) follow from the fact that because of independence, the variance of z *ij equals the sum of the variance of H P Ω ij and e ij.
DICs of nested models are computed by restricting one or more variance parameters in (41) to zero. Also, (41) can be estimated as a by-product of the MCMC algorithm; that is, the output of the algorithm can be used to estimate the posterior means of the model parameters in the second term of (37) and to integrate the DIC over the item parameters to obtain the first term. (In the current application, the item parameters are the nuisance parameters.)
Usually the variance parameters are unknown. Then the DIC has to be integrated over their marginal distribution, too. In fact, the correct Bayesian approach would be to integrate the joint posterior over the nuisance parameters to obtain the marginal posterior of interest. However, this approach is not possible since no closed-form expression of the DIC can be obtained for this marginal posterior. Thus, our proposal does not account for the unknown variances. Equation (41) reflects the effective number of parameters of the proposed model without the additional variability in the posterior because of the unknown covariance parameters. The more general case with unknown covariance parameters is complex, and no simple correction seems available. But Vaida and Blanchard (2005) showed that for a mixed-effects model, the correction for unknown covariance parameters is negligible asymptotically. So, it seems safe to assume that their effect on the estimate of (37) becomes only apparent when the covariance parameters are estimated less precisely.
5.2. Model Selection Using the Bayes Factor
The question we address is if the use of the RTs in the hierarchical model proves to be beneficial for making inferences about the ability parameter. As no benefits can be obtained when the correlation r(θ, ζ) = ϱ = 0 (i.e., independence between θ and ζ), a Bayes factor is defined to test whether the data support fitting a model M 1 between θ and ζ or the null model M 0 ⊂ M 1 with independence. For an introduction to Bayes factors, see Berger and Delampady (1987), Kass and Raftery (1995).
Both models are given equal prior weight. Therefore, the Bayes factor can be presented as
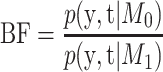 |
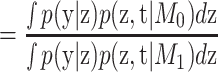 |
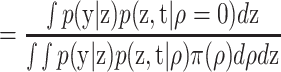 |
. A popular family of conjugate priors for the correlation coefficient has the form (1 − ϱ 2)ν on its support, 0 ≤ ϱ ≤ 1 (Lee, 2004). For ν = 0, a uniform distribution is obtained. For ν = 5, half-normal distribution is approximated. For ν→∞, the prior assigns probability 1 to ϱ = 0, which yields model M 0. To assess the sensitivity of the Bayes factor to the specification of the prior density, a variety of members from the family can be chosen.
6. Simulation Study
In the first study, different data sets were simulated and the parameters were re-estimated to check the performance of the Gibbs sampler. In the second study, the properties of the proposed Bayes factor in (44) were investigated for datasets generated for different values of ϱ and different choices of prior distributions.We also checked the rejection region for the null hypothesis. In the third study, the characteristics of the proposed DIC test were analyzed.
6.1. Parameter Recovery
Datasets were simulated for the following structural component of the model:
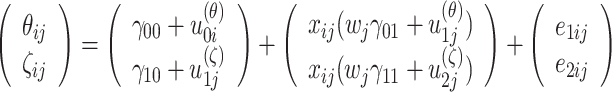 |
, where e ij ∼ N(0,Σ P), u (θ) ∼ N(0,V 1) and u (ζ) ∼ N(0,V 2). The model had the same set of explanatory variables in the regression of each latent parameter and had random intercepts and slopes. The intercepts and slopes were taken to be independent of the residuals and across the person parameters. The true values of the structural parameters used in the study are given in Table 1. The values of the explanatory variables x and w were drawn from a standard normal distribution. For the responses, the 2PL model was assumed and the item parameters were drawn from a multivariate normal distribution with mean μ I = (1, 0, 1, 0) and a diagonal covariance matrix Σ I with all variances equal to 0.5. Negative values of ϕ and a were simply ignored. Responses and RTs were simulated for N = 1,000 persons nested in 50 groups each taking 20 items.
Table 1.
Simulated and estimated values of the structural parameters.
| True value | EAP | SD | ||
|---|---|---|---|---|
| Fixed parameters | ||||
| γ00 | 0.00 | 0.00 | – | |
| γ01 | 4.00 | 3.77 | 0.23 | |
| γ10 | 0.00 | 0.00 | – | |
| γ11 | 3.00 | 2.99 | 0.12 | |
| Variance components | ||||
| ΣP | Σ11 | 1.00 | 1.00 | – |
| σ12 | 0.50 | 0.55 | 0.04 | |
| Σ22 | 1.00 | 1.07 | 0.06 | |
| V1 | V 11 | 1.00 | 1.00 | 0.25 |
| V 12 | 0.50 | 0.48 | 0.22 | |
| V 22 | 1.00 | 1.13 | 0.35 | |
| V2 | V 11 | 1.00 | 1.07 | 0.23 |
| V 12 | 0.50 | 0.47 | 0.17 | |
| V 22 | 1.00 | 0.86 | 0.19 | |
In the estimation procedure, the following hyperparameters were used: Scale matrices Σ I0 and Σ γ0 were chosen to be diagonal with elements 0.01 to indicate vague proper prior information, and we set μ I0 = (1, 0, 1, 0) and γ 0 = 0. Besides, a vague normal prior with parameters μ ρ = 0 and σ 2ρ = 10 was specified for ρ.
The MCMC procedure was iterated 50,000 times and the first 5,000 iterations were discarded when the means and posterior standard deviations of the parameters were estimated.
The accuracy of the parameter estimates was investigated by comparing them to their true values. The results for the parameters in the structural model are given in Table 1. Both the estimates of the fixed parameters and the variance components are in close agreement with the true values. (Note that γ 00 and γ 10 are zero due to the identifying restrictions.) Although not shown here, the same close agreement was observed for the item parameter estimates.
6.2. Sensitivity of the Bayes Factor
Usually, we will have little prior information about the correlation of the person parameters. Therefore, it is important to know how the Bayes factor behaves for a relatively vague prior distribution of the correlation 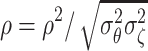 . In total, 500 data sets were simulated for different values of ϱ ∈ [0, 1] and an empty structural model for the person parameters. All other specifications were identical to those in the preceding study. The Bayes factor in (44) was calculated using an importance sampling method (Newton & Raftery, 1994). For each dataset, the calculations were repeated for different priors for the correlation parameter.
. In total, 500 data sets were simulated for different values of ϱ ∈ [0, 1] and an empty structural model for the person parameters. All other specifications were identical to those in the preceding study. The Bayes factor in (44) was calculated using an importance sampling method (Newton & Raftery, 1994). For each dataset, the calculations were repeated for different priors for the correlation parameter.
Following Lee (2004), a reference prior for ϱ was used, which led to
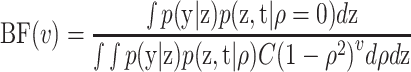 |
, with C the normalizing constant. According to Jefreys’ scheme (Kass & Raftery, 1995), 1/BF(ν) > 3 implies evidence against the null hypothesis of ϱ = 0 given the value of ν.
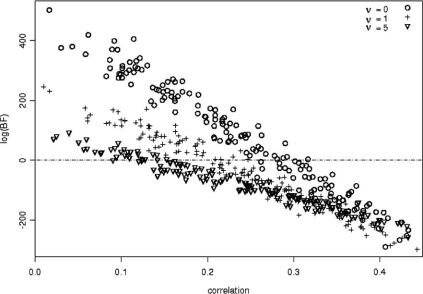
The results are shown in Fig. 1, where the dotted line indicates log(BF) = 0. For true values of ϱ close to zero or larger than 0.35, the Bayes factor yielded the same conclusion for all chosen priors. More specifically, it favored the null model for all values of ϱ below 0.1 but the alternative model for all values larger than 0.35. It can also be seen that the estimated Bayes factors are higher (and thus favor the null model more frequently) for lower values of ν, which correspond to the less informative priors. For ϱ ∈ [0.20, 0.35], the prior distribution of ϱ was the major determinant of the Bayes factor favoring the null or the alternative model.
Figure 1.
Log(BF) as a function of the correlation between accuracy and speed for 3 different priors for ϱ
It can be concluded that the Bayes factor is sensitive to the prior choice for ϱ. Figure 1 gives a clear idea about the variation of the Bayes factor for a class of prior distributions. This information can be used in real-world applications when a prior for ϱ needs to be selected but the information about this parameter is poor.
6.3. Iterative Model Building Using the DIC
In this study, it was investigated whether the DIC can be used to choose between models with different fixed and/or random terms in the structural component of the model for the person parameters. Data were simulated for 1,000 persons nested in 20 groups each taking 20 items using a model that is explained below. The setup was the same as in the earlier parameter recovery study; the only difference was that w j was set equal to one for all j
Table 2 summarizes the calculations of the DIC for four different models. 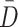 is the estimated posterior mean deviance;
is the estimated posterior mean deviance; 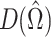 is the deviance for the posterior mean of the parameter values.
is the deviance for the posterior mean of the parameter values.
Table 2.
Deviance summaries for the four models in the simulation study.
| Model |
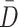
|
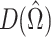
|
p D | DIC |
|---|---|---|---|---|
| 1, Two-level, fixed parameters | 40,168 | 38,184 | 1,984 | 42,152 |
| 2, Empty two-level | 40,161 | 38,194 | 1,967 | 42,129 |
| 3, Two-level+\gw \vb x | 40,172 | 38,206 | 1,966 | 42,139 |
| 4, Three-level + \gw \vb x | 40,165 | 38,290 | 1,875 | 42,039 |
Model 1 was an empty two-level model with fixed parameters for θ and ζ, which was obtained by setting ρ to 0 and the variances of each person parameters equal to 1,000. Model 2 was an empty two-level model that ignored any group structure for the test takers. In Model 3, the two-level structure was extended with a covariate of ζ and θ but no group structure was assumed. Model 4 was the true model under which the data were simulated; this model did have both the covariate and the group structure for the test takers. Identification of the models was obtained via the restriction 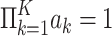 on the item parameters. This choice is motivated as follows: In Model 4, the variability of the person parameters is explained by V and the covariates. When estimating Model 1, 2, or 3 from the data simulated under Model 4, this variability should be captured by Σ
P as extra residual variation. Therefore, Σ
P was left unrestricted; otherwise, the variance would have been traded with the estimated a parameters, which might have led to misinterpretation of the results.
on the item parameters. This choice is motivated as follows: In Model 4, the variability of the person parameters is explained by V and the covariates. When estimating Model 1, 2, or 3 from the data simulated under Model 4, this variability should be captured by Σ
P as extra residual variation. Therefore, Σ
P was left unrestricted; otherwise, the variance would have been traded with the estimated a parameters, which might have led to misinterpretation of the results.
As expected, the DIC values we found suggested that Model 4 was best performing. Particularly, it can be seen that when the grouping of the test takers was ignored, this led to an increase in the effective number of parameters. Note that the optimal model choice is not necessarily the best fitting model, but a tradeoff between model fit and the number of parameters used.
7. Empirical Examples
In this section, two empirical examples illustrate the use of several developments that were presented in this paper.
7.1. First Example
A data set of 286 persons who had taken a computerized version of a 22-item personality questionnaire was analyzed. The respondents were Psychology and Social Sciences undergraduates from a university in Spain. The majority of the students was between 18 and 30 years old (age variable), and this group consisted of 215 girls and 71 boys (gender variable). The questionnaire consisted of two scales of 11 dichotomous items measuring neuroticism and extraversion. The neuroticism dimension assesses whether a person is prone to experience unpleasant emotions and is emotionally unstable and the extraversion dimension measures sociability, enthusiasm, and arousal of pleasure. According to the five factor model, these two dimensions summarize part of the covariation among personality traits.
As already indicated, because it does not assume anything about the relationship between the speed at which the individual test takers work and the latent trait represented in the response model, the modeling framework can also be applied to personality questionnaires. For this domain, it is also interesting to study the responses and RTs simultaneously. In addition to the statistical advantages of multivariate modeling of the data over separate univariate modeling, such a study would allow us to infer, for instance, how differences in speed levels between subgroups of test takers correlate with differences in their personality traits.
From earlier results, it was known that there is a moderate negative dependency between neuroticism and extraversion (Becker, 1999; McCrea & Costa, 1997). Here, interest was focused on the differences between students with respect to these two personality dimensions given age and gender. Additionally, variation in the respondent’s speed-levels with respect to neuroticism and extraversion was explored. This part of the study involved the estimation of the covariances between the personality traits and the latent speed-levels.
Since this test consisted of yes-no personality questions, the 2PL model was chosen as the measurement model for the responses. For the RTs, the measurement part was specified by (2). The following structural part was specified to explore the variation in speed and the traits as a function of both background variables:
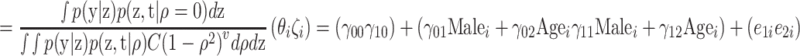 |
, where e ∼ N(0,Σ P). Further, γ 00 and γ 10 denote the intercepts, γ01 and γ11 represent the effects of being male, and γ 02 and γ 12 represent the effects of age. The age vector contained the age of the test takers on a continuous scale.
Four models were fitted to the data: (1) null model without covariates, (2) and (3) structural multivariate model with age and gender as a covariate, respectively, and (4) full structural multivariate model with both age and gender as covariates. For estimation, proper noninformative priors were specified, with all prior variance components set at 100 and the covariances at 0. The MCMC algorithm was iterated 50,000 times; the first 10,000 iterations were discarded as the burn-in period.
Posterior predictive checks were used to evaluate several assumptions of the model. An important assumption of the model is that of local independence. Therefore, an odds ratio statistic was used to test for possible dependencies between response patterns of items. For an impression of overall fit of the response model, an observed score statistic was estimated to assess if the model was able to replicate the observed score patterns. For a detailed description of these two statistics, see Sinharay (2005) and Sinharay, Johnson, and Stern (2006). To assess the fit of the RT model, van der Linden and Guo (2008) proposed a Bayesian residual analysis. That is, by evaluating the actual observation t
ik under the posterior density, the probability of observing a value smaller than t
ik can be approximated by 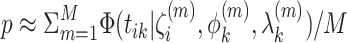 , from M iterations from the MCMC chain. According to the probability integral transform theorem, under a good fitting model, these probabilities should be distributed U(0, 1). Model fit can then be checked graphically by plotting the posterior p-values against their expected values under the U(0, 1) distribution.
, from M iterations from the MCMC chain. According to the probability integral transform theorem, under a good fitting model, these probabilities should be distributed U(0, 1). Model fit can then be checked graphically by plotting the posterior p-values against their expected values under the U(0, 1) distribution.
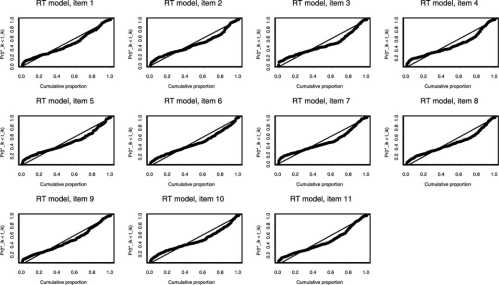
The posterior checks of the model were based on 1,000 replicated data sets from the posterior distribution. The fitted IRT model replicated the responses well, as the observed sum score statistic did not point at any significant flaws for neither of the two scales. The odds ratio statistic indicated that for two item combinations on the neuroticism scale and for four item combinations on the extraversion scale, a violation of local independence might exist. However, given all possible item combinations, these possible violations of local independence did not give any reason to doubt the unidimensionality of the scales. As indicated by minor deviations in de lower tail and in the middle of the U(0, 1) distributions, the RT model tended to slightly underpredict the quicker responses (see Fig. 2). Overall, however, model fit was satisfactory.
Figure 2.
Probabilities of P(t*ik < t ik|y, t) against their expected values under the U(0,1) distribution for the 11 items of the neuroticism scale, Example 2.
Table 3 gives the calculated DIC values for the four models and the two scales. Comparing the results for model (1) and model (3), the DIC criterium yielded no significant difference in performance between boys and girls on both scales. That is, for the neuroticism as well as the extraversion scale, no mean significant difference between boys and girls was found, neither in the latent personality traits, nor in the speed of working on the test. Neither did the age of the test takers explain any significant amount of variation in the personality traits and speed levels.
Table 3.
DIC values for 4 models fitted to the neuroticism and extraversion scales.
| Model | Neuroticism | Extraversion | ||||
|---|---|---|---|---|---|---|
| p D |
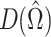
|
DIC | p D |
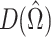
|
DIC | |
| 1 (null) | 572 | 3,839 | 4,983 | 572 | 3,767 | 4,911 |
| 2 (gender) | 572 | 3,846 | 4,990 | 572 | 3,774 | 4,918 |
| 3 (age) | 572 | 3,941 | 5,085 | 572 | 3,838 | 4,982 |
| 4 (full) | 572 | 3,943 | 5,087 | 572 | 3,827 | 4,971 |
Next, the respondents were clustered with respect to their estimated extraversion scores. The clustering was such that the intervals of respondents’ scores in each cluster had equal probability mass under a normal model for the population distribution. The sample size of 286 respondents allowed a grouping of respondents in eight different clusters of extraversion levels. Note that the clusters were obtained from an estimated population model, and that they jointly represented the entire score range.
It was investigated whether the grouping of respondents with respect to the extraversion scores explained any variation in respondents’ neuroticism scores. Further, the influence of the background variables was explored. The following multivariate random effects structural model was specified:
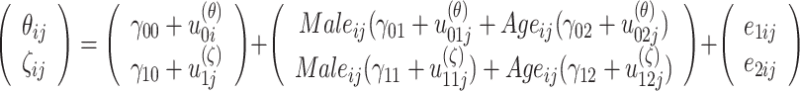 |
(47) |
, where e ij ∼ N(0,Σ P), u (θ) ∼ N(0,V 1) and u (ζ) ∼ N(0,V 2). In (47), the intercepts and slope coefficients for the regression on the neuroticism scores and the speed levels were treated as random across clusters of extraversion levels. These random effects were allowed to correlate both within the regression on the neuroticism scores and within the regression on the speed levels. Also, the error terms at the individual level were allowed to correlate since the speed levels and neuroticism scores were clustered within individuals.
Five models were fitted to the neuroticism scale by restricting one or more parameters to zero: (1) the null model with fixed intercepts by restricting V 1 and V 2 to be zero; (2) the empty multivariate random effects model (without covariates) with free covariance parameters; (3)–(4) a multivariate random effects model including a random regression effect for gender and age, respectively, and (5) the full model as specified in (47).
Using the proper noninformative priors described earlier, the models were estimated using 50,000 iterations of the Gibbs sampler, where 10,000 iterations were discarded because of the burn-in. The DIC value for each of the five models was estimated using (36) since our interest was focused primarily on the structural model on the speed levels and neuroticism scores. The estimated DIC values are given in Table 4.
Table 4.
DIC values for five models fitted to the neuroticism scale, accounting for a grouping of respondents in extraversion levels.
| Model | p D |
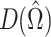
|
DIC |
|---|---|---|---|
| 1 (null) | 572 | 3,839 | 4,983 |
| 2 (empty) | 521 | 3,858 | 4,899 |
| 3 (gender) | 536 | 3,866 | 4,938 |
| 4 (age) | 572 | 3,860 | 5,004 |
| 5 (full) | 572 | 3,873 | 5,017 |
It can be seen that the empty multivariate random-effects model had a smaller effective number of model parameters relative to the null model and was to be preferred given the DIC values of both models. The estimated deviance increased slightly for models 3–5, which can be attributed to additional sampling variance introduced by the covariates. Note that in the empty multivariate random-effects model, the individual random-effect parameters were modeled as group-specific random effects at the level of the clusters of extraversion scores (a third level in the model) and that this led to a serious reduction in the effective number of model parameters. It can be concluded that the grouping of respondents according to their extraversion levels explained a substantial amount of variation in the speed levels as well as the neuroticism scores. The estimated correlation between the neuroticism scores and the speed levels was 0.30 (with a standard deviation of 0.07), which justified the multivariate modeling approach. Intraclass correlation coefficients were calculated to asses the amount of variability in the individual neuroticism scores and the speed levels due to the grouping of respondents in clusters of extraversion levels. The intraclass correlation estimates for neuroticism and the speed trait were based on the MCMC output for the empty multivariate random effects model. The estimates were
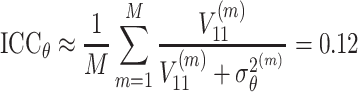 |
,
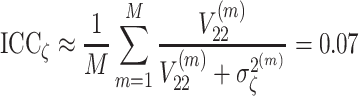 |
, where m = 1, …, M denotes the number of iterations after burn-in. It follows that 12% of the variability in the neuroticism trait could be explained by the grouping of the respondents by their extraversion levels. It is surprising that 7% of the variability in speed levels was located at the group level. This means that the clustering of the respondents via the estimated extraversion levels explained a significant amount of variation in the individual speed levels corresponding to the neuroticism test. The explanation is supported by the estimated correlation between both speed parameters, which was 0.76. Note that this relatively high correlation between the individual speed levels on the two tests also supports the assumption of stationary speed during testing. Finally, the DIC values show that the covariates did not explain any variation in the trait or speed levels. It can be seen that the introduction of random regression parameters for the background variables did not lead to any reduction in the effective number of parameters since the covariates did not explain any variation within the grouped neuroticism scores. Neither did they for the entire sample of neuroticism scores.
7.2. Second Example
In this example, the data set studied earlier by Wise, Kong, and Pastor (2007) was analyzed. This data set included 388 test takers who each answered 65 items of a computer-based version of the Natural World Assessment Test (NAW-8). This test is used to assess the quantitative and scientific reasoning proficiencies of college students. It was part of a required education assessment for mid-year sophomores by a medium-sized university. Covariates for the test takers such as their SAT scores, gender (GE), a self-report measure of citizenship (CS) and a self-report measure of test effort (TE) were available. Citizenship was a measure of a test taker’s willingness to help the university collecting its assessment data, whereas test effort reflected the importance of the test to the test taker. The number of response options for the items varied between 2 and 6.
The 3PL model was chosen as the measurement model for the responses. In the estimation procedure, the same hyperparameter values as in the simulation study above were used to specify vague proper prior knowledge. The model was estimated with 20,000 iterations of the Gibbs sampler, and the first 10,000 iterations were discarded as the burn-in. The odds ratio statistic indicated that for less than 4% of the possible item combinations there was a significant dependency between two items. The replicated response patterns under the posterior distribution matched the observed data quite well, as shown by the observed sum score statistic. From the posterior residual check, it followed that the RT model described the data well. The estimated time discrimination parameters varied over [0.25, 1.65], indicating that the items discriminated substantially between test takers of different speed. This result was verified by testing the RT model with ϕ = 1 against the RT model where ϕ ≠ 1 using the DIC. The estimated DIC’s were 85,780 and 84,831 for the restricted and for the unrestricted RT model, respectively.
Table 5 gives the estimated covariance components and correlations between the level 1 parameters. The correlation between the person parameters was estimated to be −0.76. The Bayes factor for testing the null hypothesis of this correlation being zero, clearly favored the alternative for the range of possible priors given in the simulation study above. Therefore, for this data set, fitting the hierarchical model has to be favored over the alternative of independence between the two constructs. An explanation for this strong negative dependency might be that higher-ability candidates have more insight in their test behavior and, therefore, are better at time management. A negative correlation between speed and ability also often suggests a nonspeeded test, because it implies that higher ability test takers who take their time do not run out of time toward the end of the test.
Table 5.
Estimated covariance components and correlations.
| Variance components | EAP | SD | Cor | |
|---|---|---|---|---|
| Σp | Σ11 | 1.00 | – | 1.00 |
| Σ12 | −0.380 | 0.02 | −0.76 | |
| Σ22 | 0.25 | 0.02 | 1.00 | |
| Σ11 | 0.15 | 0.04 | 1.00 | |
| Σ12 | −0.110 | 0.04 | −0.53 | |
| Σ13 | 0.05 | 0.02 | 0.41 | |
| Σ14 | 0.02 | 0.04 | 0.09 | |
| Σ22 | 0.33 | 0.07 | 1.00 | |
| Σ23 | 0.06 | 0.03 | 0.34 | |
| Σ24 | 0.07 | 0.05 | 0.21 | |
| Σ33 | 0.10 | 0.02 | 1.00 | |
| Σ34 | 0.10 | 0.03 | 0.51 | |
| Σ44 | 0.35 | 0.06 | 1.00 | |
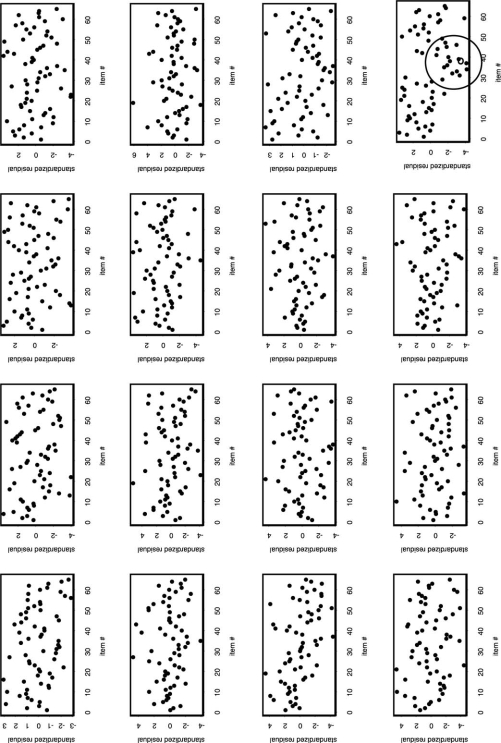
As shown earlier by van der Linden et al. (2007), response times can be a valuable tool for diagnosing differential speededness. Thereby, checks on the assumption of stationary speed during the test are particularly useful. For each test taker, the standardized residuals 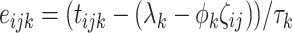 were calculated. When the stationary speed assumption holds, a test taker’s residual pattern shows randomly varying residuals which almost all will lie between [−2,2]. However, a test taker running out of time will show a deviation of this assumption toward the end of the test. In such a case, this result is misfit of the RT model, because of larger residuals for the test taker on these last items. In Fig. 3, residual patterns of the RT model for 16 test takers are shown. An aberrancy can be seen in the last figure, where for some items the test taker responded unusually fast. However, a graphical check of the residual patterns of all the test takers did not reveal any structural aberrancies. Therefore, there were no indications of speededness for this test.
were calculated. When the stationary speed assumption holds, a test taker’s residual pattern shows randomly varying residuals which almost all will lie between [−2,2]. However, a test taker running out of time will show a deviation of this assumption toward the end of the test. In such a case, this result is misfit of the RT model, because of larger residuals for the test taker on these last items. In Fig. 3, residual patterns of the RT model for 16 test takers are shown. An aberrancy can be seen in the last figure, where for some items the test taker responded unusually fast. However, a graphical check of the residual patterns of all the test takers did not reveal any structural aberrancies. Therefore, there were no indications of speededness for this test.
Figure 3.
Standardized residual patterns for the RT model for 16 selected test takers.
Subsequently, the following structural model on the person parameters was specified to identify possible relationships of ability and speed with the covariates:
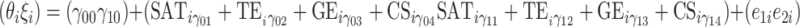 |
, where e i ∼ N(0,Σ P). Several hypotheses about this model were tested. First, the composite null hypothesis H 01 of both γ 01 and γ 11 equal zero was tested. Second, the null hypotheses H{ia02} that γ 02 and γ 12 equal zero were evaluated and, similarly, the hypotheses H 03 (γ 03 and γ 13 equal zero) and H 04 (γ 04 and γ 14 equal zero) were evaluated. Finally, by iterative model building, the composite hypothesis H 05 of the effects γ 03, γ04, γ 12, γ13 and γ14 equal to zero was tested. Testing these hypotheses corresponds to comparing models that differ only in their fixed part. This can be easily done via a Bayes factor because by using a result known as the Savage-Dickey density ratio (Dickey, 1971; Verdinelli & Wasserman, 1995), these Bayes factors are easy to obtain in reduced computation time.
The hypotheses that gender and citizenship had no effect on ability and speed were con- firmed. Also, the estimated 0.95 HPD regions of their effects (and their 0.90 HPD regions too) included 0, which was another indication that these covariates did not have any explanatory power in speed and ability. However, the SAT scores and test effort explained a significant amount of variation between the person parameters. This result implies the following reduced model:
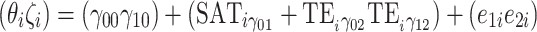 |
, where e i ∼ N(0,Σ P). The Bayes factors for the several nested models and the final estimates of the regression parameters are given in Table 6.
Table 6.
Estimated Bayes factors and regression parameters for the structural models.
| Hypothesis | log(BF) | |
|---|---|---|
| H01 | −5.0 | |
| H02 | −21.3 | |
| H03 | 16.4 | |
| H04 | 16.3 | |
| H05 | 16.2 | |
| Fixed parameters | EAP | SD |
| γ01 | 0.25 | 0.03 |
| γ02 | 0.25 | 0.03 |
| γ12 | −0.22 | 0.02 |
Intuitively, a positive relationship of TE with ability should have been expected. That is, test takers scoring higher on the TE-scale should have been expected to differ from test takers who care less about their results. Also, when the test is relatively more important to the candidate, he/she can be expected to try harder and spend more time on each item to get better results. The negative relationship of TE with speed is also in agreement with this hypothesis since a lower speed results in higher expected RTs. As expected, the SAT score shows a positive relationship with ability. However, there was no significant effect for SAT with respect to the speed of working of the test takers.
8. Discussion
A framework for a multivariate multilevel modeling approach was given in which the latent response parameters are measured using conjoint IRT models for the response and response time data. The IRT models for speed and ability are based on the assumption of conditional independence. This means that the ability parameter (speed parameter) is the assumed underlying construct for the response data (response time data). As a result, for each individual, at the level of measurements the responses and response times are local independent given the latent person parameters. The correlation structure between the person parameters is specified at a higher level. The correlation between speed and accuracy in the population of respondents can be tested via a Bayes factor. As the empirical examples showed, the correlation between ability and speed is not necessarily positive. The sign of this relationship will probably depend on the type of test and the test conditions. That is, sometimes hard work will pay off (e.g., a test with strict time limit) while for another setting “take your time” might be the best advice. RTs can give insight about the best strategy of test taking, which is useful information for both test takers and test developers. Other model selection issues related to the structural model on the person parameters can be handled via the proposed DIC which can be computed as a by product of the MCMC algorithm. It was shown that the MCMC algorithm performed well and enabled simultaneous estimation.
The class of multivariate mixture models has not received much attention in the literature. Schafer and Yucel (2002) developed an MCMC implementation for the linear multivariate mixed model with incomplete data that does converge rapidly for a small number of large groups but it is limited to two levels of nesting. Shah, Laird, and Schoenfeld (1997) extended the EM-algorithm of Laird and Ware (1982) to deal with linear bivariate mixed models. Also, for some applications, it may be possible to stack the columns of the response matrix and apply standard software for univariate mixed models (e.g., SAS Proc Mixture; S-Plus Nlme). However, this approach quickly becomes impossible when the number of individuals per group and/or the number of variables grows. The MCMC algorithm developed in this project, which is available in R from the authors upon request, may help researchers to analyze nonlinear multivariate multilevel mixed response data. This implementation is not limited to small numbers of variables or responses and can handle multiple random effects.
The model in this paper can easily be extended, for example, to deal with polytomous response data. MCMC algorithms for polytomous IRT models can be found in Fox (2005), Patz and Junker (1999), and Johnson and Albert (1999), among others. The necessary adjustment of the MCMC algorithm consists of replacing the random draws from the parameters in the threeparameter normal-ogive IRT model with those in a polytomous model. Although several studies have shown the log-normal model to yield satisfactory fit to RTs on test items, the hierarchical framework can be used with other measurement models for RTs, for example, to deal with RT distributions with a different skewed or that require heavier tails to be more robust against outliers.
If subpopulations of test takers follow different strategies to solve the items, differences in the joint distribution of accuracy and speed can be expected. To model them, a mixture modeling approach with different latent classes for different strategies can be used (see, for instance, Rost, 1990). This procedure can also be used to relate the popularity of different strategies to covariates.
Finally, the relationship between accuracy and speed may differ across groups of items, for instance, when they are organized in families of cloned items (Glas & van der Linden, 2003) or are presented with a testlet structure (Bradlow, Wainer, & Wang, 1999). In order to deal with such cases, the hierarchical framework has to be extended with a group structure for items. The consequences of this extension and the extensions above for the MCMC method of estimation and hypothesis testing still have to be explored.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Appendix: Gibbs Sampling Scheme
The Gibbs sampler iteratively samples from the full conditional distributions of all parameters. The full conditional distributions are specified below.
Sampling of Structural Model Parameters The sampling of the augmented data is described in (16).
As for the person parameters, observe that (19) can be written as
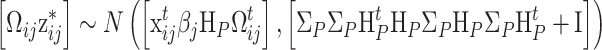 |
, where the matrix notation is the same as in (32), with z *ij = vec(z ij k + b k, t ijk − λ k) and H P = (a⊕−ϕ). From the fact that (50) is multivariate normal, it follows for the full conditional distribution of the person parameters that
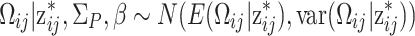 |
, with
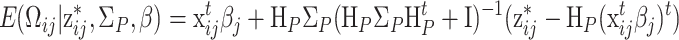 |
and
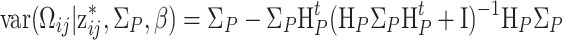 |
.
This result involves an efficient sampling scheme since the values of both person parameters are obtained in just one step.
The derivation of the full conditional distribution of regression coefficients β and γ is analogous. From (50) and (9), it follows that the β js are multivariate normal with mean
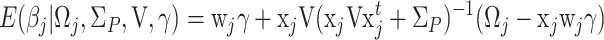 |
, and variance,
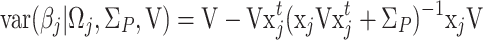 |
.
Likewise, from (9) and (26), the (fixed) coefficients γ are multivariate normal distributed with mean
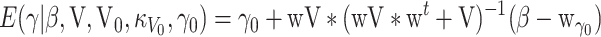 |
, and variance
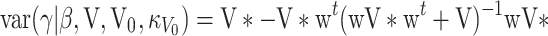 |
, where 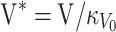 .
.
The full conditional distribution of covariance matrix Σ P was already introduced in the section on the identifying prior structure.
Sampling of Remaining Parameters As for the item parameters, a regression structure analogous to that of the person parameters in (19) can be found. Let Λk = (a k, b k, ϕ k, λ k)t and H I = (θ,−1 N) ⊕ (−ζ, 1 N). The item parameters are the coefficients of the regression of z *k on H I. Combined with the prior in (11), this observation leads to a multivariate normal posterior distribution of the item parameters with mean,
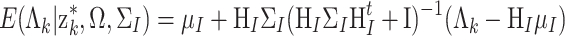 |
and variance,
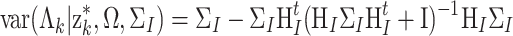 |
.
The parameters of the distribution of the item parameters follow a multivariate normal distribution; see (11). The normal inverse-Wishart prior in (23) and (24) is conjugate for the multivariate normal distribution (Gelman et al., 2004). The resulting posterior distribution also belongs to the normal inverse-Wishart family:
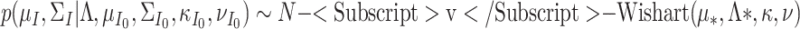 |
with parameters:
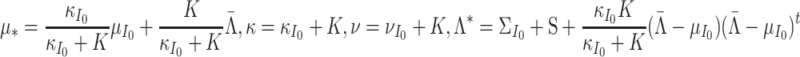 |
, where 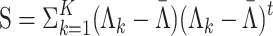 .
.
Likewise, for the fixed parameters γ, an Inverse-Wishart prior was specified. So, the posterior is an Inverse-Wishart
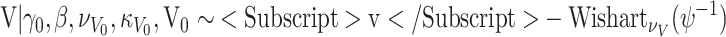 |
with parameters
 |
.
For the 3PL model, an additional augmentation step is introduced according to Beguin and Glas (2001). A variable s ijk = 1 when a person ij knows the correct answer to question k and is s ijk = 0 otherwise. Its conditional probabilities are given by (12). Subsequently, z ijk ∼ N(a kθij −b k, 1), truncated at the left of 0 when sijk = 0 and truncated at the right when s ijk = 1.
It was already noted that the posterior of the guessing parameters is a Beta distribution:
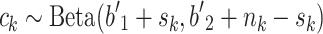 |
, where n k is the number of people who do not know the answer and s k is the number of people who guessed the answer correctly.
For the residual variance of the RT model τ
2k, with an Inverse-Gamma prior, the posterior is again an Inverse-Gamma distribution with parameter g
1 + N/2 and scale parameter 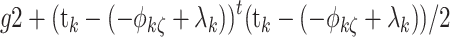 .
.
Footnotes
The authors thank Steven Wise, James Madison University, and Pere Joan Ferrando, Universitat Rovira i Virgili, for generously making available their data sets for the empirical examples in this paper.
References
- Akaike H. Information theory and an extension of the maximum likelihood principle. In: Petrov B.N., Csaki F., editors. 2nd international symposium on information theory. Budapest: Akademiai Kiado; 1973. pp. 267–281. [Google Scholar]
- Albert J.H. Bayesian estimation of normal ogive item response curves using Gibbs sampling. Journal of Educational Statistics. 1992;17:251–269. doi: 10.2307/1165149. [DOI] [Google Scholar]
- Barnard J., McCullogh R., Meng X.-L. Modelling covariance matrices in terms of standard deviations and correlations, with application to shrinkage. Statistica Sinica. 2000;10:1281–1311. [Google Scholar]
- Becker P. Beyond the big five. Personality and Individual Differences. 1999;26:511–30. doi: 10.1016/S0191-8869(98)00168-8. [DOI] [Google Scholar]
- Beguin A.A., Glas C.A.W. MCMC estimation and some model-fit analysis of multidimensional IRT models. Psychometrika. 2001;66:541–562. doi: 10.1007/BF02296195. [DOI] [Google Scholar]
- Berger J.O., Delampady M. Testing precise hypotheses. Statistical Science. 1987;2:317–352. doi: 10.1214/ss/1177013238. [DOI] [Google Scholar]
- Boscardin W.J., Zhang X. Modeling the covariance and correlation matrix of repeated measures. In: Gelman A., Meng X.-L., editors. Applied Bayesian modeling and causal inference from incomplete-data perspectives. New York: Wiley; 2004. pp. 215–226. [Google Scholar]
- Bradlow E.T., Wainer H., Wang X. A Bayesian random effects model for testlets. Psychometrika. 1999;64:153–168. doi: 10.1007/BF02294533. [DOI] [Google Scholar]
- Bridgeman B., Cline F. Effects of differentially time-consuming tests on computer-adaptive test scores. Journal of Educational Measurement. 2004;41:137–148. doi: 10.1111/j.1745-3984.2004.tb01111.x. [DOI] [Google Scholar]
- Browne W.J. MCMC algorithms for constrained variance matrices. Computational Statistics & Data Analysis. 2006;50:1655–1677. doi: 10.1016/j.csda.2005.02.008. [DOI] [Google Scholar]
- Chib S., Greenberg E. Analysis of multivariate probit models. Biometrika. 1998;85:347–361. doi: 10.1093/biomet/85.2.347. [DOI] [Google Scholar]
- DeIorio M., Robert C.P. Discussion of Spiegelhalter et al. Journal of the Royal Statistical Society, Series B. 2002;64:629–630. [Google Scholar]
- Dickey J.M. The weighted likelihood ratio, linear hypothesis on normal location parameters. The Annals of Mathematical Statistics. 1971;42:204–223. doi: 10.1214/aoms/1177693507. [DOI] [Google Scholar]
- Fox J.-P. Multilevel IRT using dichotomous and polytomous items. British Journal of Mathematical and Statistical Psychology. 2005;58:145–172. doi: 10.1348/000711005X38951. [DOI] [PubMed] [Google Scholar]
- Fox J.-P., Glas C.A.W. Bayesian estimation of a multilevel IRT model using Gibbs sampling. Psychometrika. 2001;66:269–286. doi: 10.1007/BF02294839. [DOI] [Google Scholar]
- Gelfand A.E., Smith A.F.M. Sampling-based approaches to calculating marginal densities. Journal of the American Statistical Association. 1990;85:398–409. doi: 10.2307/2289776. [DOI] [Google Scholar]
- Gelman A., Carlin J.B., Stern H.S., Rubin D.B. Bayesian data analysis. 2. New York: Chapman & Hall/CRC; 2004. [Google Scholar]
- Geman S., Geman D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1984;6:721–741. doi: 10.1109/TPAMI.1984.4767596. [DOI] [PubMed] [Google Scholar]
- Glas C.A.W., van der Linden W.J. Computerized adaptive testing with item cloning. Applied Psychological Measurement. 2003;23:249–263. [Google Scholar]
- Goldstein H. Multilevel statistical models. 3. London: Arnold; 2003. [Google Scholar]
- Harville D.A. Maximum likelihood approaches to variance component estimation and related problems. Journal of the American Statistical Association. 1977;72:320–338. doi: 10.2307/2286796. [DOI] [Google Scholar]
- Johnson, V.E., & Albert, J.H. (1999). Ordinal data modeling.
- Kass R.E., Raftery A.E. Bayes factors. Journal of the American Statistical Association. 1995;90:773–795. doi: 10.2307/2291091. [DOI] [Google Scholar]
- Kennedy M. Speed as a personality trait. Journal of Social Psychology. 1930;1:286–298. [Google Scholar]
- Laird N.M., Ware J.H. Random-effects models for longitudinal data. Biometrics. 1982;38:963–974. doi: 10.2307/2529876. [DOI] [PubMed] [Google Scholar]
- Lavine M., Schervish M.J. Bayes factors: What they are and what they are not. The American Statistician. 1999;53:119–122. doi: 10.2307/2685729. [DOI] [Google Scholar]
- Lee P.M. Bayesian statistics, an introduction. 3. New York: Arnold; 2004. [Google Scholar]
- Luce D.R. Response times: Their role in inferring elementary mental organization. New York: Oxford University Press; 1986. [Google Scholar]
- McCrea R.R., Costa P.T. Personality trait structure as a human universal. American Psychologist. 1997;52:509–516. doi: 10.1037/0003-066X.52.5.509. [DOI] [PubMed] [Google Scholar]
- McCulloch R.E., Rossi P.E. An exact likelihood analysis of the multinomial probit model. Journal of Econometrics. 1994;64:207–240. doi: 10.1016/0304-4076(94)90064-7. [DOI] [Google Scholar]
- McCulloch R.E., Polson N.G., Rossi P.E. A Bayesian analysis of the multinomial probit model with fully identified parameters. Journal of Econometrics. 2000;99:173–193. doi: 10.1016/S0304-4076(00)00034-8. [DOI] [Google Scholar]
- Mellenbergh G.J. A unidimensional latent trait model for continuous item responses. Multivariate Behavioral Research. 1994;29:223–236. doi: 10.1207/s15327906mbr2903_2. [DOI] [PubMed] [Google Scholar]
- Newton M.A., Raftery A.E. Approximate Bayesian inference with the weighted likelhood bootstrap. Journal of the Royal Statistical Society Series B. 1994;56:3–58. [Google Scholar]
- Patz R.J., Junker B.W. A straightforward approach to Markov chain Monte Carlo methods for item response models. Journal of Educational and Behavioral Statistics. 1999;24:146–178. [Google Scholar]
- Rabe-Hesketh S., Skrondal A. Parameterization of multivariate random effects models for categorical data. Biometrics. 2001;57:1256–1264. doi: 10.1111/j.0006-341X.2001.1256_1.x. [DOI] [PubMed] [Google Scholar]
- Reinsel G. Some results on multivariate autoregressive index models. Biometrika. 1983;70:145–156. doi: 10.1093/biomet/70.1.145. [DOI] [Google Scholar]
- Rost J. Rasch models in latent classes: An integration of two approaches to item analysis. Applied Psychological Measurement. 1990;14:271–282. doi: 10.1177/014662169001400305. [DOI] [Google Scholar]
- Schafer J.L., Yucel R.C. Computational strategies for multivariate linear mixed-effects models with missing values. Journal of Computational and Graphical Statistics. 2002;11:437–457. doi: 10.1198/106186002760180608. [DOI] [Google Scholar]
- Schnipke D.L., Scrams D.J. Modeling item response times with a two-state mixture model: A new method for measuring speededness. Journal of Educational Measurement. 1997;34:213–232. doi: 10.1111/j.1745-3984.1997.tb00516.x. [DOI] [Google Scholar]
- Schnipke D.L., Scrams D.J. Exploring issues of examinee behavior: Insights gained from response-time analyses. In: Mills C., Fremer M.P.J., Ward W., editors. Computer-based testing: Building the foundation for future assessments. Mahwah: Lawrence Erlbaum Associates; 2002. pp. 237–266. [Google Scholar]
- Schwarz G. Estimating the dimension of a model. The Annals of Statistics. 1978;6:461–464. doi: 10.1214/aos/1176344136. [DOI] [Google Scholar]
- Searle S.R., Casella G., McCulloch C.E. Variance components. New York: Wiley; 1992. [Google Scholar]
- Shah A., Laird N., Schoenfeld D. Random-effects model for multiple characteristics with possibly missing data. Journal of the American Statistical Association. 1997;92:775–779. doi: 10.2307/2965726. [DOI] [Google Scholar]
- Shi J.Q., Lee S.Y. Bayesian sampling based approach for factor analysis models with continuous and polytomous data. British Journal of Mathematical and Statistical Psychology. 1998;51:233–252. [Google Scholar]
- Sinharay S. Assessing fit of unidimensional item response theory models using a Bayesian approach. Journal of Educational Measurement. 2005;42:375–394. doi: 10.1111/j.1745-3984.2005.00021.x. [DOI] [Google Scholar]
- Sinharay S., Stern H.S. On the sensitivity of Bayes factors to the prior distributions. The American Statistician. 2002;56:196–201. doi: 10.1198/000313002137. [DOI] [Google Scholar]
- Sinharay S., Johnson M.S., Stern H.S. Posterior predictive assessment of item response theory models. Applied Psychological Measurement. 2006;30:298–321. doi: 10.1177/0146621605285517. [DOI] [Google Scholar]
- Snijders T.A.B., Bosker R.J. Multilevel analysis, an introduction to basic and advanced multilevel modeling. London: Sage Publishers; 1999. [Google Scholar]
- Spiegelhalter D.J., Best N.G., Carlin B.P., van der Linde A. Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society Series B. 2002;64:583–639. doi: 10.1111/1467-9868.00353. [DOI] [Google Scholar]
- Tate M.W. Individual differences in speed of response in mental test materials of varying degrees of difficulty. Educational and Psychological Measurement. 1948;8:353–374. doi: 10.1177/001316444800800307. [DOI] [PubMed] [Google Scholar]
- Thissen D. Timed testing: An approach using item response theory. In: Weiss D., editor. New horizons in testing: Latent trait test theory and computerized adaptive testing. New York: Academic Press; 1983. pp. 179–203. [Google Scholar]
- Vaida F., Blanchard S. Conditional Akaike information for mixed-effects models. Biometrika. 2005;92:351–370. doi: 10.1093/biomet/92.2.351. [DOI] [Google Scholar]
- van der Linden W.J. A lognormal model for response times on test items. Journal of Educational and Behavioural Statistics. 2006;31:181–204. doi: 10.3102/10769986031002181. [DOI] [Google Scholar]
- van der Linden W.J. Using response times for item selection in adaptive testing. Journal of Educational and Behavioral Statistics. 2007 [Google Scholar]
- van der Linden W.J. A hierarchical framework for modeling speed and accuracy on test items. Psychometrika. 2008;72:287–308. doi: 10.1007/s11336-006-1478-z. [DOI] [Google Scholar]
- van der Linden W.J., Guo F. Bayesian procedures for identifying aberrant response-time patterns in adaptive testing. Psychometrika. 2008 [Google Scholar]
- van der Linden W.J., Breithaupt K., Chuah S.C., Zang Y. Detecting differential speededness in multistage testing. Journal of Educational Measurement. 2007;44:117–130. doi: 10.1111/j.1745-3984.2007.00030.x. [DOI] [Google Scholar]
- Verdinelli I., Wasserman L. Computing Bayes factors using a generalization of the Savage–Dickey density ratio. Journal of the American Statistical Association. 1995;90:614–618. doi: 10.2307/2291073. [DOI] [Google Scholar]
- Verhelst N., Verstralen H., Jansen M. Models for time-limit tests. In: van der Linden W.J., Hambleton R.K., editors. Handbook of modern item response theory. New York: Springer; 1997. pp. 169–185. [Google Scholar]
- Wise S.L., Kong X.J. Response time effort: A new measure of examinee motivation in computer-based tests. Applied Measurement in Education. 2005;18:163–183. doi: 10.1207/s15324818ame1802_2. [DOI] [Google Scholar]
- Wise, S.L., Kong, X.J., & Pastor, D.A. (2007). Understanding correlates of rapid-guessing behavior in low-stakes testing: Implications for test development and measurement practice. Paper presented at the 2007 anual meeting of the National Council on Measurement in Education, Chicago, IL.