A new statistically-constrained deformable registration framework for MR brain images

Abstract

Statistical models of deformations (SMD) capture the variability of deformations from the template image onto a group of sample images and can be used to constrain the traditional deformable registration algorithms to improve their robustness and accuracy. This paper employs a wavelet-PCA-based SMD to constrain the traditional deformable registration based on the Bayesian framework. The template image is adaptively warped by an intermediate deformation field generated based on the SMD during the registration procedure, and the traditional deformable registration is performed to register the intermediate template image with the input subject image. Since the intermediate template image is much more similar to the subject image, and the deformation is relatively small and local, it is less likely to be stuck into undesired local minimum using the same deformable registration in this framework. Experiments show that the proposed statistically-constrained deformable registration framework is more robust and accurate than the conventional registration.

1 Introduction

Conventional deformable registration methods (Duncan and Ayache, 2000; Kamber et al., 1995; Rueckert et al., 1999; Shen and Davatzikos, 2002; Johnson and Christensen, 2002; Warfield et al., 2002; Toga and Thompson, 2001) aim to find a deformation field between two input images, called the template image and the subject image, by maximising the image-similarity-measure and simultaneously constraining/regularising the deformation field according to various deformable models, e.g., smooth and continuous regulations, Spline models, etc. When the training samples, i.e., the deformation fields from the template images to a number of subject images, are available, statistical models that capture the variability of these deformation fields can be utilised to constrain the registration procedure in order to obtain more robust registration results (Twining et al., 2005). Nevertheless, a good statistical model must effectively limit the searching space of deformations and, at the same time, accurately capture complex nature of deformation fields.

The popular principal component analysis (PCA)-based algorithms (Cootes et al., 1994, 1995; Miller et al., 1997) can be used to capture the variability of shapes using the principal modes of shape variation. However, they can only be applied to relatively low dimensional data, such as object contours and they often fail when applied to deformation fields, due to under-training in practical settings, e.g., high dimensionality and small training samples. Different statistical algorithms have been proposed to deal with these problems, among which the wavelet-PCA model (Coifman and Wickerhauser, 1992; Xue et al., 2006b), applying PCA model in each wavelet band of deformation fields has been approved to be more accurate and effective for estimating pdfs of deformations. To alleviate possible discontinuity or some negative Jacobians that could be generated by the wavelet-PCA model, the statistical models of deformations (SMD) (Xue et al., 2006b) is presented to use additional Jacobian determinant regularisation to guarantee correct topology of the smooth deformation field. In this work, we used the wavelet-PCA model coupled with a simplified Jacobian determinants regularisation to model the SMD, which is not only effective to capture the statistics of deformations but also more efficient in calculation.

After training the SMD, we need to design a method about how to constrain a deformable registration algorithm using this SMD. In this paper, we propose a statistically-constrained deformable registration using the Bayesian framework formulation. The basic idea of this framework is to adaptively deform the template image according to the statistics of deformations and generate an intermediately deformed template image, which is much more similar with the input subject image and then register the input subject image with the deformed template image by using a conventional deformable registration algorithm. This procedure can be iteratively performed until convergence. Since the intermediately deformed template image is more similar to the input subject image than the original template image, the registration between them is much easier, due to relatively small and local deformations between these two images, i.e., it is less likely to be stuck into local minimum. Thus, comparing to the conventional method, more robust and accurate registration results can be obtained by using the new framework.

In experiments, we evaluated the performance of the proposed registration framework by incorporating the proposed method with the HAMMER registration algorithm (Shen and Davazikos, 2002), referred to as statistically-constrained HAMMER or cHAMMER, i.e., we compared the performance of cHAMMER and HAMMER using simulated images. The experimental results show that the statistically-constrained deformable registration framework provides more robust and accurate registration results. Notice that this statistical registration framework can be applied to other conventional image registration algorithms.

The rest of this paper is organised as follows. Section 2 presents the methods, including the SMD and the statistically-constrained deformable registration framework. Section 3 presents the comparative results and Section 4 gives the conclusion of this study.

2 Method

In this section, we first briefly introduce the wavelet-PCA based SMD used to capture the statistics of deformation fields from the template space to the subject image space (Xue et al., 2006b). Then, the statistically-constrained deformable registration framework is proposed in detail.

2.1 Statistical model of deformations

Since the deformation fields of 3-D volumetric images can have thousands or more degrees of freedom, the conventional PCA-based statistical model are limited to capture the full range of anatomical variability and it is a challenging task to capture the variability of the high-dimensional fields using relatively small number of training samples, e.g., one or two hundreds of images. In this paper, we employ the wavelet-PCA statistical model of deformation (Xue et al., 2006b) and use this SMD to constrain the traditional deformable registration based on a Bayesian framework. The wavelet-PCA SMD method is briefly introduced in this section.

Denoting f(x), x ∈ Ω_t, as the deformation field defined over the template image domain Ω_t, the goal of SMD is to estimate the pdf of f, i.e., p(f), from a relatively small number of training samples. In order to capture finer and more localised variations of f, SMD follows and extends the wavelet-based PCA model (Xue et al., 2006b). The wavelet-PCA model decomposes f using the wavelet packet transform (WPT) (Mallat, 1998) and subsequently captures within-scale statistics via PCA in each wavelet band. The fundamental assumption in wavelet-PCA is that the wavelet-based rotation renders the covariance matrix of deformation f close to block-diagonal, thereby enabling a more accurate estimation of the statistical distribution in each block (wavelet band) from a limited set of examples, compared to the usual sample covariance estimation, due to both of lower dimensionality and relatively strong correlations among variables.

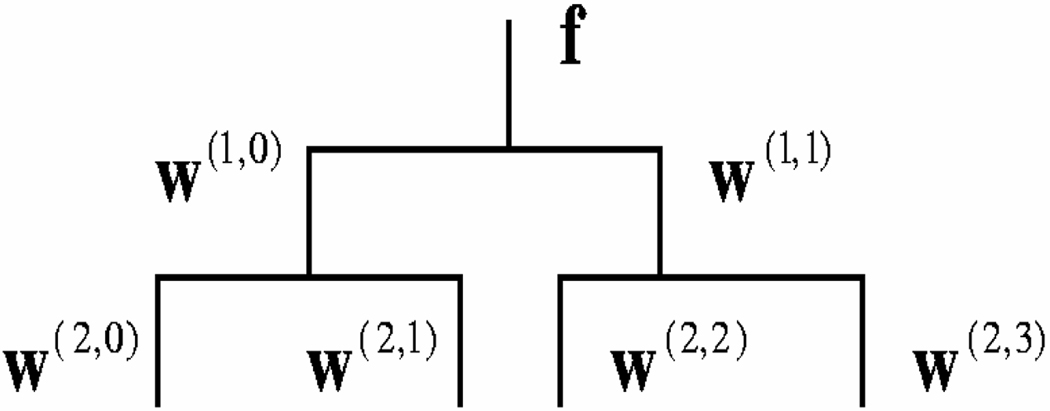
The wavelet-PCA model is used to estimate the pdf of deformation fields, i.e., p(f), using N samples. It first applies an L-level WPT to each sample f and then constructs a PCA model of the wavelet coefficients of each wavelet band at level L and finally it combines the pdfs of different wavelet bands together. Figure 1 illustrates the structure of two-level one-dimensional WPT. For 3-D WPT, the wavelet coefficients at level l are represented by w^(l,b), b = 0, 1, …, Bl − 1, where l represents the WPT level and b indicates the band number. B_l = 8^l and l = 1, 2, …, L. At each level, the first wavelet coefficient w^(l,0) always represents the low-pass wavelet coefficients and the rest are the high-pass wavelet coefficients. Thus, the deformation f is also referred to as w^(0,0).

Figure 1.

The tree-structure of a two-level WPT of one-dimensional data

After performing the L-level WPT, f can be represented by all the wavelet coefficients at level L, i.e., w^(L,b), b = 0, 1, …, B_L − 1. Assuming that all the different bands at resolution L in the wavelet subspaces are independent, the wavelet-PCA estimates the pdf of f as,

$$p(\mathbf{f})={\displaystyle \prod _{b=0}^{B_{L-1}}p({\mathbf{w}}^{(L,b)}).}$$ (1)

The pdf of each band (L, b), p(w^(L,b)), can be estimated by applying PCA to all the wavelet coefficients of N deformation field samples of that wavelet band, denoted as w^(L,b), where s represents the index of each sample and s = 1, 2, …, N. After performing PCA, we obtain the mean of the wavelet coefficients w̄^(L,b) and the matrix Φ^(L,b) formed by the K_(L,b) eigenvectors of the covariance matrix of these wavelet coefficients corresponding to the K_(L,b) largest eigenvalues ${\lambda }_j^{(L,b)}$, j = 1, …, K_(L,b), of that covariance matrix. Therefore, w^(L,b) can be represented by its projected vector or feature vector v_(L,b) in the space spanned by the K_(L,b) principal components as,

$${\mathbf{v}}^{(L,b)}={\Phi }^{{(L,b)}^T}({\mathbf{w}}^{(L,b)}-{\overline{\mathbf{w}}}^{(L,b)}).$$ (2)

Then, the pdf of f in equation (1) is represented by,

$$p(\mathbf{f})={\displaystyle \prod _{b=0}^{B_{L-1}}}\left\{c_{(L,b)}\text{exp}\left[-{\displaystyle \sum _{j=1}^{K_{(L,b)}}\frac{v_j^{{(L,b)}^2}}{2{\lambda }_j^{(L,b)}}}\right]\right\}$$ (3)

where c_(L,b) is the normalisation coefficient and $v_j^{(L,b)}$ is the jth element of feature vector v^(L,b).

We stress the importance of using PCA within each wavelet band, which is in agree with the commonly used independence assumption for wavelet coefficients. In particular, PCA is known to be the optimal linear expansion, provided that a good estimate of the covariance matrix is available. Although sample covariance is a very inaccurate estimate of the covariance of f, the sample covariance at various scales provides a much better estimate of the covariance at that scale, because of the relatively low dimensionality of each wavelet band. As a result, the wavelet-PCA model can capture correlations between adjacent spatial locations at a given scale.

Ideally, if the wavelet-PCA model captures the statistics of deformation f accurately, we can just use it as the statistical model; however, the assumption that the covariance matrix of f is block-diagonal in the wavelet packet basis does not hold exactly. Although it is well-known that for broad classes of signals, correlations across scales diminish rapidly, they are nonetheless non-negligible for adjacent scales. In order to alleviate this problem, we observe that additional constraints imposed on the deformation fields can be used to define subspaces in which the deformation must belong to. Therefore, SMD requires that a valid deformation field also satisfy the positive Jacobian determinant and smoothness regularisation. This can be easily achieved by performing a Jacobian determinant regularisation with smoothness constraints (Karacali and Davatzikos, 2004).

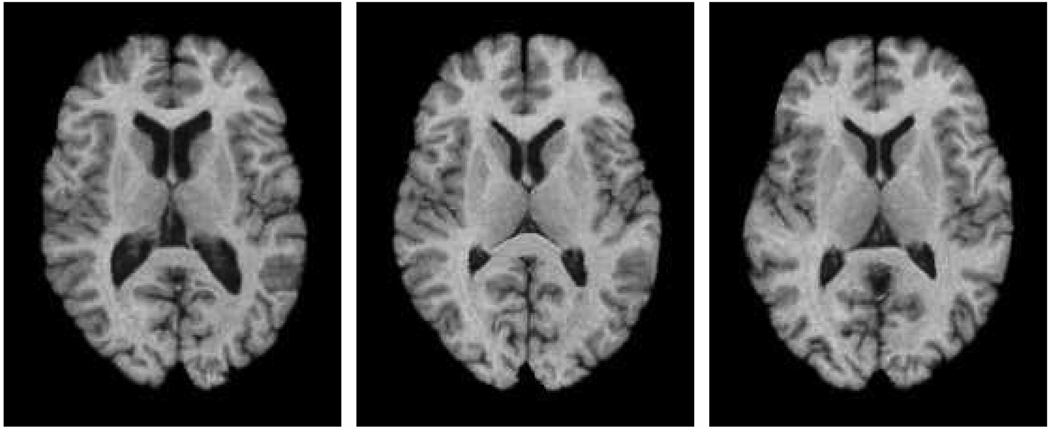
The proposed SMD can be used to simulate new MR brain images by randomly sampling the wavelet-PCA space [so that the randomly generated feature vectors satisfy equation (4) described below] and then perform inverse WPT transforms and then perform a Jacobian determinant regularisation. Figure 2 shows three such randomly generated images, using a SMD model trained from 158 sample deformations obtained by applying HAMMER registration. It can be seen that various MR brain images with different shapes can be simulated. The proposed SMD has been approved to be more accurate in capturing the statistics of deformation fields than the conventional PCA-based method and been used for simulating realistic images for evaluation of atlas-based registration and segmentation algorithms (Xue et al., 2006b).

Figure 2.

Example of the randomly simulated images using the statistical model of deformation

The SMD can also be used to regularise an input deformation field based on the statistics learned from training samples. Given an input deformation field, we can project it onto the space of the wavelet-PCA space and then regularise its Jacobian determinants. Such a procedure is referred to as the ‘SMD regularisation algorithm’ and it consists of the following three steps:

• Step 1
  Project the input deformation field onto the wavelet-PCA model and constrain their feature vectors so that they are located within the range of valid deformation fields determined by the eigenvalues,

  $${\displaystyle \sum _{j=1}^{K_{(L,b)}}\frac{v_j^{{(L,b)}^2}}{2{\lambda }_j^{(L,b)}}}<\delta {}_{(L,b)},b=0,1,\dots ,B_L,$$ (4)

  where δ_(L,b) is the threshold for band (L,b) and we denote the constrained feature vectors as v′^(L,b)
• Step 2
  Reconstruct the wavelet coefficients using the constrained feature vectors,

  $${{\mathbf{w}}^{\prime }}^{(L,b)}={\Phi }^{(L,b)}{{\mathbf{v}}^{\prime }}^{(L,b)}+{\overline{\mathbf{w}}}^{(L,b)},$$ (5)

  and perform inverse WPT transforms to generate the new projected deformation field.
• Step 3Perform Jacobian determinant regularisation algorithm (Karacali and Davatzikos, 2004) on the deformation field, so that it is smooth and has valid topology.

2.2 Statistically-constrained deformable registration – a Bayesian framework

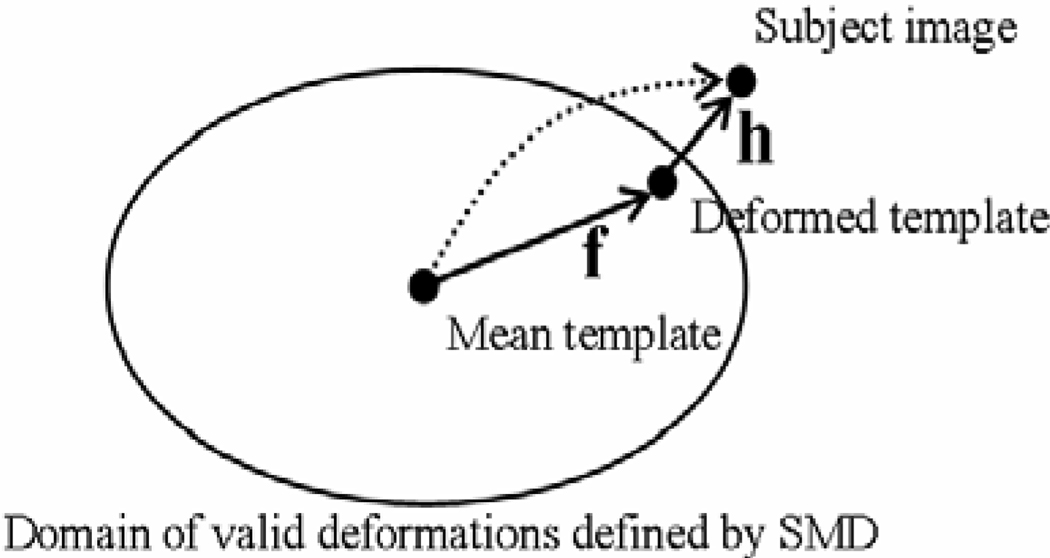
After estimating the statistical model of deformation fields, we can use it to constrain a deformable registration. Let T and S be the template and the subject images, the deformed template image can be denoted as T (f(x)), where f is the deformation of the template image. Let h be the deformation between the deformed template T (f ()) and the subject image S, the statistically-constrained deformable registration estimates both h and f (see Figure 3), according to the Bayesian framework, i.e., h and f can be obtained by maximising their joint posterior distribution, p(h, f|S, T),

$$p(\mathbf{h},\mathbf{f}|S,T)=\frac{p(\mathbf{h})p(S,T|\mathbf{f})p(\mathbf{h}|\mathbf{f},S,T)}{p(S,T)}$$ (6)

where p(f) is the prior distribution of deformation fields and p(S, T|f) is the likelihood of the images for a given deformation f, thus to maximise p(f)p(S, T|f) we need to find an f according to its prior distribution, which also aligns the template and the subject images well. p(h|f, S, T) is the conditional likelihood of h. To maximise this likelihood, we need to find a deformation h, which registers the deformed template and the subject images accurately. These two tasks are accomplished by the respective two steps described below. Figure 3 illustrates the relationship between the template and the subject images, as well as h and f. For simplicity, the template image shown in Figure 3 is the one generated using the mean deformation.

Figure 3.

Instead of directly registering the template image with the subject image (illustrated by the dotted line), in this work, the template image is first warped toward the subject image in the space of SMD (by deformation f) and a conventional registration is then performed for the deformed template and the subject images (using deformation h)

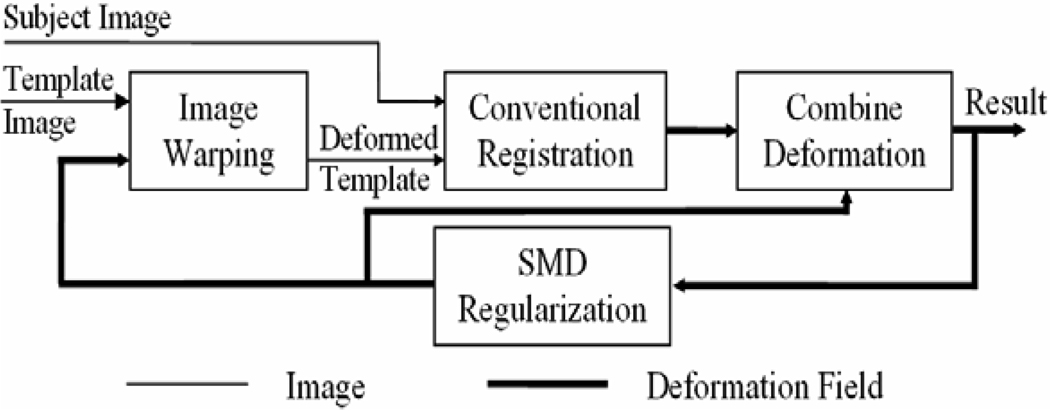
The algorithm is implemented using the following two iterative steps (see the structure in Figure 4):

• Step 1Use the SMD regularisation algorithm to regularise the combined deformation h(f) and generate a new deformation f and a new deformed template image T(f).
• Step 2Apply a conventional registration algorithm to register the deformed image T(f) with the subject image S and generate a new deformation h.

Figure 4.

The structure of the statistically-constrained deformable registration

The initial deformation between the template image and the subject image can be obtained by using the traditional registration and this iterative procedure usually converges after 2 5 iterations.

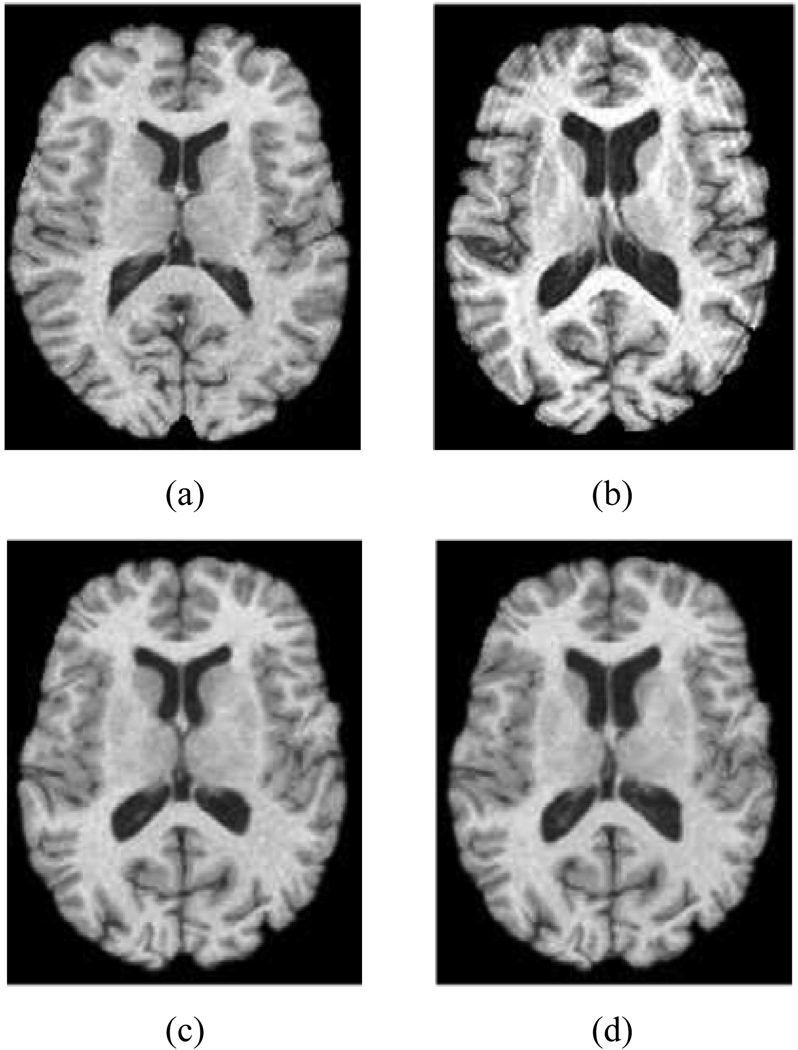
Figure 5 gives an example of the statistically-constrained deformable registration. It can be seen that compared to the original template image in Figure 5(a), the intermediate deformed template image in Figure 5(c) is more similar to the subject image in Figure 5(b), which renders the registration between Figure 5(b) and Figure 5(c) relatively easy than that between Figure 5(a) and Figure 5(b), e.g., the deformation between them is relatively small and local.

Figure 5.

An example of the registration results, (a) the template image (b) the subject image (c) the intermediate deformed template image (d) final registration result: the warped template image

In all the experiments, we have used the HAMMER registration algorithm in our framework to register images T(f) and S, referred to as cHAMMER. Notice that the deformation in this paper consists of two parts, one is a deformation of the template image defined according to SMD and the other is a non-linear deformation by registering the warped template with the subject image using a conventional registration; whereas in our previous work (Xue et al., 2006a), we only used the statistical model of the deformations as a regularisation and thus the regularised registration result is regarded as the final results. It is in this context that the statistically-constrained deformable registration framework presented in this paper can improve not only the robustness but also the accuracy for deformable registration. Moreover, many traditional registration algorithms that take two input images as well as an initial deformation between them can be incorporated in this new framework.

3 Results

Since for real MR brain images, there are no ground truth about the deformation from one image onto another. In order to evaluate the performance of the proposed algorithm, in this paper, we first apply our algorithm to register simulated images where the deformations are known and compared the registration errors between the traditional HAMMER algorithm and its statistically-constrained version, cHAMMER. Moreover, we also simulated atrophy for a group of real data and thus we have two groups of images with known group differences. We then used HAMMER and cHAMMER to register these two groups of the data onto a standard template image and analysed the group differences. Clearly, a robust registration will produce more stable registration and thus make the two groups of images more distinctive.

3.1 Comparison of accuracy of registration using simulated deformations and images

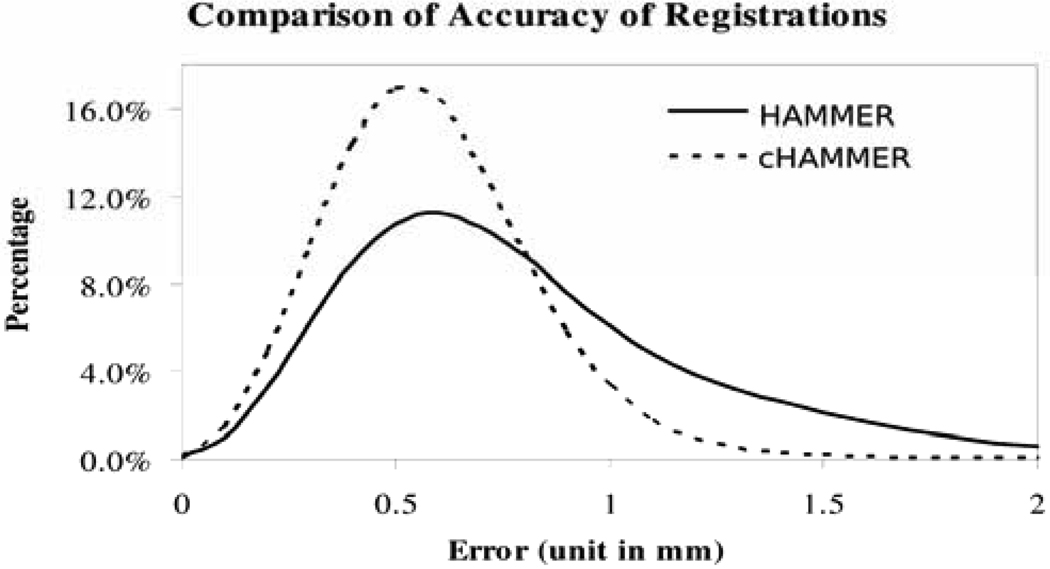
Simulated deformations and images are used to compare the registration accuracy of HAMMER and cHAMMER. First, we used two groups of T1-weighted MR brain images as the training samples and then trained two SMD separately, where the HAMMER registration algorithm was used to registering the images and to generate the training samples. The reason to use two groups of data is that the training images used for simulating images and for constraining the deformable registration are separated. After training the two SMDs, one was used for simulating new deformations and images and another was used for constraining the deformable registration algorithm. We simulated nine such images and registered them onto the template image space using HAMMER and cHAMMER, respectively and then calculated the deformation errors between the registration results and the simulated ground truth. The histogram of these voxel-wise deformation errors of all the nine images are shown in Figure 6. It can be seen that cHAMMER yields more accurate registration than HAMMER, with respective population means as 0.59 mm and 0.86 mm. Therefore, using the proposed statistically-constrained deformable registration framework, the accuracy of a traditional image registration can be improved.

Figure 6.

Comparison of accuracy of registrations

3.2 Comparison of robustness of registration for group analysis

The second experiment focuses on applying the registration algorithms for group analysis. For the same group of data, after registering them onto the standard template space, we apply the traditional statistical parametric mapping (SPM) software (Statistical Parametric Mapping) and perform a paired t-test of the two groups of image data. Obviously, different registration algorithms will yield different group analysis results, but the one that generates more robust and accurate registration results for two groups of images with known differences performs better.

In this experiment, from a group of normal MR brain images (ten images); we simulated atrophy on the superior temporal gyrus and the precentral gyrus and then registered all these images onto the template image. Using the tissue density maps calculated from the Jacobian determinants of the resultant deformation fields for different tissues gray matter (GM), white matter (WM) and ventricular CSF (VN), we performed a paired t-test for group analysis using the SPM software package. A smaller p-value or a larger t-value of this t-test indicates better separation. Table 1 shows the statistical measures for the two clusters detected in the locations of the precentral gyrus and the superior temporal gyrus, respectively. It can be seen that smaller p-values (both of p_FWE–corr and p_FDR–corr ) and larger t-values are obtained by cHAMMER. Thus, according to these experiments, cHAMMER generated more robust and stable deformation fields and is more powerful in detecting group differences.

Table 1.

Paired t-test for the two image groups

Cluster	HAMMER	cHAMMER
Cluster 1	pFWE–corr = 0.017	pFWE–corr = 0.003
precentral	pFDR–corr = 0.02	pFDR–corr = 0.003
gyrus	T = 17.44	T = 21.58
Cluster 2	pFWE–corr = 0.19	pFWE–corr = 0.043
sup-temp	pFDR–corr = 0.02	pFDR–corr = 0.006
gyrus	T = 12.79	T = 15.50

4 Conclusions

This paper proposed a statistically-constrained deformable registration framework. During the registration, the template image can be adaptively warped according to the SMD and the conventional registration is performed by aligning the input subject image with the intermediately deformed template image. Because of the use of statistical model constraints and because the intermediate template is much more similar to the subject image, more robust and accurate registration is achieved compared to the conventional registration. The proposed framework can be easily applied to other conventional deformable registration methods.

Biographies

Zhong Xue is the Director of Medical Image Analysis Lab, in The Center for Biotechnology and Informatics of The Methodist Hospital Research Institute, and a faculty with Weill Medical College of Cornell University. Before joining TMHRI, he had worked in both academia medicine and industry, including University of Pennsylvania, Panasonic, and Abla-Tx Inc. He is an IEEE Senior Member. His research interests include medical image computing, multimodality image registration and navigation, software and algorithms for image guided diagnosis and therapy.

Dinggang Shen is an Associate Professor in the Department of Radiology and BRIC at UNC-Chapel Hill. Before joining UNC, he was an Assistant Professor in the University of Pennsylvania from 2002 to 2008, and a faculty member in Johns Hopkins University in 2001 and 2002. He is on the Editorial Board of Pattern Recognition, International Journal for Computation Vision and Biomechanics, and International Journal of Image and Graphics. He has published over 200 articles in journals and proceedings of international conferences. He is a Senior Member of IEEE.