Table 1.
Summary of Notation.
| c | index of spike trains c = 1, 2, …, C |
| m | index of simulated Markov chains m = 1, 2, …, M |
| t | continuous-time index t ∈ [0, T] |
| ti | spike timing of the ith spike in continuous time |
| Δ | smallest time bin size |
| k | discrete-time index k = 1, 2, …, K, KΔ = T |
| yk | number of counts observed from discrete-time Markov chain, yk ∈ {0, ℕ} |
| Sk | discrete-time first-order Markov state, Sk ∈ {1, …, L} |
| S0 | initial Markov state at time 0 |
| S0:T, S1:k | history of the Markov state from time 0 to T (or 1 to k) |
| n | number of state jumps within the latent process S0:T |
| l | index of state jumps l = 1, 2, …, n |
| {S(t); 0 ≤ t ≤ T} | realization of hidden Markov process |
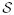 = (n, τ, χ) = (n, τ, χ) |
triplet that contains all information of continuous-time Markov chain {S(t)} |
| τ = (τ0, …, τn) | (n + 1)-length vector of the sojourn times of {S(t)} |
| χ = (χ0, …, χn) | (n + 1)-length vector of visited states in the sojourn times of {S(t)} |
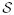 (0) (0)
|
initial state of MCMC sampler |
| νl | ν0 = 0, |
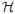 0:T, 0:T, 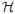 1:K 1:K
|
history of point-process observations from time 0 to T (or 1 to k) |
| N(t), Nk | counting process in continuous and discrete time, N(t), Nk ∈ {0, ℕ} |
| dN(t), dNk | indicator of point-process observations, 0 or 1 |
| Pij | transition probability from state i to j for a discrete-time Markov chain, Σj Pij = 1 |
| qij | transition rate from state i to j for a continuous-time Markov chain, Σj qij = 0 |
| ri = qii | total transition rate of state i for a continuous-time Markov chain, ri = Σj≠i qij |
| πi | initial prior probability Pr(S0 = i) |
| ak(i) | forward message of state i at time k |
| bk(i) | backward message of state i at time k |
| γk(i) | marginal conditional probability Pr(Sk = i ∣ 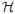 0:T) 0:T) |
| ξk(i, j) | joint conditional probability Pr(Sk−1 = i, Sk = j ∣ 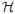 0:T) 0:T) |
| log likelihood of the complete data | |
R(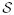 → → 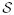 ′) ′) |
proposal transition density from state 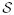 to to 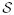 ′ ′ |
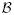 = = 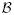 1 1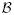 2 2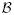 3 3
|
prior ratio × likelihood ratio × proposal probability ratio |
acceptance probability, 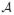 = min(1, = min(1, 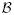 ) ) |
|
| Jacobian | |
| λk | conditional intensity function of the point process at time k |
| θ | parameter vector that contains all unknown parameters |
| p(x) | probability density function |
| F(x) | cumulative distribution function, |
| Φ(x) | gaussian cumulative distribution function |
| erf(x) | error function |
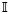 (·) (·) |
indicator function |
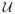 (a, b) (a, b) |
uniform distribution within the region (a, b) |
