Multivariate Data Analysis as a Semi-quantitative Tool for Interpretive Evaluation of Comparability or Equivalence of Aerodynamic Particle Size Distribution Profiles

Abstract

The purpose of this article is to investigate the performance of multivariate data analysis, especially orthogonal partial least square (OPLS) analysis, as a semi-quantitative tool to evaluate the comparability or equivalence of aerodynamic particle size distribution (APSD) profiles of orally inhaled and nasal drug products (OINDP). Monte Carlo simulation was employed to reconstitute APSD profiles based on 55 realistic scenarios proposed by the Product Quality Research Institute (PQRI) working group. OPLS analyses with different data pretreatment methods were performed on each of the reconstituted profiles. Compared to unit-variance scaling, equivalence determined based on OPLS analysis with Pareto scaling was shown to be more consistent with the working group assessment. Chi-square statistics was employed to compare the performance of OPLS analysis (Pareto scaling) with that of the combination test (i.e., chi-square ratio statistics and population bioequivalence test for impactor-sized mass) in terms of achieving greater consistency with the working group evaluation. A p value of 0.036 suggested that OPLS analysis with Pareto scaling may be more predictive than the combination test with respect to consistency. Furthermore, OPLS analysis may also be employed to analyze part of the APSD profiles that contribute to the calculation of the mass median aerodynamic diameter. Our results show that OPLS analysis performed on partial deposition sites do not interfere with the performance on all deposition sites.

INTRODUCTION

It is generally believed that aerosol particles greater than 10 µm in aerodynamic diameter deposit primarily in the head and are swallowed subsequently rather than reaching the lungs (1). Lung delivery requires particle size in the range of 1–5 µm (2–4), which deposit either centrally or peripherally in the lungs depending on particle size. Therefore, aerodynamic particle size distribution (APSD) is an important in vitro characteristic of orally inhaled and nasal drug product (OINDP) because of a plausible link between particle size and eventual deposition in the respiratory tract. The interest to develop a statistical method to determine in vitro bioequivalence came from the practical need from both the regulators and the drug manufacturer. Once innovator companies make changes to a drug product or drug manufacturers plan to develop a generic version of a drug product, evidence should be provided to the regulators that the new or modified product has an APSD profiles sufficiently similar to that of the original product.

The chi-square ratio statistic (5) proposed in the 1999 US FDA guidance (6,7) was developed using Anderson eight-stage cascade impactor (8) applied to albuterol metered-dose inhaler data. In order to study this test’s applicability to a broad range of OINDP profiles, a working group involving scientists from industry, academia, FDA, and US pharmacopeia was established through the Product Quality Research Institute (PQRI; 9). The working group expended a great effort in investigating this chi-square ratio statistics. The work began with developing a simulation method capable of modeling APSD profiles and translating the chi-square ratio statistics proposed by the FDA into an executable algorithm (10). The working group first studied the stability of the chi-square ratio test on pairs of identical profiles, which showed that the stability increased as the number of stages increases and less stable for profiles that are common to metered-dose inhalers (MDIs) and dry powder inhalers (DPIs) (11). The next study focused on pairs of profiles differing in a specified and systematic way on a single deposition site, which gave rise to a total number of 38 scenarios (11,12). The findings from this study led the working group supplementing the chi-square ratio statistics with a population bioequivalence (PBE) test based on impactor-sized mass (ISM; 13) in order to increase the discriminating ability of the overall statistical procedure (14). Based on the study of this combination test (i.e., chi-square ratio test and ISM-PBE test), the working group produced a final report in 2007 on a statistical procedure for determining equivalence (14). Due to the deficiencies of the combination test, no recommendations were made by the working group for APSD profiles comparison.

In this article, we proposed another method to evaluate the comparability or equivalence of APSD profiles. The new method is based on multivariate data analysis, especially orthogonal partial least square (OPLS) analysis. Multivariate data analysis can be generally divided into two categories (15). One is the unsupervised method such as principal component analysis. The other one is the supervised method such as partial least square (PLS) analysis and orthogonal partial least square analysis. Principal component analysis is different from orthogonal partial least square analysis in that a priori knowledge of the identity of the profiles was not employed when patterns are assessed (15). Principal component analysis is generally employed as a pattern recognition tool before proceeding to the supervised method such as OPLS. Orthogonal partial least square analysis relates a matrix containing independent variables such as mass deposition on each deposition site to a matrix containing dependent variables such as profile membership in this case. OPLS analysis is frequently employed as a discriminant analysis to retrieve information lying in independent variables that may result in class separation. However, the main objective of this paper is not to use OPLS analysis to dissect out the independent variables contributing to class separation. Rather, the capability to detect difference between test and reference profiles revealed by OPLS model fitting is our primary goal. There are three reasons for proposing this method: (1) an APSD profile contains information from multiple deposition sites and therefore is a multivariate measurement (1); (2) mass deposition on each stage is not independent from each other. It has been suggested that the deposition on different stages may co-vary between each other (1) and this was indeed considered in the Monte Carlo simulation of 55 realistic scenarios provided by the working group (16,17); (3) principal components calculated in the OPLS analysis are all orthogonal and thus can resolve the issue of covariance (15). We began our work with first reconstituting 55 realistic scenarios by Monte Carlo simulation. Profiles generated were subjected to OPLS analysis to derive a parameter Eq as described in the methods. Finally, we compared the performance of the OPLS analysis with that of the combination test in terms of achieving greater consistency with the working group evaluation.

METHODS

Monte Carlo Simulation

Monte Carlo simulation was performed in ADAPT II (University of Southern California) to reconstitute 55 APSD profiles provided by the PQRI working group (14,16,17). Information about the mean and standard deviation for mass deposition on each site were readily available from the profiles provided. They were used as parameters for Monte Carlo simulation in ADAPT II. Population simulation with output noise assuming normal distribution of mass deposition on each stage was adopted. Monte Carlo simulations with a number of 5,000 were performed and repeated three times for each of the 55 realistic scenarios. The averages were taken for each scenario. In some cases, simulations with different numbers were performed for the purpose of demonstration. Data generated were organized in Microsoft® Excel for each scenario.

Multivariate Data Analysis

OPLS analysis was carried out in SIMCA-P 11.5 (Umetrics) and was employed to compare test profiles with reference profiles in all scenarios. Mass deposition data (X variables) were pretreated with either Pareto scaling or unit-variance scaling in addition to mean centering. Reference and test profiles are coded as 0 and 1 (Y variables) respectively. In order to normalize mass deposition, absolute mass data were first normalized to percent mass deposition data in Excel before proceeding to OPLS analysis. The first two principal components are calculated in all cases for the convenience of plotting. However, the R² for OPLS model fitting based on the first principal component was recorded. Eq was defined as equal to 1 − R² and served as a measure of equivalence between test and reference profiles for all 55 scenarios.

Chi-square Test

Chi-square test was carried out in Minitab 14.1 (Minitab Inc.) to compare OPLS analysis (with Pareto scaling) with combination test proposed by the Food and Drug Administration (FDA) and the PQRI working group. The difference (Δ) between the working group evaluation and Eq (by OPLS analysis) or proportion (by the combination test) was divided into three categories: Δ≥0.5, 0.3≤Δ<0.5 and Δ<0.3. A p value less than 0.05 was considered as statistically significant.

RESULTS AND DISCUSSION

Monte Carlo Simulation of 55 Realistic Scenarios

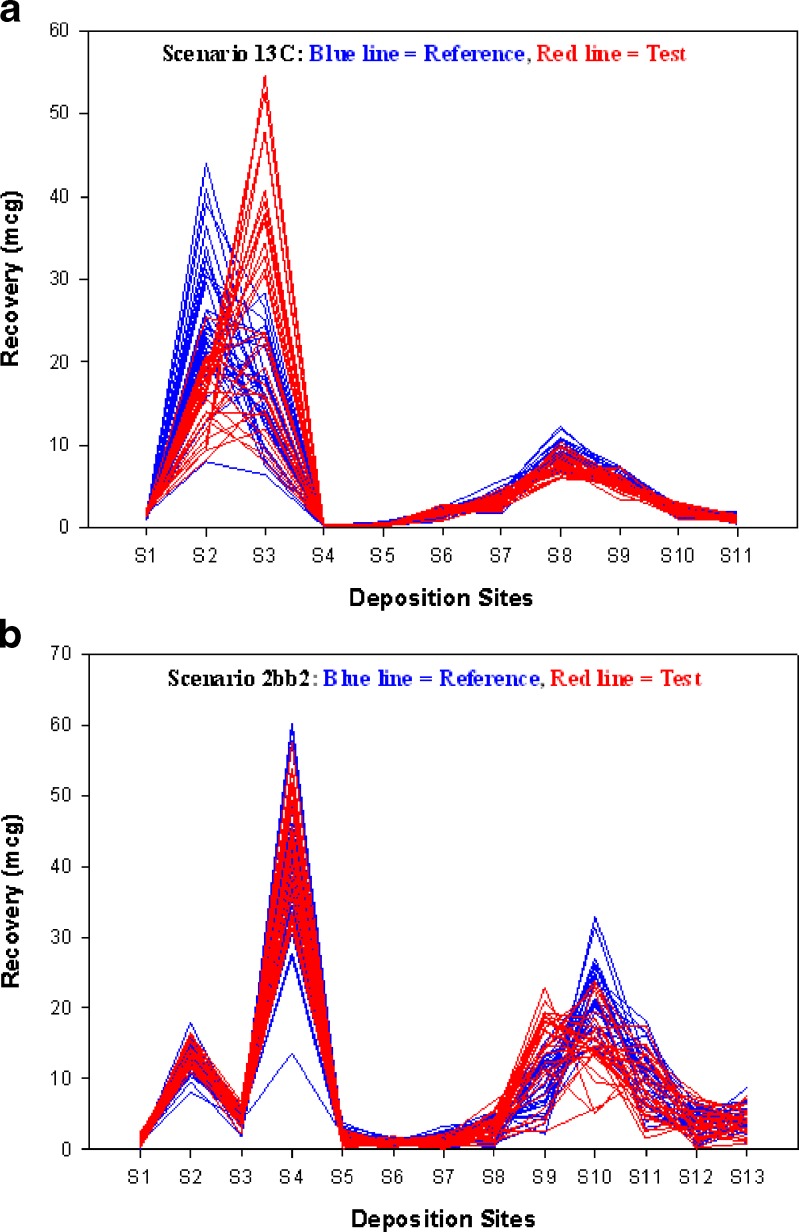
All 55 realistic scenarios have been simulated by Monte Carlo simulation. Among these profiles, only two scenarios were chosen to represent significant variability in the upper deposition sites between test and reference profiles in scenario 13c (Fig. 1a) as apposed to in the lower deposition sites in scenario 2bb2 (Fig. 1b). Profiles simulated here are slightly different in appearance from those provided by the PQRI working group (14,16,17). This is possibly due to the inherent variability of Monte Carlo simulation. A simulation number of 30 was chosen for both scenarios.

Fig. 1.

Reconstituted aerodynamic particle size distribution profiles for scenario 13c and scenario 2bb2 (Monte Carlo simulations with a number of 30 were generated for each reference and test profiles). a. Scenario 13c. b. Scenario 2bb2

Comparison of Chi-square Ratio Statistics and Orthogonal Partial Least Square Analysis with Respect to Profile Comparison

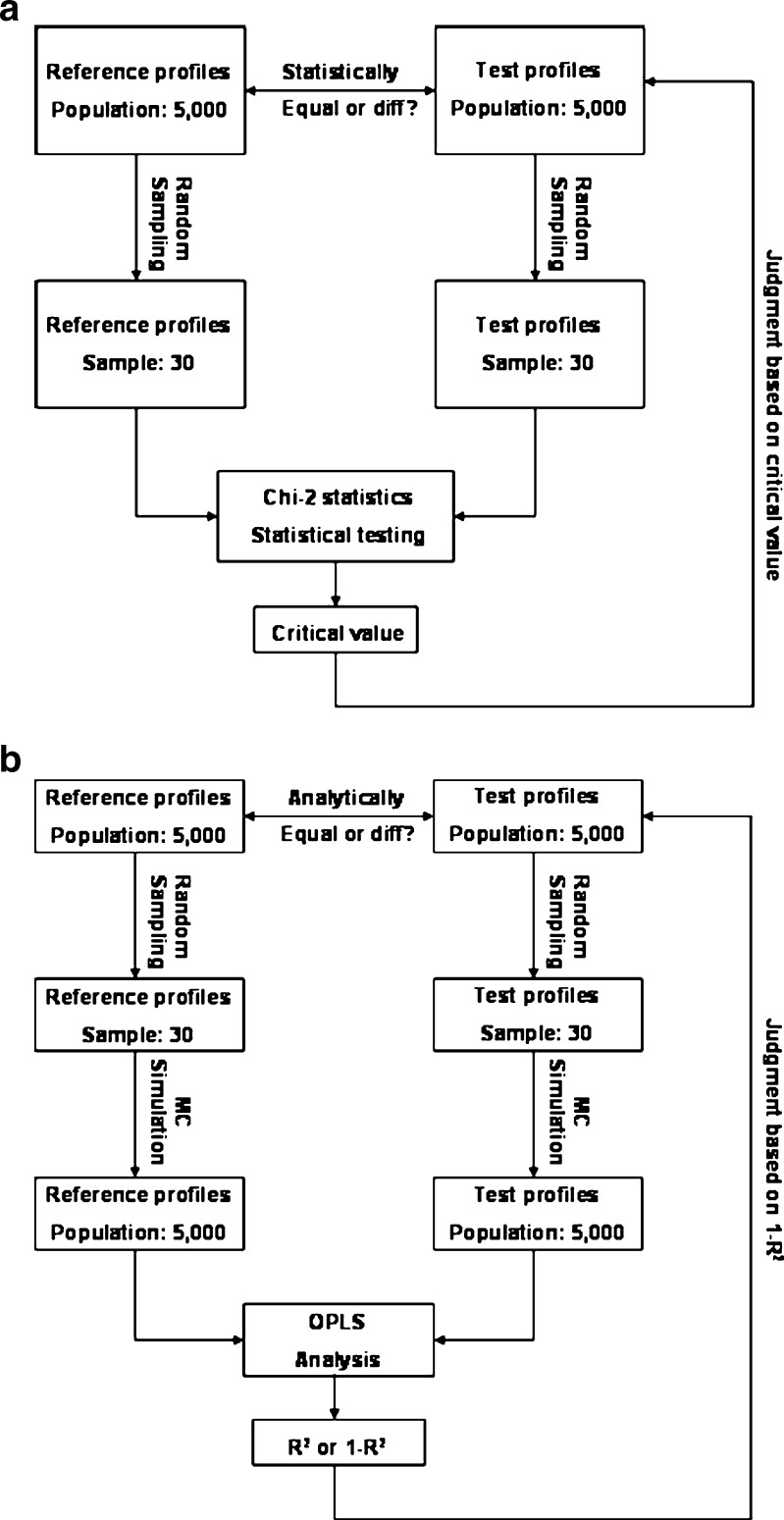
It was suggested that 30 reference and test inhalers should be sampled individually and subject to chi-square ratio statistics (1,11,14). A sample size of 30 was considered necessary to represent the random sampling of a population of dry powder inhalers or metered-dose inhalers manufactured. In addition, this is also a practical number, which requires a considerable yet manageable amount of sampling work. Figure 2a shows the flowchart of the chi-square ratio statistics. Thirty reference and test inhalers are randomly sampled from corresponding populations (e.g., 5,000). Sample profiles for these 30 inhalers are collected and then subject to chi-square ratio statistics. In an attempt to set up an appropriate critical value for chi-square ratio statistics, such statistical testing based on 30 samples is repeated hundreds of thousands of times to obtain a distribution of statistics, upon which a reasonable critical value may be chosen. It should be noted that the statistics obtained based on a sample size of 30 actually gives the possibility of equivalence between test and reference profiles from two corresponding populations rather than two samples. In contrast to chi-square ratio statistics, Fig. 2b shows the rationale for OPLS analysis as an analytical tool to judge equivalence between two populations. First, it should be emphasized that the method developed based on OPLS analysis is an analytical tool rather than a statistical test. There is no p value associated with this method. R² or its derivative Eq was instead used as an indicator of equivalence between test and reference profiles (see explanation in the following section). This method also begins with a random sampling of 30 samples consistent with the chi-square ratio statistics. The sample mean and standard deviation of mass at each deposition site was calculated based on impactor data from these 30 samples. Rather than statistical testing, the sample mean and standard deviation was used for Monte Carlo simulation to obtain simulated population profiles. Ideally, the population mean and standard deviation of mass deposition should be used for the population simulation. However, these numbers will not be known until all the inhalers are characterized, which are not practical. Therefore, we consider a sample size of 30 as both necessary and practical since the more samples collected the more accurately sample mean and standard deviation can represent population mean and standard deviation. The size for population simulation was also studied, which suggests that a population size of 5,000 may be relevant and more importantly the R² based on this size tends to stabilize (data not shown). Consequently, the R² (or its derivative Eq) for OPLS model fitting based on 5,000 profiles may serve as an indicator of equivalence between test and reference populations of at least this size.

Fig. 2.

Comparison of chi-square ratio statistics and orthogonal partial least square analysis with respect to profile comparison. a. Flowchart of the chi-square ratio statistics developed by the PQRI working group. b. Flowchart of the orthogonal partial least square analysis developed in our group

Orthogonal Partial Least Square Analysis of Test and Reference Profiles

Profiles generated by Monte Carlo simulation were analyzed by OPLS analysis as described in methods. OPLS places the first principal component onto the largest difference between test and reference profiles. The successive principal components will span the difference which is not represented by the preceding component (15). Therefore, OPLS score plot consisting of the first two components provides a visual impression of the comparability between test and reference profiles. The larger the difference between the test and reference profiles, the further they are separated from each other on the first principal component. However, this separation is only a qualitative impression rather than a quantitative measure. In order to derive a semi-quantitative parameter which may serve as a measure of equivalence, R² for OPLS model fitting (based on the first principal component) was initially selected. R² represents how well the model fits the data or how much variability in the data can be explained by the model (15). R² equals to 0 if test and reference profiles are identical; on the other hand, R² approaches 1 when test profiles are completely different from reference profiles assuming a right model is used. Apart from model fitting, R² also depends on the variability in the data as will be seen in the following section where different data pretreatment methods (i.e., different treatment of the variability) were employed. Based on this rationale, we define a parameter Eq = 1 − R², which may be considered as a measure of equivalence or comparability for the test and reference profiles. Strictly speaking, Eq is not a statistical value that can be used for statistical testing but rather a semi-quantitative value defined by us for the purpose of interpretive evaluation of APSD profiles.

Studying 55 Realistic Scenarios with Orthogonal Partial Least Square Analysis

Based on the description above and in the methods, OPLS analysis of 55 realistic scenarios was carried out with different data pretreatment methods. The absolute mass deposition data can be used as is or normalized to percent mass deposition data. All the data were mean-centered to avoid greater deposition on particular sites dominating the whole distribution. To account for the variance on each deposition site, in another word to weigh each site, two scaling methods were employed. One is unit-variance (UV) scaling in which the base weight is computed as the reciprocal of standard deviation and the other is Pareto scaling which gives the weight of the reciprocal of square root of standard deviation (15). Pareto scaling is between no scaling and UV scaling and gives the variable under evaluation a variance equal to its standard deviation instead of unit variance. The effect of both scaling methods was investigated comprehensively.

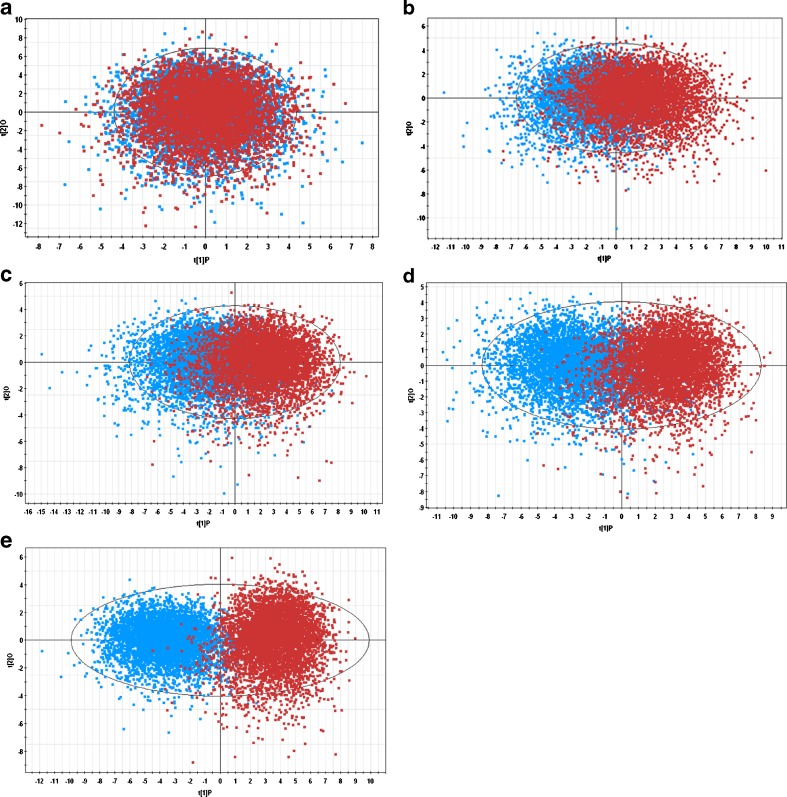
Before performing OPLS analysis on all realistic scenarios, we carried out a test analysis on the feasibility of this method. In Fig. 3a, Monte Carlo simulations were performed twice (5,000 for each) based on parameters from reference profiles in scenario 1a. The first simulation generates 5,000 reference profiles and the second simulation generates another 5,000 reference profiles yet considered as test profiles. Predictably, OPLS analysis on such reference and test profiles should yield a R² approaching 0 and both profiles should be completely mixed without any separation on the first principal component in the score plot. Indeed, we observed the same phenomenon as shown in Fig. 3a. Then OPLS analysis was performed for all realistic scenarios. Figure 3b–e represents such analysis for scenario 1a–1d, which was considered by the working group with decreasing similarity between test and reference profiles. OPLS analysis showed the same trend as evidenced by more and more separation between profiles on the first principal component in the score plot (Fig. 3b-e).

Fig. 3.

Score plot of orthogonal partial least square analysis to compare reference and test profiles generated by Monte Carlo simulation (5,000). Each data point in the score plot represents a whole profile (deposition on all sites). Reference profiles are colored blue and test profiles are colored red. a Reference profiles from scenario 1a were compared with itself (two separate simulations). b–e Reference profiles were compared with test profiles from scenarios 1a, 1b, 1c, and 1d respectively

Effect of Different Data Pretreatment Methods on the Performance of Orthogonal Partial Least Square Analysis

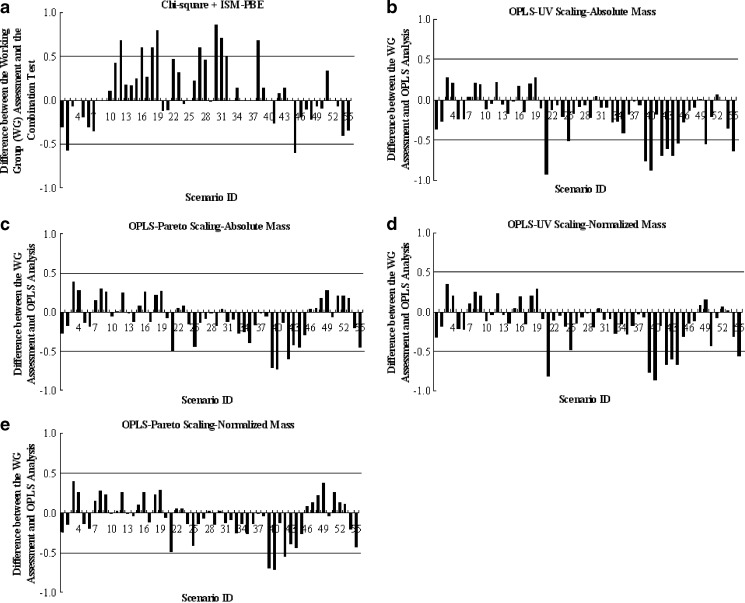
The Eq value (defined as 1 − R²) for each scenario computed by OPLS analysis based on different data pretreatment methods, the probability of equivalence derived from the combination test (chi-square + ISM-PBE), and the working group evaluation of equivalence are all tabulated in Table I. It has been proposed by the working group that agreement to within 50% (or 0.5) of the overall frequency of equivalence declarations between the working group and the combination test was interpreted as adequate for the statistical procedure to make correct decisions (14). In cases where the differences were more than 0.5, the combination test was considered not be able to make the correct decisions and inputs from reviews’ experience were necessary to determine APSD equivalence. Similarly, we extended this criterion to the performance of the OPLS analysis (i.e., the difference between Eq value and the working group assessment less than 0.5 was considered adequate). The differences between the working group evaluation and the combination test are plotted in Fig. 4a. The difference between the working group assessment and OPLS analysis for each of the data pretreatment methods are plotted in Fig. 4b–e. We noticed that OPLS analysis with Pareto scaling works better than UV scaling as evidenced by less inconsistencies no matter whether absolute or normalized mass was used. However, UV scaling on normalized mass works better than the same scaling on absolute mass. The effect of different scaling methods on multivariate data analysis has been studied in other fields (18). Van de Berg showed in his metabolomic study that Pareto scaling, compared to unit-variance scaling, was more stable in terms of generating reliable rank of the most important metabolites (19). Noda examined two scaling techniques (Pareto scaling vs. unit-variance scaling) to enhance two-dimensional correlation Raman spectra and concluded that Pareto scaling was able to circumvent the amplification of noise by retaining a portion of magnitude information (20). Therefore, it is not to our surprise that Pareto scaling works better than UV scaling since the magnitude information about the mass deposition on each site was retained. And this magnitude information was not changed from absolute to normalized mass deposition data when used with Pareto scaling. However, the inaccuracy of mass deposition may be amplified to a different extent with or without normalization since the magnitude information was completely lost in unit-variance scaling. This may provide a possible explanation for the different performance on normalized or absolute mass data with UV scaling. Finally, we compared (Fig. 5) the performance of the combination test with that of OPLS analysis based on Pareto scaling by chi-square statistical test according to the criterion proposed in the methods. The p value (0.036 < 0.05) suggested that multivariate data analysis may be more indicative than the combination test for the purpose of interpretive evaluation of comparability or equivalence of APSD profiles.

Table I.

Equivalence Value Determined from Different Analysis Methods and the Working Group Evaluation

Scenario	UV-Abs	Par-Abs	UV-Nor	Par-Nor	Chi-2 + ISM	WG
1a	0.64	0.73	0.68	0.77	0.70	1.00
1b	0.53	0.62	0.60	0.65	0.22	0.79
1c	0.34	0.46	0.42	0.47	0.01	0.07
1d	0.20	0.28	0.20	0.26	0.00	0.00
1aa	0.76	0.86	0.79	0.87	0.81	1.00
1bb	0.55	0.61	0.56	0.60	0.48	0.79
1cc	0.39	0.51	0.47	0.51	0.01	0.36
1dd	0.20	0.29	0.25	0.28	0.00	0.00
1ee	0.18	0.25	0.20	0.22	0.00	0.00
2a	0.67	0.74	0.68	0.78	0.89	0.79
2b	0.45	0.51	0.46	0.53	0.92	0.50
2c	0.43	0.46	0.44	0.47	0.89	0.21
2aa1	0.66	0.70	0.67	0.70	0.88	0.71
2bb1	0.47	0.51	0.49	0.60	0.80	0.64
2cc1	0.48	0.57	0.54	0.60	0.74	0.50
2dd1	0.46	0.55	0.48	0.54	0.89	0.29
2aa2	0.49	0.52	0.49	0.53	0.90	0.64
2bb2	0.48	0.51	0.49	0.52	0.89	0.29
2cc2	0.41	0.41	0.42	0.43	0.94	0.14
4a	0.90	0.93	0.91	0.94	0.88	1.00
4b	0.07	0.51	0.19	0.51	0.89	1.00
4c	0.08	0.26	0.11	0.26	0.68	0.21
4d	0.07	0.21	0.09	0.19	0.45	0.14
5a	0.72	0.78	0.74	0.80	0.89	0.93
5b	0.35	0.42	0.39	0.44	0.86	0.86
5c	0.12	0.16	0.15	0.16	0.50	0.29
7a	0.21	0.21	0.23	0.23	0.89	0.29
7b	0.44	0.48	0.49	0.53	0.95	0.50
7c	0.71	0.76	0.74	0.79	0.92	0.93
10a	0.18	0.17	0.17	0.16	1.00	0.14
10b	0.20	0.17	0.20	0.17	1.00	0.29
10c	0.41	0.41	0.41	0.41	1.00	0.50
10d	0.71	0.73	0.73	0.74	1.00	1.00
11a	0.36	0.39	0.49	0.51	0.78	0.64
11b	0.59	0.62	0.72	0.74	1.00	1.00
11c	0.82	0.84	0.83	0.87	1.00	1.00
12a0	0.05	0.06	0.05	0.06	0.07	0.07
12a1	0.07	0.09	0.07	0.10	0.82	0.14
12a2	0.10	0.15	0.10	0.16	1.00	0.86
12a3	0.12	0.27	0.13	0.29	1.00	1.00
12b0	0.11	0.16	0.11	0.17	0.03	0.29
12b1	0.17	0.26	0.19	0.31	0.93	0.86
12b2	0.25	0.44	0.27	0.47	1.00	0.86
12b3	0.31	0.55	0.33	0.56	1.00	1.00
13a	0.46	0.71	0.69	0.74	0.40	1.00
13b	0.29	0.60	0.43	0.65	0.38	0.57
13c	0.22	0.41	0.24	0.49	0.26	0.36
13d	0.12	0.38	0.29	0.43	0.00	0.21
13e	0.07	0.35	0.23	0.44	0.00	0.07
13f	0.38	0.87	0.50	0.90	0.84	0.93
13g	0.29	0.71	0.42	0.75	0.83	0.50
14a1	0.06	0.20	0.07	0.13	0.00	0.00
14a2	0.06	0.25	0.09	0.18	0.00	0.07
14a3	0.07	0.23	0.12	0.22	0.03	0.43
14a4	0.07	0.26	0.15	0.28	0.37	0.71

Column I: scenario ID. Columns II–V: equivalence (Eq value) determined based on orthogonal partial least square analysis with different data pretreatment methods. Eq values in columns II–V are the average of three individual simulations (n = 3, 5,000 each). Column VI: likelihood of equivalence based on the combination test proposed by the US FDA and the PQRI working group. Column VII: equivalence evaluated by the working group. The likelihood of equivalence from the working group evaluation and the combination test were retrieved from Ref. (14)

UV-Abs absolute mass data were pretreated with unit-variance scaling, Par-Abs absolute mass data were pretreated with Pareto scaling, UV-Nor normalized percent mass data were pretreated with unit-variance scaling, Par-Nor normalized percent mass data were pretreated with Pareto scaling, Chi-2 + ISM chi-square ratio statistics supplemented by a population bioequivalence test for impactor-sized mass, WG working group evaluation

Fig. 4.

Differences between the working group (WG) assessment and statistical analyses based on different methods and data pretreatment. a Differences between the WG assessment and the combination test (chi-square plus ISM-PBE). b Differences between the WG assessment and the OPLS analysis based on unit-variance scaling on absolute mass data. c Same as 4b except that Pareto scaling was used. d Same as 4b but absolute mass data was first normalized to percent mass data. e Same as 4d but Pareto scaling was used. The working group evaluation and possibility of equivalence from the combination test were retrieved from Ref. (14)

Fig. 5.

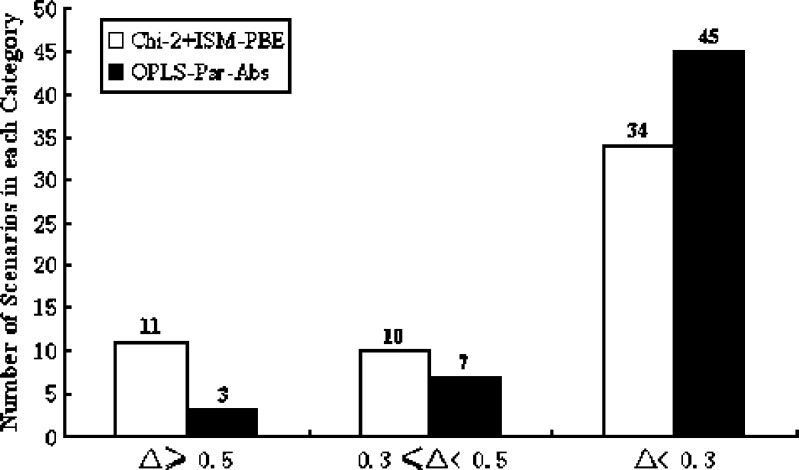
Comparison of the performance of the combination test (chi-square plus ISM-PBE) with that of orthogonal partial least square analysis based on Pareto scaling. The difference (Δ) between the working group evaluation and each of the two analysis methods was placed into three categories as labeled. The number of scenarios fall into each category was plotted in the y axis and labeled above the corresponding bar. Chi-square statistical test was then performed to compare the two methods in terms of achieving greater consistencies (Chi-Sq = 6.632, p value = 0.036). The working group assessment and the possibility of equivalence from the combination test were retrieved from Ref. (14)

Three Scenarios Mispredicted by Orthogonal Partial Least Square Analysis

When OPLS analysis with Pareto Scaling was employed, three scenarios with differences exceeding 0.5 are 12a2, 12a3, and 12b1 (Fig. 4c and Table I). An impression of equivalent test and reference profiles was given when these scenarios were reconstituted by Monte Carlo simulation (data not shown). However, OPLS analysis clearly separated the test profiles from the reference profiles in the score plot (data not shown) possibly because of very small standard deviation relative to the mean in certain deposition sites. OPLS analysis appeared to be sensitive to small standard deviation/mean ratios while at this stage no efforts have been expended in correlating the sensitivity of OPLS analysis to the standard deviation/mean ratios. On the other hand, the combination test predicts pretty well in these three scenarios (Fig. 4a and Table I).

Orthogonal Partial Least Square Analysis of Mass Deposition on Partial Deposition Sites

Comparison based on the whole deposition profiles was recommended by the FDA and PQRI working group since a change in mass deposition outside the impactor may affect the performance of the drug product (1). However, researchers are sometimes interested in only a part of the APSD profiles (e.g., mass deposition inside impactors and on the filter (21)) for two reasons: (1) there was no clear cut-off size for mass deposition outside the impactor; (2) mass deposition on these sites is important for the calculation of mass median aerodynamic diameter. Therefore, we performed OPLS analysis with Pareto scaling on mass deposition profiles inside the impactor for all 55 realistic scenarios (data not shown). Then, we compared the R² obtained from partial deposition sites with that from all deposition sites. In scenario 13c, the R² for partial sites is 0.08 as opposed to 0.51 for all sites. This difference may be explained by the greater difference between test and reference profiles outside the impactor while the difference inside the impactor is very small (Fig. 1a). In scenario 2bb2, the major difference comes from the deposition inside the impactor while little difference exists outside the impactor. The R² for partial sites is 0.46 and 0.48 for all sites. This modest increase in R² is due to a mild contribution of small difference from deposition sites outside the impactor (Fig. 1b). Our analyses indicate that OPLS analysis performed on partial deposition sites does not interfere with the performance on all deposition sites.

CONCLUSION

Multivariate data analysis may open a new way for scientists in the field of pharmaceutical aerosol sciences to evaluate the comparability or equivalence of aerodynamic particle size distribution profiles. Our study shows that orthogonal partial least square analysis coupled with Pareto scaling works best among all the data pretreatment methods investigated. It is not the intention for this article to replace the combination test proposed by the FDA and PQRI working group; rather this new method may serve as a semi-quantitative tool to evaluate particle size distribution profiles before a robust and well-established statistical test can be proposed. In addition, orthogonal partial least square analysis should be performed with caution in certain situations where the standard deviation/mean ratios are relatively small where the combination test or more statistically relevant test should be considered.