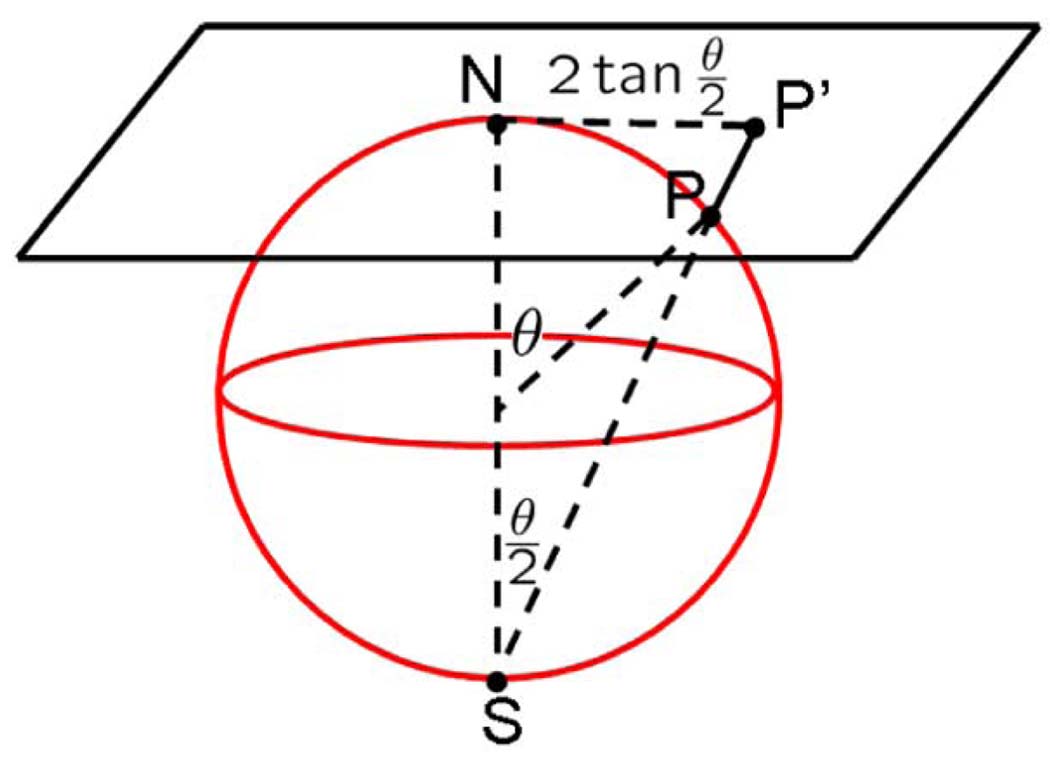
Fig. 3.

Stereographic dilation. Correspondence between the spherical surface and tangent plane is established via stereographic projection: point P on the sphere is mapped to the point P′ on the tangent plane of the north pole. This allows a spherical function f(θ ϕ) to be mapped onto the tangent plane. The usual dilation is then performed on the tangent plane. The resulting dilated function is mapped back onto the sphere via stereographic dilation: (1/a)f(2 tan⁻¹ ((1/a) tan(θ/2));ϕ). The normalization factor (1 / tan² (θ/2))/(1+ ((1/a) tan (θ/2))²) is added to conserve the inner product between dilated functions.