Table 2.

Comparisons between empirical networks and clustered random networks

Generated Network Type	N	<d >	<d2 >	T		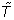Diam	r	Q
Little Rock Foodweb Interactions	183	27.3	1215	0.38 [0.009]	0.58 [0.0]	4 [0.0]	-0.09 [0.15]	0.11 [-0.21]
Yeast Protein Interactions	4713	6.3	152	0.07 [0.01]	0.18 [0]	12.5 [0.5]	0.11 [0.38]	0.39 [-0.10]
C. elegans Metabolic Interactions	453	8.9	358	0.14 [0.02]	0.60 [0]	6 [-1]	-0.19 [0.04]	0.29 [-0.09]
Vancouver Epidemiological Contacts	2627	13.9	265	0.09 [0]	0.14 [0]	6 [0]	0.15 [-0.4]	0.28 [-0.15]
US Air Traffic Links	165	38.0	2765	0.58 [0]	0.97 [0]	3 [0]	-0.55 [0]	0.11 [-0.01]

For each empirical network, we generated 25 random graphs constrained to have the observed degree sequences and Soffer-Vasquez transitivity values. The table reports average values of several network statistics for the clustered random graphs: network size (N), mean degree (⟨d⟩), mean squared degree (⟨d²⟩), Soffer-Vasquez clustering coefficient (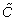), Soffer-Vasquez transitivity (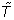), maximum shortest path length between any two nodes (diam), degree correlation coefficient (r), and modularity (Q). The value given in brackets is the deviation of the ensemble mean from the corresponding statistic for the empirical network. (A positive deviation indicates that the ensemble mean was greater than the empirical statistic and vice versa.) Deviations are not listed for N, ⟨d⟩ and ⟨d²⟩ as network size and degree sequence are constrained by our algorithm to match the empirical networks perfectly.