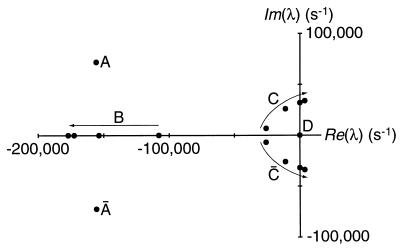
Figure 2.

Parameter dependence of the system’s eigenvalues (λ). The eigenvalues determined for four values (108, 140, 220, and 300) of the stereociliary number, N_S, are represented on the complex plane. The points designated B, C, and C̄ demonstrate the functional dependence of the system on N_S; the arrows indicate the progression of eigenvalues with increasing values of this parameter. The angular frequency at the Hopf bifurcation for C and C̄, ±32,000 s⁻¹, corresponds to a characteristic frequency of ∼5 kHz. Point D, which represents the conservation of state probability in the channel-gating cycle, remains at the origin. The conjugate pair A and Ā are independent of N_S and also appear stationary. An additional conjugate pair of eigenvalues, those farthest to the left, have been omitted to permit display of the remaining points on an informative scale. The system is characterized by an eighth-degree characteristic polynomial that precludes a closed form for the eigenvalues; numerical evaluation was therefore necessary. The stability analysis and simulation programs were written in mathematica and executed on a Macintosh Quadra 800 computer (Apple Computer, Cupertino, CA) or an Indigo Impact 10000 computer (Silicon Graphics, Mountain View, CA).