Modeling Reaction Time and Accuracy of Multiple-Alternative Decisions

Abstract

Several sequential sampling models using racing diffusion processes for multiple-alternative decisions were evaluated using data from two perceptual discrimination experiments. The structures of the models differed on a number of dimensions, including whether there was lateral inhibition between accumulators, whether there was decay in evidence, whether evidence could be negative, and whether there was variability in starting points. Data were collected from a letter discrimination task in which stimulus difficulty and probability of the response alternatives were varied along with number of response alternatives. Model fitting results ruled out a large number of model classes in favor of a smaller number of specific models, most of which showed a moderate to high degree of mimicking. The best-fitting models had zero to moderate values of decay, no inhibition, and assumed that the addition of alternatives either affected the subprocesses contributing to the nondecisional time, the degree of caution, or the quality of evidence extracted from stimuli.

Perceptual decision making is an area of research that has had a great deal of attention over the last 10 years or so. In psychology, it has been investigated with a range of approaches, from experimental to theoretical (Bogacz, Usher, Zhang, and McClelland, 2007; Ratcliff and Rouder, 1998; Ratcliff, Van Zandt, and McKoon, 1999; Smith, 1995; Smith and Ratcliff, 2009; Smith, Ratcliff, and Wolfgang, 2004; Usher and McClelland, 2001), and it has been studied with combined theoretical and empirical approaches in neuroscience (Gold and Shadlen, 2000; Newsome, Britten, and Movshon, 1989; Salzman and Newsome, 1994; Shadlen and Newsome, 2001; Supèr, Spekreijse, and Lamme, 2001). In most of the work to date, experimental work has focused on the two-choice experimental paradigm (e.g., Ratcliff and Rouder, 1998). There has also been an accumulating body of research that has taken models of processing and extended them to multiple-choice paradigms (Bogacz et al., 2007; McMillen and Holmes, 2006; Usher and McClelland, 2004; Usher, Olami, and McClelland, 2002). But to this point in time, there are relatively few combined experimental and theoretical studies of multiple-alternative perceptual decision making. Our aim in this article is to address the lack of such studies by presenting an experiment and comprehensive theoretical analyses.¹

The growing consensus in the perceptual decision making domain is that only models that assume evidence is gradually accumulated over time can account for the full range of experimental data, namely, accuracy and both correct and error reaction time (RT) distributions. Two variants of this general class are the Wiener diffusion process model (Ratcliff, 1978, 2002; Ratcliff and McKoon, 2008; Ratcliff and Rouder, 2000) and the multiple racing diffusion processes model (Ratcliff, 2006; Smith, 2000; Usher and McClelland, 2001). In the standard diffusion process, evidence is accumulated in a single variable toward one of two decision criteria. This model is difficult to extend to multiple alternatives, although Laming (1968) and Pike (1966), for example, have offered qualitative suggestions. The model that seems most natural for the multiple-alternative paradigm assumes that evidence is accumulated in separate accumulators, corresponding to the different alternatives. In particular, the model that best exemplifies the set of features we wish to test is the leaky competing accumulator (LCA; Usher and McClelland, 2001). This model assumes stochastic accumulation of information continuously occurring over time, with leakage (decay) and lateral inhibition (competition among accumulators), with the possibility of variability in both starting point and the drift rates driving the accumulation process. The LCA model, however, has been fit to relatively few experimental data sets.

The general evidence accumulation model has been applied to a number of domains, from neurophysiological data to cognitive tasks such as memory, lexical processing, and absolute identification, to aging and impaired processing, and to consumer decision making (Boucher, Palmeri, Logan, and Schall, 2007; Brown and Heathcote, 2005; Brown, Marley, Donkin, and Heathcote, 2008; Busemeyer and Townsend, 1993; Ditterich, 2006; Gomez, Perea, and Ratcliff, 2007; Mazurek, Roitman, Ditterich, and Shadlen, 2003; Niwa and Ditterich, 2008; Ratcliff, Cherian, and Segraves, 2003; Ratcliff, Gomez, and McKoon, 2004; Ratcliff, Hasegawa, Hasegawa, Smith, and Segraves, 2007; Ratcliff and Smith, 2004; Ratcliff, Thapar, and McKoon, 2006; Ratcliff, Thapar, Smith, and McKoon, 2005; Ratcliff and Van Dongen, in press; Roe, Busemeyer, and Townsend, 2001). One of the features of models in the evidence accumulation class is that in order for them to successfully account for the full range of experimental data, they need to assume that various components of processing vary from trial to trial (Laming, 1968; Ratcliff, 1978; Ratcliff et al., 1999; Ratcliff and Rouder, 1998). These models can be contrasted with signal detection theory (SDT; Swets, Tanner Jr., and Birdsall, 1961), in which all sources of noise are combined into a single source, namely, variability in perceptual strength. For example, in the class of diffusion process models, the decision process is assumed to be variable within a trial (within trial noise) and across trials, in perceptual strength (drift rate) and starting points.

In neuroscience, Hanes and Schall (1996) were the first to convincingly argue that it is possible to relate evidence accumulation models to single-cell recording data. They suggested that rhesus monkeys’ saccadic movements were initiated if and only if the neural activity in frontal eye field cells surpassed a (constant) threshold and that RT distribution was a resultant of the stochastic variability in the rate at which neural activity grew toward that threshold. Following Hanes and Schall’s work, the neurobiology of decision making field seems to have adopted the motion discrimination paradigm to examine perceptual decision making (e.g., Ditterich, 2006; Gold and Shadlen, 2000; Heekeren, Marrett, Ruff, Bandettini, and Ungerleider, 2006; Niwa and Ditterich, 2008; Palmer, Huk, and Shadlen, 2005; Ratcliff and McKoon, 2008; Roitman and Shadlen, 2002; Salzman and Newsome, 1994; Shadlen and Newsome, 2001). In a standard motion discrimination task, a percentage of dots in a display move coherently, while the remaining dots are shuffled to random positions. Primate or human participants decide which direction in the coherent dots are moving and respond with a saccade to a target or keypress.

Several studies applied models that assumed accumulation of information toward decision criteria to experimental data from the motion discrimination task. In some of these studies (Mazurek et al., 2003; Palmer et al., 2005; Roitman and Shadlen, 2002), joint RT and accuracy were collected, but the models either were not fit to the full range of experimental data or fit relatively poorly. Because the models were not successfully fit to the range of behavioral data, it is not possible to determine whether the models need the various sources of variability in processing to account of the full range of data. Nevertheless, some of the models used only within trial noise. Models in Ditterich (2006), Niwa and Ditterich (2008), and Ratcliff and McKoon (2008), on the other hand, attempted to fit accuracy and RT distributions for both correct and error responses jointly, and so identify the different sources of noise.

Evidence accumulation models have also been related to physiological measures in humans, using both functional magnetic resonance imaging (fMRI) and electroencephalography (EEG). Heekeren et al. (2006), for example, found evidence for a decision variable existing independent of motor planning and execution. They had participants express their decision about direction of motion using two independent motor systems, oculomotor and manual, and found that four brain regions showed increased blood-oxygenation-level-dependent (BOLD) signal to high-coherence (relative to low-coherence), independent of the motor system used to express the decision. Philiastides, Ratcliff, and Sajda (2006), using a single-trial analysis of EEG data from a face-car discrimination task with human participants, found support for a time separation between perceptual processing and decision-making processing. This separation suggests that cortical networks could dynamically allocate additional processing time for difficult decisions.

In behavioral research in psychology, the study of perceptual decision making has used models that make a great deal of contact between theory and data. In particular, the sequential sampling framework has been successful in accounting for both RT and accuracy, as well as speed-accuracy trade-off effects (for reviews, see Luce, 1986; Ratcliff and Smith, 2004; Vickers, Caudrey, and Willson, 1971), continuing to be of critical theoretical interest. An exemplar of this particular modeling approach is the diffusion model proposed by Ratcliff (1978). Using a numerosity judgment task, for example, Ratcliff et al. (1999) showed that the diffusion model could explain how both correct and incorrect decisions are made, how their relative speeds change as a function of experimental conditions, and why RT distributions have their characteristic shapes. Models implementing multiple racing diffusion processes (e.g., Bogacz et al., 2007; Ratcliff et al., 2007; Usher and McClelland, 2001) not only extend well to multiple-alternative paradigms but also fit two-choice data qualitatively as well as the diffusion model (Ratcliff, 2006; Ratcliff and Smith, 2004; Ratcliff et al., 2005).

The evidence accumulation models have a major advantage over static models of decision making, in that they allow for several sources of variability that occur in different components of processing and that are identifiable (Ratcliff and McKoon, 2008; Ratcliff and Tuerlinckx, 2002). For example, there can be variability in perceptual strength (variability in drift rate across trials), variability in starting points of the process or variability in decision criteria, variability in the decision process itself (within trial noise), and variability in the duration of other processes (encoding and response output). The ability of these models to identify such variability sources is a major advance because they allow noise is processing to be separated into different points in the stream of processing, from encoding to decision. If our experimental and theoretical work is to be related to physiological measures (i.e., EEG, fMRI, magnetoencephalography, or single-cell recording), then we need the ability to separate different sources of variability (e.g., Ratcliff, Philiastides, and Sajda, 2009).

Our aim in this article is to present an experiment in which the number of alternatives is manipulated along with the difficulty of the decision. This will allow us to test whether the data support one or many of a range of possible model features. What we aim to learn about perceptual decision making from this study is whether these various architectural features are necessary. In particular, is lateral inhibition between alternatives needed? Does the evidence in the accumulators decay the more evidence is accumulated? In addition, the modeling will allow us to determine which sources of variability play an important role in processing.

We present empirical data from a multiple-alternative paradigm and report tests of a number of racing diffusion process models that differ on a number of dimensions, with the various combinations of these dimensions leading to 384 possible models. We exclude most of them in preliminary analyses and report fitting details of 16 models. More specifically, we report data collected from two experiments involving a letter discrimination task that used 2, 3, or 4 response alternatives. In the first experiment, difficulty of the decision was manipulated by changing the discriminability of the stimuli and, in the second, by varying the proportion of stimuli corresponding to the different responses. In the end, we describe what properties were found in the best-fitting models and examine the impact of increasing number of alternatives on the two manipulations (difficulty and proportion).

Hick’s Law

In early investigations of the impact of increasing the number of alternatives, Hick (1952) and Hyman (1953) described evidence to support that MRT should increase with number of alternatives. If the stimuli have equal probability, this is currently viewed as a well-established fact (e.g., Luce, 1986). Hick further noted that this relationship was best fit by

$$\mathit{MRT}=A+Blog(n+1)$$ (1)

Several studies following Hick’s paper presented results that conformed to Eq. 1 or to a variant, replacing (n + 1) with n, both commonly referred to as Hick’s law or as the Hick-Hyman law (see Welford, 1980, p. 73–77, for a survey of the original Hick’s law and variants). Models of the type we evaluated are capable of producing MRTs that conform to Hick’s law. In free response protocols, for example, McMillen and Holmes (2006) showed that leaky accumulator models with absolute threshold implementations perform nearly optimally for moderate (and approximately equal) values of decay and inhibition, and error rates larger than 10%. Under these circumstances, predicted MRTs conform to Hick’s law, and this correspondence is found so long as all accumulators in the model receive equal levels of noise (see also Bogacz et al., 2007). The models reported in what follows all assume equal levels of noise for all accumulators.

Parenthetically, by defining MRT in terms of signal-to-noise ratio a/c, optimal performance is achieved when

$$\mathit{MRT}={\left(\frac{c}{a}\right)}^2\left\{log\left(\frac{1}{ER}\right)+\frac{{(h_{n-1}^{\ast })}^2}{2}\left[1+\sqrt{1+\frac{4}{{(h_{n-1}^{\ast })}^2}log\left(\frac{1}{ER}\right)}\right]\right\}+o(1),$$ (2)

where $h_{n-1}^{\ast }$ is the expected value of the (n − 1)^st standard normal order statistic and ER is the error rate (cf. McMillen and Holmes, 2006, Eq. 37).

Models

Sequential sampling models have been developed and successfully applied to cognitive tasks, but they usually involve two alternatives. For this project, we investigated multiple-alternative extensions for some members of the sequential sampling family of models. In 2004, Ratcliff and Smith reported an evaluation of four widely used sequential sampling models: the Wiener diffusion model (Laming, 1968; Link, 1975; Ratcliff, 1978, 1981, 1985, 1988a); the Ornstein-Uhlenbeck (OU) diffusion model (Busemeyer and Townsend, 1992, 1993; Smith, 2000); Vickers’ accumulator model (LaBerge, 1962; Smith and Vickers, 1988; Vickers, 1970); and the Poisson counter model (Smith and Van Zandt, 2000; Townsend and Ashby, 1983). Although the Wiener diffusion process model produced the best fits to the 2-choice RT data from three experiments against which these four models were tested, an extension of this model to multiple-alternative paradigms is not straightforward. However, Ratcliff and Smith also reported that three other models, whose architectures are suitable to multiple alternatives, mimicked the Wiener diffusion process model and produced fits almost as good as the Wiener diffusion process model’s. These models were Usher and McClelland’s LCA model (2001) and two other models assuming racing diffusion processes, either with absolute stopping criteria and decay or with relative stopping criteria (i.e., max vs. next; see Ratcliff, 2006; Ratcliff, Thapar, Smith, and McKoon, 2005, for reports of similar results).

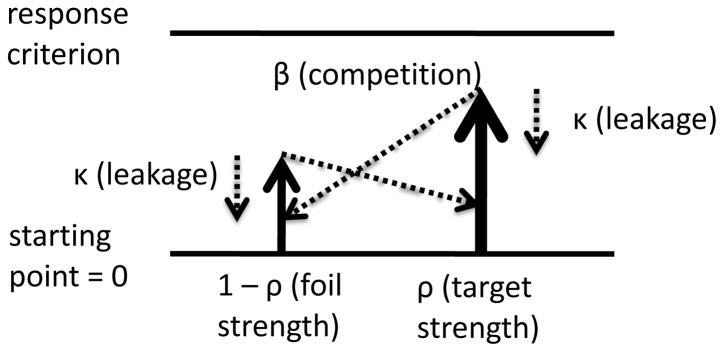
Usher and McClelland’s LCA model (2001) assumes stochastic accumulation of information continuously occurring over time, with leakage (decay) and lateral inhibition (competition among accumulators). There is one accumulator implementing a diffusion process for each response alternative, and a response is made when an accumulator reaches its respective decision criterion (see Figure 1). The rate at which one accumulator approaches its criterion is determined by the input from the stimulus (ρ), the decay (κ), and the lateral inhibition (β). Inhibition increases as the amount of information increases in the other accumulators, and the size of decay increases as information in the accumulator increases. Accuracy and RT are modeled simultaneously, and the growth of evidence in the accumulators is governed by

Figure 1.

The LCA model with two accumulators. Free parameters of the model are: criteria (c₁ and c₂); decay (κ); inhibition (β); noise in the accumulation process (σ); starting point (sp); and input strength (ρ). One could also include range of variability in starting point (s_sp), a nondecisional component (t_er), and variability in t_er (s_t).

$$d{x}_i=[{\rho }_i-\kappa x_i-\beta \sum _{j\ne i}{x}_j]\frac{dt}{\tau }+{\xi }_i\sqrt{\frac{dt}{\tau }},$$ (3)

where x_i takes max(x_i, 0)—remaining non-negative—and ξ represents standard deviation in noise in the accumulation process (cf. Usher and McClelland, 2001, Eq. 4). As in Usher and McClelland, in our implementations of this model and other variants, τ was set such that $\frac{dt}{\tau }$ corresponded to 10-ms steps. Input-strength parameters were constrained so that Σ_iρ_i = 1.

In order for the LCA model to predict errors faster than correct responses (e.g., in very easy conditions), Usher and McClelland (2001) assumed rectangularly distributed (with zero minima) starting points for the accumulators, following Laming (1968) and Ratcliff et al. (1999). In all the racing diffusion process models we considered, nondecisional components (e.g., stimulus encoding and motor response processes) are combined into a single random variable, t_er, which is assumed to vary across trials. In the models, this nondecisional component takes values from a rectangular distribution with mean T_er and range s_t, and the predicted MRT is the mean time it takes the decision process to terminate plus the nondecisional component.

Models to Fit the Data

There are 384 racing diffusion process models we could produce from all possible combinations of the assumptions we presented above. We summarize the various theoretical options below (which have all been used or proposed previously in the literature), followed by brief discussions about the theoretical issues of process or representation associated with them within the framework of the LCA model.

1. Decaying vs. non-decaying accumulation. For κ > 0 in Eq. 3, evidence in any accumulator decays by an amount proportional to the amount of evidence in it. The presence or absence of decay is chiefly an architectural issue. As reported in Smith (1995), the spontaneous decay of some proportion of the accumulated signal inherently bounds the sensitivity of the decision stage.

2. Competing vs. independent accumulation. For β > 0 in Eq. 3, accumulation of evidence to any accumulator is inhibited in proportion to the amount of evidence accumulated at this point by its competitors. The assumption that one alternative influences the accumulation of evidence for competing alternatives is a plausible processing assumption discussed by Usher and McClelland (2001), who noted that the use of lateral inhibition enables the emulation of relative-evidence diffusion processes while using an absolute threshold criterion, allowing the model to be applied equivalently to two- and multiple-choice paradigms (p. 552).

3. Starting-point variability vs. identical starting points. Adding variability in starting points allows random initial biases toward one of the alternatives (e.g., Laming, 1968), making it a crucial feature in accounting for fast error responses in the data. Variability in starting point can be modeled in two ways. In its simplest form, each accumulator starts from a random point, drawn from a uniform distribution between 0 and a limit determined by a free parameter (s_sp). In an alternative form, starting points are negatively correlated, as in Ratcliff et al. (2007). In the latter case, a number x is randomly selected from a uniform distribution between 0 and s_sp/2, and one accumulator is set to start at (s_sp/2 + x), while the other accumulators start at (s_sp/2 − x).

4. Unbounded vs. bounded evidence accumulation. In racing accumulator models, it is often assumed that activity cannot fall below zero. This assumption is usually justified by appeal to neural plausibility, but from a mathematical point of view, one could relax the bounded evidence accumulation assumption by allowing accumulators to take on negative values.

5. One vs. three nondecisional-component parameters. As noted above, all models we considered assumed that the durations of all components of processing other than the decision component are combined into a single random variable that varies across trials. This non-decisional component is commonly assumed to include encoding and motor-response times. As more alternatives are added, it is possible that some motor component such as motor preparation slows down. Thus, nondecisional component can be assumed to differ with number of alternatives (i.e., 2, 3, or 4 alternatives), resulting in three additional free parameters in the model. Or it can be the same across number of alternatives, adding a single free parameter to the model.

6. One vs. three decision criterion parameters. Models can have either one single value for all the decision criteria for all numbers of alternatives, or different parameters, one for each number of alternatives involved in the decision. Since we are unaware of any other work that fit empirical multiple-alternative data and established how decision criterion should be structured, we must test this one empirically. Psychologically, it is plausible to have higher degree of caution in conditions involving higher number of alternatives.

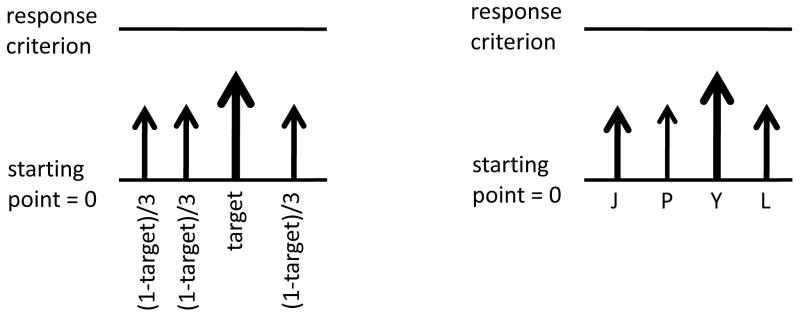
7. Target-foil vs. accumulator-specific input-strength parameters. Two assumptions regarding input-strength parameters can be made. First, the letter corresponding to the correct alternative in each trial is modeled by one (target) input strength, and the other letter alternatives have another (foil), identical input strength (see Figure 2). Second, each letter alternative in a letter discrimination task can use a separate input-strength parameter so that accumulators are assigned to specific letters. In all cases, it is assumed that the input-strength parameters add to 1 (cf. Usher and McClelland, 2001).

Figure 2.

Left panel shows a race among four accumulators driven by a single free parameter, capturing the target stimulus strength. Right panel shows a race among four accumulators driven by four input-strength parameters (if constrained to sum up to 1, this race will be governed by 3 free parameters).

In addition, input-strength parameters can be assumed to be the same or differ across number of alternatives, leading to one or three sets of target-foil pairs of parameters or one or three sets of four letter-specific parameters. Input-strength can also be assumed to vary across difficulty (or bias) levels, multiplying the number of input-strength parameters by three. These assumptions are summarized below:

1. Three input-strength parameters. One for targets in 2 alternatives (with the competitor’s strength defined as the unit minus the target input-strength); a second for targets in 3 alternatives (with the two competitors equally sharing the equivalent of the unit minus the target input-strength); and a third for targets in 4 alternatives (with the three competitors equally sharing the equivalent of the unit minus the target input-strength).

2. Nine input-strength parameters. As in (a), but allowing for a different parameter in each level of difficulty (or bias) within each number of alternatives. That is, there were 3 target parameters among 2 alternatives—one for easy trials, a second for medium-difficulty trials, and a third for difficult trials—, as well as 3 target parameters among 3 alternatives and 3 other target parameters among 4 alternatives.

3. Twelve input-strength parameters. One set of three input-strength parameters as in (a) for each of the four possible target response letters. For example, among 2-alternative trials, one set of parameters modeled trials in which P was the target response and another set modeled trials in which L was the target response.

4. Thirty six input-strength parameters. One set of nine input-strength parameters as in (b) for each of the four possible target response letters, akin to (c).

Experiments 1 and 2

We collected data using a multiple-alternative letter discrimination task, with number of alternatives ranging from 2 to 4 across blocks. Participants saw one letter in each trial, embedded in static background noise, and indicated their response by depressing the corresponding key.

We chose two manipulations: perceptual difficulty (Experiment 1) and target frequency (Experiment 2). These were chosen because we wanted to have manipulations of different cognitive processes that could lead to changes in both accuracy and RT in a relatively wide range, which, individually, could potentially be captured by a single parameter in the models. These manipulations have been successfully used to test models, and their effects have been discussed in the literature for quite some time (e.g., Hyman, 1953; Swensson, 1972, for stimulus frequency and perceptual difficulty, respectively). In short, high-quality stimuli are expected to have an advantage over low-quality stimuli, as well as high-probability stimuli are expected to have an advantage over low-probability stimuli (Thomas, 2006).

Specifically, perceptual difficulty was chosen because task difficulty is also affected by the manipulation of number of alternatives. Thus, it was important to determine which factors were responsible for behavioral changes caused by both an increase in task difficulty due to the stimulus manipulation and due to the manipulation of the number of alternatives. Target frequency has been used in studies of participants’ bias, created by the expectation of certain targets over others. Bias toward one response causes increased accuracy and faster RTs. With this manipulation we could investigate whether the effects of adding alternative interacts with that of bias.

Participants

Five undergraduate students from the Ohio State University’s community took part in the study. All participants reported normal or corrected-to-normal vision. Each participant ran a series of 45- to 50-minute sessions, for each of which they were compensated $10.00. Participants 1 through 3 participated in both experiments—Participants 1 and 3 ran Experiment 1 (4 sessions) followed by Experiment 2 (3 sessions), whereas Participant 2 ran the reverse order (6 sessions in Experiment 2 and 5 sessions in Experiment 1). Participant 4 ran only Experiment 1 (5 sessions), and Participant 5 ran only Experiment 2 (6 sessions).

Apparatus and Procedure

The experiments were run on personal computers running Linux operating system with a customized real-time system. Computers were connected to a 17″ monitor with resolution of 640×480 pixels and a standard 102-key keyboard, whose numeric keypad was altered to the arrangement shown in Figure 3.

Figure 3.

Response-key arrangement onto the numeric keypad of a standard keyboard. Dashed underscores represent absence of key.

We chose P, Y, J, and L as stimulus letters based on work by Gilmore, Hersh, Caramazza, and Griffin (1979). Gilmore et al. used a letter discrimination task to determine the frequency with which (capital) letters of the alphabet were confused with each other. We considered as stimulus candidates sets of 4 letters that were confused with one another less than 2.5% of the time, did not sound alike, and used about the same number of pixels on the computer monitor. We imposed these restrictions so that models with target-foil input-strength parameters were plausible models (see section Models to Fit the Data). Pilot runs with Z, H, F, and Y, for example, showed that participants were quicker to respond to Z than to other letters. In subsequent debriefing, participants reported to be first looking for the diagonal in the letter Z, and then for the angle atop the letter Y in order to make their response. If those searches failed, they reported deciding between H and F. No similar strategy was reported for the set P, Y, J, L.

In both experiments, a stimulus display was constructed by writing a white letter on a black background and flipping a proportion of the pixels on the screen from black to white and vice versa (e.g., Ratcliff and Rouder, 1998). We informed participants that they would perform a simple decision task with multiple alternatives and they were to identify an (approximately 90×90-pixel) letter appearing in a 320×200-pixel window in the center of the screen. The stimulus was displayed after the participants depressed the middle key, ‘5’, and they used the same finger, either the index finger or the middle finger of their right hand, to press the response key corresponding to the letter. The stimulus remained on the screen for up to 160 ms. That is, if participants released the 5-key in less than 160 ms, the stimulus was taken off the screen immediately after the 5-key release, otherwise, stimulus was on for 160 ms. Reaction time was measured from stimulus onset to release of the 5-key and the choice of response key was also recorded. Participants received a ‘Too slow’ feedback message every time they took longer than 225 ms to depress a response key after releasing the 5-key. In order to discourage participants from anticipating their responses, they were given a ‘TOO FAST’ warning message for every release occurring less than 100 ms after stimulus onset. In Experiment 2, in which anticipatory responses might occur more often, the ‘TOO FAST’ message was displayed for releases faster than 250 ms, 300 ms, and 350 ms for 2-, 3-, and 4-alternative blocks, respectively.

RT was measured from stimulus onset to the release of a key, prior to movement to any of the equally spaced response keys (cf. Figure 3) indicating the choice. This contrasts with Merkel’s 10-alternative design (in Hick, 1952), in which participants rested their 10 fingers on a series of 10 keys and indicated their response by depressing a key with its corresponding finger. This use of 10 keys provides no safeguard against the possibility that a participant may be able to hit keys more quickly with some fingers than others (although the different speeds associated with different fingers may be small).

In short, the combination of very short post-key-release movements, the feedback triggered by relatively long post-key-release times, and the removal of stimulus from display after key release (when applicable, viz., responses shorter than 160 ms) were safeguards in place to prevent decision processes from occurring past our recorded decision times (see Smith and Carew, 1987, for possible participants’ strategies that may distort the measurement of RT in a similar paradigm than ours). It is nevertheless possible that, in our design, some cognitive processes may still be taking place post key release (e.g., self monitoring), but we know of no evidence to suggest that these processes do not occur when responses are made by key press as well or that they are part of the decision processes we model.

Although the mapping from letter to response key did not change across trials, at the start of each trial, the response-key arrangement was presented on the screen (see Figure 3), simply as a reminder for the participants. In blocks with fewer than 4 alternatives, a pound sign replaced unused alternatives. Figure 4 illustrates the timeline of a trial.

Figure 4.

Trial timeline. Initial screen with instructions and the response-key arrangement remained on until 5-key was depressed. Then fixation point was displayed for 300 ms, followed by stimulus presentation for 160 ms. A blank screen followed and remained on until participant’s response, after which next trial began.

Design

Two 3×3 designs, detailed below, were used. In each experiment, a session was composed of 36 blocks of 60 trials each. Data from entire sessions were left out of the analyses when participants were still familiarizing themselves with the tasks and procedures. Participants 1 and 3 also ran some pilot sessions, and hence none of their sessions were excluded from our analyses. Participant 2’s first 2 sessions in Experiment 2 and first session in Experiment 1 were excluded. Participant’s 4 initial session was also excluded, as well as Participant’s 5 initial 3 sessions.

Experiment 1: Difficulty

In Experiment 1, factors were difficulty (within blocks) and number of alternatives (across blocks). In each session there were twelve 2-alternative blocks, twelve 3-alternative blocks, and twelve 4-alternative blocks, randomly intermixed. In each block, twenty easy trials, twenty medium trials, and twenty difficult trials (i.e., respectively flipping 28.5%, 32.1%, or 36.1% of the pixels from the white letter written on a black background from black to white and vice versa) were presented, and participants were informed of the equal proportions of the different levels of difficulty.

Experiment 2: Proportion

In Experiment 2, factors were stimulus proportion (across blocks) and number of alternatives (across blocks). There were three conditions in which one letter was chosen to be the high-proportion alternative (versus the other low-proportion letters): no-, low-, and high-bias conditions. Specifically, proportions were: 30:30, 45:15, and 51:9, for no-, low-, and high-bias conditions in 2-alternative blocks; 20:20:20, 36:12:12, and 45:8:7, for no-, low-, and high-bias conditions in 3-alternative blocks; and 15:15:15:15, 30:10:10:10, and 40:7:7:6, for no-, low-, and high-bias conditions in 4-alternative blocks. All letters had an equal number of trials as the high-proportion stimulus. Stimulus difficulty was held constant: 31.6% of the pixels from the white letter written on a black background were flipped from black to white and vice versa in all trials. In a session, there were 12 no-bias blocks, 12 low-bias blocks, and 12 high-bias blocks. Thus, among 4-alternative blocks, each letter was the high-bias target once. Before each block, participants were told how many times each alternative would appear in that block. We instructed participants to use that information to their advantage, but not to anticipate their responses.

Results

In this section, we present data from the two experiments. In the immediately following section, we present the model fits to data.

Number of Alternatives and Hick’s Law

Figure 5 shows mean correct RT plotted as function of number of alternatives averaged over Experiment 1 (left panel) and Experiment 2 (right panel). Results showed an increase in mean correct RT that is consistent with Hick’s law,² although this relationship will not allow discrimination among the models because most will be able to predict this pattern. Slight decreases in accuracy with an increase in number of alternatives were also observed (see below), consistent with previous reports (e.g., Lacouture and Marley, 1995).

Figure 5.

Theoretical Hick’s law predictions vs. individual mean correct RT (ms) in both experiments. Note that data from middle and right columns in Experiment 2 (right panel) are not expected to conform to Hick’s law because, by design, stimuli are not equiprobable.

Experiment 1

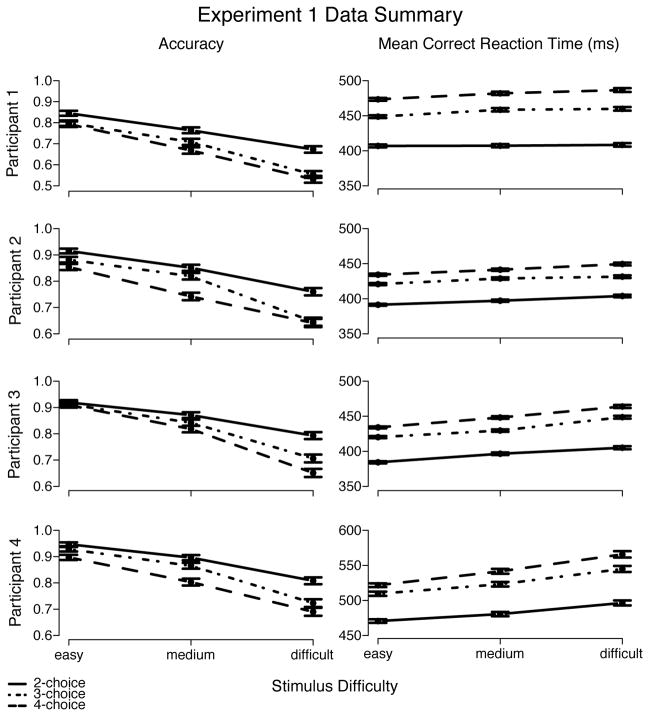
Extreme fast and slow responses were eliminated from analyses using cutoffs. The lower cutoffs was chosen to be the point below which participants performed at chance level. The upper cutoffs was chosen to eliminate very slow outliers (e.g., responses 200 ms or slower than the next fastest response) or below-chance slow responses. Averaged over participants, in Experiment 1, the mean lower cutoffs were 253 ms, 285 ms, and 298 ms, whereas the mean upper cutoffs were 787 ms, 900 ms, and 950 ms, for 2, 3, and 4 alternatives, respectively.³ Excluding data points in this way eliminated approximately 0.9% of the data. Results from Experiment 1 showed that, for all participants, mean correct RT increased and accuracy decreased as either number of alternatives or difficulty increased (see Table 1 and Figure 6).

Table 1.

Analysis of Variance for Experiment 1

Source	df	F	η2	p
Participants	3	285.99**	.68	.00
Number of alternatives (A)	2	171.25**	.27	.00
Difficulty (D)	2	21.04**	.03	.00
A × D	4	0.44	.00	.78
Residuals	24	(1470)

Note. Participants is a between-subjects factor, whereas number of alternatives and difficulty are within-subjects factors. Values enclosed in parentheses represent mean square errors.

^**p < .001.

Figure 6.

Left panel shows that accuracy decreased with both increased number of alternatives and increased task difficulty. Right panel shows that mean correct RT increased with both increased number of alternatives and increased task difficulty. Error bars mark one standard error below and above each point.

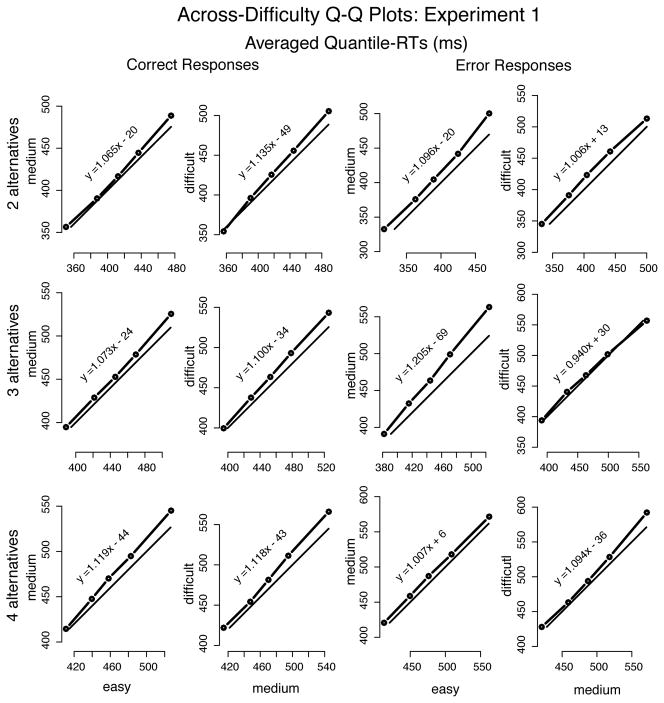
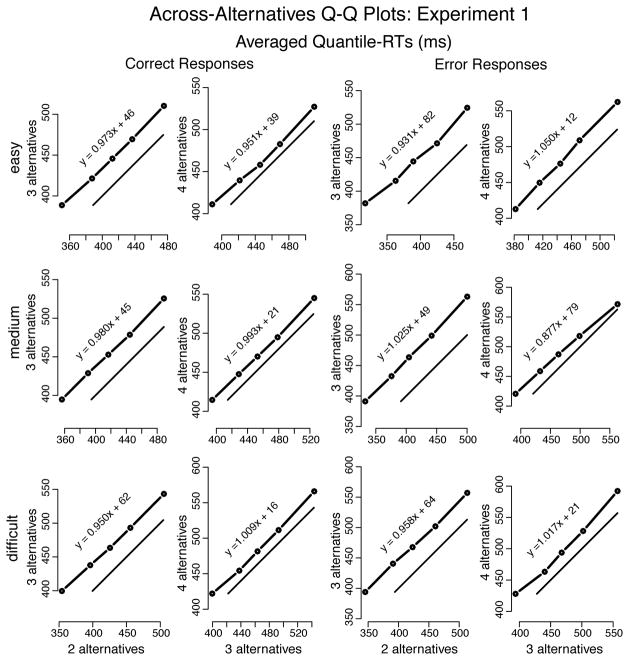
Plotting quantile RT vs. quantile RT (Q-Q plots), averaged across participants, showed approximately linear relationships between conditions (cf. Ratcliff and McKoon, 2008), whether across difficulty levels (Figure 7) or across number of alternatives (Figure 8). Linearity in Q-Q plots implies invariance in distribution shape between conditions. The closer the Q-Q line is to the x = y line, the closer to identical the distributions; a line (approximately) parallel to and above x = y (i.e., slope around the unit) implies a shift of the entire distribution in the y condition relative to the x condition (e.g., Figure 7, 2 alternatives, error responses, medium vs. difficult).

Figure 7.

Quantile-Quantile plots drawn from averaging the individual quantiles computed for each participant in Experiment 1 (represented by the dots connected to the thicker solid lines). The thinner solid lines represent x = y. Equation y = ax + b (a =slope; b =intercept) is the regression-line of y on x—slopes near the unit indicate nearly identical distributions between y and x; slopes greater than the unit show spreading of the tail in y vs. x; and slopes below the unit show spreading of the lading edge of the y distribution in comparison to x. Plots show very little difference in the shape of RT distributions as a function of difficulty, for all numbers of alternatives.

Figure 8.

Quantile-Quantile plots drawn from averaging the individual quantiles computed for each participant in Experiment 1 (represented by the dots connected to the thicker solid lines). The thinner solid lines represent x = y. Equation y = ax + b (a =slope; b =intercept) is the regression-line of y on x—slopes near the unit indicate nearly identical distributions between y and x; slopes greater than the unit show spreading of the tail in y vs. x; and slopes below the unit show spreading of the lading edge of the y distribution in comparison to x. Plots show shift in both correct and error RT distributions across difficulty levels. As number of alternatives increased RTs became slower. Very little difference in RT distribution shape was observed.

As a function of difficulty, Q-Q lines were linear but the slopes were greater than the unity— 1.08, on average—, indicating that the increase in MRT as difficulty increased was due to RT distributions spreading (see Figure 7). Q-Q plots across number of alternatives showed shifts of the entire RT distribution (while slopes did not deviate much from the mean, 0.98), for both correct and error responses, as the number of alternatives increased (i.e., RT became longer; see Figure 8). This shift was more prominent when number of alternatives increased from 2 to 3 than from 3 to 4—as measured by the average difference over the 5 quantile-RT points, approximately 45 ms and 23 ms (averaged over correct and error responses), respectively. (The individual analysis does not alter the interpretation of the group data presented above and, thus, is not shown.)

Error responses were faster than correct responses for 2 alternatives, but not for 3 or 4 alternatives. For 2 alternatives, averaging across difficulty conditions, the .9-quantile point for error responses was only about 5 ms slower than that for correct responses, whereas the .1-quantile point was about 22 ms faster. For 3 and 4 alternatives, there was almost no difference between error and correct responses in the .1-quantile point (about -5 ms and 5 ms, respectively), unlike typical two-choice results (e.g., Ratcliff and Rouder, 2000; Thapar, Ratcliff, and McKoon, 2003), whereas error responses were slower than correct responses in the .9-quantile point (by about 22 ms and by about 29 ms, respectively).

Experiment 2

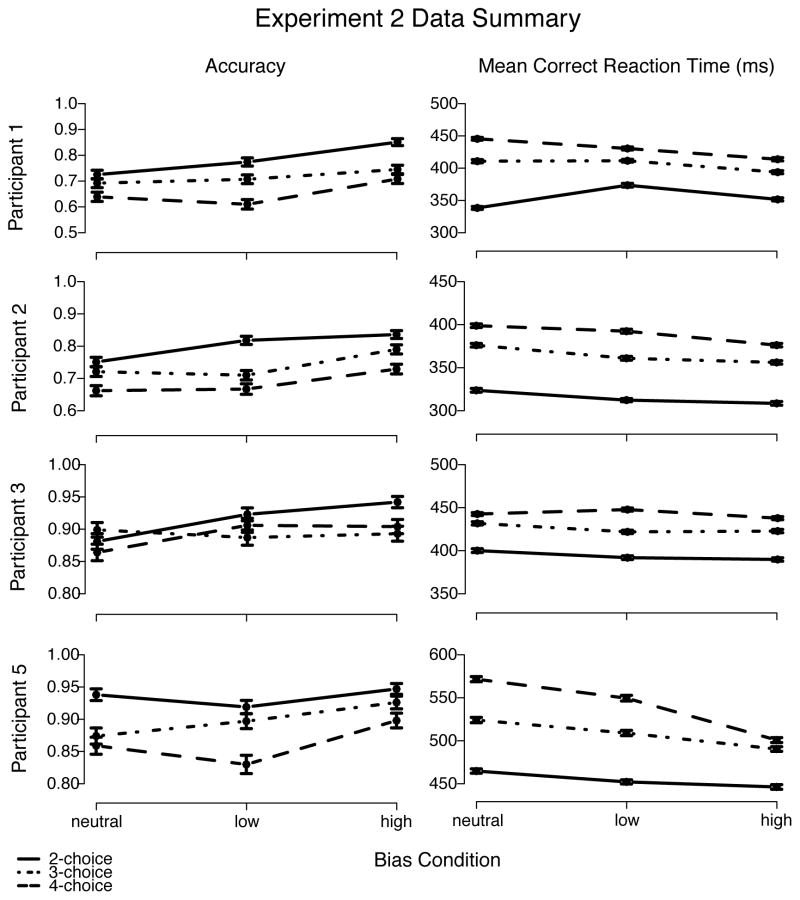
As in Experiment 1, extreme fast and slow responses were eliminated from analyses using cutoffs. Averaged over participants, in Experiment 2, the mean lower cutoffs were 213 ms, 265 ms, and 288 ms, whereas the mean upper cutoffs were 688 ms, 713 ms, and 730 ms for 2, 3, and 4 alternatives, respectively.⁴ Excluding data points in this way eliminated approximately 2.8% of the data. Overall, the results from Experiment 2 showed that mean correct RTs to high-proportion stimuli decreased and accuracy increased as blocks became more biased. Also as in Experiment 1, mean correct RT increased and accuracy decreased as number of alternatives increased (see Table 2 and Figure 9).

Table 2.

Analysis of Variance for Experiment 2

Source	df	F	η2	p
Participants	3	231.83**	.73	.00
Number of alternatives (A)	2	108.24**	.23	.00
Proportion of stimuli (P)	2	8.71*	.02	.00
A × P	4	1.16	.00	.35
Residuals	24	(145)

Note. Participants is a between-subjects factor, whereas number of alternatives and proportion of stimuli are within-subjects factors. Values enclosed in parentheses represent mean square errors.

^*p < .01.

^**p < .001.

Figure 9.

Left panel shows that accuracy decreased with increase in number of alternatives (except for Participant 3) and increased from low- to high-bias conditions. Right panel shows that mean correct RT increased with increase in number of alternatives and decreased from low-to high-bias conditions. Error bars mark one standard error below and above each point.

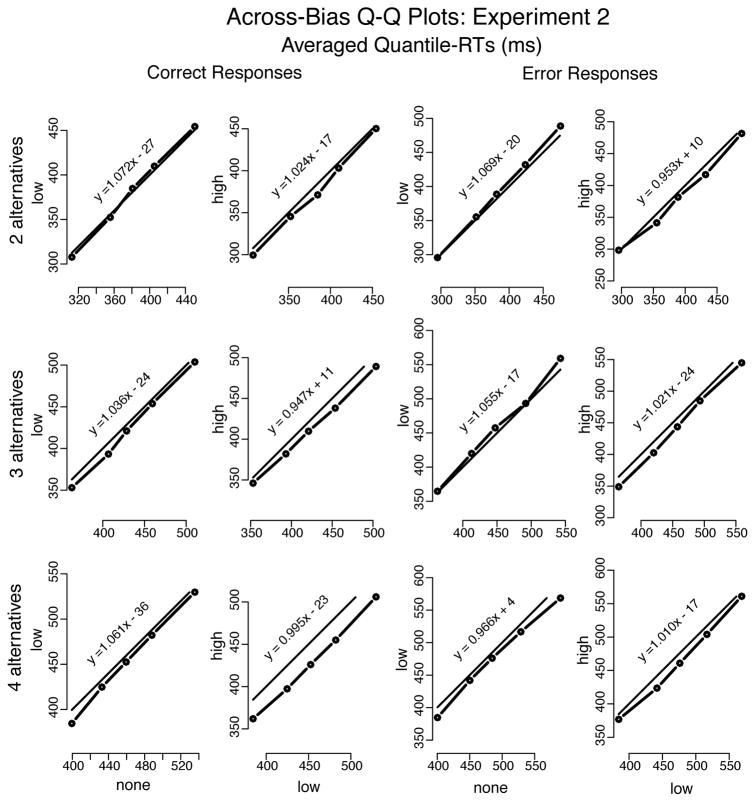
The Q-Q plots for Experiment 2 (Figure 10) were linear, as in Experiment 1, and showed little change in the shape of RT distributions as bias level increased (for both correct and error responses). They also showed a larger shift of the entire correct RT distribution when bias increased from low to high than when bias increased from none to low (approximately 15 ms and 8 ms, respectively, averaged across number of alternatives). As in Experiment 1, fast errors were present for 2 alternatives, but not for 3 or 4 alternatives.

Figure 10.

Quantile-Quantile plots drawn from averaging the individual quantiles computed for each participant in Experiment 2 (represented by the dots connected to the thicker solid lines). The thinner solid lines represent x = y. Equation y = ax + b (a =slope; b =intercept) is the regression-line of y on x—slopes near the unit indicate nearly identical distributions between y and x; slopes greater than the unit show spreading of the tail in y vs. x; and slopes below the unit show spreading of the lading edge of the y distribution in comparison to x. Nearly identical RT distributions were observed across bias conditions for 2 alternatives, but faster correct RT distributions were observed in the high-bias condition than in the low-bias condition for 4 alternatives.

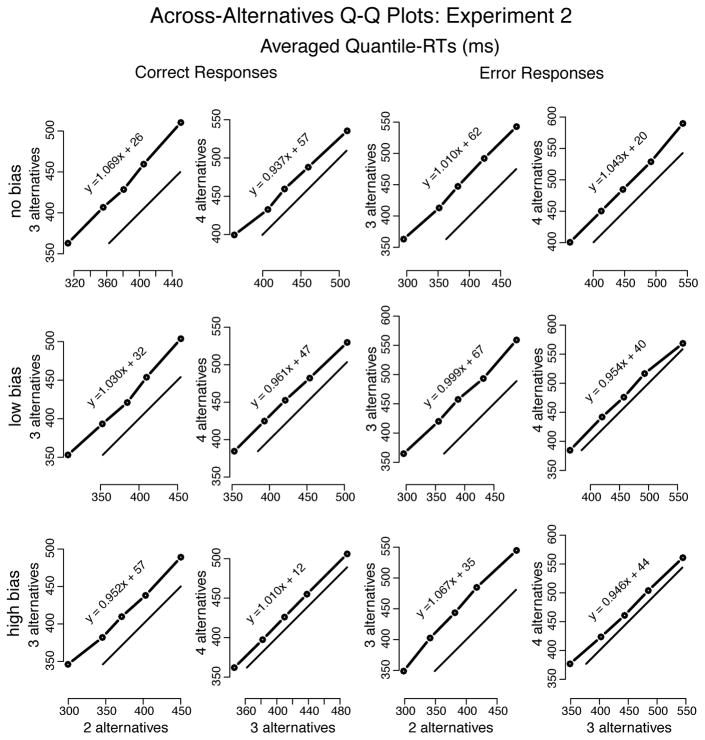
Q-Q plots of no bias vs. low bias and low bias vs. high bias (Figure 11) showed a shift of the entire RT distribution, for both correct and error responses, as the number of alternatives increased and RT became longer. This shift was less prominent when number of alternatives increased from 3 to 4 than from 2 to 3 (respectively, approximately 26 ms and 55 ms, averaged over correct and error responses). Regardless of the magnitude of the shift in RT distributions, there was little change in their shapes. In short, the increase of both bias and number of alternatives simply shifted the RT distributions.

Figure 11.

Quantile-Quantile plots drawn from averaging the individual quantiles computed for each participant in Experiment 2 (represented by the dots connected to the thicker solid lines). The thinner solid lines represent x = y. Equation y = ax + b (a =slope; b =intercept) is the regression-line of y on x—slopes near the unit indicate nearly identical distributions between y and x; slopes greater than the unit show spreading of the tail in y vs. x; and slopes below the unit show spreading of the lading edge of the y distribution in comparison to x. Dots above x = y show longer RTs for higher number of alternatives.

Modeling Analysis

There were 384 possible models from the combinations of the characteristics we presented earlier. To reduce this number to a more manageable number, we took two steps: first, by simulation, we evaluated the impact of each model parameter on the model’s predictions (even though these simulations are susceptible to parameter interaction effects); and second, we performed preliminary tests with the data from Experiment 1. Based on the first step, we find the following:

1. Decay. As decay increases, accuracy increases and spread of RT distributions increases, accompanied by slight increase in leading edge, and these changes are stronger for larger values of decay.

2. Inhibition. Small increases in inhibition cause an increase in accuracy and an increase in spread with negligible changes in the leading edge of RT distributions. When inhibition was high, change in the spread of the RT distribution was small for 2-choice conditions but larger for 3- and 4-choice conditions.

3. Decay and inhibition. When decay and inhibition have the same nonzero value (i.e., are balanced), almost identical leading edges are observed in the RT distributions, when compared to zero values of decay and inhibition. Nonzero values of decay and inhibition also lead to RT distributions with slightly larger spread than that obtained with zero values of decay and inhibition.

4. Starting point. Adding relatively small amounts of variability to starting points (i.e., 1/8 or 1/4 of the range from 0 to threshold) led to slight leftward shifts of the RT distributions. For negatively correlated starting points, a slight decrease in accuracy was observed, whereas no clear pattern was observed for random starting points.

5. Negative evidence vs. non-negative only evidence. Negatively unbounded accumulation of evidence led to an increase in accuracy and a slight increase in the spread of the RT distributions, when compared to non-negative only accumulation.

6. Number of nondecisional components. When nondecisional components are ordered such that nondecisional time for 2 alternatives is faster than for 3 alternatives, which in turn is faster than for 4 alternatives, reducing the number of nondecisional components from 3 to 1 (estimated in between the time for 2 and 3 alternatives) caused a rightward shift in the 2-choice RT distributions and a leftward shift in the 3- and 4-choice distributions.

7. Decision criterion. By itself, increasing the number of decision criteria from 1 (identical criteria for 2, 3, and 4 alternatives) to 3 (different criteria for 2, 3, and 4 alternatives) causes changes in both accuracy and RT distributions that are not readily interpretable unless the three criteria are ordered such that the criterion threshold for 2 alternatives is lower than for 3 alternatives, which in turn is lower than for 4 alternatives. When that holds, accuracy will decrease and RT distributions will have a slightly larger spread as number of alternatives increases.

8. Input strength. Having three or twelve input-strength parameters with “average” values did not allow the models to capture changes in difficulty conditions. The advantage of having twelve parameters—the preferred structure to fit our data—over three was the ability to model the accumulation of each letter alternative individually. Having thirty six input-strength parameters also allowed small changes in RT distributions and accuracy to be modeled as a function of specific letters, but such model’s BIC values were much higher than the BIC values for alternative models due to the number of parameters.

9. Decision criterion, input-strength, and decay. We also note that increasing the value of decision criterion, reducing the input-strength value, or increasing decay leads to similar slowing of RT distributions.

We were able to rule out several models because they neither qualitatively fit the data from Experiment 1 nor their Bayesian Information Criterion (BIC) values were competitive.

1. Models with inhibition. We found that the extra parameter representing mutual lateral inhibition worsened the BIC estimates without producing qualitatively better fits relative to the models that did not have such inhibition.

2. Models with non-correlated, non-identical starting points. We found that models with identical or negatively correlated starting points produced competitive BIC estimates, but models with random starting points produced higher BIC estimates.

3. Models that allowed negative evidence. These models produced poorer qualitative fits than the models with non-negative evidence only.

4. Models with 3 (target/foil, across number of alternatives) or 12 (one for each of the 4 letters, across number of alternatives) input-strength parameters. These models assumed that the experimental difficulty manipulations would be absorbed by parameters other than the input-strength parameters.

5. Models with 36 (one for each of the 4 letters, across number of alternatives and difficulty conditions) input-strength parameters. These variants did not produce competitive BIC estimates due to the much larger number of parameters than the models with 9 input-strength parameters (target/foil, across number of alternatives and difficulty conditions). Because our choice of letter alternatives was designed to use a set of letters that produced about the same confusability (cf. Gilmore et al., 1979), the exclusion of these models (which modeled accumulation rates for each specific letter separately) does not result in loss of generality.

Excluding these least competitive classes of models reduced the number of model variants to 16, involving the following differences: 3 vs. 1 nondecisional component; 3 vs. 1 decision criterion; decaying vs. non-decaying accumulation; and identical vs. different starting points (we used negatively correlated starting points for data in Experiment 1 and biased starting points for data in Experiment 2; in the latter case, target starting points will be closer to criterion threshold than the starting points of competing accumulators in the same proportion as the response alternative bias). Table 3 lists the structure of all models tested. Note that all leaky accumulator (LA) variants use non-competing racing processes with decay, which are dual diffusion models, as presented in Ratcliff et al. (2007).

Table 3.

Structure of Models Tested—The 8 models without decay shown below are structurally analogous to the 8 models with decay (not shown)

Model	Evidence	St. pt.	Decay	Inh.	ter	Criterion
	(constraints)				(parameters)
A(1T,1C,eS)	≥0	=	no	no	1	1
A(1T,1C,cS|bS)	≥0	cor	no	no	1	1
A(1T,3C,eS)	≥0	=	no	no	1	3
A(1T,3C,cS|bS)	≥0	cor	no	no	1	3
A(3T,1C,eS)	≥0	=	no	no	3	1
A(3T,1C,cS|bS)	≥0	cor	no	no	3	1
A(3T,3C,eS)	≥0	=	no	no	3	3
A(3T,3C,cS|bS)	≥0	cor	no	no	3	3

Note. St. pt. = Starting point; Inh. = Inhibition; t_er = nondecision time; cor = negatively correlated. Model variant labels abbreviate the models’ structure: A = accumulator (without decay); T = t_er; C = criterion; cS = correlated starting point (Experiment 1 only); bS = biased starting point (Experiment 2 only); eS = equal starting point. The other 8 models tested are identified by LA, meaning leaky accumulator (with decay), otherwise with the same structures.

Model Fitting

We pooled each participant’s data across sessions, provided that the session-by-session data showed relatively stable performance, as measured by MRT and accuracy. Specifically, data from initial sessions up to session i were removed from analyses if data from session i + 1 were faster by more than 10% on average or more accurate by more than .1 percentage point in any condition.

RT data were separated into error and correct RTs, and error- and correct-RT distributions were approximated by 5 quantiles, evenly spaced between .1 and .9. Each model was simultaneously fit to error- and correct-RT distributions from each individual participant. Goodness-of-fit measures were computed for each model and for each participant.

As in the preliminary tests, the main statistic we used in the minimization routines to adjust the models’ parameters in search of the best fit was BIC. We checked parameter estimates obtained from minimization with BIC against parameter estimates obtained from minimization with chi-square (χ²) and verified that these estimates were consistent. Hence, interpretation of parameter estimates of any model was not BIC-specific. We used BIC to evaluate how well the models fit the data because we needed to compare non-nested models with different numbers of parameters, a situation for which χ² ranking is inadequate. In addition, comparing models using their BIC estimates can be done in a statistically meaningful and simple way, as described by Raftery (1995).

BIC provides a penalty for the number of parameters in a model, and it penalizes models for complexity of their functional form (cf. Schwarz, 1978; Wasserman, 2000). Since our minimization routine was based on 5 quantile-RTs for correct responses and 5 for error responses, creating 6 data bins for each case, the BIC statistic is defined by

$$\mathit{BIC}=-2(\sum _{i}N{p}_{i}ln({\pi }_i))+\mathit{Mln}(N),$$ (4)

where p_i and π_i are the proportions of observed and predicted data in the ith bin, N is the number of observations in the condition, and M is the number of free parameters in the model.

The models were fit to data using the SIMPLEX fitting method (Nelder and Mead, 1965). Because there is no known explicit solution for Eq. 3, predictions from the models were obtained by simulation. We used Monte Carlo methods that generated 20,000 simulations of the decision process to compute the probabilities of the responses and their respective RT distributions. In the fitting method, each 20,000 simulations represented one iteration. The first iteration was based on a set of starting parameters, and the iterations that followed were based on the SIMPLEX adjustments to that set of starting parameters. The last iteration in a (fitting) run produced an optimal set of parameters, based on the minimum BIC (or chi-square) value obtained. In an attempt to avoid local minima, we used 3 starting-parameter sets, each of which was used to start a different serial chain of 4 SIMPLEX fits (in which each optimal set of parameters produced by a run was used as the starting set of parameters for the proceeding run; cf. Ratcliff and Tuerlinckx, 2002). The minimum BIC value among the values produced by these 3 chains is the value we report.

Best-Fitting Models

Sixteen models were fitted to the data from both Experiment 1 and Experiment 2. Table 4 shows the BIC values and their respective rankings for Experiment 1, data in the difficulty manipulation. Ties were awarded between BIC values that did not differ by more than 10 points, thus one model was only ranked over another if there was very strong support (p > .99) for that model, according to Raftery (1995, Table 6).

Table 4.

Bayesian Information Criterion (BIC) Rankings for Experiment 1

Model	Participant 1 BIC:Rk	Participant 2 BIC:Rk	Participant 3 BIC:Rk	Participant 4 BIC:Rk
A(1T,1C,eS)	42.311:14	41.272:14	40.574:14	37.277:2
A(1T,1C,cS)	41.133:11	40.772:13	40.011:11	37.401:6
A(1T,3C,eS)	40.938:6	40.150:4	39.684:5	37.535:12
A(1T,3C,cS)	41.022:8	40.252:7	39.776:7	37.523:11
A(3T,1C,eS)	40.669:1	39.945:1	39.420:1	37.304:4
A(3T,1C,cS)	40.772:2	40.042:2	39.530:2	37.417:7
A(3T,3C,eS)	40.887:4	40.165:5	39.689:5	37.397:5
A(3T,3C,cS)	41.165:12	40.472:11	40.155:13	37.725:16
LA(1T,1C,eS)	42.958:16	41.609:16	40.838:15	37.694:15
LA(1T,1C,cS)	42.618:15	41.424:15	40.899:16	37.675:14
LA(1T,3C,eS)	41.110:9	40.273:8	39.820:9	37.453:9
LA(1T,3C,cS)	41.228:13	40.478:11	40.034:12	37.578:13
LA(3T,1C,eS)	40.784:3	40.060:3	39.557:3	37.248:1
LA(3T,1C,cS)	40.877:4	40.175:5	39.655:4	37.291:3
LA(3T,3C,eS)	41.007:7	40.297:9	39.775:7	37.435:8
LA(3T,3C,cS)	41.102:9	40.416:10	39.881:10	37.509:10

Note. Model variant labels abbreviate the models’ structure: A = accumulator (without decay); LA = leaky accumulator (with decay); T = t_er; C = criterion; cS = correlated starting point; eS = equal starting point. Rk = Ranking. Ties indicate one model did not have very strong support over the other (i.e., p > .99; see Raftery, 1995, Table 6).

Table 6.

Mean Parameter Estimates for the Three Best-Fitting Models in Experiment 1

Model	$T_{er}^2$	$T_{er}^3$	$T_{er}^4$	st	decay	c2	c3	c4	σ
A(3T; 1C; eS)	0.305	0.345	0.366	0.098	0	0.972	0.972	0.972	0.459
LA(3T; 1C; eS)	0.318	0.360	0.381	0.093	0.387	0.725	0.725	0.725	0.429
A(3T; 3C; eS)	0.325	0.354	0.364	0.106	0	0.815	0.899	0.980	0.455

	${\rho }_e^2$	${\rho }_m^2$	${\rho }_d^2$	${\rho }_e^3$	${\rho }_m^3$	${\rho }_d^3$	${\rho }_e^4$	${\rho }_m^4$	${\rho }_d^4$
A(3T; 1C; eS)	.863	.774	.678	.894	.765	.596	.935	.749	.584
LA(3T; 1C; eS)	.883	.783	.673	.917	.787	.607	.938	.769	.600
A(3T; 3C; eS)	.917	.796	.689	.922	.782	.604	.926	.765	.592

Note. Average of the parameter estimates across all 4 participants. $T_{er}^n$ = nondecision time (in s) for the corresponding n number of alternatives; s_t = range of variability in t_er; cⁿ = criterion for the corresponding n number of alternatives; σ = SD in Gaussian noise added to the accumulation process; ${\rho }_{\lambda }^n$ = input strength at the λ level of difficulty (e = easy; m = medium; d = difficult) for the corresponding n number of alternatives. Model variant labels abbreviate the models’ structure: A = accumulator (without decay); LA = leaky accumulator (with decay); T = t_er; C = criterion; eS = equal starting point.

Inspection of Table 4 shows that models with both 1 nondecisional component and 1 decision criterion were consistently outranked by most other models, so we eliminated models of these two types from contention. Among the 12 remaining models, models with negatively correlated starting points were consistently outranked by models with identical starting points. Thus, we were left with 6 competitive models to explain data from Experiment 1, among which the main differences were number of parameters modeling the nondecisional component (3 vs. 1) and decision criterion (3 vs. 1).

To make sure our selection of the best-fitting model(s) would not be specific to the goodness of fit measure we used (viz., BIC), we refit these models to participants’ data by means of a corrected Akaike Information Criterion (AIC; cf. Hurvich and Tsai, 1989, AIC_c). Our AIC statistic was defined by the following equation, which corresponds to Akaike’s original description (e.g., Akaike, 1974) plus a bias-adjustment term.

$$\mathit{AIC}=-2(\sum _{i}N{p}_{i}ln({\pi }_i))+2M+2M(M+1)/(N-M-1),$$ (5)

where p_i and π_i are the proportions of observed and predicted data in the ith bin, N is the number of observations in the condition, and M is the number of free parameters in the model.

Parenthetically, we note that, unlike BIC estimates, AIC estimates yield no ties in ranking between two models. That is, if a model produces a lower AIC estimate than another model, the former is deemed statistically superior to the latter regardless of the magnitude of the difference (e.g., Akaike, 1974). Table 5 shows the ranking of the 6 remaining models according to both BIC and AIC. Inspection of that table shows agreement between BIC and AIC for the 2 best-fitting models for all 4 participants, and for the 3 best-fitting models for participants 1 and 3. Based on this agreement, we proceed to examine the fits of the 3 best-fitting models in Experiment 1, A(3T, 1C, eS), LA(3T, 1C, eS), and A(3T, 3C, eS).

Table 5.

Bayesian Information Criterion (BIC) vs. Akaike Information Criterion (AIC) Rankings of the 6 Best-Fitting Models in Experiment 1

	BIC:Rk	AIC:Rk	BIC:Rk	AIC:Rk
Model	Participant 1		Participant 2
A(1T,3C,eS)	40.938:4	39.591:5	40.150:3	38.832:5
A(3T,1C,eS)	40.669:1	39.322:1	39.945:1	38.627:1
A(3T,3C,eS)	40.887:3	39.360:3	40.165:4	38.671:3
LA(1T,3C,eS)	41.110:6	39.674:6	40.273:5	38.867:6
LA(3T,1C,eS)	40.784:2	39.347:2	40.110:2	38.654:2
LA(3T,3C,eS)	41.007:5	39.391:4	40.323:6	38.716:4

	Participant 3		Participant 4
A(1T,3C,eS)	39.684:3	38.386:5	37.535:6	36.266:6
A(3T,1C,eS)	39.420:1	38.121:1	37.304:2	35.896:2
A(3T,3C,eS)	39.689:3	38.218:3	37.397:3	35.959:4
LA(1T,3C,eS)	39.820:6	38.435:6	37.453:5	36.100:5
LA(3T,1C,eS)	39.557:2	38.173:2	37.248:1	35.895:1
LA(3T,3C,eS)	39.775:5	38.218:4	37.435:4	35.914:3

Note. Model variant labels abbreviate the models’ structure: A = accumulator (without decay); LA = leaky accumulator (with decay); T = t_er; C = criterion; cS = correlated starting point; eS = equal starting point. Rk = Ranking. A tie (in BIC rankings) indicates one model did not have very strong support over the other (i.e., p > .99; see Raftery, 1995, Table 6).

Table 6 shows mean parameter estimates for the 3 best-fitting models. Inspection of that table shows that, for all 3 of these models, (a) the change in T_er was much larger going from 2 to 3 alternatives than from 3 to 4 alternatives, and that (b) input-strength estimates decreased with increased difficulty level. The T_er increases across number of alternatives were almost half as large for model A(3T, 3C, eS) than for the two other models (both with only 1 decision criterion parameter). Specifically, from 2 to 3 alternatives, there was about a 30- vs. 40-ms increase; from 3 to 4 alternatives, there was about a 10- vs. 20-ms increase. Both magnitudes of increase are nearly linear with the logarithm of number of alternatives, and so is the increase in criterion threshold estimates for model A(3T, 3C, eS). In comparison, mean parameter estimates for competitive models with only one nondecisional parameter (e.g., A(1T, 3C, eS) in Table 7) also show that input-strength estimates decreased with increased difficulty level and that the increase in threshold criterion is nearly linear with the logarithm of number of alternatives.

Table 7.

Mean Parameter Estimates for the Two Best-Fitting 1T-Models in Experiment 1

Model		Ter		st	decay	c2	c3	c4	σ
A(1T; 3C; eS)		0.356		0.124	0	0.577	0.870	1.004	0.433
LA(1T; 3C; eS)		0.353		0.114	0.175	0.579	0.841	0.967	0.460

	${\rho }_e^2$	${\rho }_m^2$	${\rho }_d^2$	${\rho }_e^3$	${\rho }_m^3$	${\rho }_d^3$	${\rho }_e^4$	${\rho }_m^4$	${\rho }_d^4$
A(1T; 3C; eS)	.976	.826	.702	.881	.773	.610	.875	.718	.554
LA(1T; 3C; eS)	.974	.859	.724	.920	.795	.615	.905	.763	.602

Note. Average of the parameter estimates across all 4 participants. T_er = nondecision time (in s) for any number of alternatives; s_t = range of variability in t_er; cⁿ = criterion for the corresponding n number of alternatives; σ = SD in Gaussian noise added to the accumulation process; ${\rho }_{\lambda }^n$ = input strength at the λ level of difficulty (e = easy; m = medium; d = difficult) for the corresponding n number of alternatives. Model variant labels abbreviate the models’ structure: A = accumulator (without decay); LA = leaky accumulator (with decay); T = t_er; C = criterion; eS = equal starting point.

With increase in number of alternatives, input-strength parameter estimates decreased at times and increased at other times. To check how significant these changes were, we generated 25 pseudo data sets with 2,160 data points per condition, using average parameter estimates from model A(3T, 1C, eS), and then fit model A(3T, 1C, eS) to each of these data sets (see Table 6). The standard deviation of the mean drift rate parameter estimates ranged from about 0.009 to about 0.015. On average, two standard deviations from the mean equaled approximately 0.023. Hence, differences between drift rates that were greater than 0.045 were deemed significant differences. Across number of alternatives, the only significant differences were observed across all 3 models is the decrease in drift rate estimates going from 2 to 3 alternatives in the difficulty condition. In addition, for model A(3T, 3C, eS), the increase in criterion estimates across number of alternatives is also nearly logarithmic.

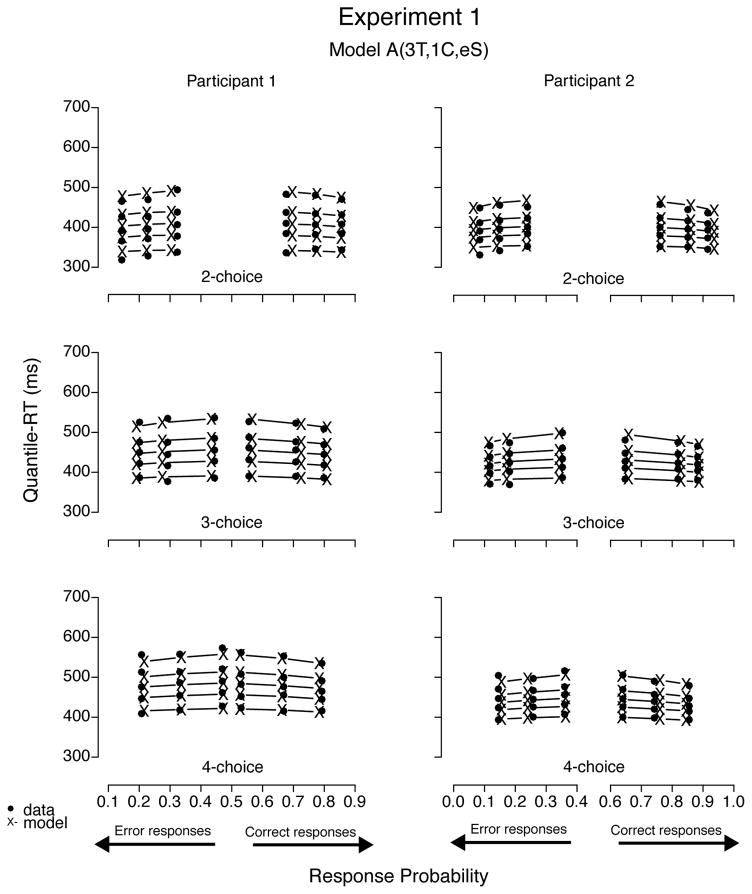
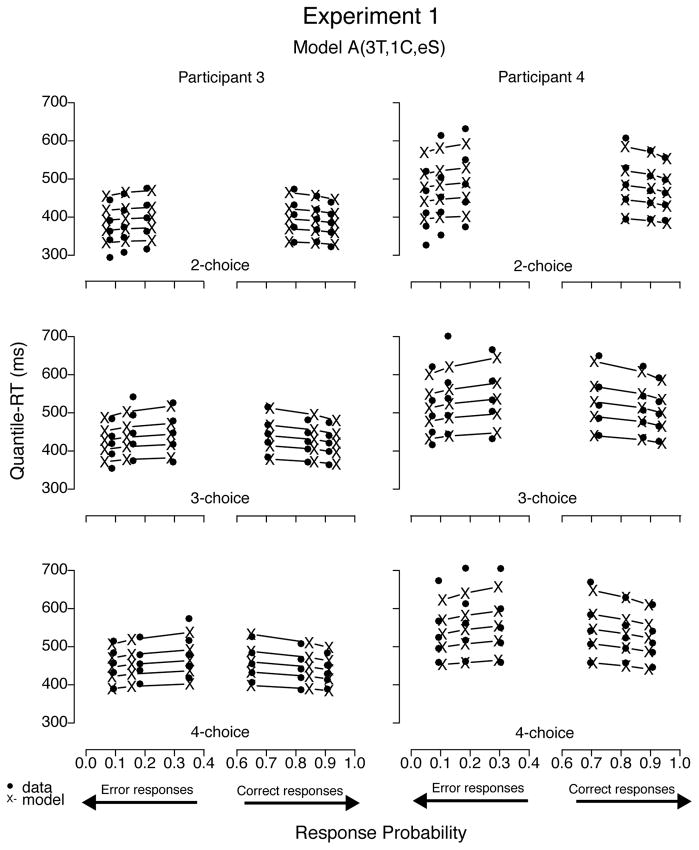
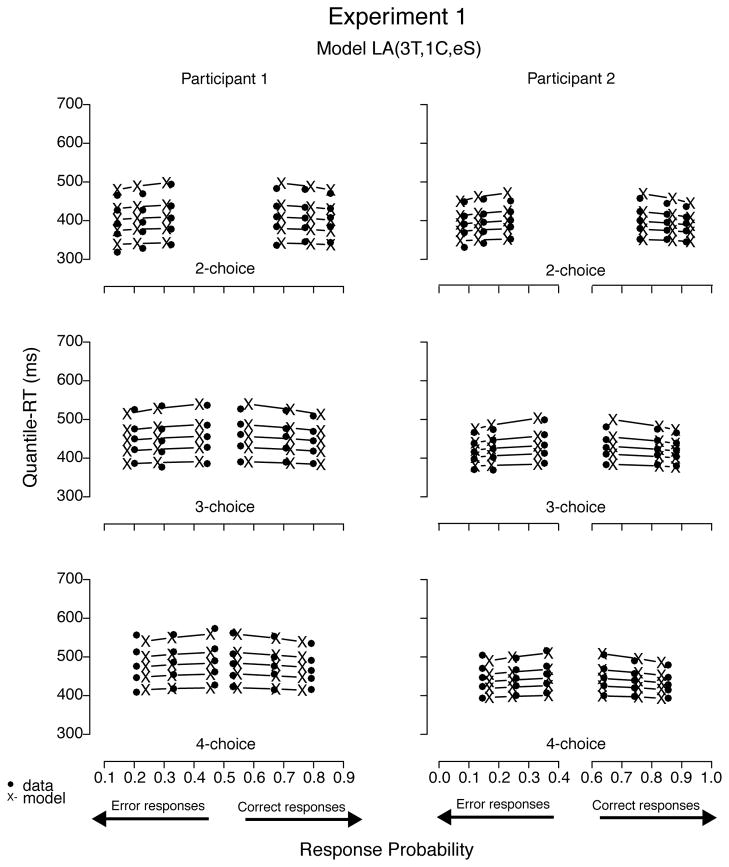
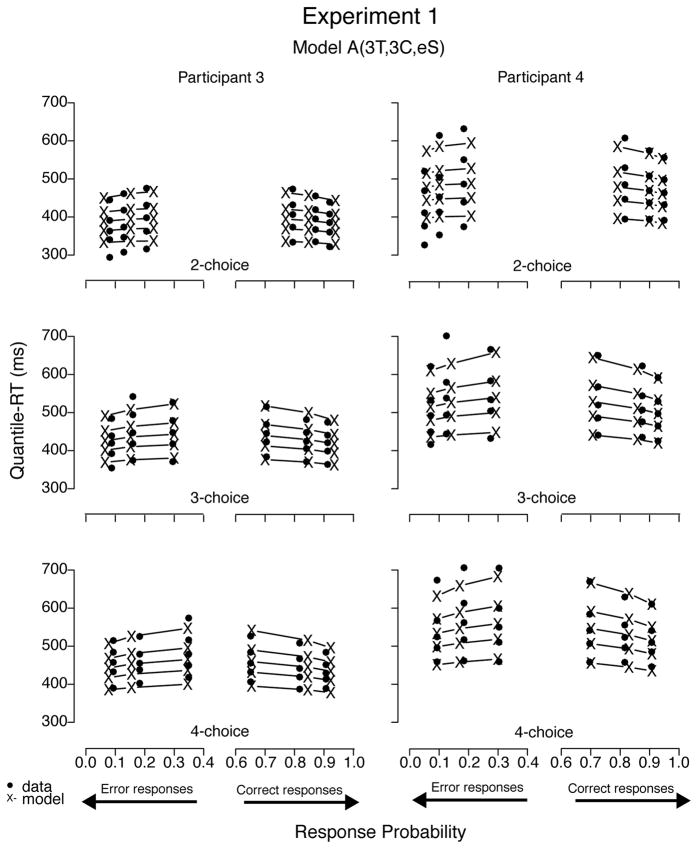
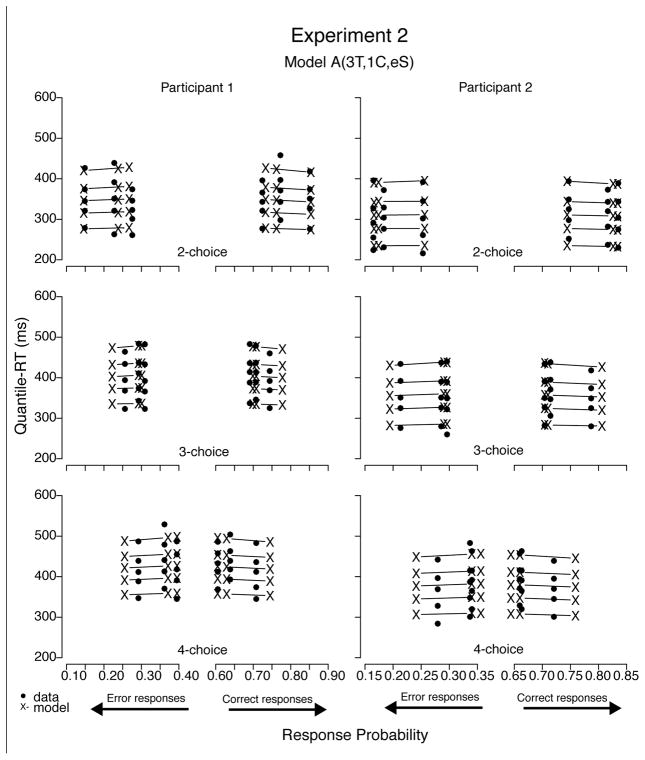
To illustrate the fits, we plotted the data sets of all four participants with predictions—using BIC parameter estimates—from model A(3T, 1C, eS), the best-fitting model for Participants 1 through 3 (see Figures 12 and 13). Predictions of all three best-fitting models were very similar; hence figures plotting their predictions were not easily distinguishable by visual inspection. Models with a decay parameter, for example, produced nearly as good fits as those without it, with decision criterion estimates 10% to 30% lower than models with no decay (cf. Table 6). In addition, the two models with one nondecisional parameter (i.e., A(1T, 3C, eS) and LA(1T, 3C, eS)) produced visually similar prediction plots as well, despite their slightly worse (quantitative) fit results. To illustrate mimicking among best-fitting models, we plotted data from Participants 1 and 2 with predictions from model LA(3T, 1C, eS) in Figure 14 and from Participants 3 and 4 with prediction from model A(3T, 3C, eS) in Figure 15. Moreover, we believe we cannot decide among competitive models that have the ability to mimic one another based on goodness of fit alone because small differences in data may rank order them differently.

Figure 12.

Quantile-Probability plots for data from Participants 1 and 2 and predictions from the best-fitting model in Experiment 1. RT points are plotted in quantile ascending order, from .1 to .9. From left to right, the 3 columns across error responses represent easy, medium, and difficult stimuli, followed by difficult, medium, and easy data points across correct responses. Model variant label abbreviates the model’s structure: A = accumulator (without decay); T = t_er; C = criterion; eS = equal starting point.

Figure 13.

Quantile-Probability plots for data from Participants 3 and 4 and predictions from the best-fitting model in Experiment 1. RT points are plotted in quantile ascending order, from .1 to .9. From left to right, the 3 columns across error responses represent easy, medium, and difficult stimuli, followed by difficult, medium, and easy data points across correct responses. Model variant label abbreviates the model’s structure: A = accumulator (without decay); T = t_er; C = criterion; eS = equal starting point.

Figure 14.

Quantile-Probability plots for data from Participants 1 and 2 and predictions from the second best-fitting model in Experiment 1. RT points are plotted in quantile ascending order, from .1 to .9. From left to right, the 3 columns across error responses represent easy, medium, and difficult stimuli, followed by difficult, medium, and easy data points across correct responses. Model variant label abbreviates the model’s structure: LA = leaky accumulator (with decay); T = t_er; C = criterion; eS = equal starting point.

Figure 15.

Quantile-Probability plots for data from Participants 3 and 4 and predictions from the third best-fitting model in Experiment 1. RT points are plotted in quantile ascending order, from .1 to .9. From left to right, the 3 columns across error responses represent easy, medium, and difficult stimuli, followed by difficult, medium, and easy data points across correct responses. Model variant label abbreviates the model’s structure: A = accumulator (without decay); T = t_er; C = criterion; eS = equal starting point.

Table 8 shows the BIC values and their respective rankings for Experiment 2, the proportion manipulation. Inspection of that table shows individual differences: the models that best fit Participant 5’s data were different from those that best fit the data of Participants 1 through 3. Specifically, the competitive models for the first three participants were models with 3 non-decisional parameters and 1 criterion parameter, whereas Participant 5’s data were better fit by models with 1 nondecisional parameter and 1 criterion parameter. For all participants, models with equal starting points outranked models with biased starting points. Parenthetically, we did not repeat model analyses with AIC because doing so in Experiment 1 did not alter the selection of the best-fitting models.

Table 8.

Bayesian Information Criterion (BIC) Rankings for Experiment 2

Model	Participant 1 BIC:Rk	Participant 2 BIC:Rk	Participant 3 BIC:Rk	Participant 5 BIC:Rk
A(1T,1C,eS)	31.882:7	41.750:15	29.217:15	28.655:1
A(1T,1C,bS)	31.764:4	40.262:3	28.942:10	28.857:3
A(1T,3C,eS)	31.900:8	40.378:6	28.788:6	29.090:11
A(1T,3C,bS)	32.002:11	40.428:8	28.897:8	29.169:14
A(3T,1C,eS)	31.640:1	40.201:1	28.568:1	28.991:7
A(3T,1C,bS)	31.712:2	40.240:2	28.700:3	29.146:12
A(3T,3C,eS)	31.853:6	40.408:7	28.753:4	29.443:16
A(3T,3C,bS)	31.910:8	40.468:9	28.921:9	29.395:15
LA(1T,1C,eS)	33.048:16	41.850:16	29.389:16	28.792:2
LA(1T,1C,bS)	32.299:15	40.720:14	29.197:14	28.856:3
LA(1T,3C,eS)	32.137:13	40.583:12	28.972:12	28.853:3
LA(1T,3C,bS)	32.200:14	40.659:13	29.050:13	29.050:9
LA(3T,1C,eS)	31.736:3	40.300:4	28.647:2	28.884:6
LA(3T,1C,bS)	31.790:5	40.348:5	28.774:5	29.050:9
LA(3T,3C,eS)	31.931:10	40.510:10	28.849:7	29.001:7
LA(3T,3C,bS)	31.997:11	40.554:11	28.961:11	29.145:12

Note. Model variant labels abbreviate the models’ structure: A = accumulator (without decay); LA = leaky accumulator (with decay); T = t_er; C = criterion; bS = biased starting point; eS = equal starting point. Rk = Ranking. Ties indicate one model did not have very strong support over the other (i.e., p > .99; see Raftery, 1995, Table 6).

The best-fitting model was model A(3T, 1C, eS) for Participants 1 through 3 and model A(1T, 1C, eS) for Participant 5. Input-strength estimates did not differ significantly between neutral and low-bias conditions, but they significantly increased with increase in level of bias for the target response between low- and high- bias conditions (see Table 9; for a comparison with low- vs. high-frequency targets, see Appendix). Because the main manipulation in Experiment 2 involved proportion of stimuli, it may be expected that evidence parameters (i.e., input strength) do not change and that decision parameters (i.e., decision criterion) do. We could have constrained all the models that way. Rather, we decided to let the fits confirm or disconfirm this expectation, allowing both decision and input-strength parameters to change across level of bias in some models (e.g., model LA(1T, 3C, eS)). If input-strength parameters were estimated to be about the same values, this would allow us to constrain them to be equal. Instead, we found that decision criterion parameter estimates did not differ much when allowed to vary across bias conditions, whereas input-strength estimates differed.

Table 9.

Individual Parameter Estimates for the Best-Fitting Models in Experiment 2

P	Model	$T_{er}^2$	$T_{er}^3$	$T_{er}^4$	st	decay	c2	c3	c4	σ
1	A(3T; 1C; eS)	0.269	0.329	0.352	0.138	0	0.723	0.723	0.723	0.496
2	A(3T; 1C; eS)	0.228	0.280	0.306	0.150	0	0.785	0.785	0.785	0.534
3	A(3T; 1C; eS)	0.300	0.335	0.358	0.106	0	0.747	0.747	0.747	0.352
M	A(3T; 1C; eS)	0.266	0.315	0.339	0.131	0	0.752	0.752	0.752	0.461
5	A(1T; 1C; eS)	0.285	0.285	0.285	0.178	0	1.246	1.246	1.246	0.235

P		${\rho }_n^2$	${\rho }_l^2$	${\rho }_h^2$	${\rho }_n^3$	${\rho }_l^3$	${\rho }_h^3$	${\rho }_n^4$	${\rho }_l^4$	${\rho }_h^4$
1	A(3T; 1C; eS)	.738	.703	.867	.738	.750	.857	.688	.718	.899
2	A(3T; 1C; eS)	.730	.839	.850	.767	.778	.938	.774	.794	.968
3	A(3T; 1C; eS)	.745	.802	.839	.758	.793	.808	.785	.832	.892
M	A(3T; 1C; eS)	.738	.781	.852	.754	.774	.868	.749	.781	.920
5	A(1T; 1C; eS)	.672	.658	.726	.513	.525	.576	.418	.433	.524

Note. Individual parameter estimates for best-fitting model, according to BIC. Column labels match that of Table 6, except for: ${\rho }_{\lambda }^n$ = input strength at the λ level of bias (n = neutral; l = low; h = high) for the corresponding n number of alternatives. P = Participant number; M = Mean for participants 1 through 3.

This increase in target input-strength estimates when target frequency is higher than distractor frequency can be interpreted as a shift in “drift criterion” (Gomez et al., 2007; Ratcliff, 1985; Ratcliff et al., 1999). This shift can be psychologically interpreted as a shift on the input-strength dimension analogous to a change in criterion in signal detection theory (see Ratcliff and McKoon, 2008, Figure 3). In our case, there was a small shift in drift criterion from no bias to low bias and a larger shift from low bias to high bias. Addition of alternatives, on average, did not cause significant changes in input-strength estimates for model A(3T, 1C, eS), but caused a decrease in all bias conditions for model A(1T, 1C, eS).

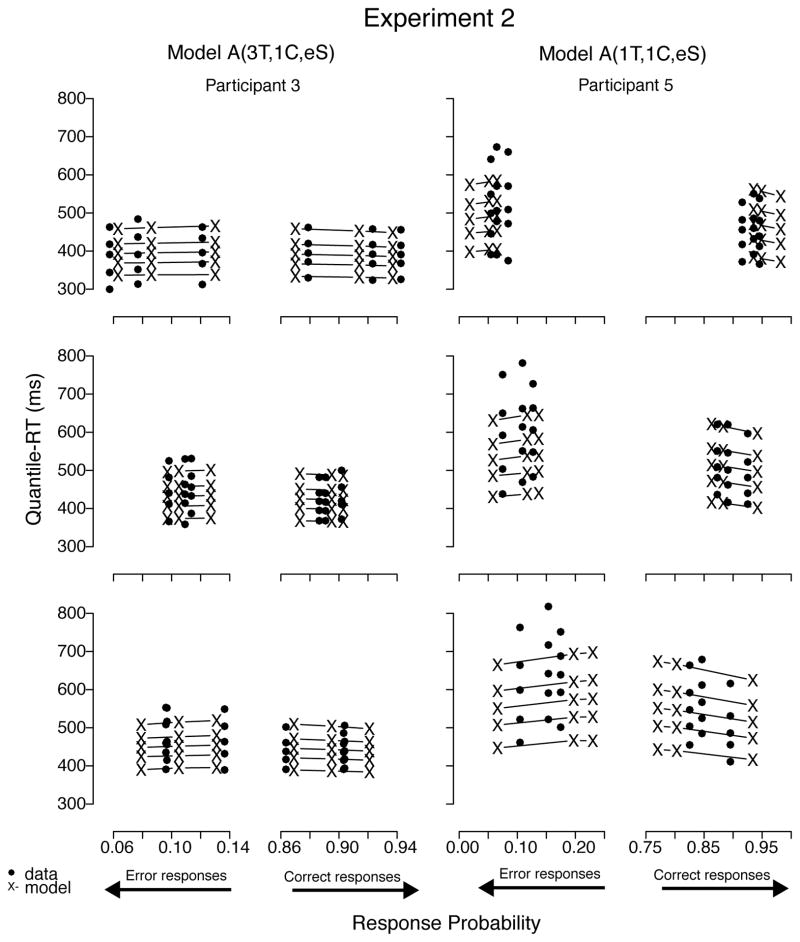
Figures 16 and 17 illustrate the fits with plots of the data sets of all four participants with predictions from their respective best-fitting models (i.e., either A(3T, 1C, eS) or A(1T, 1C, eS)). As was the case in Experiment 1, predictions of all four best-fitting models were very similar and, hence, their predictions were not easily distinguishable by visual inspection only. Models with decay (e.g., values around 0.5) produced similar fits to those without decay, with criterion estimates about 15% lower.

Figure 16.

Quantile-Probability plots for data from Participants 1 and 2 and predictions from the respective best-fitting model in Experiment 2. RT points are plotted in quantile ascending order, from .1 to .9. From left to right, the 3 columns across error responses represent high-, low-, and no-bias conditions, followed by no-, low-, and high-bias data points across correct responses. Model variant label abbreviates the model’s structure: A = accumulator (without decay); T = t_er; C = criterion; eS = equal starting point.

Figure 17.

Quantile-Probability plots for data from Participants 3 and 5 and predictions from the respective best-fitting model in Experiment 2. RT points are plotted in quantile ascending order, from .1 to .9. From left to right, the 3 columns across error responses represent high-, low-, and no-bias conditions, followed by no-, low-, and high-bias data points across correct responses. Model variant label abbreviates the model’s structure: A = accumulator (without decay); T = t_er; C = criterion; eS = equal starting point.

Discussion

In this article, we explore perceptual decision in a multiple-alternative experimental paradigm. Our aim was to examine a range of architectural features that a model could contain and attempt to determine which were needed to fit experimental data well. Several families of decision models were applied to the data from two experiments using a multiple-alternative letter discrimination task. The models assume racing diffusion processes and represent the decision process as a stochastic accumulation of evidence toward decision criteria. Statistical analysis of model fits allowed several model families to be eliminated.

The models that produce good fits for both experiments all share the following characteristics. First, the models use nine input-strength parameters, one for each level of difficulty crossed with the number of alternatives. Each of the nine parameters is for a target drift rate. The other (foil) drift rates are determined by the appropriate target drift rate because target and foil drift rates sum to the unit and foil drift rates are assumed to be equal. This allows the model to account for both the addition of alternatives and either an increase in difficulty (Experiment 1) or an increase in target-stimulus proportion (Experiment 2). Second, accumulation of evidence is bounded to be non-negative. Third, the models do not need lateral inhibition between accumulators. Fourth, the models do not need leakage in the accumulators.

For Experiment 1, the best-fitting models account for data with either three nondecisional parameters or three decision criteria (or both), one for each difficulty level. For Experiment 2, the best-fitting models have either one or three nondecisional parameters, but they need only one decision criterion parameter with the same value for each accumulator for two, three, and four alternatives.

In both experiments, the quality of fits for the best-fitting models cannot be discriminated by eye. These best-fitting models are all capable of fitting correct RT distributions well, but all miss the relatively short leading edges for error RT distributions obtained with two alternatives in both experiments. This mimicking among competitive models is well known (e.g., Ashby and Townsend, 1980), and perhaps the best way to address the problem within this class of models would be to apply the models to a wider range of data and experimental paradigms (such as tasks with deadlines or response signal procedures), as suggested previously by Ratcliff (1988b).

The main architectural differences among the three best-fitting models for the perceptual difficulty manipulation involve the decay and the number of decision criterion parameters as a function of the number of alternatives. Models with a decay parameter mimic the performance of models with no decay by reducing the value of the criteria. Models with three decision criterion parameters perform like models with one criterion, with slight adjustments to the values of the criteria and also to the nondecisional component. Model analyses also show that among the three best-fitting models, irrespective of model architecture, input-strength significantly decreases with the increase in number of alternatives from two to three, but only in the difficult condition. This suggests that the addition of alternatives is more disruptive when the quality of evidence is poor, and that the amount of disruption that one extra alternative causes gets gradually smaller as the size of the set of alternatives gets larger.

We find that the nondecisional component of processing increases with increase in number of alternatives. An (ad-hoc) interpretation is that addition of alternatives increases the preparation time to respond.⁵ The magnitude of the increase in nondecition time estimates for models with one criterion parameter, however, makes this interpretation implausible, but estimates from models with three decision criteria are consistent with it. For the latter models, parameter estimates also indicate that individuals become more cautious as the number of alternatives grows larger, and the nature of this increase in decision criteria is nearly logarithmic. This is equivalent to Hick’s law (cf. Eq. 1) applied to a component of processing (as opposed to a measure of performance).

Our modeling analyses seem to lead to a conundrum. Should we select the best-fitting model strictly on numerical grounds or may we reject the best numerical choice in favor of a model with an almost equivalent qualitative fit? For example, we prefer a model that has only one nondecisional component as a function of number of alternatives, rather than three, in order to provide an account that is more consistent with what we know about encoding and motor response subprocesses.⁶

Model analyses of data from Experiment 2 (which manipulated frequency of target stimulus) indicate that, like in Experiment 1, the nondecisional component of processing increases with increase in number of alternatives. Unlike Experiment 1, participants used the same decision criterion for two, three, and four alternatives. Both experiments give insights into how slight changes in accuracy across number of alternatives are explained: they are natural predictions of these types of models, caused by the redistribution of weight from one to two distractor accumulators and from two to three distractor accumulators.

In summary, we describe perceptual decision based on the stochastic accumulation of evidence toward a criterion. We find that several families of racing diffusion process models, differing only by a few assumptions—at times only a single assumption—can be discriminated when fitted to the same multiple-alternative data sets. Some can be eliminated outright on the bases of statistical comparison among goodness-of-fit values. In the class of successful models, the models do not need lateral inhibition or decay in order to fit multiple-alternative data well. Furthermore, we find variability in the duration of encoding and response output subprocesses and within-trial noise to play an important role in the processing of evidence.

Some more general issues raised by this study are as follows. First, these are data from just one kind of experimental paradigm. It could be that the winning models are specific to this and similar paradigms, or it could be that these winning models apply over the whole range of appropriate tasks.

Second, it may seem easy to find an experimental paradigm that allows comparisons across number of alternatives. However, this is more difficult than it seems. There are problems in making sure that stimuli are equally difficult across number of alternatives, as well as making sure that reasonable ranges of accuracy and RTs are produced. A major issue for many choices of tasks is that participants might be able to adopt a strategy of, for example, first making a decision about choices A and B, then considering C. Such strategies would result in a different class of model architectures.

Third, it may seem easy to generalize decision models from two-choice to multiple-alternative paradigms (e.g., Audley and Pike, 1965, Figure 1; Bogacz et al., 2007; LaBerge, 1962; Laming, 1968, Figures 3.4 and 6.1; Usher and McClelland, 2001). However, as we have noted above, there is a large number of possible assumptions that can be made about the architecture and component processes of models, and this can lead to a large family of models to evaluate.

Fourth, this strategy of competitive model testing allowed us to reduce the number of competitive modeling assumptions in the perceptual decision task we used. We suggest that this approach could be more generally useful in discriminating among families of models in other multiple-alternative paradigms (e.g., recognition memory discussed in Ratcliff and Starns, 2009) in order to arrive at the most competitive models in those paradigms.

The research we report focuses on examining theoretical descriptions of perceptual decision making that are capable of being extended from two-choice paradigms to multiple-alternative paradigms. The successful models describe the decision as a race toward a criterion driven by the accumulation of sensory evidence over time. In that dynamic accumulation of sensory evidence, we find that neither lateral inhibition between alternatives nor decay in evidence are necessary decision making among multiple alternatives. This study also provides a case study in evaluating candidate perceptual decision making models.

Appendix

Low- vs. High-frequency Targets

As an anonymous reviewer pointed out, a more curious reader might wonder whether a model analysis that pitched low-frequency vs. high-frequency targets could provide extra information. We do not present such analysis in the main text because the conditions with low-frequency targets (in low- or high-bias conditions) have considerably fewer data points than responses to high-frequency targets. Thus, modeling results for low-frequency targets alone might not be as meaningful as we would like them to be.

In the main text, we report results from an aggregate analysis, considering both low- and high-frequency target responses, which, because of the discrepancy in the number of data points we highlight above, are dominated by the high-frequency responses. We foresaw that the magnitude of the effects might be amplified should we report only on the basis of high-frequency targets, for example, but we avoided that option so not to bias our analysis. Nevertheless, Tables A1 and A2 are included here to serve as an illustration of how input-strength and criterion parameters might change across the frequency of the target and how much the parameter estimates might change from the aggregate to the specific. (To produce Tables A1 and A2, we used the best-fitting models shown in Table 9 so that a comparison is straightforward.)

Table A1.

Individual Parameter Estimates in Experiment 2: High-frequency

P	Model	$T_{er}^2$	$T_{er}^3$	$T_{er}^4$	st	decay	c2	c3	c4	σ
1	A(3T; 1C; eS)	0.265	0.323	0.351	0.133	0	0.726	0.726	0.726	0.456
2	A(3T; 1C; eS)	0.235	0.283	0.311	0.138	0	0.687	0.687	0.687	0.427
3	A(3T; 1C; eS)	0.298	0.334	0.352	0.106	0	0.744	0.744	0.744	0.328
M	A(3T; 1C; eS)	0.266	0.313	0.338	0.126	0	0.719	0.719	0.719	0.404
5	A(1T; 1C; eS)	0.329	0.329	0.329	0.272	0	1.048	1.048	1.048	0.162

P		${\rho }_n^2$	${\rho }_l^2$	${\rho }_h^2$	${\rho }_n^3$	${\rho }_l^3$	${\rho }_h^3$	${\rho }_n^4$	${\rho }_l^4$	${\rho }_h^4$
1	A(3T; 1C; eS)	.701	.761	.904	.671	.772	.894	.643	.756	.960
2	A(3T; 1C; eS)	.675	.856	.869	.680	.803	.924	.667	.713	.955
3	A(3T; 1C; eS)	.723	.779	.817	.743	.782	.808	.746	.853	.852
M	A(3T; 1C; eS)	.700	.799	.863	.698	.786	.875	.685	.774	.922
5	A(1T; 1C; eS)	.747	.773	.876	.571	.643	.771	.501	.576	.736

Note. Individual parameter estimates for high-frequency targets. Column labels match that of Table 6, except for: ${\rho }_{\lambda }^n$ = input strength at the λ level of bias (n = neutral; l = low; h = high) for the corresponding n number of alternatives. P = Participant number; M = Mean for participants 1 through 3.

Table A2.

Individual Parameter Estimates in Experiment 2: Low-frequency

P	Model	$T_{er}^2$	$T_{er}^3$	$T_{er}^4$	st	decay	c2	c3	c4	σ
1	A(3T; 1C; eS)	0.265	0.336	0.368	0.139	0	0.811	0.811	0.811	0.639
2	A(3T; 1C; eS)	0.240	0.294	0.329	0.148	0	0.743	0.743	0.743	0.588
3	A(3T; 1C; eS)	0.303	0.342	0.361	0.112	0	0.758	0.758	0.758	0.371
M	A(3T; 1C; eS)	0.269	0.324	0.353	0.133	0	0.771	0.771	0.771	0.533
5	A(1T; 1C; eS)	0.353	0.353	0.353	0.254	0	0.974	0.974	0.974	0.153

P		${\rho }_n^2$	${\rho }_l^2$	${\rho }_h^2$	${\rho }_n^3$	${\rho }_l^3$	${\rho }_h^3$	${\rho }_n^4$	${\rho }_l^4$	${\rho }_h^4$
1	A(3T; 1C; eS)	.818	.523	.626	.857	.793	.793	.860	.810	.807
2	A(3T; 1C; eS)	.771	.748	.605	.866	.774	.755	.886	.901	.778
3	A(3T; 1C; eS)	.772	.863	.859	.819	.863	.767	.827	.781	.839
M	A(3T; 1C; eS)	.787	.711	.697	.847	.810	.772	.858	.831	.808
5	A(1T; 1C; eS)	.788	.718	.659	.588	.581	.545	.511	.489	.518

Note. Individual parameter estimates for high-frequency targets. Column labels match that of Table 6, except for: ${\rho }_{\lambda }^n$ = input strength at the λ level of bias (n = neutral; l = low; h = high) for the corresponding n number of alternatives. P = Participant number; M = Mean for participants 1 through 3.

Taking the means row of Table A1 and comparing it to the means row of Table 9, we note that the decision criterion is about 96% of the overall estimate among high-frequency targets and that the increase in input-strength estimates is more prominent across all bias levels. Both observations are consistent with the participants’ expectations of the high-frequency targets: psychologically, expected targets might need to accumulate less evidence before a decision in their favor is made (although this difference is not quantitatively significant in our case); and the more a target is expected, the larger its strength to elicit an identification response.

Inspecting Table A2 the same way and comparing its means row to the means row of Table 9, we note that the decision criterion is about 3% higher than the overall estimate and that input-strength estimates show a decreasing trend with increase in bias toward other targets (essentially biasing participants against these low-frequency targets). These observations are again consistent with participants’ expectations of the high-frequency targets: more evidence might be required of targets that appear infrequently than of targets that appear frequently (although again it is the case that this difference is not quantitatively significant); and the less a target is expected, the smaller its strength to elicit an identification response. Together, these two tables confirm the top-down influence on the perceptual task caused by the expectation of the stimulus, which is opposite in nature to the bottom-up influence caused by the perceptual difficulty manipulation of Experiment 1.