Anticipatory Control of Motion-to-Force Transitions With the Fingertips Adapts Optimally to Task Difficulty

Abstract

Moving our fingertips toward objects to produce well-directed forces immediately upon contact is fundamental to dexterous manipulation. This apparently simple motion-to-force transition in fact involves a time-critical, predictive switch in control strategy. Given that dexterous manipulation must accommodate multiple mechanical conditions, we investigated whether and how this transition adapts to task difficulty. Eight adults (19–39 yr) produced ramps of isometric vertical fingertip force against a rigid surface immediately following a tapping motion. By changing target surface friction and size, we defined an easier (sandpaper, 11 mm diam) versus a more difficult (polished steel, 5 mm diam) task. As in prior work, we assembled fine-wire electromyograms from all seven muscles of the index finger into a seven-dimensional vector defining the full muscle coordination pattern—and quantified its temporal evolution as its alignment with a reference coordination pattern vector for steady-state force production. As predicted by numerical optimizations to neuromuscular delays, our empirical and sigmoidal nonlinear regression analyses show that the coordination pattern transitions begin sooner for the more difficult tasks than for the easier tasks (∼120 ms, P < 0.02, and ∼115 ms, P < 0.015, respectively) and that the coordination pattern transition in alignment is well represented by a sigmoidal trend (R^2 > 0.7 in most cases). Importantly, the force vector following contact had smaller directional error (P < 0.02) for the more difficult task even though the transition in coordination pattern was less stereotypical and uniform than for the easier task. These adaptations of transition strategy to task difficulty are compatible with an optimization to counteract neuromuscular delays and noise to enable this fundamental element of dexterous manipulation.

INTRODUCTION

Dexterous manipulation often requires us to rapidly make contact with objects to produce well-directed fingertip force vectors. For example, quickly grasping small, round, or fragile objects like wine glasses, beads, berries, etc. all involve transitioning abruptly from moving the fingertip toward a rigid surface to producing a well-directed fingertip force vector against it. From a mechanical perspective, this commonplace task is extremely challenging because the control for accurate finger motion is incompatible with that for well-directed static force. Several authors (e.g., Hogan 1985; Venkadesan and Valero-Cuevas 2008; Whitney 1987) have demonstrated that this switch in control strategy is unavoidably sensitive to time delays and errors in planning. In biological systems, this control challenge is exacerbated by the inability of the neuromuscular system to switch control strategies and muscle contractions instantaneously or exactly.

Recently we showed that the human nervous system performs this abrupt switch in control strategy via an anticipatory, time-critical, and neurally demanding transition of muscle activations before contact (i.e., from those controlling finger motion to those controlling fingertip force) (Venkadesan and Valero-Cuevas 2008). In addition to ruling out a passive impedance based strategy to mediate the contact with the surface, we found that the muscle coordination pattern clearly transitions from that for motion to that for isometric force ca. 65 ms before contact. We then used mathematical modeling and analysis to reveal a switch in the underlying control strategy. Importantly, time delays due to muscle activation-contraction dynamics suffice to impose a physical limit on directional accuracy of the fingertip force vector on contact.

Subsequent numerical simulations (Venkadesan and Valero-Cuevas 2009) show that an anticipatory transition in joint torques (analogous to that seen experimentally for muscle activations) is a necessary control strategy to reach the physical limits of the directional accuracy of force production on contact. This anticipatory strategy arises in our deterministic model as a means to compensate for neuromuscular time delays and not from optimizing for robustness to noise/uncertainties. Importantly the model also shows that advancing the onset of the transition in joint torques is an optimal response to increased task difficulty (e.g., small, round, and fragile objects that are wet vs. dry or rough vs. slippery).

Given the stringent mechanical requirements of the motion-to-force transition, the delays and noise of the neuromuscular system, and the predicted temporal modulation with task difficulty, we hypothesized that the nervous system will adapt the onset of the transition of muscle coordination patterns to task difficulty. We defined the difficulty of the motion-to-force transition by the size and coefficient of friction of the target surface as either “easier” (rough-large: a high friction, larger-diameter target) or “more difficult” (smooth-small: a low friction, smaller-diameter target).

METHODS

The experimental methods are the same as in Venkadesan and Valero-Cuevas (2008) in which complete details can be found. In this abridged description, we focus on how we varied the difficulty of the task by changing the coefficient of friction and size of the target surface and on the novel analysis methods.

Experiment

The task consisted of ramping up a fingertip force to a self-selected high magnitude (∼100% maximal voluntary contraction (MVC)) against a flat horizontal target surface after approaching the surface with a downward motion (Fig. 1 A). That is, subjects performed an abrupt transition from the production of downward motion with their fingertip toward the target surface followed by the production of a large downward static force. Subjects tapped the horizontal surface of two cylindrical pedestals: “smooth” (polished steel) and “small” (5 mm diam) versus “rough” (360-grit sandpaper) and “large” (11 mm diam). The pedestal was mounted on a six-axis load cell (model 20E12A-I25, JR3, Woodland, CA) with a force resolution of 0.01 N. Subjects wore a custom-molded thermoplastic (MaxD, North Coast Medical, Morgan Hill, CA) thimble with a spherical 4.8-mm-diam Teflon bead embedded on its distal aspect. This thimble rigorously defined the mechanical task via a unique contact point and friction cone for force direction (Valero-Cuevas et al. 1998, 2000; Venkadesan and Valero-Cuevas 2008). The task was performed by eight consenting right-handed individuals (average age: 22.8 yr, range: 19–39 yr) with no history of neurological or hand pathology or injury. They all read and signed a consent form for this protocol approved by Cornell University's Committee on Human Subjects.

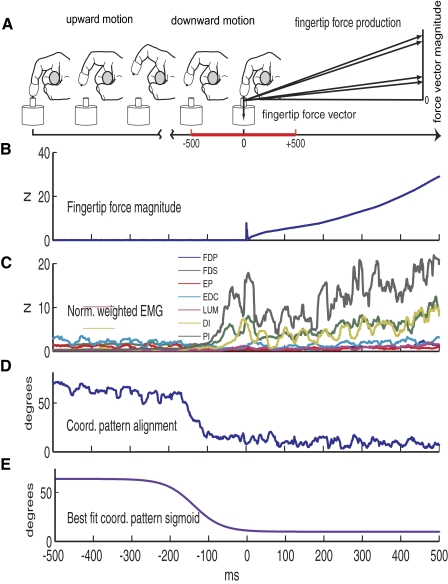
Fig. 1.

Description of experiment. A: description of the task: following 4 brief preparatory taps over a specified target, the subject executed a last tap where after making contact with the target, the subject ramped up the vertical force applied by his finger to a maximum. The figure shows this last tap. The time of interest was 500 ms before and after contact (red in the time axis). The subject is wearing a custom thimble during the taps; the thimble allowed a unique contact point and friction cone for force direction. B: fingertip force in the 3 directions was recorded while performing the task; the figure shows the vertical force magnitude for 1 trial 500 ms before and after contact. C: fine-wire EMG from the 7 muscles of the index finger was recorded while performing the task. Normalized weighted electromyograph (EMG) is obtained after being filtered, full-wave rectified, normalized (by maximal voluntary contraction), weighted (by physiological cross-sectional areas), and smoothed (50-ms symmetric moving average) the EMG signals. D: the norm weighted EMG for each of the muscles, constitute a component of the muscle coordination pattern 7-dimensional (7D) vector [m(t)]. The coordination pattern alignment is the angle between the m(t) for each interval of time (−500 to 500 ms) and the m(t) at the time when the vertical force reached its maximum value. E: the best fit that described the evolution of the coordination pattern alignment during the transition from motion to force is a sigmoid.

Two sessions were run on separate days. In the first session, the experimental setup was adjusted to the dimensions of the subject's hand, and the subject became acquainted with and practiced the task. In the second session, fingertip force in the three directions and fine-wire electromyograms (EMGs) were recorded (2,000 sample/s) from all muscles of the index finger while performing the task. Fine-wire intramuscular electrodes were placed in the seven muscles of the index finger using previously reported techniques (Valero-Cuevas et al. 1998; Valero-Cuevas 2000; Venkadesan and Valero-Cuevas 2008). The muscles of the index finger are: flexor digitorum profundus (FDP), flexor digitorum superficialis (FDS), extensor indicis proprius (EI), extensor digitorum communis (EC), first lumbrical (LUM), first dorsal interosseous (DI), and first palmar interosseous (PI).

Each subject produced three trials per target surface, each of which consisted of four brief preparatory taps, followed by a tap-ramp-and-hold task (Fig. 1 only shows the last tap). We instructed the subjects to ramp-up the magnitude of the fingertip force against the surface as quickly as possible, trying the best they could to keep the finger still and the direction of the force vertical. To enable natural task performance, we did not provide direct visual feedback of force magnitude or direction. In our experience and that of others (Cole 2006), young adults are quite adept at directing forces perpendicular to the surface even in the absence of direct feedback about vector direction. Each trial was followed by a mandatory 30-s rest period to avoid fatigue. To mitigate learning effects, if any, we randomized the surface used. After the experiments were over, we reviewed the force and motion plots of each trial and discarded those where the subjects slipped while producing the force, did not produce a uniformly ascending force ramp, or prolonged their last tap and left <450 ms to complete tapping motion. The final data consisted of 30 trials, 16 using the smooth-small target and 14 using the rough-large target.

Analysis

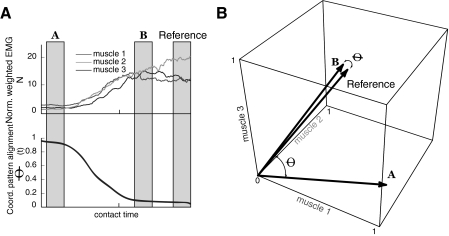
As in our prior work, we characterized the muscle coordination pattern [m(t)] as the time-varying seven-dimensional (7D) unit vector of muscle forces estimated from the filtered (band-pass: 100–1,000 Hz) and then full-wave rectified, normalized (by MVC), weighted (by physiological cross sectional areas), and smoothed (50-ms symmetric moving average) EMG signals (Fig. 1C) as in Valero-Cuevas (2000) and Venkadesan and Valero-Cuevas (2009). The temporal evolution of the coordination pattern vectors for each trial was quantified by the angle of alignment [θ(t)] of their unit vectors [m(t)] with respect to the unit vector of the reference coordination pattern (m_ref) defined during 80 ms of peak force for each trial, which occurred roughly 400 ms after contact with the surface (Venkadesan and Valero-Cuevas 2009). Figure 1D shows the evolution of the alignment of one such unit vector from −500 to +500 ms before and after contact, respectively, for a sample trial. The onset of force (t = 0) was defined at the beginning of the impact spike (Fig. 1B). We excluded the first 10 ms of data after the onset of force from our analysis because unavoidable high-frequency impact transients in the force sensor polluted the measurement of the force vector magnitude and direction. A perfect alignment θ(t) = 0 means that the relative activations among muscles are the same as m_ref, thus the same muscle coordination pattern is being used at those two time periods. Likewise, the greater the misalignment θ(t) > 0, the greater the differences in the muscle coordination patterns being used at those two time periods. Figure 2 shows a schematic vector representation of the muscle coordination pattern alignment during three different intervals (before contact, after contact, reference) for a three-dimensional muscle coordination pattern, i.e., if the system only had three muscles. From the figure, it is observed that the angle between the average unit vector during time interval B and the average unit vector during the reference interval is small compared with the angle between the average unit vectors in the A and reference intervals.

Fig. 2.

Vectorial representation of the coordination pattern. A: normalized weighted EMG signals from 3 muscles and its coordination pattern alignment during transition from motion to force. In gray we emphasize 3 specific times (A, B, reference). B: the coordination pattern vectors [m(t)] for these 3 specific times (A, B, reference). Measuring the alignment between vectors [θ(t)] allows us to make quantitative comparisons, the coordination pattern at time A is further away from the reference than the coordination pattern is at time B. The 3D space is defined by each of the muscles where the EMG signal was acquired.

We used both nonparametric (i.e., empirical) and parametric (i.e., nonlinear regression) methods to test for differences in the evolution of coordination pattern alignment across the two levels of difficulty. In this way, we guard ourselves against the possibility that apparent differences between tasks may simply reflect the fact that the nonlinear regression is a better model for one dataset than the other. As we present in the results, we find that the results from both analyses agree. For the empirical method, we plotted the mean subject data, both raw and low-pass filtered (using a 50-ms symmetrical moving average), as subjects transitioned from producing motion to producing static force in the two levels of difficulty. The second method was to perform least-squares fitting to sigmoids, or logistic regression curves, to the coordination pattern alignment data, θ(t), because sigmoids are appropriate functions to characterize the general trend for a smooth transition between two states. Our prior work shows that the nature of our angle time histories (the motor command as represented by the EMG and its analysis) indeed reveals a smooth transition between two states (Venkadesan and Valero-Cuevas 2008), Fig. 1D. Note that we do not mean to imply that the nervous system follows a sigmoidal trend in its latent command to the exclusion of other possible trends, or that the transition of the latent command signal is a sigmoid. We do mean, however, that a sigmoid is an appropriate choice when describing the simple general trend of the motor command when transitioning between two states.

We used MATLAB (Natick, MA) to fit a sigmoid of the following form to the θ(t) data

$$\widehat{\theta }\left(t\right)=\mathrm{a}\frac{1+u{e}^{-t/\tau }}{1+v{e}^{-t/\tau }}u,\nu >0$$ (1)

This characterizes the temporal transition of the relative angle between muscle coordination pattern from −500 and +500 ms with respect to the contact time. The initial angle θ between the unit vectors m(t) and m_ref is a(u/v) (i.e., the initial asymptote early in the finger movement), and a is the final angle θ between m(t) with m_ref. (i.e., final asymptote reached during steady-state static fingertip force production occurring roughly 400 ms after contact). θ̂(t) is the best fit to the θ(t) data. After fitting the sigmoid function to each trial, we normalized the sigmoid functions to have initial and final asymptotes of 1 and 0, allowing us to compare the trends in the transitions of muscle coordination pattern across subjects, trials, and levels of difficulty.

We also analyzed the magnitudes of coordination pattern vectors m(t) during the abrupt transition from motion to force, calculated as the Euclidean norm

$$\left|m\left(t\right)\right|=\sqrt{\mathrm{EM}{\mathrm{G}}_{\mathrm{FDP}}^2+\mathrm{EM}{\mathrm{G}}_{\mathrm{FES}}^2+\mathrm{EM}{G}_{\mathrm{EI}}^2+\mathrm{EM}{\mathrm{G}}_{\mathrm{EC}}^2+\mathrm{EM}{\mathrm{G}}_{\mathrm{LUM}}^2+\mathrm{EM}{\mathrm{G}}_{\mathrm{DI}}^2+\mathrm{EM}{\mathrm{G}}_{\mathrm{PI}}^2}$$ (2)

We did not fit sigmoids to these vector magnitude data because they do not asymptote within the first 500 ms after contact and thus cannot be represented as switching between two states.

The accuracy of fingertip force production on contact was quantified by the angular deviation of the force vector from the surface normal (φ(t) = 0). After low-pass filtering (80-Hz cut-off, 10th-order Butterworth digital filter) the force data, the angular deviation of the force vector, φ(t), was obtained by the negative arc tangent of the square root of the squares of the force component parallel to the sensor surface (x and y) divided by the normal component (z)

$$\varphi \left(t\right)=\arctan \left(\frac{\sqrt{f{x}^2+f{y}^2}}{\left|fz\right|}\right)$$ (3)

We performed a two-way ANOVA test with subject as a random effect to determine whether task difficulty affects the quality of the fingertip force assessed by the average φ from 10 to 500 ms and φ at 65 ms after contact.

RESULTS

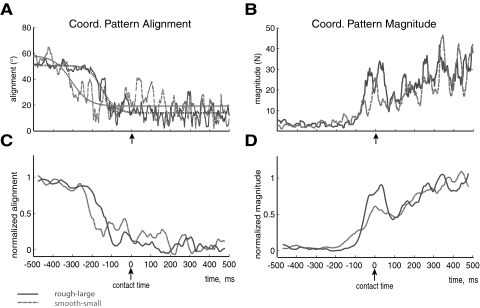
As in our prior work (Venkadesan and Valero-Cuevas 2009), transitioning between the production of motion to the production of force is accompanied by a transition in muscle coordination patterns [m(t)] as shown by changes in the alignment of the coordination pattern unit vector, θ(t). Figure 3, A and B, shows the changes in alignment and magnitude of the coordination pattern vectors for one representative trial for both task difficulties. Figure 3A also contains the best-fit sigmoids that model the alignment data. Figure 3, C and D, shows the alignment and magnitude after the data from A and B was normalized and smoothed by a 50-ms-wide moving average. Normalization was done in each trial by making the mean of the first and last 200 ms be initial and final values. The normalized θ(t) began at one and ended at zero, and the normalized force magnitudes started at zero and ended at one. Then, we compared across different trials and conditions because the empirical plots had similar start and final values. Fig. 4, A and B, shows the average alignment ± SE and average magnitude ± SE transitions (after being normalized and smoothed) from all subjects for each condition.

Fig. 3.

Coordination pattern alignment and magnitude of a representative subject. A: coordination pattern alignment and their sigmoidal fits during transition from motion to force where the surface of contact was either smooth-small (dashed) or rough-large. B: coordination pattern magnitude during transition from motion to force where the surface of contact was smooth-small (dashed) or rough-large. C: same as in A after the coordination pattern alignment was normalized and smoothed by a moving average of 50 ms. D: same as in B after the coordination pattern alignment was normalized and smoothed by a moving average of 50 ms.

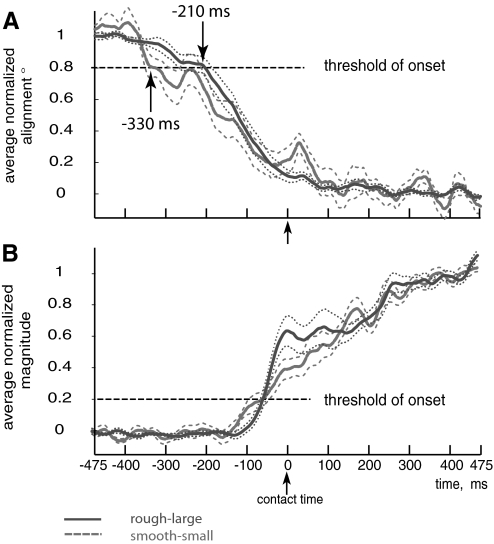
Fig. 4.

Empirical averaged coordination pattern alignment and magnitude. A: normalized, smoothed coordination pattern alignment after been averaged across all trials separated by task difficulty, i.e., smooth-small (dashed) and rough-large. The threshold of the transition onset is marked with a horizontal line at 0.8, the coordination pattern for the smooth-small case starts the transition sooner than the coordination pattern for a rough-large case (−330 vs. −210 ms, respectively). The thinner dashed lines represent the coordination pattern alignment plus or minus their standard errors for each condition. B: normalized, smoothed coordination pattern magnitude after having been averaged across all trials separated by task difficulty i.e., smooth-small (dashed) and rough-large. The threshold of the transition onset is marked with a dashed horizontal line at 0.2, the coordination pattern for smooth-small case starts the transition slightly sooner than the coordination pattern for a rough-large case.

Figures 3 and 4 show empirically that the transition of both alignment and magnitude differs across task difficulty (smooth-small or rough-large conditions). We see that switching in magnitude and alignment for the small-smooth condition occurs earlier. For the alignment, we found a significant difference in the time of onset between the two conditions (P = 0.02) with an average onset value of −330 ms for the smooth-small case and −210 ms for the rough-large case. However, interpreting these empirical trends in alignment can be of limited value because of the naturally high variability of the EMG signals. Fitting a sigmoid to each of the trials (as in Fig. 3A) is arguably a better descriptor of the transition because it captures the general trend.

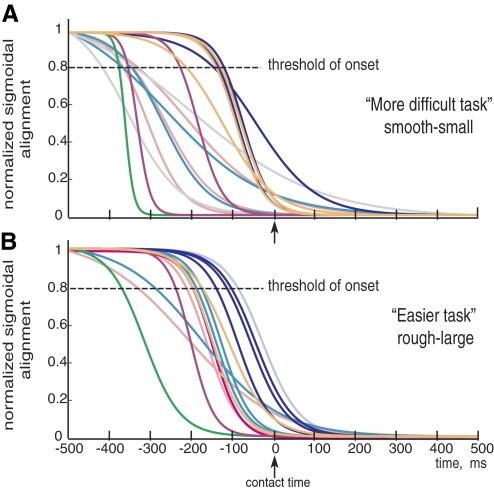
Echoing the empirical trends, we see that the majority of the sigmoids for the more difficult condition have an early onset, whereas only three sigmoids do so for the easier condition. Figure 5 shows the fitted normalized sigmoids to all alignment trials color-coded by subject: A for a rough-large surface and B for a smooth-small surface. Figure 6 shows the transition in alignment for both conditions after averaging across trials ± SE.

Fig. 5.

Individual fitted sigmoids, color-coded by subject. Normalized best-fit sigmoids for each of the trial, when the surface of contact was: smooth-small (A) or rough-large (B). We find that the transition for the easier task occurs later than for the more difficult task (except for 1 subject) in support of the reported mean values we present (Fig. 6).

Fig. 6.

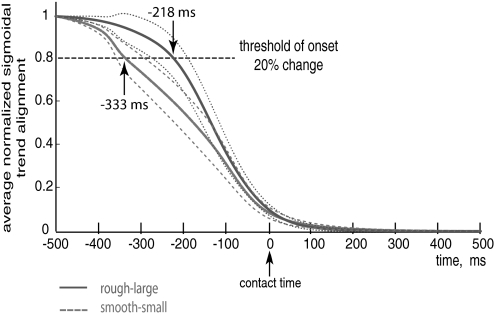
Normalized sigmoidal trend alignment. The coordination pattern alignment trend was obtained after having averaged the adjusted sigmoids from all the trials separated by task difficulty, i.e., smooth-small (dashed) and rough-large. The threshold of the transition onset is marked with a horizontal line at 0.8, the coordination pattern for the smooth-small case starts the transition sooner than the coordination pattern for the rough-large case (−333 vs. −218 ms, respectively). The thinner dashed lines represent the coordination pattern alignment trend ± SE for each condition.

Averaging the normalized trends for each condition shows that the transition in muscle coordination pattern alignment for the smooth-small case begins ∼115 ms earlier than for the rough-large case (Figs. 4A and 6). We defined the onset of the transition in coordination pattern alignment when the global mean for all cases drop 20% from the normalized value of 1 (see horizontal dashed lines in Figs. 6A and 4A), although any thresholds >10% show the same effect. Importantly, the change in muscle coordination pattern alignment is 90% complete at the time of contact for both conditions. From Fig. 6 we find that the mean onset of the transition for the smooth-small case was 333 ms and for the rough-large case was 218 ms before contact. Calculating the onset of the transition trial by trial basis and then averaging them for each condition, we obtained mean transition onset values of 273 and 220 ms, respectively, for smooth-small and rough-large. After transformation to normality (using log10), an ANOVA test was performed with subject as a random effect to evaluate if the difference between transition times of onset was significant for different conditions, we obtained P = 0.015. Without transformation to normality P = 0.019 was obtained. Thus both methods of calculating the onset find that the more difficult case has a statistically significant earlier onset.

For the transition in coordination pattern magnitude (Fig. 4B), we found that the smooth-small case begins 30 ms earlier than for the rough-large case. Recall that we did not use a regression analysis for the magnitude data.

Moreover, while the sigmoidal function fits closely the trends in the evolution of the alignment of coordination patterns for both difficulties, the sigmoidal function is nevertheless better for the easier condition. The average coefficient of determination ± SE for the least squares fit to the 30 fitted trials was R^2 = 0.79 ± 0.037. When separating the data by task difficulty, the sigmoidal model fits the rough-large case significantly better (average R^2 of 0.9 ± 0.02) than the smooth-small case (R^2 = 0.7 ± 0.06), P = 0.0008. The statistical significance of the average coefficient of determination was assessed using a two-way ANOVA test with subject as a random effect. The data were transformed $\left\{1/\left[\sqrt{-\text{In⁡(}{R}^2)}\right]\right\}$ to achieve a normal distribution to meet the assumptions of these parametric statistical tests given that correlation coefficients exhibit floor and ceiling effects. Lilliefors tests were used to evaluate normality. For completeness, we report that a P = 0.0003 was obtained without transformation to normality.

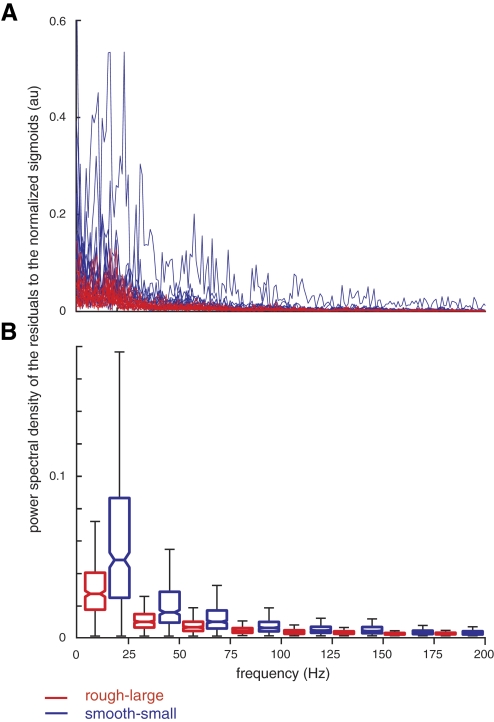
In a subsequent analysis, we also computed the power spectral density of the residuals to the sigmoidal fit (to discard the frequency spectrum of the sigmoids and account only for the variability about the sigmoidal trend). We see clear differences when we plot the power spectral density (obtained via fft) of the residuals to the normalized sigmoids (Fig. 7). This shows in a quantitative way that the nature of the variability about the sigmoidal trend differs across conditions, suggestive of more on-line regulation in the case of the more difficult task (see discussion).

Fig. 7.

Power spectral density of the residuals to the normalized sigmoids. After removing the general trend of a sigmoid, the alignment of the muscle coordination pattern shows significantly more power over a greater frequency range for the more difficult task (blue). A: fast Fourier transform from 0 to 200 Hz. B: box plots of average power in bins 25 Hz wide. Nonparametric comparison of medians ± notches (SE) quantifies that the nature of the variability about the sigmoidal trend differs across conditions for frequencies <100 Hz where power is nonnegligible.

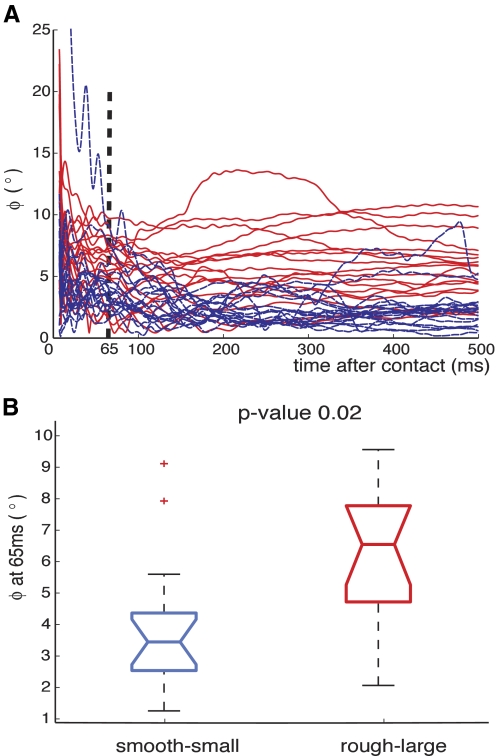
Figure 8 A shows angular deviation from vertical of the initial fingertip force vector, φ, from +10 to +500 ms after contact. The plot shows the results from all trials for each condition. A two-way ANOVA test with subject as a random effect indicated that the angular error φ at +65 ms (Fig. 8B) and the average φ from 10 to 500 ms were significantly lower for the smooth-small case P = 0.02 and P < 0.0001, respectively. Lilliefors tests showed it was necessary to transform the φ data, and we used a log10 transformation. Without transformation the P value was <0.001. We chose to analyze φ at +65 ms because it is a conservative threshold for any corrections of the force vector on the basis of sensory information at contact (see discussion).

Fig. 8.

Deviation of the fingertip force vector after contact. A: deviation angle of force vector from vertical, φ, from all trials for the 2 conditions: smooth-small (dashed, blue) and rough-large (red). The first 10 ms were excluded for all analyses. The force direction appears to deviate more for the rough-large condition than for the smooth-small condition. B: comparison of the deviation angle at 65 ms after contact between smooth-small and rough-large condition. The angle of deviation at 65 ms is significantly higher for the rough-large than for the smooth-small condition (P = 0.02).

DISCUSSION

A central limitation of the neuromuscular system is its inability to switch between control strategies instantaneously or exactly due to unavoidable excitation-contraction dynamics and noise. Therefore as described previously (Venkadesan and Valero-Cuevas 2008), the human nervous system implements an anticipatory, time-critical, and neurally demanding switch in control strategy to effectively perform the abrupt transition from the control of motion to the control of fingertip force. In addition, numerical simulations predicted that tuning the onset of the anticipatory transition to task difficulty is compatible with an optimal strategy that counteracts neuromuscular delays to reach the physical boundaries of performance (Venkadesan and Valero-Cuevas 2009). We now show experimentally that changes in task difficulty change the temporal features of muscle coordination patterns during motion-to-force transitions with the fingertips. We characterized the temporal features of these anticipatory strategies in humans and show that the adjustments in transition strategy in response to task difficulty are indeed compatible with that optimal strategy when performing this critical aspect of dexterous manipulation.

As in our prior work (Venkadesan and Valero-Cuevas 2008, 2009), we first briefly discuss the relationships of our findings to past work on anticipatory motor control, and the limitations of our approach. Multiple studies have characterized anticipatory control in the limbs of humans and animals: 1) for smooth motion-force tasks for limbs subject to contacting (e.g., manipulanda experiments) (Lackner and DiZio 2005; Shadmehr and Mussa Ivaldi 1994) and noncontacting (e.g., Coriolis force experiments) (Lackner and DiZio 2005 and references therein) force fields, 2) during abrupt postural perturbations associated with catching (Lacquaniti et al. 1992; Lacquaniti and Maioli 1989), and 3) animal studies of posture versus ground-reaction force control (Lacquaniti and Maioli 1994) or posture versus movement control (Kurtzer 2005). Our results agree with their findings and conclusions to the extent that the nervous system can and does effectively anticipate changes in task constraints. In addition, the timing of the onset of anticipatory changes in EMG of ∼200 ms prior to changes in task constraints is similar to those found previously (Lacquaniti and Maioli 1989). However, our work critically extends their and our prior work by being the first, to our knowledge, to record complete muscle coordination patterns from a musculoskeletal system (limb or finger) and full 3D force vectors to investigate whether and how the nervous system adapts the predictive transition of muscle coordination patterns to the difficulty of the task of switching abruptly from motion-to-force production. We believe the limitations of our approach do not challenge the validity of our conclusions. Although the use of a custom-molded thimble may appear unnatural, its potential drawbacks are outweighed by the benefits of a well-defined standardized contact condition across subjects (e.g., fingernail length and shape, skin dryness, friction conditions). This has allowed us to obtain high-fidelity biomechanical recordings that can be well approximated by and compared with computational models (Valero-Cuevas et al. 1998; Valero-Cuevas 2000; Venkadesan and Valero-Cuevas 2008, 2009). In addition, the use of the thimble does approximate precision pinch acquisition of small or slippery objects. The results here also suggest future studies such as the effect of lengthy practice/learning on the neural strategy or the inclusion of specialized populations such as microsurgeons or pianists.

The first type of adaptation to task difficulty we see is in the temporal advancement of the transition in coordination pattern vector. The advancement of the transition onset in the vector alignment, θ(t), of the coordination pattern for task difficulty is compatible with ideas of optimal control. Using both empirical and nonlinear regression analyses, we find that the onset of the transition for the more difficult task occurred sooner than for the easier task. The average onset value of −330 ms for the smooth-small case for the symmetrical moving average; and −210 ms for the rough-large compared with similar average onset times of −333 and −218 ms obtained from the adjusted sigmoids (Figs. 3, 4, and 6). Therefore our results and conclusions regarding the temporal advancement of the transition do not depend entirely on the assumptions of sigmoids. When analyzing the sigmoid fits on a subject-by-subject basis (color coded in Fig. 5), we find that the transition for the easier task occurs later than for the more difficult task (except for 1 subject), in support of the reported mean values we present (Fig. 6). Advancing the onset of the transition can, at the very least, improve performance in the more difficult case because it allows more time to implement the coordination pattern for the production of well-directed force against a slippery surface. More formally, our recent published computational model of motion-to-force transitions (Venkadesan and Valero-Cuevas 2009) shows that advancing the onset of the transition in joint torques is an optimal adaptation to increased task difficulty because of the unavoidable latency of muscle activation-contraction dynamics (∼36 ms) (Zajac 1989). We have also shown that in this experimental paradigm, muscle activation-contraction dynamics remains a rate-limiting process in transitioning to the muscle coordination pattern to produce well-directed isometric force on contact (Venkadesan and Valero-Cuevas 2008). Therefore this advancement of the transition of coordination pattern vector alignment and vector magnitude can be considered an optimal adaptation to task difficulty.

The fact that the change in coordination pattern vector direction precedes the change of vector magnitude in all cases is also in agreement with our prior work where we show that such temporal disparity represents a nonlinear transformation of the coordination pattern (Venkadesan and Valero-Cuevas 2009). (A linear transformation would involve simultaneous and proportional scaling of both the vector magnitude and direction.) We recently showed in computational simulations that such nonlinear transformations are a task-optimal way to compensate for neuromuscular delays and achieve accuracy of initial force direction (Venkadesan and Valero-Cuevas 2008).

The second important tuning in response to the difficulty of the task is that the transition of vector alignment, θ(t), of the coordination pattern for the easier task was more “stereotypical” than for the more difficult task, suggesting different planning and implementation of the neural control strategy (Fig. 7). We use the term stereotypical to mean that in one case (the easier task) the coordination pattern more closely follows the general trend of a sigmoid when transitioning between two states. This greater compatibility with the general trend of a sigmoid is quantified by the higher coefficients of determination. The high coefficients of determination for both task difficulties (>0.7 on average) show that the sigmoidal model fits both cases very well. That is, the change in coordination pattern vector alignment with time can be explained as the transition between asymptotes with a single inflection point. However, the significantly higher average coefficient of determination for the transitions for the easier task (0.9 ± 0.02 vs. 0.70 ± 0.06) shows that a sigmoid model is an even better model for the easier task. Conversely, the transitions for the more difficult task contain features that cannot be captured as well by a stereotypical sigmoid function. This significant difference in the smoothness of the trends in the transition of coordination pattern alignment strongly suggests that there are differences in the planning and implementation of the neural control strategy across conditions. Namely, the easier task seems to be driven predominantly by a more stereotypical feed-forward and predictive motor command that more closely follows the general trend of a sigmoid and is reminiscent of the kind that is well established in simple reach-to grasp tasks (Lukos et al. 2008 and references therein). Conversely, the departure from a simple sigmoid suggests that the more difficult task is achieved with more adjustments to the motor command. In the subsequent spectral analysis, we see that the variability about the general trend of the sigmoid in the case of the more difficult task has significantly more power over a greater frequency range. This greater complexity in the transition of coordination pattern alignment for the more difficult case is strongly indicative of more intense on-line regulation of the motor command. Given that in the motion prior to the transitions of coordination pattern alignment covers the 500 ms before contact, there is sufficient time to allow sensory-driven and internal model corrections at all sensory and cortical latencies e.g., from visuomotor to efferent-copy feedback loops (Venkadesan et al. 2007; Venkadesan and Valero- Cuevas 2009 and reference therein)—which may be upregulated to perform the adjustments we see for the more difficult task. In fact, this is an additional benefit to advancing the onset of the transition in coordination pattern alignment for the more difficult case that our computational models did not take into account. Namely, if on-line corrections are upregulated in the more difficult task, then initiating the transition sooner allows more time to complete on-line corrections in the presence of neuromuscular delays and noise. We have recently shown that such rich, task-optimal, on-line corrections are not only possible but actually present in the control of accurate fingertip forces (Valero-Cuevas et al. 2009b).

The directional accuracy of the fingertip force vector at contact provides a third line of evidence suggesting different planning and implementations of the neural control strategy with task difficulty. The misdirection of the fingertip force vector error at +65 ms (before any corrections in the force vector can be implemented on the basis of tactile sensory information at contact) (Cole and Abbs 1988; Eliasson 1995; Johansson 1992; Johansson and Birznieks 2004; Kandel et al. 2000), is significantly lower for the more difficult task (Fig. 8). That is, a less stereotypical and less smooth transition of coordination pattern alignment results in a more accurate initial force direction against the low-friction surface; whereas a more stereotypical and smoother transition of coordination pattern alignment results in a less accurate initial force direction against the high-friction surface. In short, the upregulation of the sensorimotor corrections of the transition of coordination pattern alignment has the functional consequence of improving the accuracy of the force task. This idea of on-line corrections resulting in higher EMG variability and improved performance is compatible with our prior work (Valero-Cuevas et al. 2009b). We refrain from commenting further on the details of force production beyond +65 ms after contact for several reasons. First the focus of this work is to explore the trends in muscle coordination during the motion-to-force transition, which saturates and is 90% complete before contact. Second, as stated in the preceding text, any changes in force magnitude and direction beyond +65 ms can be attributed to a large number of possible voluntary and involuntary mechanisms—and are thus best studied under specifically designed conditions as in, for example, (Valero-Cuevas et al. 1998, 2009b).

How can we interpret this upregulation in the context of control theory and neuromuscular control? We specifically mean that the more difficult task (smooth-small) displays greater on-line corrections (i.e., departure from the sigmoidal trend and variability at higher frequencies) in response to variability and disturbances arising from the constraints of the task and noise in the nervous system. We explicitly designed our experiment around two different short-duration tapping tasks, one with tighter constraints on motion and force accuracy than the other. Therefore optimal control theory would require that the nervous system precompute (i.e., learn) control laws and gains tuned to each task (for a review of control theory in the context of neuromuscular control, please see Valero-Cuevas et al. 2009a). Importantly, for noisy systems such as the sensorimotor system, there is a trade-off between accuracy and sensitivity to noise because tasks that require higher accuracy need to reject perturbations more aggressively. This is exactly what we see in our results. Performing the task with tighter constraints (i.e., on the final position of the fingertip and accuracy of the initial fingertip force) will naturally exhibit more variability than the task with more relaxed constraints because the perturbation-rejection gains need to be higher. In fact, our results provide new critical evidence at the level of muscle commands of real consequences of endogenous noise to sensorimotor control of movement.

Equally importantly, these results showing effective on-line corrections critically modify the common view that grasp acquisition is universally a memory-driven, feed-forward phenomenon (Lukos et al. 2008 and references therein). Surely the predictive nature of grasp acquisition is undeniable as seen by the onset of the transition in muscle coordination patterns prior to fingertip contact—and which in other work is seen as preshaping of the fingertips and predictable grip forces (Lukos et al. 2008). However, our results reveal a previously unseen layer of low-level control at the level of muscle coordination: the upregulation of on-line corrections to the motor command underlying the predictive trend. These results are compatible with, and add to the significance of, early reports of kinematic adjustments during rapid finger motions (Cole and Abbs 1986). The specific mechanisms for these on-line corrections remain unclear, however, so future work is called for.

This work also allows us to articulate clear paths to improve our understanding of the neural control of dexterous manipulation. For example, the main features of this anticipatory strategy can be explained by deterministic models (Venkadesan and Valero-Cuevas 2008, 2009) as an optimal adaptation to neuromuscular time delays with no need to consider optimizing for robustness to noise/uncertainties. However, our findings indicating greater variability in the motor command for the more difficult task compel us to consider the extent to which upregulation of on-line corrections are indeed driven by a need to establish robustness to noise/uncertainties. In addition, our results oblige us to develop computational models and experimental paradigms to systematically interrogate the nervous system to identify the specific sensory and/or feedback and/or efference copy mechanisms responsible for the context-dependent up-regulation of on-line corrections used to improve performance—and more rigorously establish whether and how optimality principles apply to the control of fingertip forces to enable dexterous manipulation. Last, future work is needed to expand the current thinking attributing grasp acquisition to purely feed-forward processes to establish a context-dependent continuum of control strategies. In summary, on the basis of our results and our prior work, we conclude that these three adaptations to task difficulty are all compatible with an optimal strategy to counteract neuromuscular delays to enable this fundamental feature of dexterous manipulation: making rapid contact with the object to produce well-directed forces.

GRANTS

This material is based on work supported by the Whitaker Foundation, National Science Foundation Grants 0312271 and 0237258, and National Institute on Aging AR-050520 and AR-052345 to F. J. Valero-Cuevas.