Autoregulation of Free Radicals via Uncoupling Protein Control in Pancreatic β-Cell Mitochondria

Abstract

Pancreatic β-cells sense the ambient blood-glucose concentration and secrete insulin to signal other tissues to take up glucose. Mitochondria play a key role in this response as they metabolize nutrients to produce ATP and reactive oxygen species (ROS), both of which are involved in insulin secretion signaling. Based on data available in the literature and previously developed mathematical models, we present a model of glucose-stimulated mitochondrial respiration, ATP synthesis, and ROS production and control in β-cells. The model is consistent with a number of experimental observations reported in the literature. Most notably, it captures the nonlinear rise in the proton leak rate at high membrane potential and the increase in this leak due to uncoupling protein (UCP) activation by ROS. The functional forms used to model ROS production and UCP regulation yield insight into these mechanisms, as many details have not yet been unraveled in the experimental literature. We examine short- and long-term effects of UCP activation inhibition and changes in the mitochondrial density on mitochondrial responses to glucose. Results suggest increasing mitochondrial density while decreasing UCP activity may be an effective way to increase glucose-stimulated insulin secretion while decreasing oxidative stress.

Introduction

Mitochondria are the main source of free radicals known as reactive oxygen species (ROS), such as superoxide, hydrogen peroxide, and hydroxyl radical, within most cells (1). ROS production in mitochondria is sensitive to the proton motive force and ROS concentration is regulated by scavenging enzymes (SE) and the activation of uncoupling proteins (UCP), which decrease the mitochondrial inner membrane potential (ΔΨ). The tissue-damaging effects of ROS have been hypothesized to underlie many well-defined diseases and clinically relevant complications, including those associated with diabetes, Parkinson's disease, Alzheimer's disease, myopathy, and atherosclerosis (2,3). ROS have also been shown to play important signaling roles, such as in mitochondrial biogenesis (4), longevity (5,6), mitochondrial evolution and adaptation (3,7), and insulin secretion (8,9). Therefore, tight regulation of ROS is important to minimize damage without impacting signaling (8).

There is evidence to suggest that ROS and UCP play a key role in pancreatic β-cell dysfunction under various environmental conditions (8–13). Beta cells are glucose-responsive cells that sense the ambient plasma-glucose concentration and secrete insulin to signal other tissues to take up glucose (10,12). An increase in plasma-glucose levels leads to an increase in the fluxes through the glycolytic and mitochondrial metabolism pathways and an increase in the cellular ATP/ADP ratio. This causes a series of events to occur in which ATP-sensitive potassium channels close, voltage-gated calcium channels open, and insulin secretion is triggered (10,12). Environmental factors, such as low physical activity and hypercaloric lipid-rich diets, are associated with insulin resistance and decreased glucose-stimulated insulin secretion in the long term (11,13,14). Therefore, knowing how ROS and UCP contribute to β-cell function and insulin secretion, subject to the environment, is important (8–13).

Fig. 1 illustrates the mitochondrial pathways involved in the glucose-sensing process that are relevant to the model presented here. Beta cells take up glucose (Glu) molecules from the bloodstream and convert them to pyruvate, via glycolysis, readying them for the mitochondria. Once these glycolytic end-products are in the mitochondria, the hydrogen atoms are removed from the hydrocarbons in the tricarboxylic acid (TCA) cycle to produce NADH and FADH₂. Calcium, which is injected into mitochondria by the Ca²⁺ uniporter and ejected by the Na⁺/Ca²⁺ exchanger (NaCa), has both depolarizing (electrical) and hyperpolarizing (increasing activity of pyruvate dehydrogenase and key TCA enzymes (15)) effects on mitochondria (16).

Figure 1.

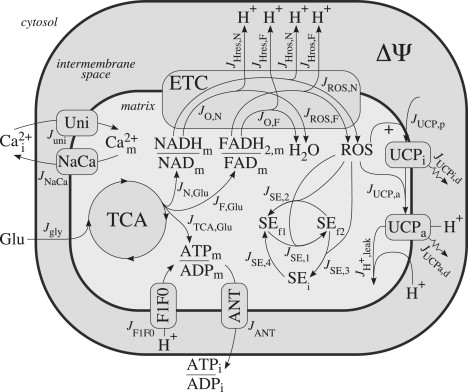
Illustration of mitochondrial processes involved in glucose sensing and relevant to the model presented here. Glu, plasma glucose; TCA, tricarboxylic acid cycle; Ca_i, intracellular calcium; Ca_m, mitochondrial calcium; Uni, Ca²⁺ uniporter; NaCa, Na⁺/Ca²⁺ exchanger; ETC, electron transport chain; H⁺, protons; ROS, reactive oxygen species, ΔΨ, mitochondrial inner membrane potential; UCP_i, inactive uncoupling protein; UCP_a, active uncoupling protein; SE_f1, oxidized scavenging enzyme; SE_f2, reduced scavenging enzyme; SE_i, inhibited scavenging enzyme; ANT, adenine nucleotide translocator; and F1F0, F₁F₀-ATP synthase.

The electron donors, NADH and FADH₂, contribute their electrons to the electron transport chain (ETC). As the electrons flow through the ETC, protons (H⁺) are pumped from the mitochondrial matrix to the intermembrane space, increasing ΔΨ. Once protons are in the intermembrane space, they can flow down the energy gradient, back into the matrix, through the F₁F₀-ATP synthase (F1F0). In this process, the energy stored in the proton gradient is used to do work by driving the phosphorylation of ADP to ATP. ATP produced in the mitochondria is transported out of the matrix by the adenine nucleotide translocator (ANT).

Normally, the electrons flowing through the ETC are passed on to complex IV and used to reduce a single oxygen atom to make H₂O, but occasionally (and particularly at high ΔΨ) before reaching that point they can react directly with molecular oxygen to produce superoxide: the primary form of ROS produced in mitochondria (1,17). ROS can be removed by antioxidants, i.e., SE, or they can activate UCP and cause protons to leak back into the matrix, thus diverting them from the ATP production process. This leak is in addition to the basal leak that occurs at all times, as we further describe below.

A much larger proportion of the overall respiratory activity is wasted as proton leak in β-cells than in other cell types, including hepatocytes, thymocytes, neurons, and muscle (18,19). It has been shown that this proton leak more strongly controls the ATP/ADP ratio in β-cells than in muscle (19), and UCP (primarily UCP2 in the β-cell) contributes substantially to the proton leak in β-cells (18). UCP can be activated by ROS and fatty acids (20), although the details of the activation and proton transport mechanism are not yet clear (21). Purine nucleotides (such as GDP) have classically been considered specific inhibitors of UCP, but recent experimental results have shown that this is not the case (22). Results from whole-body UCP2-knockout mice have provided evidence for the role that UCP2 plays in glucose-stimulated insulin secretion (8,10), but β-cell specific knockouts have not yet been developed.

To investigate the roles of ROS and UCP regulation in response to nutrient inputs in β-cells, we developed a mathematical model based on previously derived models (16,23–25) and the current published data (18–20,26). The model captures the behavior of mitochondrial respiration and ATP synthesis, and goes beyond the previously developed models to include dynamics related to ROS production and the SE and UCP defense mechanisms (Fig. 1 and Modeling Methods). We parameterize the model using experimental results of UCP content and the proton leak rate from the literature (Modeling Methods). To our knowledge, mechanistic details of the processes of ROS production and UCP regulation have not yet been fully experimentally elucidated in the literature. The fact that the mathematical model can match existing experimental observations implies that the functional forms of the fluxes used in the model are sufficient to capture the behaviors observed in experiments without requiring more complicated or detailed mechanistic relationships. Finally, we use the model to investigate the effects of UCP and mitochondrial density on ROS and ATP production in response to glucose (Results).

Modeling Methods

The model presented here builds upon previously developed mathematical models (16,23–25). Assuming a constant mitochondrial volume, the governing dynamic equations for the concentrations of the mitochondrial variables and the inner membrane potential are as follows. The mitochondrial NADH and FADH₂ concentrations, NADH_m and FADH_2,m (mM), respectively, change according to

$$\frac{\text{d}NAD{H}_{\text{m}}}{\text{d}t}=\gamma \left(J_{\text{N},\text{Glu}}-J_{\text{O},\text{N}}-J_{\text{ROS},\text{N}}\right),$$ (1)

$$\frac{\text{d}FAD{H}_{2,\text{m}}}{\text{d}t}=\gamma \left(J_{\text{F},\text{Glu}}-J_{\text{O},\text{F}}-J_{\text{ROS},\text{F}}\right),$$ (2)

where J_N,Glu is the glucose-dependent NADH production rate, J_O,N is the rate of oxidation of NADH that results in the consumption of a single oxygen atom to produce H₂O, J_ROS,N is the NADH-dependent rate of ROS production, and J_F,Glu, J_O,F, and J_ROS,F are the corresponding FADH₂-related rates. Each of the fluxes noted here and below are in units of μM/ms. The value γ = 0.001 mM/μM is used to convert μM to mM units.

The mitochondrial Ca²⁺ concentration, Ca_m (μM), changes according to

$$\frac{\text{d}C{a}_{\text{m}}}{\text{d}t}=f_{\text{m}}\left(J_{\text{uni}}-J_{\text{NaCa}}\right),$$ (3)

where J_uni and J_NaCa correspond to the uniporter and Na⁺/Ca²⁺ exchanger rates, respectively. The value f_m = 0.0003 is the fraction of free mitochondrial Ca²⁺ (23).

The mitochondrial ATP concentration, ATP_m (mM), changes according to

$$\frac{\text{d}AT{P}_{\text{m}}}{\text{d}t}=\gamma \left(J_{\text{TCA},\text{Glu}}+J_{\text{F1F0}}-J_{\text{ANT}}\right),$$ (4)

where ATP is produced from the TCA cycle (assuming immediate conversion from GTP) and the F₁F₀-ATP synthase at the rates J_TCA,Glu and J_F1F0, respectively, and taken out of the matrix by the ANT at the rate J_ANT.

Superoxide, being the primary form of reactive oxygen species produced in mitochondria (1), is the form we are most interested in modeling, and the one that we generally refer to as “ROS” hereafter. ROS levels increase with the fluxes J_ROS,N and J_ROS,F, and decrease through scavenging removal at the rate J_SE,1 + J_SE,2 + J_SE,3 and UCP activation at the rate J_UCP,a, giving

$$\frac{\text{d}ROS}{\text{d}t}=2\left(J_{\text{ROS},\text{N}}+J_{\text{ROS},\text{F}}\right)-J_{\text{SE},1}-J_{\text{SE},2}-J_{\text{SE},3}-J_{\text{UCP},\text{a}}\text{.}$$ (5)

The stoichiometric factor of two corresponds to two ROS produced per two NADH or FADH₂ electrons, as described below. ROS represents the ROS concentration (μM).

Manganese superoxide dismutase is the scavenging enzyme that catalyzes the removal of superoxide, and we generally refer to it as “SE” hereafter. The oxidized and reduced SE concentrations, SE_f1 and SE_f2 (μM), respectively, change according to the scavenging reaction rates, J_SE,1, J_SE,2, J_SE,3, and J_SE,4, such that

$$\frac{\text{d}S{E}_{\text{f}1}}{\text{d}t}=J_{\text{SE},2}+J_{\text{SE},4}-J_{\text{SE},1},$$ (6)

$$\frac{\text{d}S{E}_{\text{f}2}}{\text{d}t}=J_{\text{SE},1}-J_{\text{SE},2}-J_{\text{SE},3}\text{.}$$ (7)

Beta cells primarily express UCP2, and it is this form of uncoupling protein that we generally refer to as “UCP” hereafter. Inactive and active UCP concentrations, UCP_i and UCP_a (μM), respectively, change according to

$$\frac{\text{d}UC{P}_{\text{i}}}{\text{d}t}=J_{\text{UCP},\text{p}}-J_{\text{UCP},\text{a}}-J_{\text{UCPi},\text{d}},$$ (8)

$$\frac{\text{d}UC{P}_{\text{a}}}{\text{d}t}=J_{\text{UCP},\text{a}}-J_{\text{UCPa},\text{d}},$$ (9)

where inactive UCP are produced at the rate J_UCP,p, UCP are activated at the rate J_UCP,a, and both forms decay at their respective rates J_UCPi,d and J_UCPa,d.

The energy stored across the inner membrane, i.e., the proton motive force, has voltage (ΔΨ) and pH (ΔpH) components. Past models have taken ΔpH to be constant (23,25), and experimental results used here to parameterize our model were typically obtained after the addition of a chemical (nigericin) to collapse ΔpH (18–20). We, therefore, only consider changes in ΔΨ, but dependencies on ΔΨ can be replaced to include a variable ΔpH (as was the case in Cortassa et al. (24)) for more general applications. The mitochondrial membrane potential changes according to

$$\frac{\text{d}\Delta \Psi }{\text{d}t}=(J_{\text{Hres},\text{N}}+J_{\text{Hres},\text{F}}+J_{\text{Hros},\text{N}}+J_{\text{Hros},\text{F}}-J_{\text{H},\text{ATP}}-J_{{\text{H}}^{+},\text{leak}}-J_{\text{ANT}}-J_{\text{NaCa}}-2J_{\text{uni}})/C_{\text{m}},$$ (10)

where J_Hres,N, J_Hres,F, J_Hros,N, J_Hros,F, and J_H,ATP are the proton effluxes from the matrix to the intermembrane space associated with J_O,N, J_O,F, J_ROS,N, J_ROS,F, and J_F1F0, respectively, and J_H⁺,_leak is the proton leak rate. C_m = 1.8 μM/mV is the mitochondrial capacitance (23).

We assume conservation of the mitochondrial concentrations (23,24,27,28)

$$NA{D}_{\text{tot}}=NA{D}_{\text{m}}+NAD{H}_{\text{m}}=10\text{mM},$$ (11)

$$FA{D}_{\text{tot}}=FA{D}_{\text{m}}+FAD{H}_{2,\text{m}}=2.75\text{mM},$$ (12)

$$A_{\text{tot}}=AD{P}_{\text{m}}+AT{P}_{\text{m}}=15\text{mM},$$ (13)

$$S{E}_{\text{tot}}=S{E}_{\text{f1}}+S{E}_{\text{f2}}+S{E}_{\text{i}}=0.7\mu \text{M,}$$ (14)

where NAD_m, FAD_m, and ADP_m are the mitochondrial NAD⁺, FAD, and ADP concentrations (mM), respectively, and SE_i is the concentration of inhibited SE (μM).

Those fluxes in Eqs. 1–10 that were simplified from previously developed models are described in detail in the Appendix. In the following subsections, we describe the fluxes related to ROS, SE, and UCP, which have not been previously modeled. Each parameter value used in the model is given in Table 1.

Table 1.

Model parameters

Parameter	Value	Units	Ref.
γ	0.001	mM/μM	—
fm	0.0003	Unitless	(23)
Cm	1.8	μM/mV	(23)
NADtot	10	mM	(23)
FADtot	2.75	mM	(24,27)
Atot	15	mM	(23)
SEtot	0.7	μM	(28)
τ	10	min	(27)
p1	6	μM/ms	(23)
p2	141	mV	(16,19,23)
p3	5	mV	(16,19,23)
p4	0.37	μM/ms	(23,24)
p5	0.5	Unitless	—
p6	1.5	/μM/ms	(26)
p7	0.55	/μM/ms	(26)
p8	0.117	/ms	(26)
p9	5.5 × 10−8	/ms	(29)
p10	5.3 × 10−8	μM/ms	(29)
p11	2.5 × 10−6	/μM/ms	(18,29)
p12	1.93 × 10−7	/ms	(29)
p13	0.0214	/mV	(18–20)
p14	8.4 × 10−4	μM/ms/mV	(18–20)
p15	0.0014	/ms/mV	(18–20,29)
p16	0.03	/μM/ms	(23,25)
p17	0.023	/mV	(23,25)
p18	0.03	μM/ms	(23,25)
p19	3.752	μM	(23,25)
p20	0.0185	/mV	(23,25)
p21	0.035	μM/ms	(25)
p22	0.531	Unitless	(25)
p23	0.1	μM	(25)
p24	12.171	μM/ms	(16,18,23)
p25	0.0114	Unitless	(16,18,23)
p26	154	mV	(16,18,23)
p27	8.5	mV	(16,18,23)
p28	2.554	μM/ms	(23)
p29	0.151	Unitless	(23)
p30	9.25 × 10−4	/mV	(23)

ROS production

As ΔΨ increases, it becomes more difficult for the ETC complexes to pump protons against that potential. Instead of completing their trip through the ETC, electrons in the ETC begin reacting directly with molecular oxygen, reducing it to form superoxide. Although several details of mitochondrial ROS production have been revealed, exact mechanisms remain obscure (1,17). We, therefore, model the ROS production rate phenomenologically, based on the form of the NADH_m and FADH_{2, m} oxidation rates in Eqs. 32 and 34, as

$$J_{\text{ROS},\text{N}}=p_1{\left(\frac{NAD{H}_{\text{m}}}{NA{D}_{\text{m}}}\right)}^{1/2}\left(1-\frac{1}{1+e^{\left(\Delta \Psi -p_2\right)/p_3}}\right),$$ (15)

$$J_{\text{ROS},\text{F}}=p_4{\left(\frac{FAD{H}_{2,\text{m}}}{FA{D}_{\text{m}}}\right)}^{1/2}\left(1-\frac{1}{1+e^{\left(\Delta \Psi -p_2\right)/p_3}}\right),$$ (16)

respectively, where p₁ = 6 μM/ms, p₂ = 141 mV, p₃ = 5 mV, and p₄ = 0.37 μM/ms. The parameters were estimated from the NADH_m and FADH_2,m oxidation rates of previously developed models and (in the case of p₂) by fitting data from the literature, as described in the Appendix. Because each of the electrons donated by NADH_m and FADH_2,m react with molecular oxygen to yield a superoxide, a factor of two is reflected with each of these rates in Eq. 5. Fig. 2 illustrates the ROS production rate that results from NADH_m oxidation. That from FADH_2,m oxidation has the same qualitative behavior.

Figure 2.

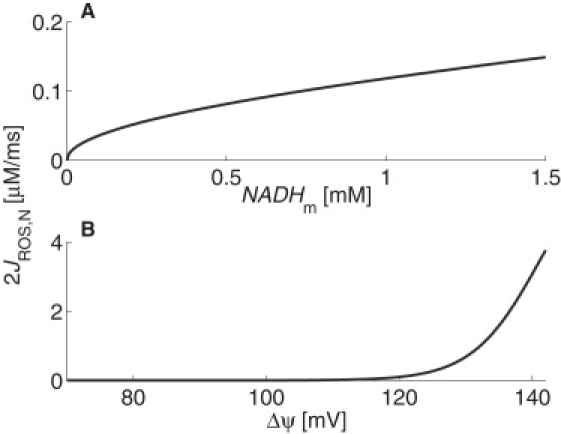
ROS production rate from NADH_m oxidation for physiological (A) concentrations of NADH_m (ΔΨ = 120 mV) and (B) ΔΨ (NADH_m = 0.75 mM).

The electrons do not complete the ETC circuit when ROS are produced. Instead, they can be diverted from their course at various points, such as, for example, the electron transfer points of complex III (1,17). This means that fewer protons may be pumped out of the mitochondrial matrix when ROS are produced, depending on when the electrons exit the ETC, than when NADH_m and FADH_2,m oxidation produces H₂O. Because, to our knowledge, no experimental evidence exists to quantify the number of protons pumped out of the matrix when ROS are produced, we estimate that, on average, it results in only half of the protons being pumped out than would be when the case H₂O is produced. Therefore, we model the rate of proton efflux resulting from the oxidation of NADH_m and FADH_2,m to produce ROS as

$$J_{\text{Hros},\text{N}}=12p_5{J}_{\text{ROS},\text{N}},$$ (17)

$$J_{\text{Hros},\text{F}}=8p_5{J}_{\text{ROS},\text{F}},$$ (18)

respectively, based on the form of Eqs. 33 and 35, where p₅ = 0.5. These rates have the same qualitative behavior as J_ROS,N and J_ROS,F (Fig. 2). Deviations in the value of p₅ do not significantly impact the overall qualitative behavior of the model, as the contribution from the ROS production process to the total number of protons being pumped out of the matrix during NADH_m and FADH_2,m oxidation is relatively small under normal conditions. Simulations of the complete model with p₅ taken to the extreme values of 0 or 1 resulted in miniscule changes (<0.5%) in ΔΨ at the highest glucose concentrations (20 mM) examined below.

Scavenging enzymes

Once ROS are produced, they can be removed from the system by SE. Manganese superoxide dismutase catalyzes the dismutation of two superoxides into oxygen and hydrogen peroxide as it cycles (reactions J_SE,1 and J_SE,2 in Fig. 1) between oxidized and reduced forms, which we call SE_f1 and SE_f2, respectively. SE_f2 can become inhibited to form SE_i when it reacts with ROS (reaction J_SE,3 in Fig. 1), but the inhibited form can become active one again (J_SE,4 in Fig. 1). We use the scheme shown in the central part of Fig. 1, with mass action relationships and rate parameters measured by Hearn et al. (26), to model the rates associated with the process of ROS removal by SE as

$$J_{\text{SE},\text{1}}=p_{6}S{E}_{\text{f}1}ROS,$$ (19)

$$J_{\text{SE},\text{2}}=J_{\text{SE},3}=p_{7}S{E}_{\text{f}2}ROS,$$ (20)

$$J_{\text{SE},\text{4}}=p_{8}S{E}_{\text{i}},$$ (21)

where p₆ = 1.5/μM/ms, p₇ = 0.55/μM/ms, and p₈ = 0.117/ms.

UCP regulation and proton leak

UCP are dynamically regulated in β-cells, with concentrations increasing with sustained increases in nutrient level exposure (11,13,29). They remain in an inactive state unless acted upon by endogenous activators, such as ROS and fatty acids (20). UCP have a short half-life of ∼60 min, and this is thought to be the mechanism through which the activated UCP proton leak ceases (29). Here, we assume ROS serves as a signal for UCP production and it is responsible for UCP activation. We model the UCP regulation processes according to the scheme shown on the right of Fig. 1, with the rates of UCP production (J_UCP,p), activation (J_UCP,a), and decay (J_UCPi,d and J_UCPa,d) given by

$$J_{\text{UCP},\text{p}}=p_{9}RO{S}_{\text{delay}}+p_{10},$$ (22)

$$J_{\text{UCP},\text{a}}=p_{11}UC{P}_{\text{i}}ROS,$$ (23)

$$J_{\text{UCP},\text{d}}=p_{12}UC{P}_{\text{i}},$$ (24)

$$J_{\text{UCPa},\text{d}}=p_{12}UC{P}_{\text{a}},$$ (25)

respectively. The parameter values, p₉ = 5.5 × 10⁻⁸/ms, p₁₀ = 5.3 × 10⁻⁸ μM/ms, and p₁₁ = 2.5 × 10⁻⁶/μM/ms, were determined by running simulations of the complete model and performing a least-squares fit of the steady-state UCP_tot = UCP_i + UCP_a to data from the literature (29), as shown in Fig. 3. The parameter p₁₂ = 1.93 × 10⁻⁷/ms was measured experimentally by Azzu et al. (29). ROS_delay(t) = ROS(t – τ) is a delay variable that follows ROS levels, where τ > 0 accounts for the time it would take for the signal to propagate and for UCP to be translated and inserted into the membrane. In the results shown below, we estimate τ = 10 min (27).

Figure 3.

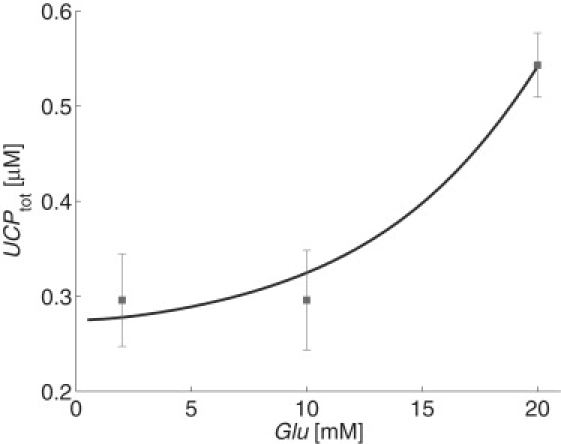
Steady-state simulations were run for fixed glucose concentrations and total UCP content was calculated. Intracellular calcium was held constant at 0.2 μM. Data from Azzu et al. (29) are shown for comparison.

Activated UCP contributes to the leak of protons from the intermembrane space to the matrix, effectively decreasing ΔΨ and diverting protons from the ATP production process while reducing the rate of ROS production (13,20). This is a defense mechanism implemented through ROS self-regulation by negative feedback. The proton leak rate is a nonlinear, ΔΨ-dependent rate. It has an active UCP component and a basal component, which we assume includes the leak through ANT and other pathways. Although the basal leak rate is energization-dependent (22), this dependence is not yet well understood. Because we are primarily interested in the effects of UCP-mediated leak beyond the basal leak, we consider the basal leak component to be dependent only on ΔΨ in our model. We model the proton leak rate as

$$J_{{\text{H}}^{+},\text{leak}}=\Delta \Psi e^{p_{13}\Delta \Psi }\left(p_{14}+p_{15}UC{P}_{\text{a}}\right)\text{.}$$ (26)

Fig. 4 illustrates the steady-state ΔΨ dependence of J_H⁺,_leak for Glu = 11 mM and Ca_m = 0.3 μM. The solid curve in Fig. 4, $J_{{\text{H}}^{+},\text{leak}}=0.0012\Delta \Psi \text{exp}\left(0.0214\Delta \Psi \right)$, was fit by least-squares to β-cell proton leak rate measurements from Echtay et al. (20) and Affourtit and Brand (18,19) (shown in Fig. 4 as squares, circles, and triangles, respectively). An estimate that UCP accounts for 30% of the proton leak rate in β-cells grown in 11 mM glucose (18) was then used to determine p₁₃ = 0.0214/mV and p₁₄ = 8.4 × 10⁻⁴ μM/ms/mV. The dashed curve in Fig. 4 shows the proton leak rate in the absence of UCP. The parameter p₁₅ = 0.0014/ms/mV was determined in combination with p₉, p₁₀, and p₁₁, by fitting data related to UCP_tot, as described above, with the constraint that p₁₅UCP_a = 3.6 × 10⁻⁴ μM/ms/mV at Glu = 11 mM and Ca_m = 0.3 μM.

Figure 4.

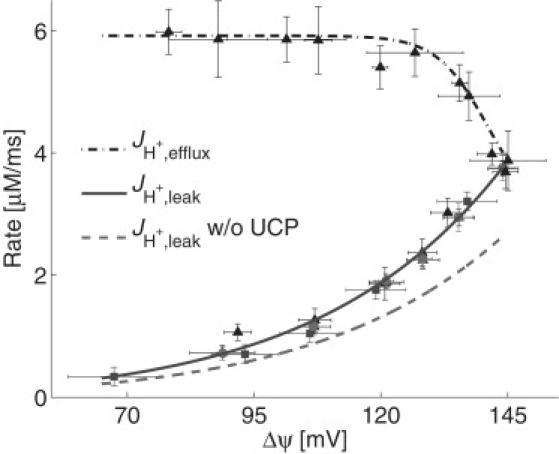
The nonlinear proton-leak rate in the absence (dashed curve) and presence (solid curve) of UCP and the proton efflux rate, J_H⁺, _efflux = J_Hres,N + J_Hres,F + J_Hros,N + J_Hros,F (dash-dotted curve), are shown for steady-state model simulations as a function of ΔΨ with Glu = 11 mM and Ca_m = 0.3 μM. Data from Echtay et al. (20) (squares), Affourtit and Brand (18) (circles), and Affourtit and Brand (19) (triangles) are shown for comparison.

Model implementation

The model is implemented in MATLAB (The MathWorks, Natick, MA) and available at http://lbm.niddk.nih.gov/heuettw/wjh/Publications.html. Least-squares calculations used to determine p₂, p₉, p₁₀, p₁₁, p₁₃, p₁₄, and p₁₅ were performed using the MATLAB optimization toolkit.

Results

Inhibiting UCP activation

Pancreatic β-cells secrete insulin when stimulated by increasing plasma-glucose levels: a response mediated by an increase in the intracellular ATP/ADP ratio. Given that UCP divert protons from ATP production, and thus from the insulin secretion signal, it may be thought that inhibiting UCP expression or activity is a possible therapeutic approach to improve glucose-stimulated insulin secretion (10). We examined the long-term effect of inhibiting UCP activation by perturbing the parameter p₁₁ in our model from its original value of 2.5 × 10⁻⁶/μM/ms, and comparing the mitochondrial variables' steady-state responses to glucose levels under normal and inhibited UCP activation scenarios. Fig. 5 shows the results for the normal UCP activation case (solid curves) and the cases in which UCP activation was inhibited by 90% (dashed curves) and 100% (dash-dotted curves).

Figure 5.

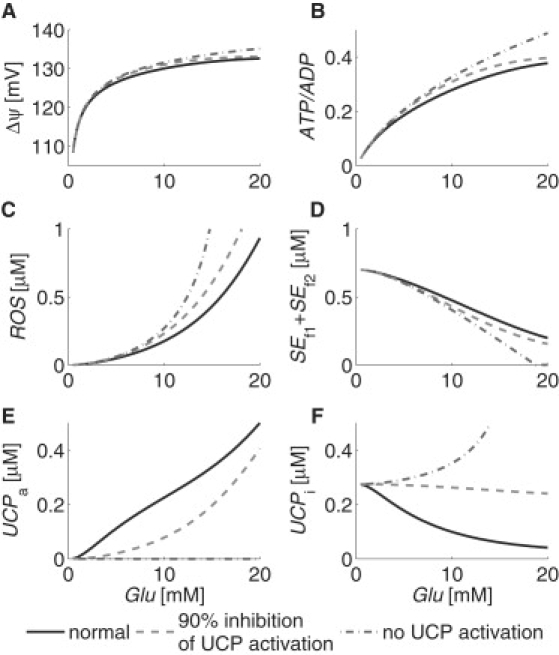
Simulations of mitochondrial (A) ΔΨ, (B) ATP/ADP, (C) ROS, (D) SE_f1 + SE_f2, (E) UCP_a, and (F) UCP_i steady-state responses to plasma glucose with normal (solid curves) and inhibited (dashed and dash-dotted curves) UCP activation. Intracellular calcium was held constant at 0.2 μM.

Model simulations show that as the plasma-glucose level increases, so does the mitochondrial membrane potential (Fig. 5 A) and the ATP/ADP ratio (Fig. 5 B). Increasing ΔΨ increases mitochondrial ROS production (Fig. 5 C), which challenges the SE and UCP defense mechanisms (Fig. 5, D–F). Inhibiting UCP shifts the ATP/ADP ratio curve up, and increases the rate at which it increases with respect to glucose. Between Glu = 5 mM and 10 mM, the ATP/ADP ratio increases by 50% under normal conditions, by 52% when UCP activation is inhibited by 90%, and by 58% when UCP activation is completely inhibited. This shows that blocking UCP activation increases the ATP/ADP ratio, and might be expected to increase the glucose-stimulated insulin secretion response. The negative side effect of blocking UCP activation is that ROS levels are also increased to the point that there is 25% more ROS at Glu = 5 mM when there is no UCP activation than when UCP is activated normally. Long-term exposure to these increased ROS levels would be expected to cause additional oxidative damage. This is in fact the case according to experiments, which have shown that the chronic absence of UCP causes persistent oxidative stress and impairment of β-cell function (8).

Increasing mitochondrial density

Experimental observations have attributed an increase in mitochondrial function to an increase in mitochondrial density, i.e., the mitochondrial content of a cell (30). We investigated the long-term effects of changes in the mitochondrial content of a cell by dividing our model parameters p₁₆, p₁₈, p₂₁, and p₂₈ by a mitochondrial density parameter, which we call p₀, where p₀ = 1 represents the typical mitochondrial content, and p₀ > 1 represents a proportional increase in mitochondrial content. We then compared the mitochondrial variables' steady-state responses to glucose levels under normal and increased mitochondrial density scenarios. Fig. 6 shows the results for the normal mitochondrial content case (solid curves), the effects of increasing the mitochondrial density by one-third (dashed curves), and the combined effects of such an increase with complete inhibition of UCP activation (dash-dotted curves).

Figure 6.

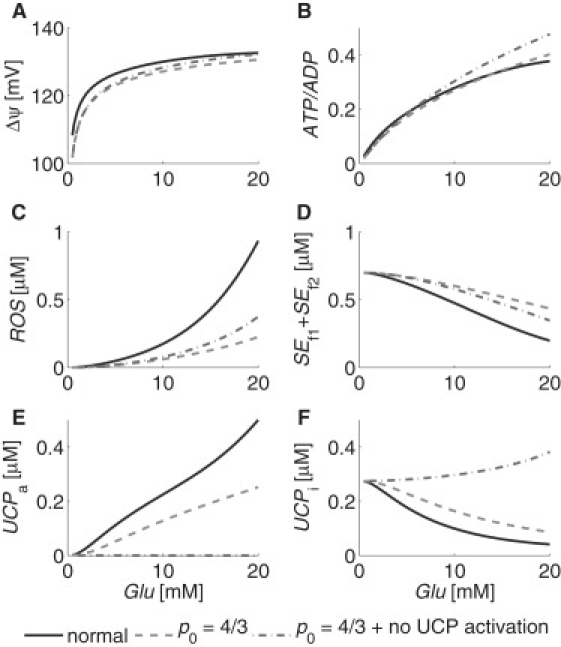
Simulations of mitochondrial (A) ΔΨ, (B) ATP/ADP, (C) ROS, (D) SE_f1 + SE_f2, (E) UCP_a, and (F) UCP_i steady-state responses to plasma glucose with normal (solid curves) and increased (dashed and dash-dotted curves) mitochondrial density, p₀. The value p₀ = 1 represents normal mitochondrial density. Dash-dotted curves show the combined effects of complete UCP activation inhibition with an increase in p₀. Intracellular calcium was held constant at 0.2 μM.

Increasing the mitochondrial density by one-third, i.e., setting p₀ = 4/3, increases the rate at which the ATP/ADP ratio increases with respect to glucose, such that the ratio increases by 58% between Glu = 5 mM and 10 mM, as compared to the 50% increase under normal conditions discussed above. At the same time, ROS levels are decreased to the point that there is 64% less ROS at Glu = 5 mM when p₀ = 4/3 than to when p₀ = 1. The rate at which the ATP/ADP ratio increases with respect to glucose increases even further when both the mitochondrial density is increased by one-third and UCP activation is completely blocked (i.e., p₀ = 4/3 and p₁₁ = 0), such that the ratio increases by 67% between Glu = 5 mM and 10 mM. ROS levels in this case remain low, at 59% less than that of normal conditions. These results suggest that an increase in mitochondrial density can increase mitochondrial function, primarily by distributing the metabolic load among more mitochondria, and may increase glucose-stimulated insulin secretion while decreasing oxidative stress.

Short-term responses to a glucose profile

Generally, experiments examining mitochondrial ROS and UCP regulation deal with long-term exposure to nutrient levels (10–13), but ROS have been shown to have important temporal roles as signals in response to glucose in β-cells (8,9). To examine the effects of blocking UCP activation and increasing the mitochondrial density in the short term, we simulated the mitochondrial variables' responses to a glucose profile measured by Breda et al. (31). The glucose profile was measured for a total of 300 min, starting from an initial value of Glu = 5.4 mM, and reaching a maximum of Glu = 9.5 mM at 60 min. We assumed that the initial conditions for the simulations were resting, steady-state conditions determined by the initial glucose concentration. Fig. 7 shows the glucose profile and the results of the simulations for normal UCP activation and mitochondrial density (solid curves), complete inhibition of UCP activation (dashed curves), and complete inhibition of UCP activation in combination with an increase of one-third in the mitochondrial density (dash-dotted curves). In the cases involving inhibition of UCP activation, the inhibition was assumed to occur instantaneously and completely, i.e., p₁₁ → 0, at time 0 min, and to persist throughout the 300-min simulation.

Figure 7.

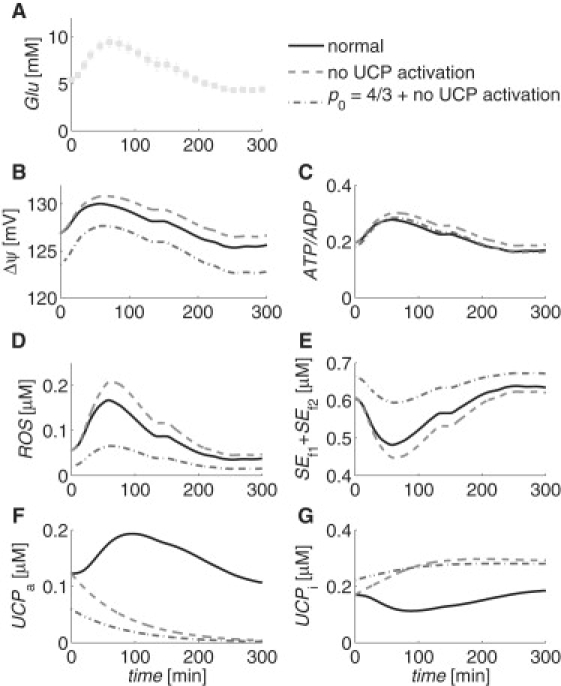
Simulations of mitochondrial (B) ΔΨ, (C) ATP/ADP, (D) ROS, (E) SE_f1 + SE_f2, (F) UCP_a, and (G) UCP_i time-dependent responses to (A) a plasma glucose profile from Breda et al. (31), under normal (solid curves) and inhibited (dashed and dash-dotted curves) UCP activation conditions. Dash-dotted curves show the combined effects of complete UCP activation inhibition with an increase of one-third in the mitochondrial density, p₀. Intracellular calcium was held constant at 0.2 μM.

Model simulations show that ROS increases in the short term to a maximum of three times its initial value under normal UCP activation and mitochondrial density conditions. Starting from the same initial condition, the sudden blocking of UCP activation causes a larger increase in ROS to 3.7 times the initial value. This supports the suggestion put forward by Pi et al. (8), that although long-term absence of UCP can cause persistent oxidative stress and impair β-cell function, the acute inhibition of UCP activation may allow for a greater ROS signal, and perhaps an improved glucose-stimulated insulin secretion response. The combination of the sudden blocking of UCP activation with a persistent one-third increase in the mitochondrial density, i.e., p₀ = 4/3, causes an increase in ROS to 3.2-times its initial value, but the initial value for this case has a lower initial, steady-state ROS value that is 64% less than the other two cases because of the increased mitochondrial density.

For each of the short-term simulations discussed above, we estimated the parameter τ was 10 min. Additional simulations (not shown) were performed for other values of τ between 0 and 150 min, assuming normal UCP activation and mitochondrial density. Such variations resulted in no qualitative differences and only miniscule changes (<0.5%) in all the mitochondrial variables at their peak values, with the exception of the UCP variables, which were shifted in time according to τ. In all cases, there was sufficient UCP_i available to meet demand in response to ROS levels, and UCP_tot = UCP_i + UCP_a increased to a maximum of only 5% more than its initial value at time 0 min, regardless of τ.

Discussion

Mitochondria play a key role in whole-body metabolism: a complex process involving many different tissues, such as muscle, fat, liver, and pancreas, in an intimate relationship between signaling pathways and metabolic networks (14). Mitochondrial dysfunction can result from several factors, including oxidative stress, which inhibits the ability of mitochondria to maintain ΔΨ (3). Emerging evidence supports the hypothesis that mitochondrial dysfunction causes insulin resistance and hyperglycemia: prominent features of type 2 diabetes (14). Such analyses have emphasized the critical roles of ROS, UCP, and mitochondrial density in disease progression.

Although many of the details of mitochondrial ROS production and UCP regulation are still being unraveled experimentally, we developed a state-of-the-data model, based on the data and information available, to integrate the current understanding and make predictions about the system. The model goes beyond previously developed models by incorporating ROS production and the activity of SE and UCP. Importantly, it captures the nonlinear behavior of the proton-leak rate as a function of membrane potential and UCP activity. The model's simplicity is an advantage in that it allows easy manipulation and transference (i.e., through parameter adjustments), making it useful for research on the integrative physiology of mitochondria. Having been developed for β-cell mitochondria, the model allows us to make inferences and propose hypotheses related to the roles ROS, UCP, and mitochondrial density play in β-cell function and insulin secretion under various environmental conditions.

The functional forms used to model ROS production, UCP regulation, and proton leak rates are important. Many details related to these mechanisms are still unknown in the experimental literature. We based the form of the ROS production fluxes on those of the NADH and FADH₂ oxidation rates, and used simple mass action relationships, without saturation, cooperativity, or other more complicated relationships, to model UCP production, activation, and decay. The fact that the model can match reasonably complex experimental data implies that the functional forms used contain enough detail, without requiring the burden of more complicated relationships, to capture the existing experimental observations within physiological ranges. In turn, these functional forms may provide useful insight to enhance experimental deductions.

Model simulations can be used to examine the short- and long-term effects that perturbations in UCP activity and mitochondrial density have on β-cell function. They predict that short-term inhibition of UCP will prevent the diversion of protons from ATP production and enhance ROS signaling. Such a response may improve glucose-stimulated insulin secretion (8). However, long-term inhibition of UCP is predicted to cause a sustained increase in ROS levels, and would therefore be expected to cause persistent oxidative stress. By increasing the mitochondrial density within the cell, the metabolic load can be shared among more mitochondria, and it is predicted that this serves to increase the ATP/ADP ratio response to glucose while decreasing oxidative stress. Experimentally, the perturbations in UCP activity and mitochondrial density could potentially be accomplished using pharmacological UCP inhibitors, such as genipin (32), and activators of the sirtuin, SIRT1, and the peroxisome proliferator-activated receptor-γ coactivator, PGC1α, which regulate mitochondrial biogenesis (4,6).

There are multiple limitations to the current model, such as it does not include adaptive responses, such as increases in antioxidant levels in response to elevated ROS levels (8), which might occur in living cells. We only considered superoxide as the endogenous UCP activator here, but other potential activators, e.g., other forms of ROS, such as hydroxynonenal, and fatty acids, have been identified experimentally (20,22). Although the intracellular calcium level was held constant for the simulations presented, it would actually be expected to vary and experience bursts and oscillations in response to glucose (25), potentially exaggerating the results shown here, given the polarizing effects calcium has on mitochondria (15,16). We also neglected the ΔpH component of the proton motive force (18–20,23,24) and the energization-dependent properties of ANT and other pathways in the proton leak rate (18,22), for reasons discussed in Modeling Methods. These and more are acknowledged limitations, but each limitation can and will be addressed in future generations of the model.

The fact that common human diseases and changes in metabolic states are often associated with relatively small changes in many enzymes, rather than twofold or greater changes in only a few enzymes, illustrates the crucial importance of quantitative modeling in their investigation. The model presented here provides a way to test the current understanding of a complex system, and examine how perturbations may affect the system over time.

Appendix

Much of the basis of our model comes from a model originally derived by Magnus and Keizer (23,25). We have simplified their model by making several approximations, similar to those made by Bertram et al. (16), as described below. Because β-cells operate at lower membrane potentials than skeletal muscle and cardiac cells, and because the earlier models were developed using data from the latter, the inflection points of the ΔΨ-dependent curves from the earlier models were adjusted. We used the factors g₁ and g₂ as described below, to better agree with the experimental observations of the ΔΨ-dependence of the proton efflux rate, J_H⁺,_efflux, in β-cells, as measured by Affourtit and Brand (19) and shown in Fig. 4. Magnus and Keizer (23) noted that these factors may represent the fraction of the potential that is actually felt by the enzymes in the membrane.

Calcium handling

We include the two major mitochondrial calcium transporters, i.e., the Ca²⁺ uniporter and the Na⁺/Ca²⁺ exchanger, in our model. The Ca²⁺ uniporter, which injects cytosolic Ca²⁺ into the mitochondria, and depends on the intracellular Ca²⁺ concentration (Ca_i) and the inner membrane potential, was modeled by Magnus and Keizer (23,25) as

$${\tilde{J}}_{\text{uni}}=J_{\text{max},\text{uni}}\frac{\frac{C{a}_{\text{i}}}{K_{\text{trans}}}{\left(1+\frac{C{a}_{\text{i}}}{K_{\text{trans}}}\right)}^3\frac{2F\left(\Delta \Psi -\Delta {\Psi }^o\right)}{RT}}{\left[{\left(1+\frac{C{a}_{\text{i}}}{K_{\text{trans}}}\right)}^4+\frac{L}{{\left(1+\frac{C{a}_{\text{i}}}{K_{\text{act}}}\right)}^{n_{\text{a}}}}\right]\left(1-e^{\frac{-2F\left(\Delta \Psi -\Delta {\Psi }^o\right)}{RT}}\right)},$$

where J_max,uni = 8.33 μM/ms, K_trans = 16 μM, and F/RT = 0.037/mV is Faraday's constant divided by the gas constant and temperature, ΔΨ^o = 91mV, L = 50, K_act = 0.38 μM, and n_a = 2.8. We approximate ${\tilde{J}}_{\text{uni}}$ in our model with the simpler form

$$J_{\text{uni}}=p_{16}C{a}_{\text{i}}^2{e}^{p_{17}\Delta \Psi }\text{.}$$ (27)

Fig. S1 in the Supporting Material illustrates the uniporter Ca²⁺-transport rate, as calculated by the two models.

The Ca²⁺ efflux through the Na⁺/Ca²⁺ exchanger was modeled by Magnus and Keizer (23,25) as

$${\tilde{J}}_{\text{NaCa}}=J_{\text{max},\text{NaCa}}\frac{e^{\frac{bF\left(\Delta \Psi -\Delta {\Psi }^o\right)}{RT}}}{{\left(1+\frac{K_{\text{Na}}}{N{a}_{\text{i}}}\right)}^n\left(1+\frac{K_{\text{Ca}}}{C{a}_{\text{m}}}\right)},$$

where J_max,NaCa = 0.3694 μM/ms, b = 0.5, K_Na = 9.4 mM, Na_i = 30 mM, n = 3, and K_Ca = 3.75 μM. We approximate ${\tilde{J}}_{\text{NaCa}}$ in our model with the simpler form

$$J_{\text{NaCa}}=\frac{p_{18}C{a}_{\text{m}}}{p_{19}+C{a}_{\text{m}}}{e}^{p_{20}\Delta \Psi }\text{.}$$ (28)

Fig. S2 illustrates the Na⁺/Ca²⁺-exchanger rate, as calculated by the two models.

Reducing equivalents

On the basis of stoichiometry and a quasi-steady-state glucose-metabolism assumption, Magnus and Keizer (25) modeled the rate at which glycolytic end-products are made available to mitochondria as

$${\tilde{J}}_{\text{gly}}=\frac{{\mathit{\beta }}_{\text{max}}\left(1+{\mathit{\beta }}_{1}Glu\right){\mathit{\beta }}_{2}GluAT{P}_{\text{i}}}{1+{\mathit{\beta }}_{3}AT{P}_{\text{i}}+\left(1+{\mathit{\beta }}_{4}AT{P}_{\text{i}}\right){\mathit{\beta }}_{5}Glu+\left(1+{\mathit{\beta }}_{6}AT{P}_{\text{i}}\right){\mathit{\beta }}_{7}Gl{u}^2},$$

where β_max = 2.625 μM/ms/mM, β₁ = 1.66/mM, β₂ = 0.0249/mM, β₃ = 4/mM, β₄ = 2.83/mM, β₅ = 1.3/mM, β₆ = 2.66/mM, and β₇ = 0.16/mM². Glu is the plasma-glucose concentration (mM) and ATP_i is the intracellular ATP concentration (mM). β_max includes a cytosol/mitochondria volume ratio factor (1/0.09), so that the flux is in terms of mitochondrial volume. As the ${\tilde{J}}_{\text{gly}}$ dependence on ATP_i is extremely weak, we neglect it by setting ATP_i = 1.8 mM, which is in the middle of the physiological range (25). We then approximate the glucose-availability rate in our model with the simpler form

$$J_{\text{gly}}=p_{21}{\left(\frac{Glu}{1\text{mM}}\right)}^{1/2}\text{.}$$ (29)

Modified forms of the Magnus and Keizer (25) glucose-dependent NADH_m and FADH_2,m production rates are given by

$$\begin{array}{c}{\tilde{J}}_{\text{N},\text{Glu}}=8f\left(C{a}_{\text{m}}\right){\tilde{J}}_{\text{gly}},\\ {\tilde{J}}_{\text{F},\text{Glu}}=4f\left(C{a}_{\text{m}}\right){\tilde{J}}_{\text{gly}},\end{array}$$

respectively, where

$$f\left(C{a}_{\text{m}}\right)=\frac{1}{1+u_2\left[1+u_1{\left(1+\frac{C{a}_{\text{m}}}{K_{{\text{Ca}}_{\text{m}}}}\right)}^{-2}\right]},$$

and where u₁ = 15, u₂ = 1.1 and $k_{{\text{Ca}}_{\text{m}}}$ = 0.05 μM. We approximate ${\tilde{J}}_{\text{N},\text{Glu}}$ and ${\tilde{J}}_{\text{F},\text{Glu}}$ in our model as

$$J_{\text{N},\text{Glu}}=8p_{22}{J}_{\text{gly}}\left(\frac{C{a}_{\text{m}}}{p_{23}+C{a}_{\text{m}}}\right),$$ (30)

$$J_{\text{F},\text{Glu}}=4p_{22}{J}_{\text{gly}}\left(\frac{C{a}_{\text{m}}}{p_{23}+C{a}_{\text{m}}}\right),$$ (31)

respectively. Fig. S3 illustrates the NADH_m production rate computed by the two models. J_F,Glu has the same qualitative behavior.

Electron transport chain

The rate of oxidation of NADH_m that results in the consumption of a single oxygen atom to produce H₂O was modeled by Magnus and Keizer (23) as

$${\tilde{J}}_{\text{O},\text{N}}=0.5{\mathit{\rho }}_{\text{res},\text{N}}\frac{\left(r_{\text{a}}{10}^{6\Delta pH}+r_{\text{c}1}{e}^{\frac{6F\Delta {\Psi }_{\text{B}}}{RT}}\right)e^{\frac{F{A}_{\text{res},\text{N}}}{RT}}-r_{\text{a}}{e}^{\frac{6g_{1}F\Delta \Psi }{RT}}+r_{\text{c}2}{e}^{\frac{F{A}_{\text{res},\text{N}}}{RT}}{e}^{\frac{6g_{1}F\Delta \Psi }{RT}}}{\left(1+r_1{e}^{\frac{F{A}_{\text{res},\text{N}}}{RT}}\right)e^{\frac{6F\Delta {\Psi }_{\text{B}}}{RT}}+\left(r_2+r_3{e}^{\frac{F{A}_{\text{res},\text{N}}}{RT}}\right)e^{\frac{6g_{1}F\Delta \Psi }{RT}}},$$

where

$$A_{\text{res},\text{N}}=\frac{RT}{F}\ln \left(K_{\text{res},\text{N}}{\left(\frac{NAD{H}_{\text{m}}}{NA{D}_{\text{m}}}\right)}^{1/2}\right),$$

and where ρ_res,N = 500 μM, r_a = 6.394 × 10⁻¹³/ms, ΔpH = –0.4, ΔΨ_B = 50 mV,g₁ = 0.97, r_c1 = 2.656 × 10⁻²²/ms, r_c2 = 8.632 × 10⁻³⁰/ms, r₁ = 2.077 × 10⁻¹⁸, r₂ = 1.728 × 10⁻⁹, r₃ = 1.059 × 10⁻²⁶, and K_res,N = 1.35 × 10¹⁸. The value g₁ was adjusted from its original value of 0.85 in Magnus and Keizer (23) to better agree with experimental observations of the ΔΨ-dependence of the proton efflux rate, J_H⁺, _efflux, shown in Fig. 4. We approximate ${\tilde{J}}_{\text{O},\text{N}}$ in our model with the simpler form

$$J_{\text{O},\text{N}}=p_1{\left(\frac{NAD{H}_{\text{m}}}{NA{D}_{\text{m}}}\right)}^{1/2}\left(\frac{1}{1+e^{\left(\Delta \Psi -p_2\right)/p_3}}\right)\text{.}$$ (32)

Fig. S4 illustrates the H₂O production rate that results from NADH_m oxidation, as calculated by the two models. Using a factor of six that corresponds to the ideal H⁺:e^– ratio, we approximate the proton efflux rate resulting from this H₂O production as (23)

$$J_{\text{Hres},\text{N}}=12J_{\text{O},\text{N}},$$ (33)

which has the same qualitative behavior as J_O,N (Fig. S4). Note that the oxidation rate of NADH_m resulting in H₂O production decreases as ΔΨ increases, illustrating metabolic control as it becomes more difficult to pump protons against a large potential (16).

Similar to that of NADH_m, the rate of reduction of a single oxygen atom from the oxidation of FADH_2,m can be modeled as (23,24)

$${\tilde{J}}_{\text{O},\text{F}}=0.5{\mathit{\rho }}_{\text{res},\text{F}}\frac{\left(r_{\text{a}}{10}^{4\Delta pH}+r_{\text{c}1}{e}^{\frac{4F\Delta {\Psi }_{\text{B}}}{RT}}\right)e^{\frac{F{A}_{\text{res},\text{F}}}{RT}}-r_{\text{a}}{e}^{\frac{4g_{1}F\Delta \Psi }{RT}}+r_{\text{c}2}{e}^{\frac{F{A}_{\text{res},\text{F}}}{RT}}{e}^{\frac{4g_{1}F\Delta \Psi }{RT}}}{\left(1+r_1{e}^{\frac{F{A}_{\text{res},\text{F}}}{RT}}\right)e^{\frac{4F\Delta {\Psi }_{\text{B}}}{RT}}+\left(r_2+r_3{e}^{\frac{F{A}_{\text{res},\text{F}}}{RT}}\right)e^{\frac{4g_{1}F\Delta \Psi }{RT}}},$$

where

$$A_{\text{res},\text{F}}=\frac{RT}{F}\ln \left(K_{\text{res},\text{F}}{\left(\frac{FAD{H}_{2,\text{m}}}{FA{D}_{\text{m}}}\right)}^{1/2}\right),$$

and where ρ_res,F = 1250 μM and K_res,F = 5.765 × 10¹³. We approximate ${\tilde{J}}_{\text{O},\text{F}}$ in our model with the simpler form

$$J_{\text{O},\text{F}}=p_4{\left(\frac{FAD{H}_{2,\text{m}}}{FA{D}_{\text{m}}}\right)}^{1/2}\left(\frac{1}{1+e^{\left(\Delta \Psi -p_2\right)/p_3}}\right)\text{.}$$ (34)

Using a factor of four that corresponds to the ideal H⁺:e^– ratio, we approximate the corresponding proton efflux rate as (23)

$$J_{\text{Hres},\text{F}}=8J_{\text{O},\text{F}},$$ (35)

where J_O,F and J_Hres,F have the same qualitative behavior as J_O,N (Fig. S4).

ATP production

One turn of the TCA cycle results in the production of one GTP molecule, which we assume is converted immediately to an ATP molecule by the nucleotide diphosphate kinase. We approximate the glucose-dependent rate of ATP production from the TCA cycle in our model as (25)

$$J_{\text{TCA},\text{Glu}}=2p_{22}{J}_{\text{gly}}\left(\frac{C{a}_{\text{m}}}{p_{23}+C{a}_{\text{m}}}\right),$$ (36)

which has the same qualitative behavior as J_N,Glu (Fig. S3).

ATP is also produced by the F₁F₀-ATP synthase, which harnesses the energy stored in ΔΨ. Magnus and Keizer (23) modeled the ATP production rate of this reaction as

$${\tilde{J}}_{\text{F1F0}}=-{\mathit{\rho }}_{\text{F1F0}}\frac{\left(d_{\text{a}}{10}^{3\Delta pH}+d_{\text{c}1}{e}^{\frac{3F\Delta {\Psi }_{\text{B}}}{RT}}\right)e^{\frac{F{A}_{\text{F1F0}}}{RT}}-d_{\text{a}}{e}^{\frac{3g_{2}F\Delta \Psi }{RT}}+d_{\text{c}2}{e}^{\frac{F{A}_{\text{F1F0}}}{RT}}{e}^{\frac{3g_{2}F\Delta \Psi }{RT}}}{\left(1+d_1{e}^{\frac{F{A}_{\text{F1F0}}}{RT}}\right)e^{\frac{3F\Delta {\Psi }_{\text{B}}}{RT}}+\left(d_2+d_3{e}^{\frac{F{A}_{\text{F1F0}}}{RT}}\right)e^{\frac{3g_{2}F\Delta \Psi }{RT}}},$$

where

$$A_{\text{F1F0}}=\frac{RT}{F}\ln \left(\frac{K_{\text{F1F0}}AT{P}_{\text{m}}}{0.8AD{P}_{\text{m}}P{i}_{\text{m}}}\right),$$

and where ρ_F1F0 = 1800 μM from Bertram et al. (16) and Cortassa et al. (24), g₂ = 1.07, d_a = 1.656 × 10⁻⁸/ms, d_c1 = 9.651 × 10⁻¹⁷/ms, d_c2 = 4.845 × 10⁻²²/ms, d₁ = 1.346 × 10⁻⁸, d₂ = 7.739 × 10⁻⁷, d₃ = 6.65 × 10⁻¹⁵, K_F1F0 = 1.71 × 10⁶ mM, and Pi_m = 20 mM. The value g₂ was used here to shift the inflection point of the ΔΨ-dependent curve to lower ΔΨ in agreement with the shifts made in ${\tilde{J}}_{\text{O},\text{N}}$ and ${\tilde{J}}_{\text{O},\text{F}}$ above. We approximate ${\tilde{J}}_{\text{F1F0}}$ in our model with the simpler form

$$J_{\text{F1F0}}=\frac{p_{24}AD{P}_{\text{m}}}{AD{P}_{\text{m}}+p_{25}AT{P}_{\text{m}}}\left(\frac{1}{1+e^{\left(p_{26}-\Delta \Psi \right)/p_{27}}}\right)\text{.}$$ (37)

Fig. S5 illustrates the ATP production rate from the F₁F₀-ATP synthase, as calculated by the two models. Using a factor of three that corresponds to the ideal H⁺:P_i ratio, we approximate the proton influx through the F₁F₀-ATP synthase as

$$J_{\text{H},\text{ATP}}=3J_{\text{F}1\text{F}0},$$ (38)

which has the same qualitative behavior as J_F1F0 (Fig. S5).

The rate of ATP transport out of the mitochondrial matrix through the ANT exchanger was modeled by Magnus and Keizer (23) as

$${\tilde{J}}_{\text{ANT}}=J_{\text{max},\text{ANT}}\frac{1-\frac{a_{1}AT{P}_{\text{i}}AD{P}_{\text{m}}}{AD{P}_{\text{i}}AT{P}_{\text{m}}}{e}^{\frac{-F\Delta \Psi }{RT}}}{\left(1+\frac{a_{2}AT{P}_{\text{i}}}{AD{P}_{\text{i}}}{e}^{\frac{-fF\Delta \Psi }{RT}}\right)\left(1+\frac{a_{3}AD{P}_{\text{m}}}{AT{P}_{\text{m}}}\right)},$$

where J_max,ANT = 20.8 μM/ms, a₁ = 0.8, a₂ = 0.11, f = 0.5, and a₃ = 7.2. The value ADP_i is the intracellular ADP concentration (mM). To simplify this expression, we assume the intracellular and mitochondrial matrix nucleotide ratios are maintained at approximately equal values by the transporter (16), i.e., ATP_i/ADP_i ≈ ATP_m/ADP_m, so that

$${\tilde{J}}_{\text{ANT}}\approx J_{\text{max},\text{ANT}}\frac{1-a_1{e}^{\frac{-F\Delta \Psi }{RT}}}{\left(1+\frac{a_{2}AT{P}_{\text{m}}}{AD{P}_{\text{m}}}{e}^{\frac{-fF\Delta \Psi }{RT}}\right)\left(1+\frac{a_{3}AD{P}_{\text{m}}}{AT{P}_{\text{m}}}\right)}\text{.}$$

We approximate ${\tilde{J}}_{\text{ANT}}$ in our model with the simpler form

$$J_{\text{ANT}}=\frac{p_{28}AT{P}_{\text{m}}}{AD{P}_{\text{m}}+p_{29}AT{P}_{\text{m}}}{e}^{p_{30}\Delta \Psi }\text{.}$$ (39)

Fig. S6 illustrates the ANT exchange rate, as calculated by the two models.