Abstract
We investigated for the first time the genetic and environmental aetiology behind scientific achievement in primary school children, with a special focus on possible aetiological differences for boys and girls. For a representative community sample of 2,602 twin pairs assessed at age nine years, scientific achievement in school was rated by teachers based on National Curriculum criteria in three domains: Scientific Enquiry, Life Processes, and Physical Processes. Results indicate that genetic influences account for over 60% of the variance in scientific achievement, with environmental influences accounting for the remaining variance. Environmental influences were mainly of the non-shared variety, suggesting that children from the same family experience school environments differently. An analysis of sex differences considering differences in means, variances, and aetiology of individual differences found only differences in variance between the sexes, with boys showing greater variance in performance than girls.
Introduction
Science became a compulsory subject in primary teaching in the United Kingdom in 1989 with the introduction of the National Curriculum (NC). Much genetic research into academic performance has focused on other core subjects, particularly reading, and more recently mathematics (Oliver et al., 2004; Walker, Petrill, Spinath, & Plomin, 2004). The genetic and environmental aetiology of science performance in school has not previously been investigated. Information about the development of scientific ability in school is relevant to a society that places great importance on the study and application of science and technology.
Science in primary school is a very broad subject, made up of many domains, which might in part explain the lack of genetically sensitive research into this subject. In addition, the skills that contribute to academic performance in science are not known, such as mathematical, linguistic, or general learning skills. It is timely to investigate the relative influences of nature and nurture on the development of scientific performance in the early school years and to explore whether these genetic and environmental influences differ between the sexes.
Sex Differences and Individual Differences
Comments from the former Harvard President Lawrence Summers, in January 2005, reignited a long-standing debate in America on the intrinsic abilities of females in science. Could there be genetic and environmental differences that differentially influence the performance of males and females in science? And are these differences present in early science development in primary school?
Previous publications in this journal have considered the existence of sex differences in science; for example, differences in attitudes towards science between the sexes (Miller, Slawinski Blessing, & Schwartz, 2006) and sex-related differences in science and mathematics course choice (van Langen, Rekers-Mombarg, & Dekkers, 2006). In addition, a recent review has claimed that the under-representation of women in scientific careers is not due to sex differences in aptitude for science (Spelke, 2005) and there is increasing support for the Gender Similarities Hypothesis (Hyde, 2005). The Gender Similarities Hypotheses, based on meta-analyses of gender differences studies from childhood and adulthood, states that males and females are much more alike than is generally portrayed. In fact, effect sizes for the influence of gender on cognitive variables are close to zero.
These analyses have generally focused on mean differences between the sexes. It may be more informative, in an increasingly personalised society, to consider why individuals differ, not just how and why groups differ. Such research might eventually enable educationalists to develop more effective intervention strategies for the pupils in their classrooms. The causes behind differences in means and individual differences are not necessarily the same. For example, an average difference between males and females could be largely environmental in origin but individual differences could be largely genetic. In the case of science performance, groups of boys and girls might differ in performance because of differences in exposure to scientific concepts (mean differences). However, the reasons for differences in performance within those groups (i.e., the influences on individual performance rather than group performance) may be genetic. Much work in psychology aims to explain what makes people the same, whereas work in individual differences is more interested in what makes people different. There is a need for research that can consider the aetiology behind individual differences in science performance, and whether the aetiology of these differences is the same for males and females. The twin method has often been used as a rough screen of the aetiology behind such individual differences in performance (see, e.g., Martin, Boomsma, & Machin, 1997; Plomin, DeFries, McClearn, & McGuffin, in press; Rijsdijk & Sham, 2002).
The Twin Method
One of the major methods used in quantitative genetics to estimate genetic and environmental influences is the twin method. This design allows researchers to investigate the causes or influences that affect phenotypes (i.e., their aetiology). Twinning provides naturally occurring quasi-experimental comparisons. To estimate both genetic and environmental parameters of individual differences, the twin method requires both identical twins (monozygotic [MZ]) and non-identical twins (dizygotic [DZ]). MZ twins are 100% genetically similar, whereas DZ twins are on average only 50% similar for segregating genes. At a crude level this means that if a trait is influenced by genetics, then within-pair resemblance for that trait should be higher in MZ twins than in DZ twins.
There are two types of DZ twins: same-sex (DZss) and opposite-sex (DZos). Most twin studies focus on DZss because they provide a more appropriate comparison to MZ twins, who are always of the same sex. However, as discussed later, DZos make it possible to assess sex differences in twin analyses.
The prevalence of each type of twins is roughly one-third, so approximately 33% of twins born will be MZ, 33% DZss and 33% DZos.
Assumptions of the Twin Method
The twin method is based on two main assumptions. The first assumption is that MZ twins and DZ twins will have equally similar environments; this is one of the benefits of studying DZ twins and not just ordinary siblings. This assumption, termed the “equal environments assumption” (Evans & Martin, 2000), means that greater MZ similarity is attributed to genetic influence; but if it is the case that MZ twins experience more similar environments than DZ twins, then this greater similarity may be due to environmental influences and not genetic influences. Much research has tested the equal environments assumption (Bouchard, Jr. & Propping, 1993) and, although there is overwhelming evidence to suggest that MZ twins are treated more similarly (Scarr, 1968), this differential treatment does not significantly affect twin similarity for behaviours such as personality and cognitive abilities (Morris-Yates, Andrews, Howie, & Henderson, 1990). In fact it appears that it is the similarity of the MZ twins that results in a more similar parental response (Lytton, 1977); this is evidence for genetics driving environmental influences (Plomin & Bergeman, 1991). If the environment is genetically influenced, then this is not a violation of the equal environments assumption as the differences between MZ and DZ twins have not been originally caused by an environmental effect.
The second assumption of the twin method is that results from twin studies can be generalised to the rest of the population. Specifically, the twin method assumes that twins are similar to singletons. There are many ways in which twins have been found to differ from singletons (Evans & Martin, 2000); for example, twins on average have lower birth weights and are often born 3–4 weeks prematurely (Plomin et al., in press). Some studies have found that twins have lower IQ scores when compared with singletons (Record, McKeown, & Edwards, 1970), with triplets showing even lower IQ scores than twins. However, those studies that have found differences between twins and singletons have been conducted on young twins, and studies on older twins confirm that these differences have all but disappeared by early to middle childhood (Evans & Martin, 2000).
The twin method, based on these assumptions and the genetic relatedness of twins, allows us to estimate the relative influences of nature and nurture on a particular trait, in a particular population at a specific time.
Twin Research into Other Academic Abilities
Previous studies into other academic abilities may be relevant because they yield a surprising but consistent pattern of results. Performance in schools seems to be moderately influenced by genetics and minimally influenced by shared environments, environmental influences that make children growing up together in the same family similar (Plomin & Kovas, 2005).
Results for teacher-reported mathematics and English abilities consistently yield moderate heritabilities, and low shared environmental influences (Oliver et al., 2004; Walker et al., 2004). Similar results have been obtained for reading tests and mathematics tests (Harlaar, Dale, & Plomin, 2005; Kovas, Petrill, & Plomin, 2007). It seems that genetics and non-shared environmental influences are mainly at play in producing the wide array of individual differences in academic abilities. However, twin research into reading comprehension of Social Science and Natural Science based passages (Loehlin & Nichols, 1976) shows a somewhat different pattern, with estimates differing to some extent between the sexes, with females showing greater shared environmental estimates and lower heritability. Therefore, despite the consistency of results for English and mathematics, we cannot be sure that the same is true for science performance.
Current Study
We investigated for the first time the genetic and environmental origins of teacher reported science performance, based on NC standards, using a large and representative cohort of twins aged nine years. In addition, we have considered three types of sex differences in science performance: mean differences, variance differences, and individual differences. Based on the Gender Similarities Hypothesis (Hyde, 2005), we expected to find no mean or variance differences in science performance. Using same-sex and opposite-sex twins, we investigated the extent to which genetic and environmental influences differ for boys and girls; that is, whether the aetiology of individual differences in science performance differed between the sexes. We predicted that the genetic and environmental origins of individual differences in science performance are similar for boys and girls. Based on previous findings concerning the aetiology of other academic skills, we expected to find that individual differences in science performance are moderately influenced by genetics and have minimal influence of shared environment.
Method
Sample
The sampling frame for the present study was the Twins’ Early Development Study (TEDS), a study of twins born in England and Wales in 1994, 1995, and 1996 (Trouton, Spinath, & Plomin, 2002). The TEDS sample has been shown to be reasonably representative of the general population in terms of parental education, ethnicity, and employment status (see Oliver & Plomin, 2007; Trouton et al., 2002).
Using the TEDS sample, 4,077 families from the 1994 and 1995 cohorts who participated at age seven years consented to participate in the nine-year assessments. These 4,077 families are representative of the total TEDS sample and the general population. Of these 4,077 families, 3,859 families (95%) agreed to participate in the teacher assessments, allowed us to contact the current teachers of the twins, and provided school details. Teachers were contacted when the children were towards the end of their fourth year of primary school so that the teachers would be familiar with the children’s performance during the school year. Teachers were sent a covering letter with the background and aims of TEDS, as well as explaining that we had obtained consent from the twins’ parents to ask teachers for information about the child’s performance at school. Teacher forms for both members of a twin pair were distributed at the same time. When the same teacher assessed both twins in a pair, responses for the twins were received simultaneously; when different teachers assessed members of a twin pair, responses were usually received within a few days of each other, although some pairs were assessed a few weeks apart. In this sample, 63% of the twins were rated by the same teacher. There was no bias toward MZ twins being kept together in the same classroom: 63% of MZ twins versus 62% of DZ twins had the same teacher. Previous studies have shown that a teacher who has both twins in the classroom rates them more similar than two teachers rating each child in a twin pair (Walker et al., 2004). However, this effect is the same regardless of whether the twins are identical or non-identical, and therefore the estimate of genetic influence remains constant. This pattern of results was also evident in this sample, so analyses are not reported separately by rating from the same or different teachers.
As expected, the correlations between the date of the teacher questionnaire being returned and the science scores were low (−0.013 to 0.004), indicating negligible effects of time of teacher assessment. Teachers were asked to check one of five boxes to indicate level of attainment in terms of the NC criteria (see Measures). Data were collected for this study between 2003 and 2005, based on the current NC criteria that included three strands of science performance: scientific enquiry, life processes, and physical processes. Of the teacher questionnaires sent for the nine-year testing, 5,836 individual forms (76%) were returned complete. For the purposes of the current study, we excluded 530 individuals from the nine-year assessment if at least one member of the twin pair had a specific medical syndrome or was an extreme outlier for perinatal problems such as extreme low birth weight. Further to this, we excluded those families where we received a questionnaire for only one member of the twin pair.
The number of pairs for each measure, split by sex and zygosity, can be found later in Table 3. The mean age of the twins when questionnaires were returned from the teachers was 9.04 years (range = 8.46–10.54 years). We repeated the analyses using different exclusion criteria and our findings remained unchanged; we therefore do not report these results separately.
Table 3.
Intraclass Correlations for Three Science Measures and the Composite for Twins by Zygosity and Sex
| Measure | MZ | DZ | DZss | DZos | MZM | MZF | DZM | DZF |
|---|---|---|---|---|---|---|---|---|
| Scientific Enquiry | 0.72 (n = 910) | 0.44 (n = 1616) | 0.44 (n = 837) | 0.45 (n = 779) | 0.71 (n = 408) | 0.73 (n = 502) | 0.41 (n = 399) | 0.47 (n = 438) |
| Life Processes | 0.73 (n = 901) | 0.43 (n = 1599) | 0.42 (n = 832) | 0.43 (n = 767) | 0.74 (n = 403) | 0.72 (n = 498) | 0.41 (n = 394) | 0.43 (n = 438) |
| Physical Processes | 0.72 (n = 893) | 0.43 (n = 1585) | 0.45 (n = 822) | 0.41 (n = 763) | 0.73 (n = 402) | 0.72 (n = 491) | 0.45 (n = 391) | 0.45 (n = 431) |
| Science Composite | 0.77 (n = 913) | 0.46 (n = 1624) | 0.46 (n = 843) | 0.45 (n = 781) | 0.76 (n = 410) | 0.77 (n = 503) | 0.45 (n = 402) | 0.47 (n = 441) |
Note. MZ = monozygotic; DZ = dizygotic same and opposite-sex twins; DZss = dizygotic same-sex twins; DZos = dizygotic opposite-sex twins; MZM = monozygotic male twins; MZF = monozygotic female twins; DZM = dizygotic male twins; DZF = dizygotic female twins; n = number of complete twin pairs.
All correlations were significant at p < .01.
Zygosity was assessed through a parent questionnaire of physical similarity, which has been shown to be over 95% accurate when compared with DNA testing (Price et al., 2000). For cases where zygosity was unclear from this questionnaire, DNA testing was conducted.
Measures
As for all children, the twins’ scientific performance was assessed throughout the fourth year of school by their teachers, using the assessment materials of the NC for England and Wales, the core academic curriculum developed by the Qualifications and Curriculum Authority (QCA). Assessment at the end of Key Stages involves two types of measurement, NC Direct Testing and NC Teacher Assessments (TA). The TA consist of teachers giving a score from a five-point scale on the basis of the child’s performance throughout the school year. In the current study, the TA at Key Stage 2 were used, which are familiar to teachers and are designed for children age 8 through their sixth year of primary school at age 11. At the time of testing, the QCA provided teachers with NC material and assessment guidelines for three strands of science for Key Stage 2, which directly map on to areas in science that are taught throughout the NC at this stage: Scientific Enquiry; Life Processes; and Physical Processes. At age 9 we do not assess Materials and Properties, but this will be assessed when the twins are 12 years old. (See online for the five-point NC criteria given by the QCA and used by teachers to indicate achievement levels in each of the areas of science: http://www.ncaction.org.uk/subjects/science/levels.htm (National Curriculum in Action, 2006).) Along with the NC Direct Test score, the TA score given by the teacher on these NC criteria for a particular child ultimately determines the final score that is submitted to the QCA for that child at the end of the Key Stage.
For the purposes of the present study, teachers were asked to check one of five boxes to indicate the child’s TA score. Reminders of the NC criteria used to select the appropriate attainment level were provided as part of the questionnaire. Further details about these measures have been published previously (Walker et al., 2004). Similar to other measures used in the behavioural sciences, this is an ordinal rather than interval scale—but it is better than most ordinal Likert scales in that it attempts to specify behavioural criteria at each level rather than merely indicating performance relative to an unspecified average performance. Teachers are familiar with the use of these criteria because they follow the NC for England and Wales; in addition, we provide a reminder of the level descriptions with the questionnaire.
It should be emphasised that the present study is limited to the TA, which are the teachers’ perceptions of science performance. In addition, the teacher report is an ordinal scale rather than an interval scale. Although it would have been desirable to include objective tests as well as these year-long teacher assessments, within the NC there is no formal testing of science until Year 6 (age 11 years) and we were unable to include a direct test for this large sample. There is evidence for the validity of teacher assessments. In a meta-analysis of 16 international studies comparing teacher assessments and standardised test results, a median correlation of 0.66 was found despite great variations in the methods used for teacher assessments (Hoge & Coladarci, 1989; see Oliver et al. [2004] and Walker et al. [2004] for further support of the use of teacher assessments). Moreover, similar TA of Reading in our study correlate highly (0.68) with a telephone-administered test of word and non-word reading (Dale, Harlaar, & Plomin, 2005), and that TA of overall academic achievement correlates highly (0.58) with telephone-administered tests of verbal and nonverbal cognitive abilities (Spinath, Walker, Saudino, & Plomin, in press).
The use of teacher assessments of science performance as indicated by the TA is a strength as well as a limitation of our study, since there is some evidence to support the hypothesis that teacher assessments add to achievement tests in predicting longterm outcomes. For example, after controlling for socio-economic status, preschool teachers’ overestimates and underestimates of intelligence relative to IQ scores at the age of four significantly predicted high school grades and Scholastic Aptitude Test results 14 years later (Alvidrez & Weinstein, 1999). A similar study of teacher assessments of underachieving students predicts long-term educational attainment and career outcomes (McCall, Evahn, & Kratzer, 1992).
The three TA measures (Scientific Enquiry, Life Processes, and Physical Processes) were standardised to a mean of zero and a standard deviation of one on the basis of the entire sample of twins (with children with major perinatal and medical problems excluded as described earlier), and provided the basis for our analysis. The three scales and composite scores were normally distributed, and the maximum and minimum scores did not exceed 3.5 standard deviations above or below the mean. The three scales are highly correlated, with an average intercorrelation of
0.83. A factor analysis of the three scales indicated that the principal component accounted for 88% of the variance. We therefore computed a composite science score by calculating a mean from the standardised scores and re-standardising this composite score. Preliminary results will include all three measures and the composite measure; but, due to the high intercorrelations between the science subscales, advanced analyses were only conducted for the composite measure, as the subscales appear to be assessing the same domain.
Twins are perfectly correlated for age, and same-sex twins are correlated perfectly for sex, therefore any variation due to age or sex could contribute to the correlation between twins (Eaves, Eysenck, & Martin, 1989). Data uncorrected for age and sex would inflate twin correlations. For this reason, and as is standard in twin analysis, all measures were corrected for age and sex effects using a regression procedure (McGue & Bouchard, Jr., 1984).
The Twin Method
An individual’s phenotype is made up of genetic and environmental influences (Plomin et al., in press), which is the sum of additive genetic effects (i.e., those genetic effects that sum up to influence a phenotype), non-additive genetic effects (i.e., those genetic effects that interact to influence a phenotype), and environmental effects. Generally the twin method focuses on additive genetic effects. Non-additive genetic effects can also be modelled; non-additive genetic effects would be indicated if the MZ twin intra-class correlation is more than twice the DZ twin intra-class correlation. By comparing the twin intra-class correlations, it is possible to estimate additive genetic effects, shared environmental effects (i.e., environmental effects that make children in the same family more similar), and non-shared environmental effects (i.e., environmental effects that make children growing up in the same family different). These three effects are commonly known as A, C, and E, respectively: “A” is a genetic effect size known as heritability, and can be estimated by doubling the difference between MZ and DZ twin correlations—so, for example, if the correlations are .80 and .50, respectively, then heritability, or A, is estimated as 60% (0.6). The shared environmental influence is the variance that makes MZ and DZ twins similar, but is not explained by additive genetic effects. It is estimated by subtracting the estimate of heritability from the MZ correlation. Therefore, in the above example, the C component would be estimated as 20% (0.2). In addition, non-shared environmental influences can be estimated from the total variance not shared by MZ twins; non-shared environmental influences are the only influence deemed to make MZ twins different. Therefore, in the above example, the E component would be estimated as 20% (0.2) (i.e., 1 – .80). The total variance explained cannot exceed 1 (or 100%) (Plomin et al., in press). The non-shared environment component (E) also includes measurement error.
A more elegant way of estimating the ACE parameters is maximum likelihood model fitting analysis (Plomin et al., in press), which provides more detailed estimates of genetic and environmental effect sizes that make assumptions explicit, tests the fit of the entire model to the data, tests the relative fit of alternative models, and provides confidence intervals for the parameter estimates. A discussion of the use of maximum likelihood model fitting analyses can be found elsewhere (Neale, Boker, Xie, & Maes, 1999; Neale & Maes, in press; Plomin et al., in press; Rijsdijk & Sham, 2002).
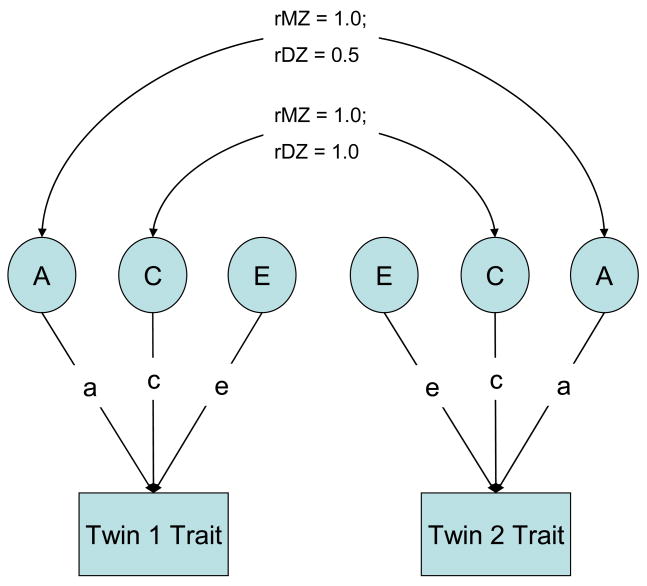
A path diagram of the basic twin model is shown in Figure 1. In path diagrams, the rectangular boxes refer to observed phenotypes, and the circles represent latent genetic and environmental factors; the single-headed arrows represent partial regressions of the variable on the latent factor (i.e., the relative influence of the latent variable [e.g., A] on the phenotype), and finally the curved connectors represent correlations between the connected factors (Saudino, Ronald, & Plomin, 2005). The path coefficients of latent variables A (additive genetic), C (shared environmental), and E (non-shared environmental, including error of measurement) factors are represented by the lower-case letters a, c, and e, respectively. Path coefficients indicate the relative importance of the latent variable on the trait; for example, the relative influence of the A (additive genetic) variable on science performance. Genetic relatedness or the genetic correlation (rG) is 1.0 for MZ twins and 0.5 for DZ twins (i.e., MZ twins are 100% genetically similar and DZ twins are only 50% similar for segregating genes). Environmental relatedness or the shared environmental correlation (rC) is assumed to be 1.0 both for MZ and DZ twins (i.e., the equal environments assumption). The full ACE model dissects the phenotypic variance into these three components of variance.
Figure 1.
Basic Twin Model
Note: A = additive genetic influence; C = shared environment influence; E = non-shared environment influence; path coefficients a, c, and e = effects of A, C, and E on a trait; rMZ = monozygotic correlation; rDZ = dizygotic correlation. Figure shows the path diagram that represents both the scalar model and the null model. The scalar and null models of the sex-limitation design reduce to the basic twin model shown here. This model estimates three parameters: a, c, and e for the sexes combined. In the scalar model, variance differences between the sexes are allowed. In the null model, the variances are equated across the sexes (this is not shown in the path diagram).
Analyses
Analysis of variance (ANOVA) was used to analyse sex differences in means and variances. Most of the analyses focus on the more novel aetiological analysis of individual differences and sex differences in these aetiologies using the classical twin method. As described, the proportion of the variance for a particular trait that is attributable to additive genetic influences, and shared and non-shared environmental influences, can be estimated from twin analyses.
To investigate sex differences, twin intra-class correlations were calculated separately for the five zygosity groups: MZ males, MZ females, DZ males, DZ females, and DZ opposite-sex twins. The typical Pearson correlation is an inter-class correlation in the sense that it indexes the covariance between two distinct classes of variables. In contrast, in twin studies that correlate members of a twin pair, there are no obvious classes and the goal is to describe covariance for all possible pairings of the twins. The intra-class correlation is used for this purpose, which indexes the proportion of total variance that is between-pairs (Shrout & Fleiss, 1979). The inclusion of male and female MZ and DZ twins as well as DZ opposite-sex twins permits the analysis of both “quantitative” and “qualitative” sex differences (Neale & Cardon, 1992; Neale et al., 1999). Quantitative sex differences refer to sex differences in the magnitude of genetic and environmental influences; for example, comparing the magnitude of the difference between MZ male and DZ male twin intra-class correlations with the difference between MZ female and DZ female twin intra-class correlations. For genetic influences, quantitative differences would mean that genetic effects influence the trait to different extents in males and females. In contrast, qualitative sex differences refer to different genetic and environmental effects for males and females, which is implied if the intra-class correlation for opposite- sex twins is significantly less than the correlation for the same-sex DZ twins. For genetic influences, qualitative differences would mean that there are different genetic influences for the trait for males and females. If genetic and environmental influences are different for males and females, this will reduce the within-pair similarity in the opposite-sex pairs (Harlaar, Spinath, Dale, & Plomin, 2005). In addition, it is possible to test for variance differences between males and females in the context of these models.
In this study, model-fitting was explicitly used to test for the presence of sex differences in aetiology. The relative fit of models allowing different types of sex differences and no sex differences are compared to assess which model best describes the data. Mx software for structural equation modelling was used to perform standard model-fitting analyses using raw data (Neale et al., 1999). Two fit indices are reported: chi-square (X2), and Akaike’s information criterion (Akaike, 1987). The best-fitting model was chosen on the basis of a change in X2 not representing a significant worsening of fit; for a change of degrees of freedom (df) of 1, the statistically significant change in X2 is 3.84. Fit statistics are compared with a saturated phenotypic model, which models the observed means and variances without attributing them to additive genetic, shared environmental, and non-shared environmental factors. Therefore, this comparison is a test of whether the variance can be partitioned into genetic and environmental influences.
In the current paper, for the composite science score, we performed model-fitting analyses, using a full sex-limitation model. The full sex-limitation model tests for three sex differences: quantitative, qualitative, and variance differences between the sexes. For further details about this model, see the Appendix. This model has been widely used in other studies (Eley, 2005; Galsworthy, Dionne, Dale, & Plomin, 2000; Jacobson, Prescott, & Kendler, 2002).
Results
The means and standard deviations (SD) for the three science scores and for the composite at age 9 years are presented in Table 1. Males have slightly greater means and variances than females on all of the science scores. The results of a 2 × 2 (sex by zygosity) ANOVA, shown in Table 2, indicate no significant effects of sex on any of the four scores despite the large sample size, which provides 90% power to detect mean differences as small as 0.1SD (i.e., d = 0.1), accounting for just 0.2% of the variance (Cohen, 1988). We report η2 as a measure of effect size. There were significant main effects of zygosity on three of the four science scores (Science:Scientific Enquiry, p = .003, η2 = 0.002; Science:Life Processes, p = .002, η2 = 0.002; Science:Physical Processes, p = .060, η2 = 0.001; Science:Composite, p = .005, η2 = 0.002), although these significant effects are attributable to the large sample size because the effect size was very small, accounting for less than 1% of the variance. There was also a significant interaction between sex and zygosity for two of the four science measures (Science:Scientific Enquiry, p = .037, η2 = 0.001; Science:Life Processes, p = .195, η2 < 0.001; Science:Physical Processes, p = .033, η2 = 0.001; Science:Composite: p = .051, η2 = 0.001), but again the effect sizes of these significant effects are very small, accounting for less than 1% of the variance.
Table 1.
Means (and standard deviations) for 9-Year Teacher Assessments of Science (Adjusted for Age), by zygosity and sex
| Zygosity | Sex | ||||
|---|---|---|---|---|---|
| Measure | All | MZ | DZ | Male | Female |
| Scientific Enquiry | 0.01 (1.00) | −0.04 (.99) | 0.04 (1.00) | 0.04 (1.04) | −0.01 (.95) |
| n = 5107 | n = 1843 | n = 3264 | n = 2416 | n = 2691 | |
| Life Processes | 0.01 (1.00) | −0.04 (.99) | 0.04 (1.00) | 0.02 (1.05) | 0.01 (.94) |
| n = 5075 | n = 1832 | n = 3243 | n = 2397 | n = 2678 | |
| Physical Processes | 0.01 (.99) | −0.02 (.97) | 0.03 (1.00) | 0.04 (1.04) | −0.01 (.95) |
| n = 5048 | n = 1822 | n = 3226 | n = 2390 | n = 2658 | |
| Composite | 0.01 (.99) | −0.03 (.98) | 0.04 (1.00) | 0.03 (1.05) | −0.01 (.94) |
| n = 5119 | n = 1846 | n = 3273 | n = 2421 | n = 2698 | |
Note. Each score was adjusted for age and standardized on the basis of the whole sample (after medical exclusions). MZ = monozygotic twins; DZ = dizygotic twins. N value is number of individuals; therefore these n values differ slightly to those in table 3, which represent complete paired data for twins.
Genetic Analysis of Individual Differences
The twin intra-class correlations for the four scores are presented in Table 3. They are presented for the total group of MZ, DZ same-sex, and DZ opposite-sex as well as for the male and female subgroups among the same-sex pairs. In every case, MZ correlations exceeded those of the DZ twins, suggesting genetic influence. For the entire sample, doubling the difference between the MZ and the DZ same-sex correlations to estimate heritability indicates that genetics substantially, and consistently, influences Science scores for Scientific Enquiry (.56), Life Processes (.60), Physical Processes (.58), and for the Composite Science score (.62). Estimates of the shared environment—subtracting the above estimates of heritability from the MZ twin correlation—were consistently modest for the three measured scales (average .14).
Across zygosity, correlations between male and female pairs were quite similar, yielding reasonably similar estimates for heritability and shared environment. For example, for the science composite score, the correlations for males and females were .76 and .77, respectively, for MZ twins, and were .45 and .47 for same-sex DZ twins. Estimates of heritability and shared environment are very similar for males and females (.62 and .14, respectively, for males, and .60 and .17 for females). The sex-limitation model presented in the following section tested whether these quantitative sex differences between males and females are significant.
Correlations for opposite-sex DZ twins (average = .43) were similar to those for same-sex DZ twins (average = .44) on the three measured scales. These results suggest that there are no qualitative sex differences.
The results of model-fitting analyses are presented in Table 4. The likelihood ratio chi-squared tests identified the scalar model as the best-fitting model. The scalar model is the most parsimonious model that does not produce a significant worsening of fit (judged by change in X2). This model allows variance differences between the sexes, but not qualitative or quantitative sex differences (i.e., estimates for opposite-sex twins do not differ from estimates for same-sex twins, and estimates for males and females are the same). The model-fitting estimates of heritability and shared environment for boys and girls are similar to those estimated from the twin correlations (see Table 3). In general, the ACE model-fitting results indicate substantial heritability and modest shared environmental influence, as suggested by the twin correlations in Table 3. Estimates from the best-fitting scalar model are .62 and .14, respectively, with non-shared environment accounting for the remaining variance.
Table 4.
Fit Indices and Parameter Estimates from the Full-Sex Limitation Model and Sub-models Fit to Science Composite Score
| Model | Δχ2 | Δdf | AIC | Δχ2 | Δdf | p | Male | Female | rG | rC | s2m | s2f | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a2m | c2m | e2m | a2f | c2f | e2f | |||||||||||
| Full (rG free) | 7.255 | 7 | −6.745 | - | - | - | 0.62 (.47–.73) | 0.14 (.04–.28) | 0.24 (.21–.28) | 0.62 (.49–.74) | 0.15 (.05–.28) | 0.23 (.20–.26) | 0.50 | 1.00 | 1.06 | 0.95 |
| Full (rC free) | 7.255 | 7 | −6.745 | - | - | - | 0.62 (.47–.73) | 0.14 (.04–.28) | 0.24 (.21–.28) | 0.62 (.49–.74) | 0.15 (.05–.28) | 0.23 (.20–.26) | 0.50 | 1.00 | 1.06 | 0.95 |
| Common effects | 7.255 | 8 | −8.745 | 0.000 | 1 | 0.988 | 0.62 (.48–.73) | 0.14 (.04–.28) | 0.24 (.21–.28) | 0.62 (.49–.74) | 0.15 (.05–.28) | 0.23 (.20–.26) | 0.50 | 1.00 | 1.06 | 0.95 |
| a2 | c2 | e2 | ||||||||||||||
| Scalar | 7.567 | 10 | −12.433 | 0.312 | 3 | 0.958 | 0.62 (.54–.71) | 0.14 (.07–.22) | 0.23 (.21–.25) | 0.50 | 1.00 | 1.06 | 0.95 | |||
| Null model | 42.209 | 11 | 20.209 | 34.953 | 4 | 0.000 | 0.63 (.55–.71) | 0.14 (.06–.21) | 0.23 (.21–.25) | 0.50 | 1.00 | 1.00 | 1.00 | |||
Note. Δχ2 = change in chi-squared firstly in comparison to the fully saturated model and then in comparison to the full sex-limitation model; Δdf = change in degrees of freedom between comparison models; p = significance level comparing reduced models to the full model; a2m, c2m, e2m = additive genetic, shared environmental and non-shared environmental estimates for males; a2f, c2f, e2f = additive genetic, shared environmental and non-shared environmental estimates for females; rG = genetic correlation for opposite-sex DZ twins; rC = shared environmental correlation for opposite-sex twins; s2m = predicted variance in males, s2f = predicted variance in females. See text for a description of the model.
Discussion
The aim of this study was to investigate the genetic and environmental aetiology behind scientific performance in schools, using a large, representative community sample of nine-year-old twins, and to explore possible sex differences. Results support our hypotheses: Science performance, as rated by teachers, is substantially heritable (.62) and shows only modest shared environmental influence (.14). There were no significant qualitative or quantitative sex differences, suggesting that boys and girls are influenced by the same genetic/environmental effects (no qualitative differences) and that the extent of that influence is similar across the sexes (no quantitative differences). Despite the large sample, there were no significant mean differences between the sexes; there were significant but slight variance differences, with males showing greater variances than females.
The implications of finding substantial genetic influence and only modest influence of the shared environment are more relevant to the level of educational policy than to individual teachers. These findings will not be of help to a teacher confronted with a particular child who is struggling with science. However, it may be useful at a practical level for teachers to recognise that differences among children in their science performance are not just due to differences in effort because genetic sources of differences are also important. The current study’s evidence for strong genetic influence might become more practical as specific genes are identified that account for this heritability. For example, identifying genes might make it possible to predict children’s patterns of genetic strengths and weaknesses, and to intervene to prevent problems before they occur.
Environmental Influences
The twin method is a valuable tool not only for investigating genetic influences, but also for identifying the nature of environmental influences. Environmental influences are classified as shared influences that make the twins more similar, and nonshared influences that contribute to differences between the twins. Just as important as the genetic results is the environmental finding that for science performance in schools there is so little shared-environmental influence (.14) when the twins are living in the same home and going to the same school, with 63% of the twins being taught by the same teacher. However, the nature of non-shared environmental effects means that school and home environments are not unimportant, but that the twins experience these environments differently. The finding of the importance of non-shared environment is consistent with the theory that environmental influences operate on an individual-by-individual basis and not generally on a family-by-family basis (Plomin, Asbury, & Dunn, 2001). Familial influence is largely genetic in origin.
In relation to science performance, such non-shared environmental influences may also arise from within-twin differences in motivation and interest in science. Research has shown that children’s enthusiasm for science progressively declines during the primary school years (Murphy & Beggs, 2003; Pell & Jarvis, 2001). Reasons suggested for this decline in interest include a lack of practical work in science, non-specialist teaching, and overemphasis on practice assessments for national tests (Murphy & Beggs, 2003). Also, government initiatives in numeracy and literacy have resulted in changes to the timetabling that can result in only short afternoon sessions for science, when there may not be time to perform practical work (Murphy, Ambusaidi, & Beggs, 2006).
Sex Differences
The best-fitting model was the scalar model, which does not allow quantitative or qualitative sex differences but does allow variance differences. From the estimates of the full model and the common effects model, and also from the twin intra-class correlations, there are small differences between male and female estimates of heritability.
However, these differences are not nearly significant, with both male and female estimates falling well within each other’s 95% confidence intervals. Also, the results from the ANOVA show that there is no main effect of sex, and, although there is a significant interaction between sex and zygosity, it explains virtually no variance at all, and is only significant because of our very large sample size. The fact that the null model is a significantly worse fit suggests that there are significant variance differences, although the differences in male and female variances are very small (s2m = 1.06, s2f = 0.95).
Therefore, the results suggest that, across the distribution, boys and girls do not have different influences affecting their science performance. In addition, there are no mean differences in performance between males and females, and only slightly greater variance in scores for males compared with females. However, later on in life there is still an under-representation of women in scientific careers (Spelke, 2005). It is not impossible that genetic and environmental influences change throughout development, and therefore this cannot be ruled out. Alternatively, the differential representation of the sexes in scientific careers may be more influenced by society and adverse environmental factors that impact on women in science, such as the difficulties in returning to research after an extended career break (see, e.g., ASSET, 2003). Only future research throughout development and later life will allow these issues to be investigated.
Limitations
An apparent limitation of this study is the use of teacher-report data rather than objectively measured science performance. However, such teacher reports are an important part of the NC and may actually represent a more coherent observation of the child’s ability in science over the course of a year. A major emphasis in primary science is to foster scientific enquiry and reasoning; such skills may be difficult to assess in formal testing. Moreover, much of the previous work on academic abilities has focused on teacher-report data, and correlations between objective test data and teacher-reports are generally high (see, e.g., Harlaar, Date et al., 2005).
Reports have suggested that primary school teachers lack confidence in their knowledge of the science curriculum (see, e.g., Murphy et al., 2006), which is a possible limitation of this study. However, results from our concurrent studies concerning teacher report data of other academic abilities show highly comparable findings, suggesting that any possible insecurities that teachers may have about science education do not seem to be influencing their ratings of children’s performancein science as compared with other academic subjects.
As discussed earlier, although the twin method in general has its limitations, research into the assumptions of the twin method have consistently found that the assumptions are reasonable and, for this reason, the twin method has been used throughout the medical sciences as a rough estimate of the influence of nature and nurture (Martin et al., 1997).
It might also be considered a limitation that we are using the twin method as a rough guide to the relative influence of nature and nurture rather than conducting molecular genetic research to identify specific differences in DNA sequence that are responsible for heritable differences between individuals. However, it is expensive and difficult to identify even some of the many DNA differences likely to be responsible for any common disorders or complex traits (Plomin, Kennedy, & Craig, 2006). Therefore it is reasonable to investigate aetiology within a quantitative genetic design, and then to use this information to inform the design of molecular genetic studies. For instance, given that the three components of science performance are so highly correlated, it would make sense to investigate a general science factor in molecular genetic research. Moreover, unlike molecular genetic research, which is limited to addressing genetics, the twin method provides as much information about the environment as it does about genetics. In the present study, finding so little shared environmental influence is at least as important as finding so much genetic influence.
Future Directions
Now that we have verified that science performance shows similar genetic and environmental estimate patterns to other academic subjects, such as reading (Harlaar, Hayiou-Thomas, & Plomin, 2005) and mathematics (Kovas et al., 2007; Oliver et al., 2004), it would be of interest to investigate the aetiological links between science and other academic abilities, and also with general cognitive ability. In contrast to the univariate model-fitting analyses of science performance in the present paper, the relationships between science performance and other academic subjects can be assessed by multivariate genetic analyses that address the covariance between traits rather than the variance of each trait considered separately (Neale & Maes, 2001; Neale et al., 1999). Such an analysis should also ideally be conducted at different ages, particularly when general science is split into biology, chemistry, and physics in secondary school. Primary science may show different aetiological links in multivariate analyses from those of science in secondary schools. For example, it may be that science in primary schools is more genetically and environmentally correlated to English performance than to mathematics performance, whereas later in schooling the opposite may be true. Multivariate genetic designs will allow the aetiology of these relationships to be investigated.
Further to this, it is important to monitor the genetic and environmental influences on science throughout development using both teacher-report data and objective test data. Are the same genetic and environmental influences present at different stages of development, or do genetic effects contribute to continuity across ages and environmental effects contribute to change (Plomin, 1986)? There is certainly a long way to go towards understanding what skills contribute to science performance in primary school, and how individual children develop their scientific skills and understanding.
Mathematics and English have been studied throughout the distribution of abilities, and especially at the low end of the distribution in terms of disabilities or impairments. However, no research has considered “science disability”, which opens up an entirely new area for research. In terms of genetic research, it cannot be assumed that the same genetic and environmental influences that operate throughout the normal distribution of academic performance in science are also responsible for children who have special problems in science education, or for those children at the high extreme of the distribution. We plan to capitalise on the size of the present twin sample to investigate genetic and environmental influences on academic performance in science to study the low and high ends of the distribution.
Table 2.
ANOVA Results Showing Significance and Effect Size for Teacher Assessments for Three Science Measures and the Composite, by Sex and Zygosity
| Science Measures | Sex | Zygosity | Sex*zygosity |
|---|---|---|---|
| Scientific Enquiry | p = 0.247 | p = 0.003 | p = 0.037 |
| η2 < 0.001 | η2 = 0.002 | η2 = 0.001 | |
| Life Processes | p = 0.873 | p = 0.002 | p = 0.195 |
| η2 < 0.001 | η2 = 0.002 | η2 < 0.001 | |
| Physical Processes | p = 0.210 | p = 0.060 | p = 0.033 |
| η2 < 0.001 | η2 = 0.001 | η2 = 0.001 | |
| Composite | p = 0.426 | p = 0.005 | p = 0.051 |
| η2 < 0.001 | η2 = 0.002 | η2 = 0.001 |
Note: η2 = eta squared (effect size).
Acknowledgments
We gratefully acknowledge the ongoing contribution of the parents and children in the Twins’ Early Development Study (TEDS). TEDS is supported by a programme grant (G0500079) from the UK Medical Research Council; our work on school environments and academic achievement is supported by grants from the US National Institutes of Health (HD44454 and HD46167, respectively).
Appendix. Sex-limitation model
In the current paper, for the composite science score, we performed model-fitting analyses, using a full sex-limitation model. The full sex-limitation model tests for three sex differences: quantitative, qualitative and variance differences between the sexes. To test for the different types of sex difference it is necessary to first test a full sex-limitation model and then three nested models, which progressively model fewer parameters.
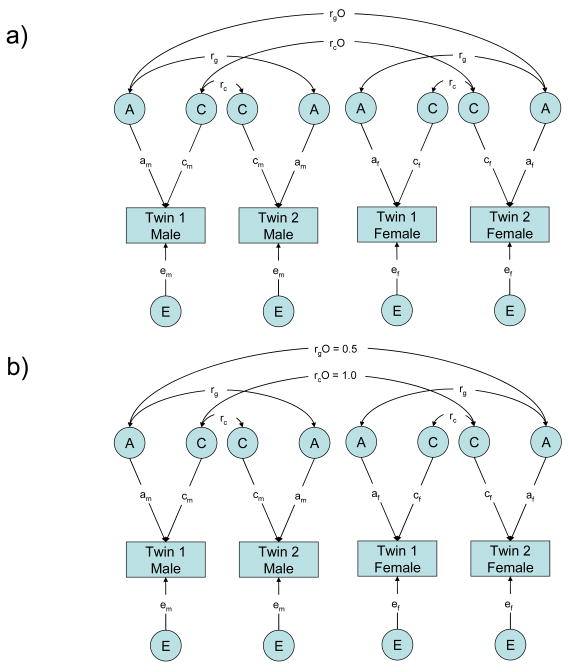
Figure 2 shows a path diagram of a full sex-limitation model and subsequent nested models. This model incorporates the five zygosity-by-sex groups. For the same-sex pairs, the model is the same as the basic univariate twin model, but males and females are modelled separately and have specific male and female path coefficients (am, cm, em and af, cf, ef). The model for the fifth group, the opposite-sex twins, is incorporated in this full model and is represented by Twin 1 Male and Twin 2 Female. Correspondingly, the rGO and rCO labels link these twins and refer to the genetic and shared environment correlations between opposite-sex twins, respectively. In a basic univariate model the genetic and shared environment correlations (rG and rC) are fixed at 1.0 and 1.0 for MZ twins and 0.5 and 1.0 for DZ twins. In the sex-limitation model for the opposite-sex twins these variables are allowed to be ‘free’, that is allowed to vary from 0.5 and 1.0, to allow the estimation of qualitative sex differences. If there are qualitative sex differences the genetic correlation for opposite-sex twins will be less than 0.5 or the shared environment correlation will be less than 1.0.
Figure 2.
Full Sex-Limitation Model and Nested Models
Full sex-limitation model and nested models. Note: A = additive genetic influence; C = shared environment influence; E = non-shared environment influence; path coefficients a, c, and e = effects of A, C, and E on a trait, with subscript “m” for males and “f” for females; rg = genetic correlation between same-sex twins, which is fixed at 1.0 for MZ twins and 0.5 for DZ twins; rc = shared environment correlation between same-sex twins, which is fixed at 1.0 for MZ and DZ twins; rgO = genetic correlation between opposite-sex twins; rcO = shared environment correlation between opposite-sex twins. Opposite-sex twins are represented as twin 1 male and twin 2 female, and are linked by rgO and rcO. (a) Full sex limitation model. This model estimates seven parameters: am, cm, em, af, cf, ef, and rgO or rcO. This model allows qualitative sex differences by allowing the genetic and shared environmental correlations (rgO and rcO) between opposite-sex twins to vary. The model also allows quantitative sex differences by allowing the ACE parameters for males and females (am, cm, em, af, cf, ef) to differ. Variances differences between the sexes are allowed (this cannot be seen in the path diagram). (b) Common effects model, which is nested in the full sex-limitation model. The common effects model constrains the genetic and shared environmental correlations between opposite-sex twins (rgO and rcO) to be 0.5 and 1.0, respectively (thereby treating the opposite-sex twins in the same way as the same-sex DZ twins who have a genetic correlation of 0.5 and a shared environmental correlation of 1.0). This model estimates six parameters (am, cm, em, af, cf, ef) and allows variance differences between the sexes. Please see Figure 1 for the path diagram of the scalar and null models.
The first model to be fitted to the data is the full sex-limitation model (see Figure 2 part a). This model estimates all seven parameters (am, cm, em, af, cf, ef and rGO or rCO). The fit of this model is then compared to the other models to assess which model best describes the data. This full sex-limitation model allows for quantitative (by looking at male and female estimates separately), qualitative (by allowing the rGO and rCO to vary for opposite sex twins) and variance sex differences.
The first nested model to be tested is the common effects model, which allows quantitative sex differences, but not qualitative sex differences (see Figure 2 part b). This model constrains the opposite-sex twins’ rGO to equal 0.5 and rCO to equal 1.0, but allows the ACE parameters for males and females to differ. Therefore, the difference in fit between this model and the full sex-limitation model indicates the extent to which there are qualitative sex differences in science achievement.
The second nested model to be tested is the scalar model, which allows only phenotypic variance differences between the sexes, and does not allow for qualitative or quantitative sex differences (see Figure 1—the scalar model reduces to the basic twin model shown in Figure 1). Therefore in the scalar model the opposite-sex twins’ rGO must equal 0.5 and rCO must equal 1.0, and ACE parameters for males and females are equated. The difference in fit between this model and the common effects model indicates the extent to which there are quantitative sex differences.
The final model tested is the null model, which reduces to the basic twin model (shown in Figure 1) because it constrains the opposite-sex twins’ rGO to 0.5 and rCO to 1.0, equates ACE parameters for males and females, and also equates phenotypic variance for males and females (i.e. it tests the null hypothesis that there are no sex differences.) The relative fit of this model to the scalar model indicates whether there are any variance differences for males and females. Therefore by comparing the relative fits of the models to the previous model and to the full model it is possible to ascertain whether there are a) quantitative sex differences, b) qualitative sex differences, c) variance differences or d) no differences between males and females. It is theoretically possible that all three types of differences occur in a particular sample, which would mean that the model of best fit would be the full sex-limitation model. However, the sample size must be extremely large in order to have sufficient power to reliably detect all of these differences simultaneously. (see Eley, 2005; Galsworthy et al., 2000; Neale et al., 1999; Neale et al., 2001; Plomin et al., in press for further information about the use of sex limitation models for twin data).
References
- Akaike H. Factor analysis and AIC. Psychometrika. 1987;52:317–332. [Google Scholar]
- Alvidrez J, Weinstein RS. Early teacher perceptions and later student academic achievement. Journal of Educational Psychology. 1999;91:731–746. [Google Scholar]
- ASSET. The Athena survery of science engineering and technology in higher education. Norwich, UK: UEA; 2003. (Report No. 26) [Google Scholar]
- Bouchard TJ, Jr, Propping P. Twins as a tool of behavioral genetics. Chichester, UK: John Wiley & Sons; 1993. [Google Scholar]
- Cohen J. Statistical power analysis for the behavioral sciences. 2. Hillsdale, NJ: Lawrence Erlbaum Associates; 1988. [Google Scholar]
- Dale P, Harlaar N, Plomin R. Telephone testing and teacher assessment of reading skills in 7-year-olds: I. Substantial correspondence for a sample of 5808 children and for extremes. Reading and Writing: An Interdisciplinary Journal. 2005;18:385–400. [Google Scholar]
- Eaves LJ, Eysenck H, Martin NG. Genes, culture, and personality: An empirical approach. London: Academic Press; 1989. [Google Scholar]
- Eley TC. Sex-limitation models. In: Everitt BJ, Howell D, editors. Encyclopedia of Behavioural Statistics. West Sussex, UK: Wiley; 2005. [Google Scholar]
- Evans LJ, Martin NG. The validity of twin studies. Genescreen. 2000;1:77–79. [Google Scholar]
- Galsworthy MJ, Dionne G, Dale PS, Plomin R. Sex differences in early verbal and non-verbal cognitive development. Developmental Science. 2000;3:206–215. [Google Scholar]
- Harlaar N, Dale PS, Plomin R. Telephone testing and teacher assessment of reading skills in 7-year-olds: II. Strong genetic overlap. Reading and Writing: An Interdisciplinary Journal. 2005;18:401–423. [Google Scholar]
- Harlaar N, Hayiou-Thomas ME, Plomin R. Reading and general cognitive ability: A multivariate analysis of 7-year-old twins. Scientific Studies of Reading. 2005;9:197–218. [Google Scholar]
- Harlaar N, Spinath FM, Dale P, Plomin R. Genetic influences on early word recognition abilities and disabilities: A study of 7-year-old twins. Journal of Child Psychology and Psychiatry. 2005;46:373–384. doi: 10.1111/j.1469-7610.2004.00358.x. [DOI] [PubMed] [Google Scholar]
- Hoge RD, Coladarci T. Teacher-based judgments of academic achievement: A review of literature. Review of Educational Research. 1989;59:297–313. [Google Scholar]
- Hyde JS. The Gender Similarities Hypothesis. American Psychologist. 2005;60:581–592. doi: 10.1037/0003-066X.60.6.581. [DOI] [PubMed] [Google Scholar]
- Jacobson KC, Prescott CA, Kendler KS. Sex differences in the genetic and environmental influences on the development of antisocial behavior. Development & Psychopathology. 2002;14:395–416. doi: 10.1017/s0954579402002110. [DOI] [PubMed] [Google Scholar]
- Kovas Y, Petrill SA, Plomin R. The origins of diverse domains of mathematics: Generalist genes but specialist environments. Journal of Educational Psychology. 2007;99(1):128–139. doi: 10.1037/0022-0663.99.1.128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loehlin JC, Nichols J. Heredity, environment and personality. Austin, TX: University of Texas; 1976. [Google Scholar]
- Lytton H. Do parents create or respond to differences in twins? Developmental Psychology. 1977;13:456–459. [Google Scholar]
- Martin N, Boomsma DI, Machin G. A twin-pronged attack on complex trait. Nature Genetics. 1997;17:387–392. [Google Scholar]
- McCall RB, Evahn C, Kratzer L. High school underachievers: What do they achieve as adults? Pittsburgh, PA: Sage; 1992. [Google Scholar]
- McGue M, Bouchard TJ., Jr Adjustment of twin data for the effects of age and sex. Behavior Genetics. 1984;14:325–343. doi: 10.1007/BF01080045. [DOI] [PubMed] [Google Scholar]
- Miller PH, Slawinski Blessing J, Schwartz S. Gender differences in high-school students’ views about science. International Journal of Science Education. 2006;28:363–381. [Google Scholar]
- Morris-Yates A, Andrews G, Howie P, Henderson S. Twins: A test of the equal environments assumption. Acta Psychiatrica Scandinavica. 1990;81:322–326. doi: 10.1111/j.1600-0447.1990.tb05457.x. [DOI] [PubMed] [Google Scholar]
- Murphy C, Ambusaidi A, Beggs J. Middle East meets West: Comparing children’s attitudes to school science. International Journal of Science Education. 2006;28:405–422. [Google Scholar]
- Murphy C, Beggs J. Children’s perceptions of school science. School Science Review. 2003;84:109–116. [Google Scholar]
- National Curriculum in Action. Science level descriptions. 2006 Retrieved October 5, 2006, from: http://www.ncaction.org.uk/subjects/science/levels.htm.
- Neale MC, Boker SM, Xie G, Maes H. Mx: Statistical modeling. 5. Richmond, VA: Department of Psychiatry, Virginia Commonwealth University; 1999. [Google Scholar]
- Neale MC, Cardon LR. Methodology for genetic studies of twins and families. Dordrecht, The Netherlands: Kluwer Academic Publications; 1992. [Google Scholar]
- Neale MC, Maes HM. Methodology for genetic studies of twins and families. Dordrecht, The Netherlands: Kluwer Academic Publishers B.V; 2001. [Google Scholar]
- Oliver B, Harlaar N, Hayiou-Thomas ME, Kovas Y, Walker SO, Petrill SA, et al. A twin study of teacher-reported mathematics performance and low performance in 7-year-olds. Journal of Educational Psychology. 2004;96:504–517. [Google Scholar]
- Oliver BR, Plomin R. Twins Early Development Study (TEDS): A multivariate, longitudinal genetic investigation of language, cognition and behavior problems from childhood through adolescence. Twin Research and Human Genetics. 2007;10:96–105. doi: 10.1375/twin.10.1.96. [DOI] [PubMed] [Google Scholar]
- Pell T, Jarvis T. Developing attitude to science scales for use with children of ages from five to eleven years. International Journal of Science Education. 2001;23:847–862. [Google Scholar]
- Plomin R. Development, genetics, and psychology. Hillsdale, NJ: Erlbaum; 1986. [Google Scholar]
- Plomin R, Asbury K, Dunn J. Why are children in the same family so different? Nonshared environment a decade later. Canadian Journal of Psychiatry. 2001;46:225–233. doi: 10.1177/070674370104600302. [DOI] [PubMed] [Google Scholar]
- Plomin R, Bergeman CS. The nature of nurture: Genetic influences on “environmental” measures. Behavioral and Brain Sciences. 1991;14:373–427. [Google Scholar]
- Plomin R, DeFries JC, McClearn GE, McGuffin P. Behavioral genetics. 5. New York: Worth Publishers; in press. [Google Scholar]
- Plomin R, Kennedy JKJ, Craig IW. The quest for quantitative trait loci associated with intelligence. Intelligence. 2006;34:513–526. [Google Scholar]
- Plomin R, Kovas Y. Generalist genes and learning disabilities. Psychological Bulletin. 2005:592–617. doi: 10.1037/0033-2909.131.4.592. [DOI] [PubMed] [Google Scholar]
- Price TS, Freeman B, Craig IW, Petrill SA, Ebersole L, Plomin R. Infant zygosity can be assigned by parental report questionnaire data. Twin Research. 2000;3:129–133. doi: 10.1375/136905200320565391. [DOI] [PubMed] [Google Scholar]
- Record RG, McKeown T, Edwards JH. An investigation of the differences in measured intelligence between twins and single births. Annal of Human Genetics. 1970:11–20. doi: 10.1111/j.1469-1809.1970.tb00215.x. [DOI] [PubMed] [Google Scholar]
- Rijsdijk FV, Sham PC. Analytic approaches to twin data using structural equation models. Briefings in Bioinformatics. 2002;3:119–133. doi: 10.1093/bib/3.2.119. [DOI] [PubMed] [Google Scholar]
- Saudino KJ, Ronald A, Plomin R. Rater effects in the etiology of behavior problems in 7-year-old twins: Parent ratings and ratings by same and different teachers. Journal of Abnormal Child Psychology. 2005;33:113–130. doi: 10.1007/s10802-005-0939-7. [DOI] [PubMed] [Google Scholar]
- Scarr S. Environmental bias in twin studies. Eugenics Quarterly. 1968;15:34–40. doi: 10.1080/19485565.1968.9987750. [DOI] [PubMed] [Google Scholar]
- Shrout PE, Fleiss J. Intraclass correlations: Uses in assessing rater reliability. Psychological Bulletin. 1979;86:420–428. doi: 10.1037//0033-2909.86.2.420. [DOI] [PubMed] [Google Scholar]
- Spelke ES. Sex differences in intrinsic aptitude for mathematics and science? A critical review. American Psychologist. 2005;60:950–958. doi: 10.1037/0003-066X.60.9.950. [DOI] [PubMed] [Google Scholar]
- Spinath FM, Walker SO, Saudino KJ, Plomin R. To what extent is genetic influence on teacher-assessed academic achievement due to genetic influence on test-assessed general cognitive ability? A study of 1812 pairs of 7-year-old twins. Intelligence in press. [Google Scholar]
- Trouton A, Spinath FM, Plomin R. Twins Early Development Study (TEDS): A multivariate, longitudinal genetic investigation of language, cognition and behaviour problems in childhood. Twin Research. 2002;5:444–448. doi: 10.1375/136905202320906255. [DOI] [PubMed] [Google Scholar]
- van Langen A, Rekers-Mombarg L, Dekkers H. Sex-related differences in the determinants and process of science and mathematics choice in pre-university education. International Journal of Science Education. 2006;28:71–94. [Google Scholar]
- Walker SO, Petrill SA, Spinath FM, Plomin R. Nature, nurture and academic achievement: A twin study of teacher ratings of 7-year-olds. British Journal of Educational Psychology. 2004;74:323–342. doi: 10.1348/0007099041552387. [DOI] [PubMed] [Google Scholar]