Fast-time scale dynamics of Outer membrane protein A by extended model-free analysis of NMR relaxation data

Abstract

In order to better understand the dynamics of an integral membrane protein, backbone amide ¹⁵N NMR dynamics measurements of the β-barrel membrane protein OmpA have been performed at three magnetic fields. A total of nine relaxation data sets were globally analyzed using an extended model-free formalism. The diffusion tensor was found to be prolate axially symmetric with an axial ratio of 5.75, indicating a possible rotation of the protein within the micelle. The generalized order parameters gradually decreased from the mid-plane towards the two ends of the barrel, counteracting the dynamic gradient of the lipids in a matching bilayer, and were dramatically reduced in the extracellular loops. Large-scale internal motions on the ns time scale indicate that entire loops most likely undergo concerted (“sea anemone”-like) motions emanating from their anchoring points on the barrel. The case of OmpA in DPC micelles also illustrates inherent limitations of analyzing the data with even the most sophisticated current models of the model-free formalism. It is likely that conformational exchange processes on the ms-µs also play a role in describing the motions of some residues, but their analysis did not produce unique results that could be independently verified.

Introduction

OmpA is a two-domain structural protein of the outer-membrane of Gram-negative bacteria. It is believed to connect the outer membrane to the periplasmic peptidoglycan layer via its periplasmic domain. The β-barrel transmembrane (TM) domain of OmpA serves as a membrane anchor and also forms an ion channel in planar and spherical model membranes[1–4]. The structure of the TM domain of OmpA has been solved by x-ray crystallography[5, 6] and by NMR[7–9]. Although the crystal structure reveals several water-filled pockets in the core of the protein, there exists no continuous water-filled channel, but several luminal side-chains form a network of hydrogen-bonds and charge pairs in the core of the protein. A salt bridge formed by Glu52 and Arg138 across the center of the β-barrel appears to be the major obstruction or gate to ion conduction. Secondary partial obstructions are formed by a polar ring consisting of residues Lys12, Glu140, and Arg96 near the extracellular vestibule and a cover formed by the N-terminus on the periplasmic end of the pore. Molecular dynamics simulations have suggested alternative conformations of the residues forming the central gate and the periplasmic cover as a mechanism to open the OmpA channel to ion conduction[10]. More recently, the gating of the OmpA channel has been examined in more detail by double-mutant cycle analysis and single-channel measurements in planar lipid bilayers[11]. These results indicate that the closed-state strong (5.6 kcal/mol) salt bridge Glu52–Lys138 can be broken by forming the open-state intermediate strength (3.5 kcal/mol) salt bridge Glu52–Lys82 and a secondary weak (0.6 kcal/mol) salt bridge Arg138–Glu128.

Measurements of the amide ¹⁵N transverse and longitudinal nuclear spin relaxation rates and steady-state {¹H}-¹⁵N heteronuclear Overhauser effects (NOEs) are particularly useful in determining the dynamic behavior of the polypeptide backbone of proteins. These measurements are sensitive to dynamics on the ps-ns time scale, which may in turn contribute to the functions of proteins in various ways. Measurements of motions on this time scale permit thermodynamic samplings of conformational ensembles, a deeper understanding of the propagation long-range signal transduction within proteins, and thorough analyses of the allosteric regulation of ligand-binding through correlated motions[12]. To extract such fast time-scale dynamics, Lipari and Szabo developed a “model-free” approach, in which the internal motions and overall motions were assumed to be independent of one another[13, 14]. In this analysis, internal motions are described by the order parameter, S and the internal correlation time, τ_e. This approach was later extended to include internal motions on two different time-scales with a total of four parameters (fast and slow S and τ’s, respectively) describing the internal motions [15]. In order to accommodate the analysis of three relaxation data sets at a single magnetic field and to also include possible conformational exchange contributions on the ms-µs time-scale to the transverse relaxation rate, this extended model-free formalism has been simplified and reorganized to include up to three internal motion parameters[16]. Since then, this approach has been adopted very widely to explore the dynamics of many proteins on fast-time scales[12]. Taking advantage of nine data sets collected at three magnetic fields and globally fitting the data it is possible to reintroduce the full, extended model-free approach and to simultaneously also check for possible contributions of ms-µs conformational exchange. Here, we report an analysis of fast-time scale dynamics of OmpA in DPC micelles with the extended model-free formalism. We find that the backbone dynamic behavior of OmpA is quite complicated: its mobility decreases away from the center towards the two ends of the barrel, and many residues show internal motions on multiple time scales.

Materials and Methods

Protein sample preparation

The OmpA TM domain (residues 1–176) with a deleted signal sequence was overexpressed in BL21(DE3) cells and purified from inclusion bodies as described[7]. Cells were grown in minimal media in 99.9% D₂O containing 2g/L 98% ²H-, ¹³C-labeled D-glucose (MartekBio, Columbia, MD), 1g/L ¹⁵N-ammonium sulphate, and 1% DCN100 Bioexpress media (Cambridge Isotopes). The protein was refolded in DPC (D38, 98%) and concentrated on Amicon YM-1 membranes as described[7].

NMR spectroscopy

NMR spectra were recorded at 50 °C on Bruker DMX 750 MHz and 600 MHz spectrometers equipped with 5 mm triple-resonance probes and triple-axis or z-only field gradients, respectively, and 500 MHz spectrometer equipped with a 5 mm triple-resonance cryogenically-cooled probe with a z-axis pulsed field gradient. The ¹⁵N T₁ and T₂ relaxation data and the {¹H}-¹⁵N heteronuclear NOE data were recorded using three-dimensional TROSY-HNCO based sequences that incorporate standard techniques for measuring the dynamic parameters[17, 18]. The ¹⁵N T₁-TROSY-HNCO and ¹⁵N T₂-TROSY-HNCO data sets were recorded as series of 8–12 three-dimensional experiments with the parametric relaxation delays optimized for experiment type and field strength. For each real T₁ and T₂ increment 4–16 transients were co-added. Specifically, 500 MHz data were acquired with 4 transients and 12 relaxation delays (with the maximum parametric delays of 1.77 s for T₁ and 0.224 s for T₂); at 600 MHz 8 delays (the maximum parametric delays were 2.20 s for T₁ and 0.112 for T₂) and 16 transients were used, and the 750 MHz data sets each consisted of eight 3D spectra (with maximum parametric delays of 1.56 s for T₁ and 0.064 for T₂) acquired with 16 transients. The data sets in each series were recorded in a pseudo-random order. Recovery delays between scans were between 1.5 and 2.5 s for T₁ and T₂ experiments. {¹H}-¹⁵N heteronuclear NOE experiments were acquired as two interleaved 3D spectra (NOE and reference spectra, respectively), with each transient followed by an 8 s delay to establish a steady-state situation before the next scan. In the NOE spectrum, saturation of ¹H was obtained by applying 120° ¹H pulses spaced by 5 ms during the last 7.8 s of the inter-scan delay.

Spectral processing of the 3D data sets was performed with Felix 98 (Accelrys). Signal intensities were extracted simultaneously from all the spectra in each series of the fully processed 3D data sets by the program CHIFIT, using its pseudo-4D data processing mode[19]. The ¹⁵N T₁ and T₂ relaxation times were determined by a weighted nonlinear least-squares fit of a two-parameter, mono-exponential decay function of the measured signal intensities. The uncertainty of the extracted relaxation time parameter was derived from the variance-covariance matrix from each fit. The {¹H}-¹⁵N steady-state NOE value was determined as the ratio of the signal intensities obtained from the NOE and reference experiments, respectively. The uncertainties of the NOE values were estimated by error propagation using the error estimate for the signal intensities as reported by CHIFIT.

The TROSY version of CPMG relaxation dispersion experiments[20] were measured at ¹H field strength of 500 and 600 MHz. R_2,eff was calculated based on the equation[21]:

$$R_{2,\mathit{\text{eff}}}=-\frac{1}{T_{\mathit{\text{CP}}}}\text{ln}\frac{I({\nu }_{\mathit{\text{CPMG}}})}{I_0}$$

where I(ν_CPMG) and I₀ are peak intensities measured with and without the applied 80 ms constant time CPMG element, T_CP. Redundant measurements were performed to estimate standard deviations. Effective fields, ν_CPMG, as defined by 1/4τ_CPMG, ranged from 50 to 556 Hz, where 2τ_CPMG was the time between the centers of two consecutive 180° pulses. T_1ρ experiments were performed based on the established protocol[22] with improved pulse schemes[23].

Analysis of relaxation data

The analysis of ¹⁵N relaxation times and {¹H}-¹⁵N heteronuclear NOE values were performed in the context of the extended model-free formalism. Dominant contributions from the ¹H-¹⁵N dipole-dipole and the ¹⁵N CSA interactions were included[24], and if necessary, the conformational exchange contribution to the T₂ relaxation was modeled using the squared magnetic field dependence. In the model-free formalism, the overall diffusion model of the whole molecule is intertwined with internal model-free models of each residue in the molecule. The program “quadric_diffusion” (A. G. Palmer III, Columbia University) was applied to selected residues to determine the overall diffusion model for the molecule. This diffusion model was kept unchanged in all subsequent model-free analyses. The diffusion tensor parameters of this chosen model were used as initial inputs for model-free analysis using the program Relax[25, 26]. Model-free analysis in this program was achieved in an iterative fashion. One round of model-free analysis consisted of two separate steps. In step 1, up to ten different internal model-free models were applied and best-fitted to each residue in order to select the best internal model based on Akaike’s information criteria[25], while the overall diffusion tensor parameters were fixed. In step 2, the overall diffusion tensor parameters were optimized while the best-fitted individual internal model-free parameters for each residue were unchanged. These optimized overall diffusion model parameters were then fed as inputs for the next round of model-free analysis. Iteratively, convergence of all model-free parameters (both global diffusion and internal model-free parameters) was achieved when two successive rounds of fitting generated consistent outcomes. A ¹⁵N chemical shift anisotropy of –163 ppm and a N-H bond length of 1.04 Å were used in the program. The RDC-improved high-resolution solution NMR structure of OmpA (PDB code: 2GE4) was used to generate the anisotropic diffusion models[8].

Results

Measurement of NMR Dynamics

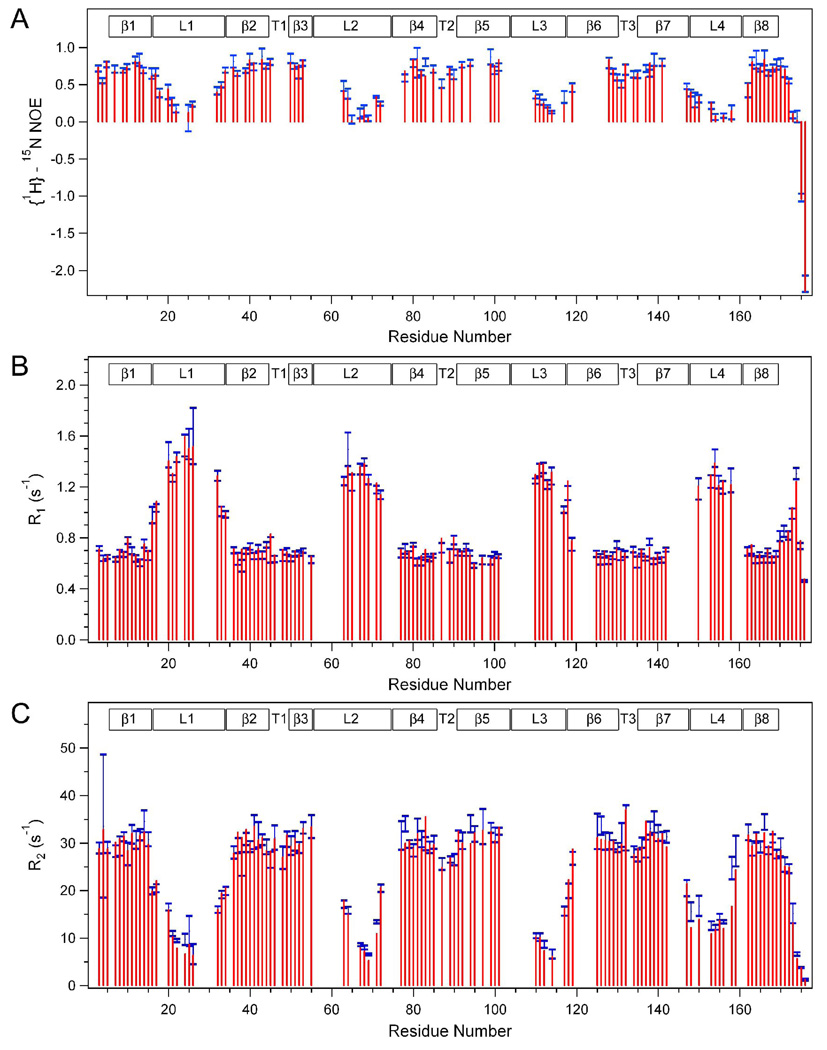
¹⁵N R₁ and R₂ relaxation rates and {¹H}-¹⁵N heteronuclear NOEs of the OmpA transmembrane domain were measured at three magnetic fields corresponding to ¹H frequencies of 750, 600, and 500 MHz. The center values of the blue bars in Figure 1 show the data measured at the 600 MHz, and the sizes of the bars indicate their standard deviations. The red bars represent the corresponding values back calculated from the best-fitted model-free analysis as explained below. Corresponding data recorded at 750 MHz and 500 MHz are displayed in Supplemental Figures S1 and Supplemental Figures S2, respectively. Residues in well-structured regions usually have relatively high heteronuclear NOE values, low R₁ relaxation rates, and high R₂ relaxation rates, whereas the opposite is true for more mobile residues. For instance, at 600 MHz, β-barrel and short periplasmic turn residues have average NOE, R₁, and R₂ values of 0.721, 0.686 s⁻¹, and 30.1 s⁻¹, respectively, whereas the less structured regions (C-terminus, and 4 extracellular loops) have average NOE, R₁, and R₂ values of 0.195, 1.21 s⁻¹ and 14.2 s⁻¹, respectively. Clearly, different regions of the protein display different dynamic behaviors: the loop and C-terminal residues are much more mobile than the β-barrel and turn residues. Similar results have been reported recently for an OmpA homolog from a different organism[27].

Figure 1.

Values of backbone amide heteronuclear {¹H}-¹⁵N NOEs (A) and ¹⁵N R₁s (B) and ¹⁵N R₂s (C) of the OmpA TM domain in DPC micelles recorded (blue bars, sizes indicate +/− standard deviations) and back-calculated (red bars) at 600 MHz and 50 °C. Regions of secondary structures are indicated on the top: β, β-strand; L, extracellular loop; T, periplasmic turn.

To probe for possible conformational exchange processes in the ms-µs range, relaxation dispersion experiments were performed[28]. However, neither T_1ρ nor CPMG experiments revealed definitive evidence for conformational exchange processes on time-scales accessible to these experiments for any of the observable residues. Because of this result, the subsequent primary model-free analysis was performed without the inclusion of conformational exchange parameters R_ex.

Global Diffusion Model

The program “quadric_diffusion” was used to determine the overall diffusion model of OmpA. One key issue for achieving a reliable determination of the global diffusion model is the decision which residues to include or exclude from this determination because residues with significant internal motions will not be representative of the overall diffusion tensor. We applied three criteria to determine which residues to include in the determination of the global diffusion model: the residues had to be located in regions of ordered secondary structure (β-barrel region), they had to have NOE values greater than 0.6, and they had to have R₂ and R₁ values within a single standard deviation of the average of all residues in the β-barrel. Furthermore, the last two criteria had to be satisfied for data collected at all three magnetic fields. Using these very stringent criteria the following 57 residues were used as inputs in “quadric_diffusion”: 8, 9, 11–15, 38–44, 50–55, 79–85, 91–95, 97, 99–102, 125–129, 135–142, 163–169. We first examined the two axially symmetric diffusion models by simply comparing the best fit χ² values because both models have the same number (4) of free fit parameters. The best fit χ² value of the “prolate” model was lower than that of the “oblate” model (838 versus 880), and hence the prolate model was preferred over the oblate model. The significance of the choice between the isotropic (1 free fit parameter), axially symmetric, and asymmetric (6 free fit parameters) diffusion models was determined by F-statistics. The prolate versus spherical models yielded an F-statistic value of 3.80, and the asymmetric versus prolate models yielded an F-statistic value of 1.68. Since the tabulated critical values at the 5% significance level are F_0.05(3,53) = 2.78 and F_0.05(2,51) = 3.18, the prolate model was considered significantly better than the isotropic model, but the asymmetric model had no significant advantage over the prolate model. Therefore, we chose the prolate global diffusion model in all subsequent model-free calculations.

The best-fit prolate model yielded an overall isotropic rotational correlation time τ_c of 21.5 ns, and a diffusion coefficient ratio D_II/D_⊥ of 1.62. The two spherical angles (θ, ϕ) for orienting the major diffusion axis in the prolate model within the PDB frame were 92.1° and 90.1°, respectively. These initial diffusion model parameters were further optimized with the incorporation of all additional residues in the model-free formalism as described in Materials and Methods, and the final τ_c was determined to be 20.8 ns, and the final D_II/D_⊥ value was 5.75. This isotropic rotational correlation time agrees very well with the estimated protein/micelle mass of 45 kDa measured by dynamic light scattering[29]. The spherical angles (θ, ϕ) of (94.0°, 95.4°) indicate that the axis of rotational symmetry is essentially collinear with the normal of the β-barrel, i.e., perpendicular to the bilayer surface if the protein were inserted into a membrane. This orientation indicates that the OmpA molecule rotates around β-barrel axis much faster than around any perpendicular axis. The OmpA/detergent micelle complex likely has detergent molecules laterally associated around the hydrophobic perimeter of the barrel as determined by measuring solvent exchange (unpublished data), by MD simulation[30], or by intermolecular NOE and paramagnetic probe studies of another β-barrel membrane protein[31, 32]. Depending on the size of the radial extension of the lipid micelle, this would give it a more spherical or in extreme cases even an oblate physical shape. The high axial ratio of the diffusion coefficients with a fast rotation around the barrel axis indicates that the rotation of the protein is at least partially uncoupled from that of the protein/detergent complex. In fact, the interior of the lipid micelle might tolerate the independent rotation of the protein around the barrel axis since such rotation does not disrupt hydrophobic contacts between the lipid and the protein. By contrast, rotations perpendicular to the barrel axis are hindered within the micelle and the protein/detergent complex can rotate only as a single entity around any perpendicular axis.

Generalized Order Parameters

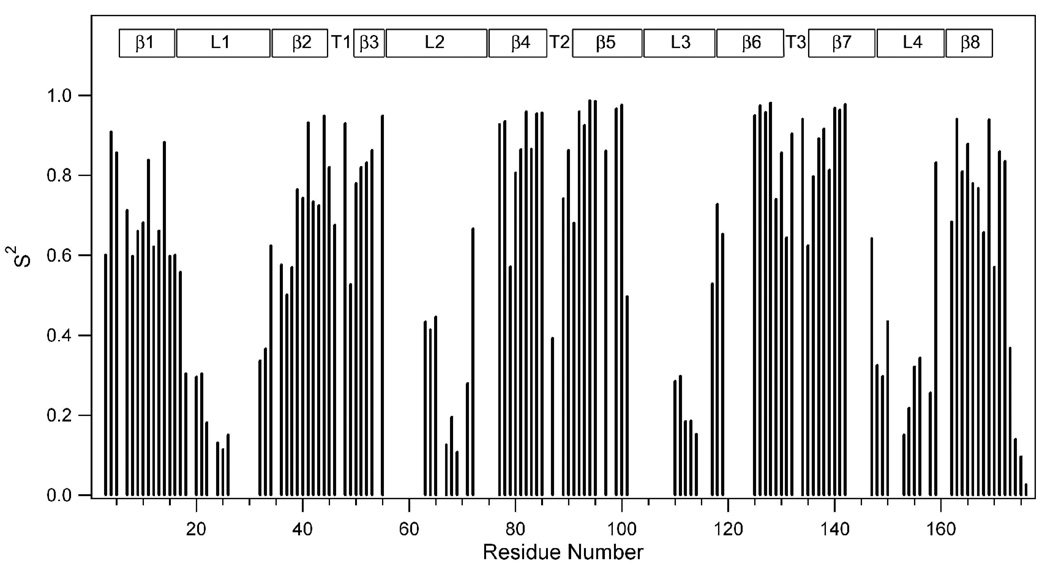
The nine data sets measured at three magnetic fields were globally analyzed by the extended model-free formalism excluding conformational exchange as described in Materials and Methods. The iterations determined for each residue which of five models explained in the Appendix fitted best its relaxation behavior. The results are summarized in Table 1. Figure 2 shows the derived squared generalized order parameters S² versus residue number of the OmpA TM domain. Back-calculated relaxation data from these best fits are included as red bars in Figure 1 and Supplemental Figures S1 and Supplemental Figures S2. With a very few exceptions the fits with the experimental data are excellent. S² is a measure of the amplitude of internal backbone motions on the ps-ns time scale. Order parameters can range from 0 to 1, where 1 indicates that the vector experiences no internal motions and 0 indicates that the vector is fully mobile and does not share any overall rotational motion with the protein as a whole. The data of Figure 2 indicate that S² varies dramatically along the sequence of OmpA and that its magnitude depends greatly on whether the residues are part of the β-structured region of the protein or not. The average S² value of all residues that participate in the β-barrel is 0.80, whereas the rest of the protein has an average S² of 0.43. When mapped onto the structure of OmpA, it is clear that the order parameters are largest in the center of the barrel (i.e., the plane corresponding to the mid-plane of the bilayer if the protein were inserted into a membrane) and that they decrease gradually the further away they are from this mid-plane (Figure 3A). This overall dynamic behavior of the protein anti-correlates with the dynamics of the lipid bilayer: the more rigid center of the β-barrel lines up with the most dynamic parts of the lipid tails in the center of the bilayer, whereas the more dynamic ends of the β-barrel contact the less dynamic headgroup regions of the lipids in a bilayer[33, 34]. The residues outside the limits of the lipid bilayer show dramatically increased degrees of mobility. The C-terminal and middle residues of the loops are the most dynamic regions of the protein. They reach order parameters as low as ~0.1. These differences in dynamics of different regions of OmpA were also seen in previous measurements of residual dipolar couplings (RDCs) and paramagnetic relaxation enhancements (PREs). In the RDC experiments, the loop and C-terminal residues exhibited very limited alignments even when the well ordered regions of the protein were adequately aligned[8]. In the PRE experiments, distances measured to these mobile residues showed “closest-contact” values indicative of their dynamic nature[9].

Table 1.

Internal motion parameters for OmpA as analyzed by the extended model-free formalism ^a

Residue	2°	Internal model	S2	Sf2	Ss2	τe (ps)	τf (ps)	τs (ns)
K3	N	{S2, $S_f^2$, τf,τs}	0.601	0.941	0.639		57.5	17.3
D4		{S2, τe}	0.909			775.1
N5		{S2, $S_f^2$τs}	0.856	0.920	0.930			3.8
T6	β1	N/M
W7		{S2, $S_f^2$τf, τs}	0.712	0.947	0.752		95.7	22.6
Y8		{S2, τe}	0.598			21325.0
T9		{S2, $S_f^2$τf, τs}	0.660	0.971	0.680		246.5	19.2
G10		{S2, $S_f^2$τf, τs}	0.681	0.900	0.757		29.2	6.5
A11		{S2, τe}	0.838			685.2
K12		{S2, $S_f^2$τf, τs}	0.622	0.987	0.630		62.6	34.3
L13		{S2, $S_f^2$τf, τs}	0.661	0.984	0.672		63.3	29.1
G14		{S2, τe}	0.883			1723.9
F15		{S2, $S_f^2$τf, τs}	0.598	0.977	0.612		368.7	25.6
S16		{S2, $S_f^2$τs}	0.601	0.837	0.718			1.8
Q17	L1	{S2, $S_f^2$τf, τs}	0.557	0.929	0.600		580.8	8.8
Y18		{S2, $S_f^2$τf, τs}	0.304	0.712	0.428		66.7	2.8
D20		{S2, $S_f^2$τf, τs}	0.295	0.822	0.359		495.8	7.2
T21		{S2, $S_f^2$τs}	0.304	0.825	0.369			1.3
G22		{S2, $S_f^2$τf, τs}	0.182	0.611	0.297		120.6	3.9
I24		{S2, $S_f^2$τs}	0.131	0.882	0.148			1.2
N25		{S2, $S_f^2$τs}	0.113	0.843	0.134			1.1
N26		{S2, $S_f^2$τf, τs}	0.151	0.662	0.229		79.6	2.1
E32		{S2, $S_f^2$τf, τs}	0.336	0.781	0.431		125.9	5.4
N33		{S2, $S_f^2$τf, τs}	0.366	0.741	0.495		60.3	5.5
Q34	β2	{S2, $S_f^2$τf, τs}	0.623	0.902	0.691		68.1	9.1
G36		{S2, $S_f^2$τf, τs}	0.577	0.965	0.598		115.8	25.6
A37		{S2, $S_f^2$τf, τs}	0.501	0.962	0.521		236.7	23.3
G38		{S2, τe}	0.570			20775.2
A39		{S2, $S_f^2$τf, τs}	0.764	0.970	0.788		281.6	11.5
F40		{S2, τe}	0.742			15597.0
G41		{S2, τe}	0.931			2722.1
G42		{S2, τe}	0.734			16825.6
Y43		{S2, τe}	0.724			20239.5
Q44		{S2, τe}	0.949			1235.2
V45		{S2, τe}	0.820			7718.2
N46	T1	{S2, τe}	0.675			386.5
Y48		{S2}	0.929
V49	β3	{S2, $S_f^2$τf, τs}	0.527	0.944	0.558		167.8	20.0
G50		{S2, $S_f^2$τf, τs}	0.781	0.982	0.795		64.7	28.0
F51		{S2, $S_f^2$τf, τs}	0.820	0.971	0.845		82.8	10.3
E52		{S2, $S_f^2$τf, τs}	0.831	0.981	0.848		143.3	21.1
M53		{S2, τe}	0.863			8755.5
G54		N/M
Y55		{S2, τe}	0.949			3771.5
Y63	L2	{S2, $S_f^2$τf, τs}	0.433	0.804	0.539		121.6	3.9
K64		{S2, $S_f^2$τf, τs}	0.413	0.797	0.519		232.2	6.3
G65		{S2, τe}	0.446			882.6
V67		{S2, $S_f^2$τf, τs}	0.126	0.547	0.230		99.8	2.9
E68		{S2, $S_f^2$τs}	0.195	0.816	0.240			1.1
N69		{S2, $S_f^2$τs}	0.107	0.732	0.147			1.1
A71		{S2, $S_f^2$τf, τs}	0.279	0.649	0.431		71.3	3.7
Y72		{S2, $S_f^2$τf, τs}	0.666	0.836	0.797		366.4	2.0
V77	β4	{S2, τe}	0.927			774.3
Q78		{S2, τe}	0.935			1044.1
L79		{S2, $S_f^2$τs}	0.572	0.992	0.576			23.5
T80		{S2, τe}	0.806			14921.2
A81		{S2, τe}	0.865			23784.9
K82		{S2, τe}	0.959			138.3
L83		{S2, τe}	0.865			1369.7
G84		{S2, τe}	0.954			180.6
Y85		{S2, τe}	0.956			871.1
I87	T2	{S2, $S_f^2$τf, τs}	0.392	0.911	0.430		325.6	25.0
D89		{S2,$S_f^2$ τs}	0.742	0.859	0.864			2.0
D90		{S2, $S_f^2$τs}	0.863	0.951	0.908			0.8
L91	β5	{S2, $S_f^2$τs}	0.681	0.869	0.783			5.3
D92		{S2, τe}	0.958			1515.8
I93		{S2, τe}	0.925			3146.7
Y94		{S2, τe}	0.986			738.3
T95		{S2, τe}	0.985			169.6
R96		N/M
L97		{S2, $S_f^2$τs}	0.861	0.941	0.914			2.0
G99		{S2, τe}	0.967			1441.3
M100		{S2, τe}	0.977			745.3
V101		{S2, τe}	0.497			24680.7
F102		N/M
R103		N/M
V110	L3	{S2, $S_f^2$τf, τs}	0.285	0.654	0.436		67.2	3.1
Y111		{S2, $S_f^2$τf, τs}	0.297	0.783	0.380		54.6	1.6
G112		{S2, $S_f^2$τf, τs}	0.185	0.609	0.303		77.2	2.7
K113		{S2, $S_f^2$τf, τs}	0.186	0.635	0.293		39.7	1.6
N114		{S2, $S_f^2$τf, τs}	0.153	0.577	0.264		67.7	2.1
T117		{S2, $S_f^2$τs}	0.528	0.865	0.611			0.9
G118	β6	{S2, τe}	0.727			2343.5
V119		{S2, $S_f^2$τf, τs}	0.653	0.823	0.794		60.3	3.6
G125		{S2, τe}	0.949			4126.3
G126		{S2, τe}	0.975			5644.8
V127		{S2, τe}	0.958			3531.9
E128		{S2, τe}	0.982			6837.4
Y129		{S2, $S_f^2$τs}	0.740	0.863	0.857			1.9
A130		{S2, $S_f^2$τf, τs}	0.856	0.950	0.901		268.7	10.1
I131	T3	{S2, $S_f^2$τf, τs}	0.644	0.929	0.693		222.3	19.9
T132		{S2, τe}	0.905			2654.8
E134		{S2, τe}	0.941			158.9
I135	β7	{S2, $S_f^2$τf, τs}	0.624	0.837	0.745		34.7	9.2
A136		{S2, $S_f^2$τf, τs}	0.797	0.976	0.817		127.1	16.2
T137		{S2, τe}	0.891			1158.1
R138		{S2, τe}	0.916			2899.4
L139		{S2, $S_f^2$τf, τs}	0.813	0.970	0.838		85.2	14.5
E140		{S2, τe}	0.967			2278.3
Y141		{S2, τe}	0.964			2109.0
Q142		{S2, τe}	0.978			3246.8
I147	L4	{S2, τe}	0.642			20.2
G148		{S2, $S_f^2$τs}	0.325	0.959	0.339			1.5
D149		{S2, $S_f^2$τf, τs}	0.297	0.807	0.368		92.5	1.5
A150		{S2, $S_f^2$τs}	0.435	0.857	0.507			1.2
I153		{S2, $S_f^2$τf, τs}	0.151	0.578	0.262		64.7	2.7
G154		{S2, $S_f^2$τf, τs}	0.217	0.636	0.341		147.4	3.7
T155		{S2, $S_f^2$τf, τs}	0.321	0.679	0.473		100.5	2.0
R156		{S2, $S_f^2$τf, τs}	0.343	0.645	0.532		130.1	4.0
D158		{S2, $S_f^2$τf, τs}	0.255	0.648	0.394		82.5	2.1
N159		{S2, τe}	0.832			84.8
L162		{S2, $S_f^2$τf, τs}	0.684	0.841	0.814		62.3	4.6
S163		{S2, τe}	0.941			2922.1
L164		{S2, $S_f^2$τf, τs}	0.810	0.973	0.833		134.4	15.0
G165	β8	{S2, $S_f^2$τs}	0.878	0.933	0.940			1.3
V166		{S2, τe}	0.780			22728.5
S167		{S2, $S_f^2$τf, τs}	0.767	0.962	0.798		178.7	14.8
Y168		{S2, $S_f^2$τf, τs}	0.657	0.979	0.671		245.2	21.6
R169		{S2, τe}	0.940			51.4
F170	C	{S2, $S_f^2$τf, τs}	0.570	0.964	0.592		97.2	16.0
G171		{S2, $S_f^2$τs}	0.859	0.924	0.930			1.1
Q172		{S2, $S_f^2$τf, τs}	0.835	0.919	0.909		177.4	7.0
G173		{S2, $S_f^2$τf, τs}	0.368	0.735	0.501		44.2	1.2
E174		{S2, $S_f^2$τf, τs}	0.140	0.537	0.260		72.8	1.9
A175		{S2, $S_f^2$τf, τs}	0.096	0.448	0.215		56.2	0.7
A176		{S2, $S_f^2$τf, τs}	0.026	0.175	0.151		61.2	0.5

^aThe analysis was performed using the program Relax[21, 22] without the parameter R_ex. N/M, no model.

Figure 2.

Squared generalized order parameters of the backbone amide N-H vector of the OmpA TM domain in DPC micelles at 50 °C. Regions of secondary structures are indicated on the top as in Fig. 1.

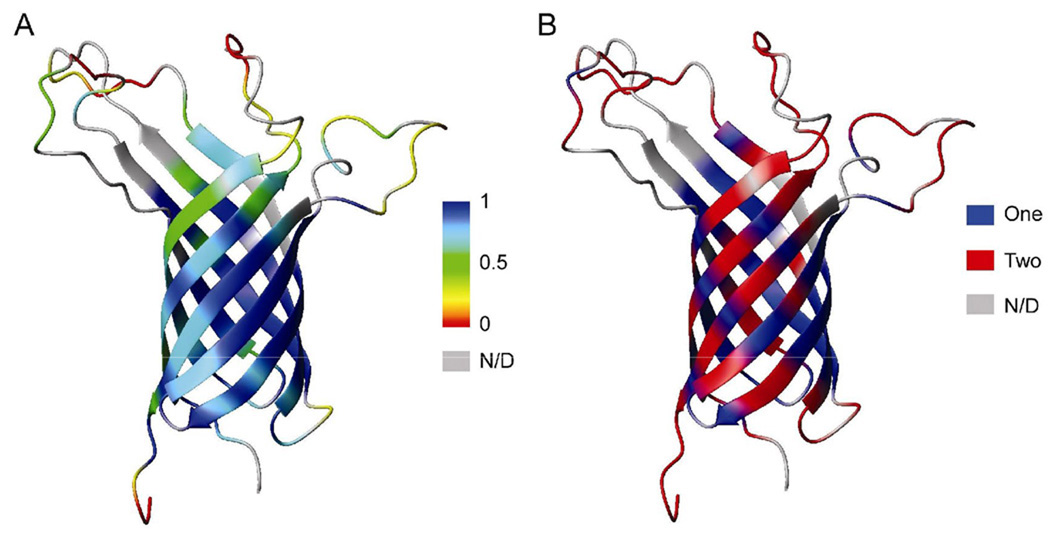
Figure 3.

Squared generalized order parameters (A) and the number of time scales used to describe internal motions (B) mapped onto ribbon representations of the structure of the OmpA TM domain (PDB code 2GE4).

Internal Motions

The extended model-free formalism offers an opportunity to reveal internal motions on two distinct time scales. More than half of all residues of OmpA are best-fit with motions on two time scales (Table 1). Internal motions on the fast time scale (tens of ps) usually reflect fast random thermal motions. On the other hand, slow internal (but still significantly faster than τ_c) motions are usually observed for residues of certain regions of the protein that undergo concerted motions, and therefore, are likely more relevant for protein function. The residues that exhibit internal motions on two time scales are marked red in the ribbon diagram of OmpA shown in Figure 3B, whereas residues whose dynamics are sufficiently described by a single internal motion are indicated in blue. Most residues in the extracellular loops are best fit with internal motions on two time scales, indicating that the loop residues are undergoing relatively slow concerted motions that are coupled with faster thermal motions. Most loop residues move on a time scale of 1–5 ns and sometimes slower near their anchoring points in the β-barrel. They become increasing more disordered (lower S_s²) the further away the residues are from their anchoring points (Figure 2). This motional behavior is perhaps best visualized as tentacles of a sea anemone moving with increasing speed and amplitude the further away they are from the stem of the animal. In contrast to the loop residues, the residues that form the β-barrel do not indicate a clear pattern in terms of their motional behaviors. Even residues that are best fit with internal motions on two time scales display slower motions with much lower amplitudes (higher S_s²) than their loop residue counterparts. Interestingly, many residues that display internal motions only on a single time-scale move on the ns rather than the ps time-scale. No clear correlations are evident between residues that have been found previously to participate in ion channel gating with their motional behaviors on the ps to ns times-scale. This is perhaps not surprising because gating of OmpA happens on ms or longer time-scales[11].

Possible Conformational Exchange Processes

Five residues in Table 1 could not be fit with any model. They include Thr6, Gly54, Arg96, Phe102, and Arg103. These residues actually had no internal motions, i.e., S²=1, in the final outputs of the calculations. When we inspected the final back-calculated values for these residues, they showed quite poor fits. In other words, even the most complex of our models did not yield statistically better fits than the rigid-rotor model. Since T_1ρ and CPMG dispersion experiments can only detect conformational exchange processes between ~50 µs and ~10 ms, it is possible that some residues might undergo conformational exchange on time scales outside this window and hence may not have been detected by our relaxation dispersion experiments. Therefore, we performed a second round of model-free analysis, in which R_ex terms were permitted and included when yielding better fits (see Appendix, for models). The results of the best fits using this set of fitting models are shown in Supplementary Table S1 and the generalized order parameters derived from these fits are displayed in Supplemental Figure S3A. Indeed, when R_ex was included in the model-free analysis, Thr6, Arg96, and Arg103 were best fit with model {R_ex}, Phe102 was best fit with model {S₂, R_ex}, whereas Gly54 was still best fit with model {}. All charged residues that face the lumen of the barrel and that might be involved in ion conduction through the OmpA channel[5, 10, 11], i.e. Lys12, Glu52, Lys82, Arg96, Glu128, Arg138, and Glu140 indicated various degrees of R_ex contribution according to this analysis (Supplemental Table S1). Therefore, it is possible that these residues undergo conformational exchange on the ms-µs time-scale, but outside the 0.05–10 ms window, and that these motions could be important for the activity of the OmpA ion channel. However, many other residues (77 of 125 analyzed) also have R_ex terms when R_ex is permitted in this set of model-free analysis. In fact, as shown in Supplemental Figure S3B, the residues showing R_ex are almost randomly distributed over all regions of the protein so that we are cautious with attributing special significance to them.

Discussion

The backbone dynamics of the β-barrel integral membrane protein OmpA have been measured at three magnetic fields and have been analyzed in the framework of the extended model-free formalism. Even when R_ex terms are included in the calculations, the system is well determined with nine independent measurements for a maximum of five internal motion parameters per residue. When R_ex terms are excluded, the system is even better determined because only up to four internal motion parameters (S²,$S_f^2$, τ_f, and τ_s ) need to be considered to describe the internal motions of each residue. This latter method is our preferred method of analysis because we have been unable to find direct evidence for ms-µs exchange motions by relaxation dispersion experiments. The back-calculated relaxation data generally match the experimental data very well (Figure 1, Supplemental Figures S1 and S2), adding confidence that our methods correctly describe the internal and global motions, even if the resulting picture of the dynamics of OmpA in DPC micelles turned out to be quite complicated.

OmpA has been found to rotate globally with axial symmetry around the barrel axis. This rotation around the protein’s long axis is more than five times faster than around perpendicular axes, indicating that OmpA most likely rotates along this axis within the micelle, but as an entity together with the micelle around perpendicular axes. Furthermore, the internal motions near the center of the β-barrel are quite limited (high S²), but increase towards the barrel ends, which are likely contacting the polar headgroups of the surrounding DPC molecules in the micelle. Once the loops emerge beyond the headgroup region into water they become particularly flexible and move with progressively larger amplitudes like the tentacles in a sea anemone.

Despite these general trends describing the dynamical properties of OmpA, no clear correlations appear to exist between the complexity of motions, i.e. whether one or two time-scales of internal motions best describe the data, and the relative properties and positions of the residues in the protein. Hydrophobic and hydrophilic, lipid-exposed and internal, potentially ion conducting and non-conducting residues experience a diversity of motions irrespective of their structural and functional roles. Despite the lack of such structural and functional correlations, we find that the generally more flexible residues tend to be better modeled with internal motions on two time-scales than on a single time-scale.

Hwang et al. were able to measure conformational exchange of several residues of the β-barrel membrane protein PagP in CYFOS-7 micelles by ¹⁵N-CPMG relaxation dispersion experiments and found a global exchange rate of 331 ± 41 s⁻¹ for their protein[35]. We do not know why PagP and OmpA behaved differently in this regard although the same experimental protocols and similar measuring temperatures were applied in our current attempts to measure such conformational exchange with OmpA. PagP is an enzyme that was shown to exist in two conformational states involving whole regions of the protein. OmpA on the other hand is a structural and ion channel protein that may not undergo such global backbone conformational changes, but rather more localized side-chain conformational exchanges that may only be detectable by measuring side-chain conformational dynamics, which was not attempted here.

Global Diffusion and Internal Motion Models

As explained in the Appendix, the global diffusion model and internal model-free models jointly define the spectral density function. We have used the routine “full_analysis.py” in the program “Relax” to analyze our OmpA relaxation data in an attempt to optimize internal and global parameters simultaneously. However, this approach did not converge, most likely because of the highly flexible nature of some portions of OmpA and its complex internal motion behavior that eventually emerged from the current analysis. To cope with this problem, we adopted the alternative iterative approach as described in Materials and Methods. Convergence of this iterative approach was good and resulted in well defined solutions of best model and parameter fits. Therefore, we believe that this approach may be useful to also analyze other proteins that have similarly complex internal motions with the extended model-free formalism. An earlier model-free analysis reported a two-domain approach to separate a more dynamic from a more rigid domain of a protein[36]. We did not attempt this approach here because OmpA cannot be easily subdivided into two domains with distinct motional properties. For our approach to work, it is important to choose very conservatively the residues that are selected to determine the initial estimate of the global diffusion tensor. Only the most rigid residues, but distributed over the whole main body of the protein must be selected initially for this purpose. Once this is done properly, the more flexible residues can be added back in order to determine the final diffusion tensor. This procedure minimizes the likelihood of finding a false minimum in the process of defining the diffusion tensor.

Possible Limitations of the Model-Free Formalism for Membrane Proteins

The selection of internal motion models for the different residues of OmpA was based solely on statistical criteria. Nevertheless, the best model only reflects the fact that the selected model is in each case statistically the best among all candidate models. It still does not mean that the best model describes the absolutely “correct” motions of the residues in our protein. Motions of membrane proteins may be different from those of soluble proteins, for which the formalism was originally derived. Because of the complexity of their detergent micelle environment, membrane proteins such as OmpA may experience anisotropic internal motions that are different from those of globular proteins in aqueous solution. For example, internal protein motions may be different in the apolar hydrocarbon, polar headgroup, and water environments of the lipid micelle. In the case of OmpA, the central β-barrel residues are in contact with the acyl chains of the lipid, whereas loop residues and N- and C-termini are exposed to water. The aromatic residue-rich ends of the barrel are mostly in contact the polar headgroups of the lipid. Not only is the chemical environment different in these different regions of the protein, but the lipids themselves experience dynamic gradients from the lipid-water interface into the hydrophobic core. Although such complex anisotropic solvent motions would be interesting, but very difficult to implement in a detailed motion analysis of the embedded membrane protein, the generalized order parameters derived from the present analysis should still be mostly valid. The products of the generalized order parameters generally describe total internal motions pretty well, regardless of whether they can be subdivided into different nested motions or not, as has been confirmed when the original model-free formalism was expanded to the extended formalism with internal motions on two time-scales[15].

Appendix

Model-free models and fitting parameter sets

The model-free formalism separates overall (global) and internal (residue-specific) motions. There are four different global diffusion models and the number of parameters describing these models vary from 1 to 6[12]:

1. spherical: D_iso;

2. axially symmetric (prolate): D_II, D_⊥, θ, ϕ with D_II > D_⊥;

3. axially symmetric (oblate): D_II, D_⊥, θ, ϕ with D_II < D_⊥; and

4. asymmetric: D_x, D_y, D_z, α, β, γ,

where D_iso, D_II, D_⊥, D_x, D_y, D_z terms are the principal components of diffusion tensor in the respective models. In the case of axially symmetric diffusion, D_II is the axis of rotational symmetry and θ and ϕ are spherical angles orienting the unique axis of the diffusion tensor within the PDB coordinate frame of the protein structure. α, β, and γ are Euler angles relating the diffusion tensor coordinates to the structural coordinates in the asymmetric model.

For proteins experiencing isotropic/spherical diffusion, the original model-free formalism[13, 14] defines the spectral density function as:

$$J(\omega )=\frac{2}{5}\left[\frac{S^2{\tau }_c}{1+{(\omega {\tau }_c)}^2}+\frac{(1-S^2){\tau }_e^{\text{'}}}{1+{(\omega {\tau }_e^{\text{'}})}^2}\right]$$ (1)

where the overall rotational correlation time τ_c equals (6D_iso)⁻¹. S is the generalized order parameter that can vary from 0 to 1. τ_e’ = (1/τ_c + 1/τ_e)⁻¹ and τ_e is the internal correlation time. The extended model-free formalism[15] takes into account internal motions on two different time scales, fast and slow:

$$J(\omega )=\frac{2}{5}\left[\frac{S^2{\tau }_c}{1+{(\omega {\tau }_c)}^2}+\frac{(1-S_f^2){\tau }_f^{\text{'}}}{1+{(\omega {\tau }_f^{\text{'}})}^2}+\frac{(S_f^2-S^2){\tau }_s^{\text{'}}}{1+{(\omega {\tau }_s^{\text{'}})}^2}\right]$$ (2)

where S_f and S_s are order parameters of internal motions on fast and slow time scales, respectively, and $S^2=S_f^2{S}_s^2$. τ_s,f’ = (1/τ_c + 1/τ_s,f)⁻¹ and τ_s and τ_f are internal correlation times on slow and fast time scales, respectively. Both the original and extended model-free models can be simplified if τ_e and τ_f are sufficiently small, i.e., if they contribute negligibly to the spectral density function:

$$J(\omega )=\frac{2}{5}\frac{S^2{\tau }_c}{(1+{\omega }^2{\tau }_c^2)}$$ (3)

$$J(\omega )=\frac{2}{5}\left[\frac{S^2{\tau }_c}{1+{(\omega {\tau }_c)}^2}+\frac{(S_f^2-S^2){\tau }_s^{\text{'}}}{1+{(\omega {\tau }_s^{\text{'}})}^2}\right]$$ (4)

Function (3) can be further simplified for rigid rotors where S²=1:

$$J(\omega )=\frac{2}{5}\frac{{\tau }_c}{(1+{\omega }^2{\tau }_c^2)}$$ (5)

In conclusion, there are five different internal model-free models of increasing complexity with the following parameter listings:

• {}

• {S²}

• {S², τ_e}

• {S²,$S_f^2$, τ_s}

• {S²,$S_f^2$, τ_f, τ_s}

These models correspond to functions of (5), (3), (1), (4), and (2) respectively.

If the residues additionally experience conformational exchange on the ms-µs time scale, this process will contribute to the transverse relaxation rate R₂. Therefore, if the field-dependent R_ex term is added to each of aforementioned model-free models they have the following parameter listings:

• {R_ex}

• {S², R_ex}

• {S², τ_e, R_ex}

• {S², $S_f^2$, τ_s, R_ex}

• {S²,$S_f^2$, τ_f, τ_s, R_ex}

In summary, ten different model-free models have been deduced from combinations of up to five parameters to describe the internal motions of proteins. Functions (1) through (5) are described here only for molecules experiencing isotropic diffusion with only τ_c as the single global parameter describing the overall rotation. For the axially symmetric and asymmetric diffusion cases, the global correlation times in functions (1) though (5) have to be fractionalized with angle-dependent diffusion tensor terms. In these, but not in the isotropic diffusion case input of the protein structure is required.