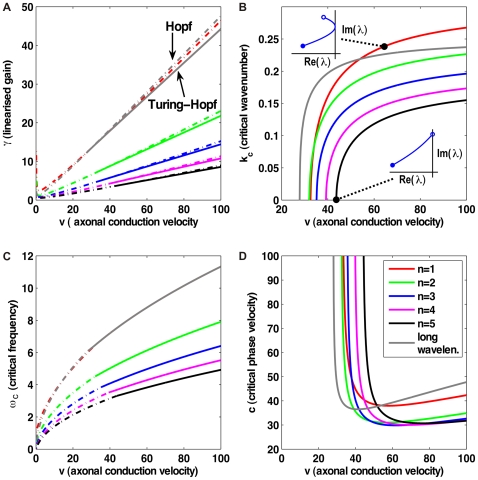
Figure 9. Turing instability analysis of the dispersive and long-wavelength propagators.
Bifurcations are investigated by varying the axonal conduction velocity 
and determining 
, 
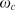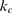, and the critical linearized gain 
. All other model parameters remain at the values discussed in the text. (A) Solid curves represent Turing-Hopf bifurcations (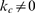
), dot-dashed curves Hopf bifurcations (
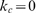). Results for orders 
of the dispersive propagator and for the long-wavelength model are shown. Above the Turing-Hopf curves travelling waves emerge, whereas above the Hopf curves bulk oscillations are seen. Stability will be lost at a given 
through the less stable bifurcation, which has smaller critical 
. (B) Critical wavenumber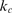 
of the Turing-Hopf bifurcation. Insets show the position in the complex plane of the most weakly damped pole under variations of 
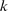(open circles 
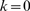, closed circles 
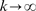) for the dispersive model at the indicated 
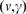. (C) Critical frequency 
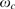of the less stable bifurcation. (D) Critical phase velocity 
, shown where Turing-Hopf is the less stable bifurcation.