Table 6. Comparison of linear Turing instability analysis with numerical integrations for the dispersive propagator.

		&
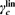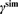
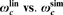
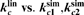
1	50	22.33	8.04	0.21	linearization
		23	8.38	0.14, 0.22	simulation
	100	44.27	11.34	0.27	linearization
		45	11.73	0.22, 0.28	simulation
3	50	7.23	4.54	0.15	linearization
		8	4.82	0.09, 0.17
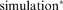
	100	14.43	6.41	0.20	linearization
		14.5	6.92	0.18, 0.26

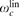For selected orders and conduction velocities linear Turing instability analyses of Eqns. (66)–(68) were used to predict the critical Turing-Hopf , , and 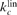, cf. Fig. 9. For numerical simulations, a 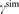somewhat larger than 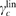was chosen. The space-averaged 1D temporal Fourier spectrum 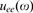was used to estimate 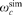as the maximum of 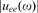. The time-averaged 2D spatial Fourier transform 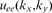was used to obtain two estimates: 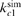as the 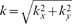for which 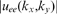is maximal; and 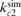as the 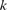for which the mean of 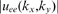over a circle around the origin with radius 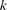is maximal. For the estimates grid time series of 50 time units with 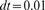(500 samples total) were recorded, after initial “transients” of 100 (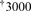) time units were discarded. The spatial grid was 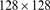(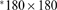) with discretization steps .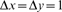