Abstract
Valdes-Sosa et al. (2000) introduced a transparent-motion design that provides evidence of surface-based processing of visual motion. We show that this design suffers from a motion-duration confound that admits an alternative explanation based on neuronal adaptation and competition. We tested this explanation by reversing the relationship between motion duration and which perceptual surface was “cued”. We also examined the role of color duration. Our findings support the surface-based account and, more specifically, demonstrate that this type of surface-based selection involves selective spatial processing at the scale of the texture elements that define the transparent surfaces.
Keywords: object-based attention, surface-based attention, transparent motion, biased competition, area MT
1. Introduction
Visual processing is selective -- few stimuli that impinge the retinae reach perceptual awareness and/or elicit behavioral responses. Selective processing based on location (e.g. Posner 1980; Posner & Cohen, 1984; Treisman & Gelade, 1980) or individual features (e.g. Aine & Harter, 1986; Anllo-Vento & Hillyard, 1996) is well-established and easy to reconcile with the organization of the visual cortex into retinotopic maps and feature columns. There is growing evidence, however, that whole objects or surfaces can be selectively processed (e.g. Duncan 1984; O’Craven, Downing, & Kanwisher, 1999; Blaser, Pylyshyn, & Holcombe, 2000; Valdes-Sosa, Cobo, & Pinilla, 2000). The mechanisms underlying such object- or surface-based selection are unclear. We have argued (e.g. Mitchell, Stoner, Fallah, & Reynolds, 2003; Reynolds, Alborzian, & Stoner, 2003; Mitchell, Stoner, & Reynolds, 2004) that the transparent-motion design offered by Valdes-Sosa et al. (2000) has provided the best evidence of object- or surface-based selection (we mostly use the later phrase hereafter) to date, but in this study we tested an alternative (i.e. non-surface-based) account of that design. Our findings are consistent with surface-based selection and shed light on the underlying mechanisms.
1.1. Transparent motion and surface-based attention
The transparent-motion design introduced by Valdes-Sosa et al. has been adapted to study various aspects of surface-based selection including perceptual mechanisms (Lopez, Rodriguez, & Valdes-Sosa, 2004; Mitchell et al. 2003; Reynolds et al. 2003; Rodriguez, Valdes-Sosa, & Freiwald, 2002), single-unit correlates in the non-human primate (Fallal, Stoner, & Reynolds, 2007), event-related potentials (ERPs) in humans (Khoe, Mitchell, Reynolds, & Hillyard, 2005; Pinilla, Cobo, Torres, & Valdes-Sosa, 2001; Valdes-Sosa, Bobes, Rodriguez, & Pinilla, 1998), and interactions between selective attention and binocular rivalry (Mitchell et al. 2004). While stimulus and behavioral details in the above studies varied somewhat, in all of those studies (except for Fallah et al. in which there was no behavioral component) subjects were asked to judge brief translations of one of two superimposed dot fields, which (excepting the brief translations) rotated in opposite directions (i.e. clockwise and counterclockwise). It has been found that translations of dot fields that are “cued” (endogenously or exogenously) are judged accurately relative to translations of the other (“uncued”) dot field. This design is meant to rule out both spatial and feature-based selection as an explanation for the performance bias. Spatial selection (at least at a coarse scale) is ruled out by spatial superimposition of the two dot fields. Motion-based selection is ruled out since the direction of the translation is unpredictable. By removing the color differences between the two dot fields, Mitchell et al. (2003) have also demonstrated that the performance bias is not color-based. Instead, these results have been taken as evidence of surface-based selection whereby the successive motions (i.e. the rotation followed by the translation) of a cued perceptual surface are preferentially processed relative to motions of an uncued surface.
1.2. The motion-duration confound
In considering how preferential processing of a cued dot field’s rotation direction might give rise to preferential processing of that dot field’s translation direction, we realized that previous designs suffered from a motion-duration confound that admitted an explanation not requiring surface-based selection. This confound applies to both the original “two-translation” design devised by Valdes-Sosa et al. (2000) and to the “delayed-onset” design introduced by Reynolds et al. (2003) in which there is only a single translation. This confound provides a challenge to the interpretation of the numerous studies that have used these designs (cited above). We first illustrate this confound with the delayed-onset design, since it is more obvious in that design and because we use the delayed-onset design in this study.
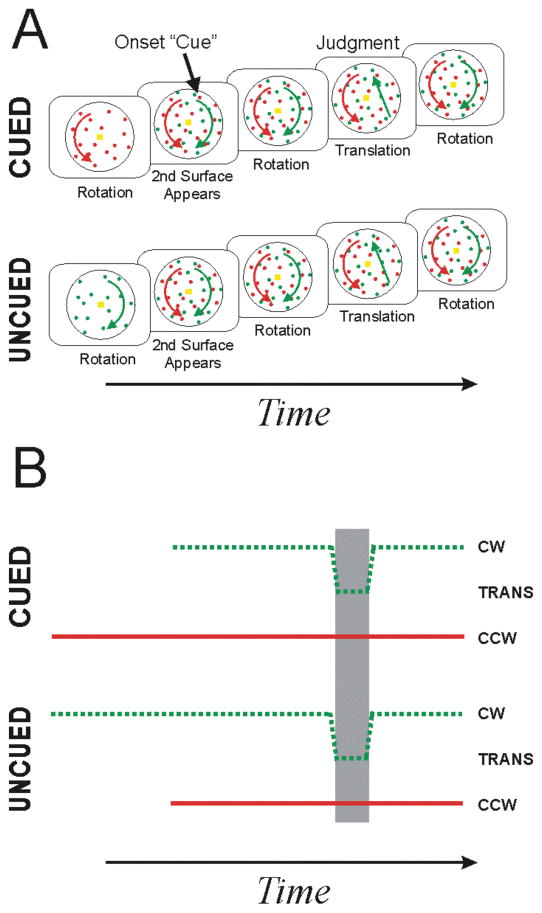
Figure 1 shows two complementary depictions of the delayed-onset design. Figure 1A illustrates the appearance of the transparent-motion stimuli as two counter-rotating perceptual surfaces. The depiction in Figure 1B, conversely, explicitly shows the relative duration of each type of motion, thereby more clearly revealing the motion-duration confound. In this later depiction, the dots of the two dot fields are distinguished by line style (dashed or solid), dot color is given by line color, and type of motion (i.e. clockwise, counterclockwise, or translation) is given by vertical line placement. The difference in the onset times of the two dot fields yields the motion-duration confound (gray region): translations of the “cued” (i.e. delayed) dot field occur in the presence of the older rotation direction, whereas translations of the “uncued” (i.e. non-delayed) dot field occur in the presence of the newer rotation direction.
Figure 1. Delayed-onset design.
A) Conventional depiction. Two superimposed dot fields rotate in opposite directions (about a central fixation target) yielding a perception of two transparent surfaces. One rotating dot field appears first followed by the “delayed” dot field. Subsequently, either the delayed (i.e. “cued”) or non-delayed (i.e. “uncued”) dot field translates briefly. After translation, both dot fields rotate. Subjects report the direction of the translation. Translations of the cued dot field are judged more accurately than translations of the uncued dot field. B) Feature-based depiction. Dot fields are distinguished by line style (dashed or solid), dot field color is given by line color, and type of motion (i.e. clockwise, counterclockwise, or translation) is given by vertical line placement. The onset differences in this design result in “cued” translations occurring in the presence of the older rotation direction and “uncued” translations occurring in the presence of the newer rotation direction (gray region).
The original design of Valdes-Sosa et al. (2000) had two successive translations (Figure 2A) and, as described below, it also suffers from a motion-duration confound. In this design, fixation target color (red or green) cues subjects as to which dot field translates first but the second translation can be of either dot field. With this design, it was found that subjects reported the first translation accurately, but the second translation was only judged accurately if it was of the same dot field that had earlier translated. The performance bias seen in judgments of the second translation was taken as evidence that endogenously-directed attention is surface-based and cannot rapidly switch between surfaces.
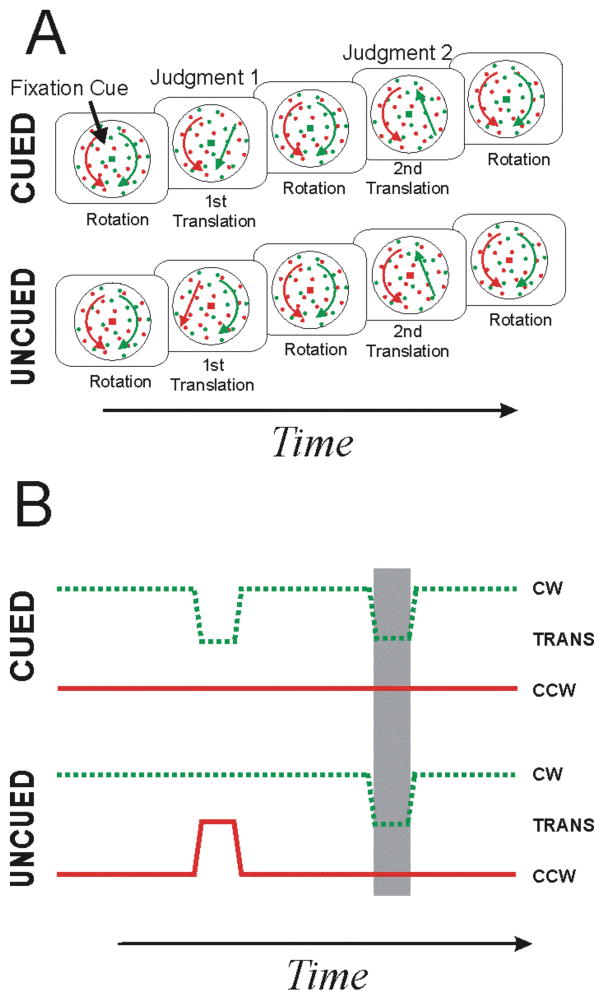
Figure 2. Two-translation task of Valdes-Sosa et al. (2000).
A) Conventional depiction. Fixation-point color (green as in upper panels or red as in lower panels) indicates which surface translates first. Following a period of rotation, the cued dot field translates briefly, while the other field continues to rotate. The dot fields then continue to rotate for a variable delay, at which point one dot field, chosen randomly, translates briefly. After this second translation, both surfaces rotate. Observers report the direction of each translation. It was found that the first translation is judged accurately, but the second translation is only judged accurately if it is of the same dot field that translated first. B) Feature-based depiction. Conventions are same as in Fig 1B. The first translation has been proposed to exogenously cue attention to the translating dot field (Reynolds et al. 2003). This first translation also leads to a motion-duration confound (gray region): cued second translations occur in the presence of the older (i.e. non-interrupted) rotation and uncued second translations occur in the presence of the newer (i.e. interrupted) rotation.
Reynolds et al. (2003) found that the performance bias reported by Valdes-Sosa et al. (2000) survived removal of the endogenous cue and hypothesized that the first translation exogenously attracted attention to the translating dot field. To test this interpretation, Reynolds et al. took advantage of the observation that abrupt onsets automatically capture attention (Yantis & Jonides, 1984; 1990). They replaced the first translation of the two-translation design with a delayed onset, reasoning that attention should be drawn to the delayed dot field. This created the delayed-onset design discussed above (Figure 1). The results with this design appeared to support Reynolds et al.’s interpretation in that translations of the delayed dot field were judged more accurately than translations of the non-delayed onset. Reynolds et al. concluded that the delayed onset, like the first translation in the two-translation design, exogenously attracted attention to the delayed dot field.
Reynolds et al.’s interpretation is challenged by the observation that the first translation of the two-translation design, like the delayed onset of the delayed-onset design, yields a motion-duration asymmetry between cued and uncued translations. As seen in Figure 2B, this asymmetry results because the first translation of one dot field interrupts one direction of rotation: a second translation of the same dot field (a “cued” translation) occurs in the presence of the older (i.e. non-interrupted) rotation, whereas a translation of the other dot field (an “uncued” translation) occur in the presence of the newer (i.e. interrupted) rotation (gray region). This motion duration asymmetry in turn admits a mechanistic explanation that does not invoke surface-based selection.
1.3. The motion-competition explanation
This study originated in our attempt to account for the neurophysiological and performance biases found with the Valdes-Sosa et al. design within the biased-competition account of stimulus selection (Desimone & Duncan, 1995). According to this account, when multiple stimuli appear in the visual field they activate distinct populations of neurons that compete with each other. Which neurons win this competition can be biased by the strength of the stimuli (such as dictated by luminance contrast) as well as by endogenously-directed selective attention (Luck, Chelazzi, Hillyard, & Desi-mone, 1997; Moran & Desimone 1985; and Reynolds, Chelazzi, & Desimone, 1999).
Studies of event-related potentials (ERPs) have reported that potentials associated with the middle temporal complex (MT+) are larger in responses to cued versus uncued translations in the Valdes-Sosa et al. design (Valdes-Sosa et al. 1998; Rodriguez & Valdes-Sosa, 2006; Valdes-Sosa, Bobes, Rodriguez, & Pinilla, 2004; Khoe et al, 2005). MT+ is known to be involved in visual motion processing in the human (Tootell, Reppas, Kwong, Malach, & Born, 1995; Wat-son, Myers, Frackowiak, Hajnal, & Woods, 1993) and is the probable human homolog of the middle temporal (MT) and medial superior temporal (MST) areas in the macaque.
Stimulus interactions consistent with competition between moving stimuli have been documented in both MT and MST. In particular, it has been found that superimposing a dot pattern moving in a neuron’s anti-preferred direction upon a dot pattern moving in that neuron’s preferred direction (thereby creating transparent motion) suppresses neuronal responses in area MT (Qian & Andersen, 1994; Snowden, Treue, Erickson, & Andersen, 1991). Similar evidence of suppressive or competitive interactions have been found with spatially separated stimuli in areas MT and MST (Recanzone & Wurtz, 2000; Recanzone, Wurtz, & Schwarz, 1997). Critically, for area MT, Krekelberg and Albright (2005) have found that responses to multiple stimulus components are modeled well by competitive interactions and that those interactions are not restricted to opposite directions. In particular, they found that a simple model of neuronal responses advanced to account for competitive stimulus interactions in cortical areas V2 and V4 (Reynolds et al. 1999) also nicely accounts for stimulus interactions within area MT.
We realized that the motion-duration asymmetry discussed above should, due to short-term neuronal adaptation, yield differences in the strengths of the neuronal responses to the two rotations in the Valdes-Sosa et al. design. Short-term neuronal adaptation refers to a decrease in neuronal response after stimulus onset and is found in the responses of the motion-selective neurons in areas MT (e.g. Priebe, Lisberger, & Churchland, 2002; Priebe & Lisberger, 2002) and MST (e.g. Duffy & Wurtz, 1997). Coupled with competitive motion interactions, adaptation might in turn account for the previously observed biases in ERP magnitude and psychophysical performance found with that design (see above).
To appreciate how adaptation and competition might account for these previous results, note that during translations in the delayed-onset design, neurons responding to the surviving rotation are responding to the older rotation for cued translations and to the newer rotation for uncued translations (gray region in Figure 1B). In consequence, neurons responding to the surviving rotation during cued translations should be more adapted than neurons responding to the rotation during uncued translations. If neurons responding to the rotation suppress neurons responding to the translation, then neurons responding to cued translations should be suppressed less than neurons responding to uncued translation. For brevity’s sake we refer to this as the “motion-competition” account, though both adaptation and competition are critical to this account. This framework also applies to responses of the second translation of the two-translation design (gray region in Figure 2B) since that design also suffers from a motion-duration asymmetry.
To make this account concrete, we have applied the above-mentioned motion competition model to detection of translations in cued and uncued trials (See Appendix for details). In this model, neurons receive excitatory and inhibitory (divisive) inputs. Figure 3A and B show the modeled responses to the two rotations under cued and uncued conditions, respectively. These adapting responses provide the inhibitory input to a translation-selective model neuron. In particular, the inhibition provided to the translation detector is simply the sum of the two responses to the two rotations. The time courses of inhibition for cued and uncued conditions are shown in Figures 3C and D, respectively. The critical time period is that during the translation as indicated by the light-gray vertical stripes. As seen in these figures, inhibition is greater during the translation for uncued than for cued conditions, reflecting the fact that the translation is competing primarily against the newer rotation (responses to the other rotation die out relatively quickly) for uncued conditions. In contrast, the excitatory input to the translation detector (indicated by arrows in Figures 3C and D) is the same for cued and uncued conditions.
Figure 3. Motion-competition explanation.
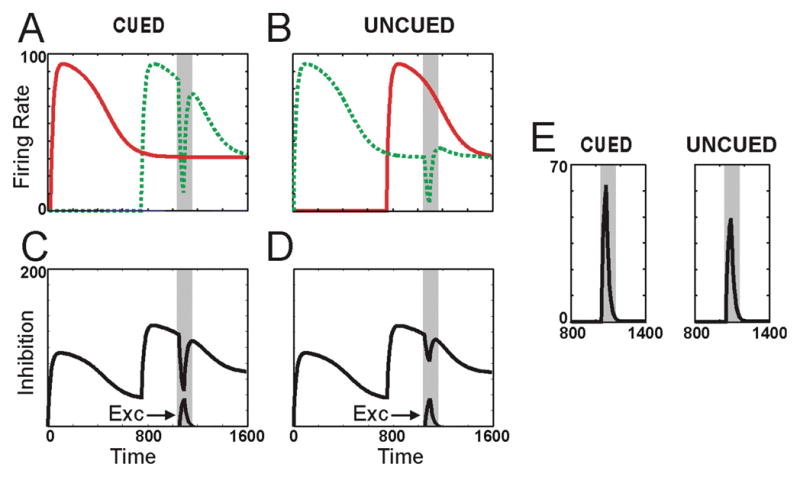
A) Adapting responses to CW (green) and CCW (red) rotating dots for cued conditions. B) Adapting responses to CW (green) and CCW (red) rotating dots for uncued conditions. C) Inhibition and excitation to translation detector for cued conditions. Inhibition is sum of responses to CW and CCW rotations (i.e. red and green traces in A). Excitation arising from the translation is indicated by arrow (“Exc”) and is scaled by 1/4 to avoid overlap with inhibitory traces. D) Same as C but for uncued conditions. Inhibition is greater than for cued conditions whereas excitation is the same. E) Response of translation detector is greater for cued (left) than for uncued (right) conditions due to the greater inhibition accompanying uncued conditions. Time is in msec.
Figure 3E shows the responses of the translation detector for cued and uncued conditions: responses to cued translations are ~21% larger than to uncued translations. This model provides a qualitative account for findings reporting larger ERPs to cued than uncued translations in the Valdes-Sosa et al. design. To account for the perceptual results, we assume that larger neuronal responses generally lead to better motion discrimination than do smaller responses. The motion-competition explanation thus assumes that the first translation of the two-translation design and the delayed onset of the delayed-onset design yield a performance bias, not because they act as exogenous attentional cues as proposed by Reynolds et al. (2003), but because they lead to differential adaptation of motion-selective neurons that suppress one another.
1.4. Testing the motion-competition model
To test the motion-competition model, we devised variations of the delayed-onset design that de-coupled motion duration from the exogenous cueing proposed to be elicited by delayed onset. Specifically, on some trials in Experiment 1 we introduced swaps in rotation-direction of the two dot fields. These swaps reversed the original relationship between motion duration and which dot field was cued by delayed onset. As we report after detailing our stimulus conditions in Methods, our motion-competition model predicts that these motion-duration switches should result in neuronal responses to translations of the delayed dot field being smaller than responses to translations of the non-delayed dot field. Assuming further that the psychophysical ability to discriminate translation direction is better for larger than for smaller neuronal responses, these reversals predict a corresponding reversal in psychophysical performance. In Experiment 2, we introduced color swaps in addition to the motion swaps. As outlined in the Discussion, performance shifts are also predicted to accompany color swaps if we assume color-selective adaptation or that selective processing of a cued dot field is based on color.
2. Methods
2. 1. Observers
Eleven subjects completed a full number of sessions for Experiment 1. Nine subjects completed a full number of sessions for Experiment 2, two of whom also participated in Experiment 1. These subjects achieved criterion performance by their fourth session: data from a subject’s first four sessions had to contain at least two conditions above chance performance (see below for statistical methods). Data from subjects that failed to reach criterion performance or could not complete a full number of experimental sessions were not included in the analyses presented here. With the exception of two observers in each experiment, the subjects in Experiments 1 and 2 were naïve with regard to our experimental questions. Subjects were paid $10 per hour and all had normal or corrected-to-normal vision. Subject ages ranged from 18 to 49 years. For Experiment 1, a full data set consisted of 512 trials (128 trials × 4 sessions) consisting of 64 repetitions in each of the 6 experimental conditions. For Experiment 2, a full data set consisted of 1024 (128 trials × 8 sessions) trials, yielding 128 repetitions for cued and uncued conditions and 256 repetitions for neutral conditions. On their first visit, subjects received verbal instructions and then completed one practice block of 128 trials.
2. 2. Stimuli and Task
Stimuli were two superimposed circular patterns of randomly-distributed dots rotating in opposite directions about a central yellow fixation spot. The rotation of one dot field was briefly interrupted by a translation, which the subjects had to judge (see below). The average density of each dot field was 5 dots per square degree of visual angle. Each individual dot subtended 0.03 degrees of visual angle (i.e. 1 pixel). Both patterns rotated 81 degrees per second about the fixation spot. Stimulus diameter was 4.0 degrees of visual angle. The fixation spot subtended 0.40 degrees of visual angle. One dot field was red (43.6 cd/m2) and the other was green (50.0 cd/m2). These luminance values were approximately equilumi-nant based on heterochromatic flicker fusion (Ives, 1912): Red luminance was held constant at 43.6 cd/m2 and subjects adjusted the green luminance until minimal flicker was reported. Experiments were conducted in a dark, quiet room. A Trinitron Multiscan E500 monitor displayed stimuli at a refresh rate of 75 Hz.
Subjects were informed that the translating dots could be of either field and hence that there was no incentive to selectively attend to one of the dot fields. They were also informed that only a subset of one of the dot fields translated coherently (see below) and were told to attend to the entire stimulus so as to maximize their ability to discriminate the global direction of those translations. Subjects were instructed to fixate throughout the trial but were allowed to respond immediately following the translation. Participants sat comfortably with head resting in a chin and forehead rest at a viewing distance of 57 cm from the computer screen. At the beginning of each trial, the yellow fixation spot appeared in the center of the screen. Once confident of fixation, subjects initiated a trial by key-press.
2. 3. Experiment 1
Figure 4 illustrates the 6 stimulus conditions of Experiment 1. Half of the trials in Experiment 1 had delayed onset of one of the two dot fields and half had common onsets. Delayed onset trials began with a 750-millisecond period during which one dot field appeared and continuously rotated about the fixation point, after which a counter-rotating dot field appeared superimposed on the original dot field and both continued to rotate for 300 ms. Following this period of dual rotation, either the delayed dot field translated briefly (40 ms) in one of eight directions (a “cued” translation) or the non-delayed dot field translated (an “uncued” translation). Observers reported the perceived translation direction by pressing the appropriate key on a numeric keypad.
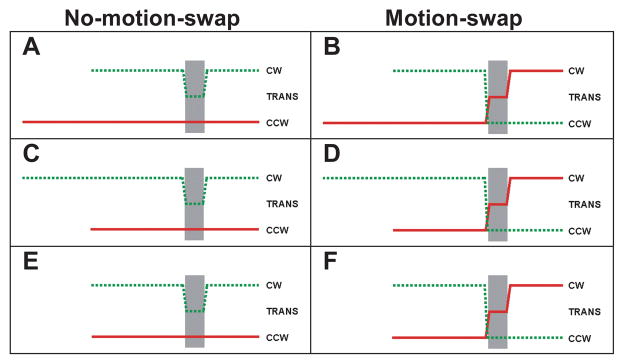
Figure 4.
Feature trajectories of dots in Experiment 1 following conventions of Figures 1B and 2B. Left Column (A, C, and E): Stimuli without motion swaps. Right Column (B, D, and F): Stimuli with motion swaps. At translation onset the other dot field adopts the other dot field’s rotation direction. This manipulation reverses the relationship between cueing and motion duration for stimuli with delayed onset of one of the dot fields. We refer to stimuli with common onsets (bottom row, E and F) as the neutral condition. For stimuli with delayed onset (A-D), the interval between onsets is 750 ms. The interval between onset of the 2nd dot field (or simultaneous onsets for E and F) and the translation is fixed at 300 ms. Following the brief translation (40 ms), both dot fields rotated for 500 ms.
As seen in Figure 4, during the translation period, the non-translating dot field either continued to rotate in its original direction (“No-motion-swap” trials) or reversed direction thereby assuming the translating dot field’s previous direction of rotation (“Motion-swap” trials). It kept this motion until the end of the trial. After the translation, the translating dot field either resumed its original rotation direction (“No-motion-swap” trials) or assumed the other dot field’s pre-translation rotation direction (“Motion-swap” trials). The post-translation rotation duration was 500 ms.
In common-onset trials, the initial 750-millisecond single-field rotation period was omitted. This condition provided a yardstick by which to measure the effect of cueing (i.e. delayed onset). It also allowed us to assay the effect of motion swaps independent of delayed onset. Since neither dot field has a cueing advantage, we refer to this condition as “neutral”.
Following Valdes-Sosa et al. (2000), only a subset of the dots translated coherently and the motions of the remaining dots were distributed equally in the other 7 directions. The percentage of coherently moving dots varied randomly from 40% to 55%. All dots translated at a speed of 2.26 degrees of visual angle per second. Translation duration was held constant at 40 milliseconds (3 frames at 75 Hz). Different random-dot patterns were used for every translation direction.
2. 4. Experiment 2
Experiment 2 was identical to Experiment 1 except that common-onset trials were omitted and replaced by color-swap trails: on half of the trials, the colors of the two dot fields were swapped at the beginning of translation. Rotation and color swaps were implemented independently (Figure 5). We increased the number of trials in Experiment 2 (by doubling the number of sessions) to get a more reliable estimate of performance.
Figure 5.
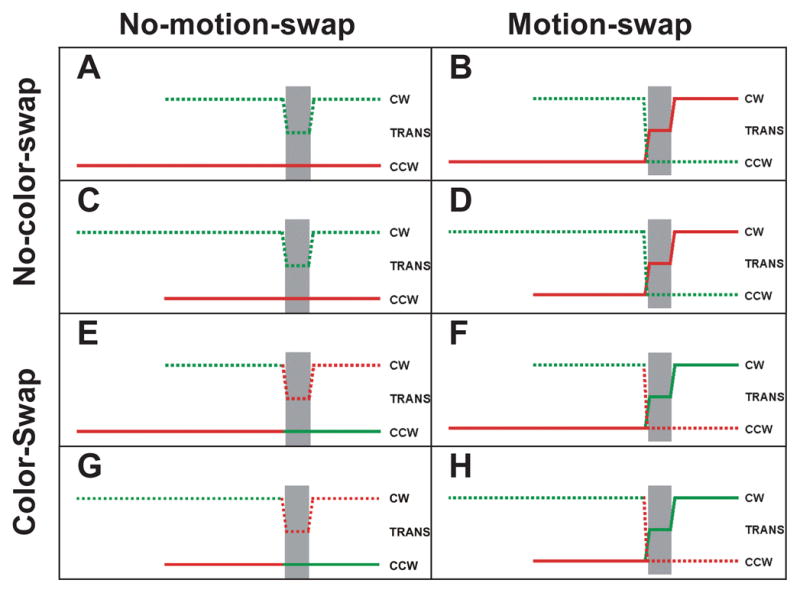
Feature trajectories of dots in Experiment 2 following conventions of Figures 1B and 2B. Left Column (A, C, E and G): Stimuli without motion swaps. Right Column (B, D, F and H): Stimuli with motion swaps. Top Two Rows (A, B, C and D): Stimuli without color swaps. Bottom Two Rows (E, F, G and H): Stimuli with color swaps. Timing is same as in Figure 4.
2. 5. Analyses
For both Experiments, pair-wise comparisons were made between all condition pairs using Liddell’s Exact test (Liddell, 1978), a proportions statistic utilizing the binomial distribution to ascertain significance for non-normally distributed data. Whether performance for individual conditions was above chance was also determined using this test and provided a criterion for the inclusion of subjects in our study (see Observers).
Data were also analyzed with repeated-measures ANOVA. For Experiment 1, there were two factors: 1) cueing (i.e. whether the translating dot field was delayed or non-delayed), and, 2) motion duration (i.e. whether the translation occurred in the presence of an old or a new rotation direction). Note that “cueing” applies to the dot field as defined by the spatio-temporal continuity of dots from one frame to the next. In the Discussion, we consider the possibility that the visual system might have instead defined the dot fields based on the global attributes of these stimuli (i.e. rotation direction and/or color).
Since neutral conditions did not differ in these two factors, they were not included in the ANOVA and were only analyzed using Liddell’s Exact Test. For Experiment 2, we added a third factor and used a three-way repeated-measures ANOVA (Trujillo-Ortiz, Hernandez-Walls, & Trujillo-Perez, 2006): 3) color duration (i.e. whether the translating dots themselves were of the old or new color). There were two levels for all of these variables and the values of these variables for the different conditions of Experiments 1 and 2 are shown in Tables I and II respectively. Note that motion duration refers to the non-translating dots, whereas color duration refers to the translating dots. This labeling reflects the different mechanisms proposed to be engaged by these two factors but has no impact on our analyses. To reiterate, the key factor for the motion-competition explanation is the adaptation state of the neurons responding to the rotation of the non-translating dot field. Conversely, the key determinant for the color-adaptation explanation is the adaptation state of the neurons responding to the color of the translating dot field (See Discussion).
Table 1.
Levels of Cued-Uncued and New-Old Motion ANOVA factors used to analyze delayed-onset conditions (i.e. excepting common-onset conditions) from Experiment 1 (compare with A-D in Figure 4). The relationship between Cueing and Motion duration (of the “competing rotation”) are reversed in the top versus bottom rows. See Analyses.
| A | B |
|---|---|
| Cued | Uncued |
| Old Motion | Old Motion |
| C | D |
| Uncued | Cued |
| New Motion | New Motion |
Table 2.
Levels of Cued-Uncued, New-Old Motion, New-Old Color ANOVA factors used to analyze results from Experiment 2 (compare with A-H in Figure 5). See Analyses.
| A | B |
|---|---|
| Cued | Uncued |
| Old Motion | Old Motion |
| New Color3 | Old Color3 |
| C | D |
| Uncued | Cued |
| New Motion | New Motion |
| Old Color3 | New Color3 |
| E | F |
| Cued | Uncued |
| Old Motion | Old Motion |
| Old Color3 | New Color3 |
| G | H |
| Uncued | Cued |
| New Motion | New Motion |
| New Color3 | Old Color3 |
2. 6. Model Predictions
Before examining our experimental findings, we apply our model to stimuli with and without “motion-swaps”. We do this to support our assertion that the motion-competition account predicts that motion swaps should yield a reversal in the magnitude of responses to the translation and by inference a reversal in psychophysical performance.
The predicted reversal in response magnitude assumes that the level of adaptation of the neurons responding to the surviving rotation during a translation of the uncued field in a motion-swap trial (Figure 4B) would be qualitatively the same as during a translation of the cued dot field in a no-motion-swap trial (Figure 4A). Likewise, the level of adaptation should be qualitatively the same during cued translations in a motion-swap trial (Figure 4D) as during uncued translations in a no-motion-swap trial (Figure 4C). This equivalency in turn follows from the assumption that the level of adaptation of a direction-selective neuron depends on the motion history within its receptive field independent of which dots undergo those motions. In conjunction with motion competition, this assumed equivalency in adaptation level leads to the prediction that, for motion-swap trials, uncued translations should yield smaller responses (from neurons selective for those translations) than cued translations. In consequence, uncued trials should be easier to discriminate than cued translations.
In the modeled responses shown in Figure 3, the motions had binary values (either present or absent). Here, we allow for the variation in motion strength that follows from the random placement of individual moving dots within receptive fields (RFs) that are smaller than the entire stimulus. We generated 100 stimuli with the same statistics as those in our psychophysical experiments and determined the motions present within circular RFs of different sizes. As an estimate of the strength of each direction of motion within a RF of a given size, we simply counted the number of dots moving in a given direction that fell within a circle of a given radius. We then normalized these values to a maximum of 50 (to agree with the modeling exercise in the Introduction). We first examined responses of model neurons with RFs large enough to include all dots of these stimuli (i.e. at minimum a RF centered at fixation with a diameter of 4 degrees). For these RFs, we assume that the adapting responses to the rotations were from rotation-selective neurons. We also examined the responses of neurons with smaller RFs: diameters of 2, 1, 0. 5, and 0.25 degrees. These latter RFs were centered 1 degree to the right of fixation. The adapting responses in these later cases were assumed to be from neurons selective for the translational component produced by rotation within that neuron’s RF. Such neurons would be stimulated by downward motion in the presence of clockwise rotation and upward motion in the presence of counter-clockwise rotation. Thus the responses to the rotations shown in Figure 3A and B could be viewed as being either from neurons selective for rotation direction (as are found in cortical area MST) or from neurons selective for translation direction (as are found in cortical areas V1, V2, MT and MST). The motion-competition account is consistent with either type of selectivity.
For the larger RF sizes (i.e. 4 and 2 degree diameters), we found that the simulated responses to the brief translations (to be concrete, we assume that they were rightward) matched those found when we assumed binary input values: cued responses were, on average, 20–21% greater than to uncued conditions. Conversely, for the key motion-swap condition, we found that the uncued condition always yielded the larger average responses – again 20–21% greater than cued conditions. All of these response asymmetries were highly significant (p < 0.001, paired t-test). These RF sizes are consistent with those found in areas MT and MST.
The above response biases begin to break down for smaller RFs. This is because smaller RFs do not always contain dots from both dot fields and hence do not become as adapted as neurons with larger RFs. Thus, for a RF size of 1 degree, the same qualitative trend held but the response bias dropped to ~16% (p<0.001). The bias is yet smaller for smaller RFs so that for the smallest RF tested (0.25 degrees), the bias for cued versus uncued becomes insignificant. This size of RF is consistent with area V1 (Gattass, Gross, & Sandell, 1981; Burkhalter & Van Essen, 1986.). These results demonstrate that our motion-competition model: 1) accounts for the original bias found with the delayed-onset design, 2) predicts a reversal in the response bias for motion-swap trials, and 3) is consistent with the properties of areas MT and MST, but not area V1.
In addition to the above key conditions, we also examined the motion-competition model’s responses to neutral (common-onset) conditions with and without motion swaps. We found that neutral conditions elicited translation responses that were, on average, significantly smaller than both cued and uncued conditions (all p < 0.001 for RF sizes > 0.5). This result follows from the fact that both rotations are, in effect, delayed for the common-onset trials so that responses to neither rotation are very adapted during the translation. Hence inhibition (which is simply the sum of the rotation responses) is greater for neutral than for cued and uncued conditions. We found no consistent bias in the responses to neutral conditions with motion swaps versus those without.
3. Results
3.1. Experiment 1
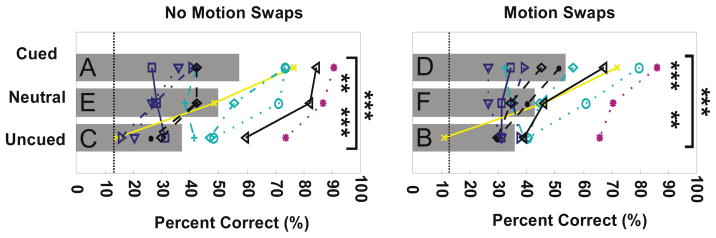
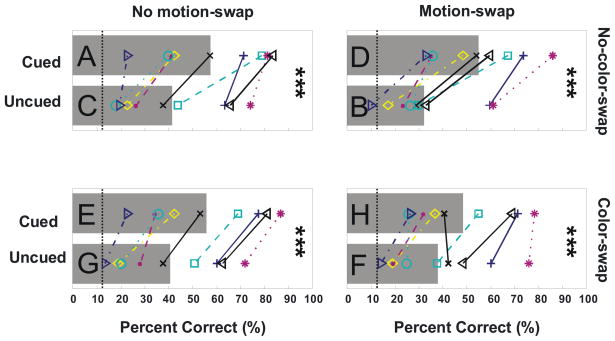
Figure 6 illustrates the results of the 6 conditions of Experiment 1 with left and right columns showing no-motion-swap and motion-swap conditions respectively. Bars indicate averaged data, with letter labels corresponding to the stimulus conditions shown in Figure 4 and Anova Factors shown in Table 1. Individual subject data are shown by line graphs. In agreement with Reynolds et al. (2003), we found that observers were, on average, significantly better at judging translations of the cued (delayed) dot field than of the uncued (non-delayed) dot field (A vs. C; Liddell’s Exact test, p < 0.001; see Methods). This trend held for all but 2 observers who showed little bias in performance. Note that this bias was seen for subjects with very different levels of overall performance. Under these stimulus conditions, cued translations occur in the presence of the older direction of rotation, whereas uncued translations occur in the presence of the newer rotation direction. Thus, while these data are compatible with the surface-based selection hypothesis, they are also compatible with the motion-competition hypothesis.
Figure 6.
Results of Experiment 1. Individual subject performance is shown by conjunctions of color, line style, and symbols. Mean accuracy across 11 subjects in reporting the direction of the translation in the 6 conditions of Experiment 1 is shown by bars. Each bar is the average of all subject’s performance for a given condition. Letter labels indicate stimulus conditions and correspond to those in Figure 4. For all condition types, cued trials yielded significantly better performance than uncued trials (p<0.001). Asterisks indicate significance level for pair-wise comparisons (2 and 3 asterisks corresponding to p<0.01 and p<0.001 respectively). Chance performance is 12.5% (dotted lines).
Our model predicted that the neutral condition would elicit performance that was worse than either cued or un-cued conditions. Contrary to that prediction, the neutral condition yielded performance that was intermediate to cued and uncued conditions. Performance for that condition was significantly less than for cued trials (E vs. A; Liddell’s Exact test, p<0.01) and greater than for uncued trials (E vs. C; Liddell’s Exact test, p<0.001). Therefore, relative to this condition, delayed onset both enhanced the ability to discriminate translations of the delayed dot field and decreased the ability to discriminate translations of the non-delayed dot field.
Figure 6 (right) shows data from the key novel conditions in which non-translating dot fields reversed rotation direction at the onset of the translation (Figure 4, right). For these motion-swap conditions, cued translations occur in the presence of the newer rotation direction, and uncued translations occur in the presence of the older rotation direction. As discussed above, our motion-competition model predicts that the performance bias should reverse relative to that seen for the no-motion-swap conditions (Figure 6, left): performance should be better when the non-delayed dot field translated rather than when the delayed dot field translated. Contrary to that prediction, performance again significantly favored translations of the delayed dot field (D vs. B; Liddell’s Exact test, p<0.0001).
We also compared performance in the neutral condition with and without motion swaps. This comparison provides an assay of the effect of motion swaps isolated from the effect of delayed onset. This comparison revealed that performance on trials without motion swaps were significantly greater than for trials with motion swaps (E vs. F; Liddell’s Exact test, p<0.001). Thus motion swaps slightly disrupted overall performance. Our model did not exhibit that disruption.
Analysis of the four cued and uncued conditions (2-way repeated-measures ANOVA, with cueing and motion duration as factors; neutral conditions were not included; See Methods) confirmed that motion duration had no significant effect on performance (p=0.5375) and that cueing was the primary determinant of performance (p<0.001). No significant interaction was found between cueing and motion duration (p=0.3844). Taken together, these results argue strongly against the motion-competition explanation: the relative “newness” of the motions competing with the translation does not account for the performance differences.
3.2. Experiment 2
The results of Experiment 1 demonstrated that motion-duration did not predict performance but did not rule out a role for color duration. As noted in the Introduction, previous studies have found cueing effects in the two-translation design in which color duration differences are absent (e.g. Valdes-Sosa et al. 2000; Reynolds et al. 2003) and when the two dot fields were the same color (Mitchell et al. 2003). Color duration cannot therefore account for the performance bias found in the two-translation design. These previous findings do not, however, rule out the possibility that color duration might contribute to the effects seen in the delayed-onset design where color duration differences are present.
In Experiment 2, we asked whether color duration played a role in the delayed-onset design. To accomplish this, we introduced color swaps at translation onset on some trials either with or without motion swaps (Figure 5). This also allowed us to confirm the results of Experiment 1 and to look for interactions between color and motion. The letter labels in Figure 7 correspond to the stimulus conditions shown in Figure 5.
Figure 7.
Performance data for the 4 conditions of Experiment 2. Data from each subject is distinguished by a unique conjunction of color, line style and symbol. Data from the two subjects that also ran in Experiment 1 are portrayed in the same way as in Figure 6 (Black upside-down triangles and Magenta asterisks). Each bar is the average of all subject’s performance for a given condition. Letter labels indicate stimulus conditions and correspond to those in Figure 5. For all condition types, cued trials yielded significantly better performance than uncued trials (p<0.001). Chance performance is 12.5% (dotted lines).
As can be seen by comparing Figure 7 with Figure 6, the results of Experiment 2 agree with those of Experiment 1: Performance was significantly better when the cued dot field translated both in the absence of motion swaps (A vs. C; Liddell’s Exact test, p<0.001) and in presence of motion swaps (D vs. B; Liddell’s Exact test, p<0.001). The effect of cueing on performance also held in the presence of color swaps: Performance favored translations of the cued dot field on color-swap trials both in the absence (E vs. G), and in the presence (H vs. F) of motion swaps (Liddell’s Exact test, all p<0.001). With the exception of 2 subjects under the combined motion- and color-swap condition, this bias in favor of cued translations held for all subjects and all conditions. This bias again held for subjects with very different overall levels of performance. Thus delayed onset does not primarily affect performance in the delayed-onset design by introduction of motion or color duration differences.
While the above analyses confirmed that color duration was not the primary determinant of performance, they did not rule out a contribution from color duration. To further examine the role of color we analyzed these data with a three-way repeated measures ANOVA (with cueing, motion duration, and color duration as factors, see Table II and Methods). We found, in agreement with the results of Experiment 1, that performance was mostly determined by cueing (mean performances, p<0.0001) with no significant contribution from motion duration (mean performances, p=0.8152). Color duration, however, had a significant influence on performance (mean performances, p=0.0196). The magnitude of the performance bias due to color duration was quite small relative to that due to cueing: averaging over all subjects for experiment 2, average performance was 7% better when the translation was of dots having the “new” color versus of the “old” color. In comparison, on average subjects did 43% better when translations were of the delayed dot field relative to translations of the undelayed dot field. Therefore, color duration does impact performance in the delayed-onset design but this impact is very small relative to that of cueing by delayed onset.
Finally, motion duration and cueing showed a marginally significant interaction (p=0.0503). Given that this interaction was nowhere near significant in Experiment 1 (p=0.3844), we refrain from speculating about the potential importance of this interaction. None of the other interactions (2- or 3-way) neared significance.
4. General Discussion
We have argued previously (Reynolds et al. 2003; Mitchell et al. 2003; Mitchell et al. 2004) that the Valdes-Sosa et al. (2000) design is superior to other related designs (e.g. Duncan, 1984; O’Craven et al., 1999; Blaser et al. 2000) in its ability to rule out spatial and feature-based selection. However, in attempting to understand the neuronal mechanisms that underlie the neurophysiological and performance biases found with this design, we realized that these biases were consistent with an account that does not invoke surface-based selection but instead follows from the established neuronal properties of adaptation and motion competition. The results from our current study refute that alternative account. In what follows we discuss the implications of our findings and their relation to previous research.
4.1. Ruling out motion-based competition as the explanation
As outlined in the Introduction, we realized that a simple model incorporating short-term adaptation and competition between motion stimuli could account for previous findings using the delayed-onset (Figure 1) and the two-translation version (Figure 2) of the Valdes-Sosa et al. design. We tested this motion-competition model’s predictions as they applied to the delayed-onset design.
Our model predicted that the ability to discriminate the direction of the brief translation in this design depends upon the relative durations of the rotations. Specifically, the model predicted that performance should be better if the rotation that “competed” with the translation was the older rather than the newer rotation independent of which surface was “cued” by delayed onset. In Experiment 1, we tested this prediction by reversing the rotation direction of the non-translating dots during the translation (i.e. “motion-swap” trials), thereby reversing the relationship between motion duration and which set of dots was “cued” by delayed onset. We found no significant effect of motion-duration in Experiment 1. The results of Experiment 2 confirmed the findings of Experiment 1 while also demonstrating that color duration could not account for the performance biases accompanying delayed onset. Our results thus refute the motion-competition model and more generally demonstrate that neither motion nor color duration play a definitive role in determining psychophysical performance. These results instead offer support for a surface-based account in which stimulus selection is specific to the individual texture elements that define the selected surface.
4.2. The role of color in surface-based selection
The main focus of this study was on the role of motion duration in producing the performance effects seen in the Valde-Sosa et al. design. Color duration was a secondary concern since it does not vary in the two-translation version of this design. Moreover, Mitchell et al. (2003) found that the psychophysical effect survived removal of the color differences in the two-translation version of the design. The results of Experiment 2 confirmed that color duration is not responsible for the cueing effect in the delayed-onset design but did reveal a small color effect on psychophysical performance. This effect was, however, quite small compared to the cueing effect of delayed onset.
The small color-dependent effect we observed might be explained by adaptation of color-selective neurons that provide input into motion-selective neurons. According to this scheme, neurons selective for the non-delayed color are more adapted than neurons selective for the delayed color and hence provide weaker input to neurons that respond to the translation. Another, non-mutually exclusive, possibility is that the delayed onset acts as an exogenous cue to the delayed color resulting in an increase in the gain of color-selective neurons (Mitchell et al. 2003): Although Mitchell et al. (2003), found no evidence for either mechanism in the two-translation design, one or both mechanisms could nevertheless make a small contribution in the delayed-onset design.
Although our findings do not reveal a substantial role for color-based mechanisms in the motion judgments analyzed here, they do not imply that the color of the cued (i.e. delayed) dot field is not itself preferentially processed. Indeed, if selection is of the surface as a whole (as supposed by surface- and object-based accounts), then the color as well as the motion of the selected surface should enjoy a processing benefit. Recently Fallah et al. (2007), using the delayed-onset design, have in fact documented a color-specific benefit in the responses of individual color-selective neurons within cortical area V4. The findings of Fallah et al. support the notion that all attributes of the delayed dot field are preferentially processed. Our new results taken together with those of Fallah et al. suggest that a color processing benefit should extend to a cued dot field even if it suddenly changed color.
4.3. How is selection maintained over unpredictable changes in surface attributes?
The surface-based account of the Valdes-Sosa et al. design assumes that all features of the selected perceptual surface are preferentially processed. What distinguishes the Valdes-Sosa et al. design from related designs is that selective processing is believed to embrace a new and unpredictable feature: selection must be maintained when a cued surface translates in an unpredictable direction. The surface-based account thus appears to assume that the translation is somehow dynamically “bound” with one of the rotations that preceded it. In contrast, our motion-competition model does not invoke binding: successive motions simply activate neurons with appropriate receptive field properties without regard to object of origin. Our refutation of that model thus re-raises the question of how such binding might occur.
Color is one plausible candidate to mediate such binding but Mitchell et al.’s results and our new findings (see above) rule out a decisive role for color. Prior to the current study, we had considered two other means by which this hypothetical binding might occur. First, binding could be based on the spatiotemporal continuity of the dots of the two fields. Our classification of translations as cued versus uncued (Tables 1 and 2) assumed this mechanism: a translation was defined as cued if the translating dots were originally of the delayed dot field, and as uncued if those dots were originally of the non-delayed dot field (see Analyses). Alternatively, rotation-translation binding might be based on the rotational continuity of the non-translating surface: since one direction of rotation continues during the translation, the translation could be inferred to be of the surface that had previously rotated in the other direction.
These two binding mechanisms are distinguished in that the first is grounded in the individual texture elements (i.e. dots) that define the two perceptual surfaces whereas the second is based on the “global” motion properties of those surfaces without regard to which dots possess those properties. These two mechanisms offer distinct predictions as to the effect of motion swaps. The first mechanism (spatiotemporal continuity) predicts that translations of delayed dot fields should be better discriminated than translations of the non-delayed dot field even on trials with motion (and/or color) swaps. Our results support this prediction. The second proposed mechanism (rotational continuity) makes the same prediction as the motion-competition model: motion swaps should result in performance reversals such that performance should be better on trials we classified as uncued relative to translations classified as cued. This is because translations would be bound with the rotation that was no longer present (even though the translating dots had actually previously rotated in the other direction). Since we did not find such reversals, our findings rule out both the motion-competition account and a surface-based account in which binding is based on rotational continuity. Instead, our results support a surface-based account in which binding between attributes at different points in time is achieved by selective processing of the texture elements that define each surface.
4.4. Dynamic spatial selection and the involvement of lower-order cortical areas
While spatial superimposition of the two moving dot fields rules out selective processing of a fixed location, our findings reveal that stimulus selection in this design is, at least in part, spatially specific at the scale of the moving dots that define the dot fields. At first glance, one plausible explanation of our new findings is that subjects attentionally tracked individual dots of the delayed dot field. We think this is very unlikely for several reasons. First, there was no incentive to attend to the dots of one field versus the other: the dots of the two fields were equally likely to translate and subjects were aware of that fact. Second, only a subset of the translating dots (~50%) translated coherently, so tracking individual dots is a poor strategy. Subjects were aware of this fact as well. Third, subjects were explicitly told not to attend to individual dots and told rather to distribute attention throughout the display. Fourth, upon debriefing, all of the subjects in this study (including the two authors) confirmed that they had spread their attention throughout the entire display and had never been consciously aware of tracking dots. Rather than revealing an intentional strategy of dot tracking, we hypothesize that our findings reveal an implicit process that dynamically identifies locations in the visual image that currently have the attributes of a selected stimulus. This conclusion is consistent with a recent study (Andersen, Müller, and Hillyard, 2009) that found that attention to a given feature (color in their study) in transparent-motion displays can be achieved without explicit dot tracking. We next outline our thoughts on the mechanisms that might underlie this process and how those mechanisms would support surface-based selection.
All ERP studies using the Valdes-Sosa et al. design (or variants thereof) have reported modulation of the N1 component, which is consistent with a role for the middle temporal complex (MT+). Our new results, however, demonstrate a degree of spatial specificity that is greater than that expected of areas MT and MST. This spatial specificity is consistent with the involvement of cortical areas with smaller receptive fields such as V1 and V2. Given our findings, it is intriguing to note that recently Khoe et al. (2005), using the two-translation design, found modulation of an earlier (C1) component, generally associated with a striate origin but potentially consistent with extrastriate areas such as V2.
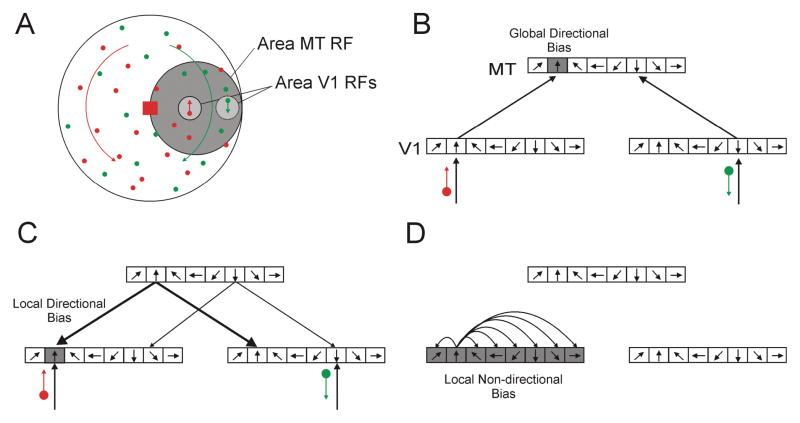
Based on our findings, and those of Khoe et al., we speculate that the surface-based effects documented here occur via interactions between MT (and/or MST) and V1 (and/or V2). We propose 3 computational steps by which an initial direction-specific processing advantage within area MT could be transformed into a spatially-specific advantage within area V1:
-
“Global” direction-specific enhancement within area MT.
Area MT neurons, just prior to translation, respond more to the motion of the delayed dot field than to the non-delayed dot field. This results in a direction-specific bias at the spatial scale of the entire stimulus.
-
Local direction-specific enhancement within area V1.
Area V1 receives feedforward input from the lateral geniculate nucleus and feedback input from area MT. We assume that these inputs interact non-linearly so that the total activation within a hypercolumn is greater when the feedback and feedforward input are to the same neurons.
-
Local non-direction-specific enhancement within area V1.
Facilitated neurons in area V1 spread facilitation via lateral interactions to other neurons within their hypercol-umn. This results in enhanced responses to any direction of motion within this facilitated hypercolumn. This spatially-local processing advantage is then presumed to be passed on to higher-order areas such as MT.
These 3 computational steps are illustrated in Figure 8. Note that these hypothetical steps are not, strictly speaking, sequential since feedforward, feedback, and lateral connections are continuously interacting. As discussed in Methods (2.6., Model Predictions), the rotations have a local translation component and we assume that area V1 and MT neurons are responding to these components. For the RFs illustrated, clockwise and counterclockwise rotations yield downward and upward translations respectively.
Figure 8.
Schematic of hypothetical selection mechanism. A) Transparent-motion stimuli. Dark and light gray circles indicate examples of neuronal receptive fields (RFs) for areas MT and V1, respectively. The MT RF is stimulated by both dot fields, whereas the two V1 RFs are stimulated by dots from different fields. B-D illustrate 3 computational steps proposed to occur just before (B-C) and during (D) translation. Illustrated are the directional hypercolumns within areas MT (top) and V1 (bottom) that have the RFs indicated in A. Grey columns have a processing advantage. B) First computational step. Feature selective processing at a coarse spatial scale. Upward-preferring neurons in area MT have a processing advantage. This advantage might result from adaptation (see Introduction and Figure 3) or from top-down feature-specific inputs. This confers a “global” (i.e. at the scale of MT RFs) processing advantage for upward motion. C) Second processing step. Feedback from area MT onto area V1 connects neurons with similar direction preferences. Convergence between more activated feedback connections (thicker lines) and feedforward input yields an advantage for upward-preferring neurons with RFs containing upward-moving dot. This directional advantage is thus spatially restricted to dots of the cued field. D) Third processing step. Local connections spread facilitation within V1 hypercolumn. This leads to enhanced processing of any direction of motion within the collective RF of the hypercolumn.
In the 1st step (Figure 8B) MT neurons that respond to the newer (i.e. delayed) rotation are, just prior to the translation, more active than those responding to the older (non-delayed) rotation. In the case of the delayed-onset and two-translation paradigms discussed here, this response bias is fully consistent with single-unit studies demonstrating short-term adaptation (e.g. Priebe, Lisberger, & Churchland, 2002; Priebe & Lisberger, 2002; Duffy & Wurtz, 1997; see Figure 3). This response bias could also be the result of top-down feature-specific input onto area MT as revealed by single-unit studies of attentional modulation in area MT (e.g. Treue and Martinez-Trujillo 1999; Martinez-Trujillo and Treue, 2004).
The 2nd step (Figure 8C) assumes that MT neurons send feedback connections to neurons in area V1 (and/or V2) having a shared directional preference. Neuroanatomical studies in the squirrel monkey are broadly consistent with this type of specificity (Rockland and Knutson, 2000). Furthermore, single-unit studies suggest that MT feedback onto V1 interacts with feedforward input so as to boost motion-selective responses in area V1 (Bullier, Hupe, James, and Girard, 2001). We thus predict that neurons in area V1 that are responding to motion of the cued dot field would be more active than neurons responding to the other rotation direction. This second step transforms the direction-specific advantage within area MT, which applies to the whole stimulus, to a directional advantage specific to the location of the dots of the delayed dot field. This advantage is thus both direction- and location-specific.
The 3rd step (Figure 8D) is the most critical of our proposal. In the context of the experimental design studied here, it applies to the point-in-time at which the rotation changes to a translation. This step transforms the direction-specific advantage achieved by the 2nd step into a non-direction specific facilitation of neurons with RFs that contain dots moving in the advantaged direction. We speculate that this step is accomplished by short-range cortical connections. Whereas longer-range horizontal connections are thought to connect neurons having similar stimulus preferences (Gilbert and Wiesel, 1989), local connections appear to be less specific (Das and Gilbert, 1999; Buzás, Kovács, Ferecskó, Budd, Eysel, and Kisvárday, 2006; Bosking, Zhang, Schofield, and Fitzpatrick, 1997; Malach, Amir, Harel, Grinvald, 1993). Since these local connections connect neurons with overlapping spatial receptive fields, a V1 neuron that was facilitated by feedback input would be expected to spread that facilitation to neurons with overlapping RFs but with different stimulus selectivities. In consequence, neurons activated by the 2nd step would facilitate nearby neurons within the same directional hypercolumn. This would result in a processing advantage for any translation activating that hypercolumn immediately after the rotation. Assuming that a dot from the cued field is still within the collective RF of the advantaged hypercolumn, this mechanism would confer a surface-specific processing advantage. This speculative account does not invoke competition and hence the relative durations of the rotations that compete with the translation do not matter. As such, this account is consistent with our findings, which found no significant contribution from the duration of the rotations. Given however that both neuronal adaptation and competitive interactions have been reported in areas MT and MST (which motivated our motion-competition model), there is a need to reconcile our new findings with the response properties of those areas.
4.5. Selective processing of objects in natural scenes
The Valdes-Sosa design captures several properties of natural scenes which, in concert, defeat selection mechanisms that are purely spatial or purely feature-based. First, different objects are often spatially intermingled in their projection upon the retinae. Second, the locations in the image that contain parts of an object can shift rapidly due to motions in the environment or of the eyes. Third, objects can change their attributes unpredictably.
Imagine, for example, walking through tall swaying grass and spotting a leopard moving slowly towards you. As you and/or the leopard move, some spots of the leopard disappear behind grass whereas other spots pop into view. Assume further that the leopard is well-matched in color and texture relative to the surrounding grass. How could you best detect a sudden attack by the leopard? Pooling all of the motion signals within the visual image outlined by the leopard is a poor strategy as it would yield a motion estimate that was contaminated by spurious signals from the swaying grass. Ideally, you would like to selectively pool information from only those locations at which the leopard is visible at a given moment in time. The mechanism we have outlined suggests how this might be achieved.
Although we have illustrated how this hypothetical mechanism could operate within a directional hypercolumn, the local spreading of facilitation (step 3, Figure 8D) could extend to neurons with other types of selectivity such as color. Such cross-attribute spreading would account for the color-specific processing benefit reported by Fallah et al. (2007) and more generally produce selective processing of all the attributes of a selected object. This mechanism may account for a previous report of implicit attentional selection based on spatiotemporal localization (Melcher, Papathomas, & Vidnyán-szky, 2005) as well as for recently observed single-unit correlates of surface-based attention in area MT (Wannig, Rodríguez & Freiwald, 2007). Finally, we should note that the speculative account advanced here differs from other accounts of feature-binding (e.g. Ship, Adams, Moutoussis, & Zeki, 2009) in that it does not rely on neurons tuned along multiple feature dimensions.
5.0. Conclusions
We have found that the performance bias seen in the Valdes-Sosa et al. design is not explained by the motion duration differences that distinguish cued and uncued conditions. Our results argue against a motion-competition account of that design and instead provide evidence of surface-based selection that involves fine-grained spatial selection. We offer a speculative account of how that spatial selection might be achieved. In particular, we speculate that surface-based selection can be achieved via interactions between MT+ and lower-order cortical areas with smaller receptive fields. Investigation of these hypothetical interactions awaits future experimentation.
Acknowledgments
This research was supported by NEI grant 521852. Writing of this manuscript was supported in part by an International Visiting Research Fellowship from the University of Sydney (http://www.usyd.edu.au/research/fellowships/international_visitors.shtml)
Appendix: Motion Competition Model
The motion competition model (Reynolds et al. 1999; Krekelberg and Albright, 2005) is given by:
| (Eq. 1) |
| (Eq. 2) |
| (Eq. 3) |
E and I represent the excitatory and inhibitory drive to the modeled neuron, respectively, and R is the neuronal response. K determines the maximum firing rate. Non-zero values of σ insure that the denominator is non-zero. The Cs correspond to the 3 types of motion inputs, and the Ws are the weights given to those inputs.
The adapting responses of cortical neurons are modeled by:
| (Eq. 4) |
| (Eq. 5) |
R is firing rate and is determined by the hyperbolic ratio equation of Naka and Rushton (1966) applied to positive input values (shown within the brackets and indicated by + subscript). The Naka-Rushton equation yields a sigmoidal input-output function qualitatively consistent with cortical neurons (Wilson, 1999). Stimulus corresponds to the strength of the particular motion in question. For simulation results presented in the Introduction, we set Stimulus to have binary (i.e. either the motion is present or it is not) input values: 50 and 0 for rotations, and 25 and 0 for translations (the lower translation value accounts for the fact that dots rotate with 100% coherency whereas only 50% of dots translate coherently). For the results presented in the Methods, Stimulus was weighted by the number of moving dots within a CRF of a given size.
For simplicity we model adaptation as linear with a subtractive influence (Eq. 5). Critically, the time constant that governs how quickly neurons respond to stimulus onsets and offsets is much smaller than that which governs adaptation of those responses: τ = 20, τadapt =1000. Lastly, Wadapt determines the strength of adaptation and was set to 1.25.
These adapting responses constitute the inputs (i.e. the Cs in Eqs. 1 and 2) to a translation detector modeled by Eq. 3. This translation detector is assumed to be selective for the particular direction of a translation occurring on a given trial. In our simulations using Eq. 3, K (the maximum firing rate of the translation detector) was set to 100 and (following Krekelberg and Albright, 2005) σ was set to 1. For simplicity, we assumed that the translation input has an excitatory weight of 1, the rotation inputs have inhibitory weights of 1, and all other weights are 0. Model simulations were conducted on a Windows computer using a fourth-order Runge-Kutta routine implemented in Matlab (Wilson, 1999).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aine CJ, Harter MR. Visual event-related potentials to colored patterns and color names: attention to features and dimension. Electroencephalogr Clin Neurophysiol. 1986;64:228–45. doi: 10.1016/0013-4694(86)90171-9. [DOI] [PubMed] [Google Scholar]
- Andersen SK, Müller MM, Hillyard SA. Color-selective attention need not be mediated by spatial attention. J Vis. 8;9(6):2.1–7. doi: 10.1167/9.6.2. [DOI] [PubMed] [Google Scholar]
- Anllo-Vento L, Hillyard SA. Selective attention to the color and direction of moving stimuli: electrophysiological correlates of hierarchical feature selection. Percept Psychophys. 1996;58:191–206. doi: 10.3758/bf03211875. [DOI] [PubMed] [Google Scholar]
- Blaser E, Pylyshyn ZW, Holcombe AO. Tracking an object through feature space. Nature. 2000;9;408(6809):196–9. doi: 10.1038/35041567. [DOI] [PubMed] [Google Scholar]
- Bosking Zhang, Schofield B, Fitzpatrick D. Orientation selectivity and the arrangement of horizontal connections in tree shrew striate cortex. J Neurosci. 1997;17(6):2112–27. doi: 10.1523/JNEUROSCI.17-06-02112.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullier J, Hupé JM, James AC, Girard P. The role of feedback connections in shaping the responses of visual cortical neurons. Prog Brain Res. 2001;134:193–204. doi: 10.1016/s0079-6123(01)34014-1. [DOI] [PubMed] [Google Scholar]
- Burkhalter A, Van Essen DC. Processing of color, form and disparity information in visual areas VP and V2 of ventral extrastriate cortex in the macaque monkey. J Neurosci. 1986;6:2327–2351. doi: 10.1523/JNEUROSCI.06-08-02327.1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzás Kovács, Ferecskó Budd, Eysel Kisvárday. Model-based analysis of excitatory lateral connections in the visual cortex. J Comp Neurol. 2006;499(6):861–81. doi: 10.1002/cne.21134. [DOI] [PubMed] [Google Scholar]
- Das A, Gilbert CD. Topography of contextual modulations mediated by short-range interactions in primary visual cortex. Nature. 1999;17;399(6737):655–61. doi: 10.1038/21371. [DOI] [PubMed] [Google Scholar]
- Desimone R, Duncan J. Neural mechanisms of selective visual attention. Annu Rev Neurosci. 1995;18:193–222. doi: 10.1146/annurev.ne.18.030195.001205. [DOI] [PubMed] [Google Scholar]
- Duffy CJ, Wurtz RH. Multiple temporal components of optic flow responses in MST neurons. Exp Brain Res. 1997;114(3):472–82. doi: 10.1007/pl00005656. [DOI] [PubMed] [Google Scholar]
- Duncan J. Selective attention and the organization of visual information. J Exp Psychol Gen. 1984;113:501–17. doi: 10.1037//0096-3445.113.4.501. [DOI] [PubMed] [Google Scholar]
- Fallah M, Stoner GR, Reynolds JH. Stimulus-specific competitive selection in macaque extrastriate visual area V4. Proc Natl Acad Sci USA. 2007;104:4165–9. doi: 10.1073/pnas.0611722104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gattass R, Gross CG, Sandell JH. Visual topography of V2 in the macaque. J Comp Neurol. 1981;201:519–539. doi: 10.1002/cne.902010405. [DOI] [PubMed] [Google Scholar]
- Gilbert CD, Wiesel TN. Columnar specificity of intrinsic horizontal and corticocortical connections in cat visual cortex. J Neurosci. 1989;9(7):2432–42. doi: 10.1523/JNEUROSCI.09-07-02432.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ives HE. The relation between the color of the illuminant and the color of the illuminated object. Trans Illum Engineer Soc. 1912;7:62–72. [Google Scholar]
- Khoe W, Mitchell JF, Reynolds JH, Hillyard SA. Exogenous attentional selection of transparent superimposed surfaces modulates early event-related potentials. Vision Res. 2005;45:3004–14. doi: 10.1016/j.visres.2005.04.021. [DOI] [PubMed] [Google Scholar]
- Krekelberg B, Albright TD. Motion mechanisms in macaque MT. J Neurophysiol. 2005;93(5):2908–21. doi: 10.1152/jn.00473.2004. [DOI] [PubMed] [Google Scholar]
- Liddell D. Practical Tests of 2 × 2 Contingency Tables. The Statistician. 1978;25:295–304. [Google Scholar]
- Lopez M, Rodriguez V, Valdes-Sosa M. Two-object attentional interference depends on attentional set. Int J Psy-chophysiol. 2004;53:127–34. doi: 10.1016/j.ijpsycho.2004.03.006. [DOI] [PubMed] [Google Scholar]
- Luck SJ, Chelazzi L, Hillyard SA, Desimone R. Neural mechanisms of spatial selective attention in areas V1, V2, and V4 of macaque visual cortex. J Neurophysiol. 1997;77:24–42. doi: 10.1152/jn.1997.77.1.24. [DOI] [PubMed] [Google Scholar]
- Malach R, Amir Y, Harel M, Grinvald A. Relationship between intrinsic connections and functional architecture revealed by optical imaging and in vivo targeted biocytin injections in primate striate cortex. Proc Natl Acad Sci U S A 1993. 1993 Nov 15;90(22):10469–73. doi: 10.1073/pnas.90.22.10469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinez-Trujillo JC, Treue S. Feature-based attention increases the selectivity of population responses in primate visual cortex. Curr Biol. 2004;14:744–751. doi: 10.1016/j.cub.2004.04.028. [DOI] [PubMed] [Google Scholar]
- Melcher D, Papathomas TV, Vidnyánszky Z. Implicit attentional selection of bound visual features. Neuron. 2005;46(5):723–9. doi: 10.1016/j.neuron.2005.04.023. [DOI] [PubMed] [Google Scholar]
- Mitchell JF, Stoner GR, Fallah M, Reynolds JH. Attentional selection of superimposed surfaces cannot be explained by modulation of the gain of color channels. Vision Res. 2003;43:1323–8. doi: 10.1016/s0042-6989(03)00123-8. [DOI] [PubMed] [Google Scholar]
- Mitchell JF, Stoner GR, Reynolds JH. Object-based attention determines dominance in binocular rivalry. Nature. 2004;429:410–3. doi: 10.1038/nature02584. [DOI] [PubMed] [Google Scholar]
- Moran J, Desimone R. Selective attention gates visual processing in the extrastriate cortex. Science. 1985;229:782–4. doi: 10.1126/science.4023713. [DOI] [PubMed] [Google Scholar]
- Naka K, Rushton W. S-potentials from luminosity units in the retina of fish (Cyprinidae) J Physiology. 1996;185:587–599. doi: 10.1113/jphysiol.1966.sp008003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Craven KM, Downing PE, Kanwisher N. fMRI evidence for objects as the units of attentional selection. Nature. 1999;401:584–7. doi: 10.1038/44134. [DOI] [PubMed] [Google Scholar]
- Pinilla T, Cobo A, Torres K, Valdes-Sosa M. Attentional shifts between surfaces:effects on detection and early brain potentials. Vision Research. 2001;41:1619–30. doi: 10.1016/s0042-6989(01)00039-6. [DOI] [PubMed] [Google Scholar]
- Posner M. Orienting of Attention. Quarterly Journal of Experimental Psychology. 1980;32:3–25. doi: 10.1080/00335558008248231. [DOI] [PubMed] [Google Scholar]
- Posner MI, Cohen Y. Components of visual orienting. In: Bouma H, Bouwhuis D, editors. Attention and Performance. Earlbaum; 1984. pp. 531–56. [Google Scholar]
- Priebe NJ, Churchland MM, Lisberger SG. Constraints on the source of short-term motion adaptation in macaque area MT. I. the role of input and intrinsic mechanisms. J Neurophysiol. 2002;88:354–69. doi: 10.1152/.00852.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Priebe NJ, Lisberger SG. Constraints on the source of short-term motion adaptation in macaque area MT. II. tuning of neural circuit mechanisms. J Neurophysiol. 2002;88:370–82. doi: 10.1152/jn.2002.88.1.370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian N, Andersen RA. Transparent motion perception as detection of unbalanced motion signals. II. Physiology. J Neurosci. 1994;14:7367–80. doi: 10.1523/JNEUROSCI.14-12-07367.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Recanzone GH, Wurtz RH. Effects of attention on MT and MST neuronal activity during pursuit initiation. J Neu-rophysiol. 2000;83:777–90. doi: 10.1152/jn.2000.83.2.777. [DOI] [PubMed] [Google Scholar]
- Recanzone GH, Wurtz RH, Schwarz U. Responses of MT and MST neurons to one and two moving objects in the receptive field. J Neurophysiol. 1997;78:2904–15. doi: 10.1152/jn.1997.78.6.2904. [DOI] [PubMed] [Google Scholar]
- Reynolds JH, Alborzian S, Stoner GR. Exogenously cued attention triggers competitive selection of surfaces. Vision Res. 2003;43:59–66. doi: 10.1016/s0042-6989(02)00403-0. [DOI] [PubMed] [Google Scholar]
- Reynolds JH, Chelazzi L, Desimone R. Competitive mechanisms subserve attention in macaque areas V2 and V4. J Neurosci. 1999;19:1736–53. doi: 10.1523/JNEUROSCI.19-05-01736.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rockland KS, Knutson T. Feedback connections from area MT of the squirrel monkey to areas V1 and V2. J Comp Neurol. 2000;25;425(3):345–68. [PubMed] [Google Scholar]
- Rodriguez V, Valdes-Sosa M. Sensory suppression during shifts of attention between surfaces in transparent motion. Brain Res. 2006;1072:110–8. doi: 10.1016/j.brainres.2005.10.071. [DOI] [PubMed] [Google Scholar]
- Rodriguez V, Valdes-Sosa M, Freiwald W. Dividing attention between form and motion during transparent surface perception. Brain Res Cogn Brain Res. 2002;13:187–93. doi: 10.1016/s0926-6410(01)00111-2. [DOI] [PubMed] [Google Scholar]
- Shipp S, Adams DL, Moutoussis K, Zeki S. Feature Binding in the Feedback Layers of Area V2. Cereb Cortex. 2009 Jan 19; doi: 10.1093/cercor/bhn243. 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snowden RJ, Treue S, Erickson RG, Andersen RA. The response of area MT and V1 neurons to transparent motion. J Neurosci. 1991;11:2768–85. doi: 10.1523/JNEUROSCI.11-09-02768.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tootell RB, Reppas JB, Kwong KK, Malach R, Born RT. Functional analysis of human MT and related visual cortical areas using magnetic resonance imaging. J Neurosci. 1995;15:3215–30. doi: 10.1523/JNEUROSCI.15-04-03215.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Treisman AM, Gelade G. A feature-integration theory of attention. Cognit Psychol. 1980;12:97–136. doi: 10.1016/0010-0285(80)90005-5. [DOI] [PubMed] [Google Scholar]
- Treue S, Martinez-Trujillo JC. Feature-based attention influences motion processing gain in macaque visual cortex. Nature. 1999;399:575–579. doi: 10.1038/21176. [DOI] [PubMed] [Google Scholar]
- Trujillo-Ortiz A, Hernandez-Walls R, Trujillo-Perez FA. RMAOV33: Three-way Analysis of Variance With Repeated Measures on Three Factors Test. A MATLAB file. 2006 http://www.mathworks.com/matlabcentral/fileexchange/loadFile.do?objectId=9638.
- Valdes-Sosa M, Bobes MA, Rodriguez V, Acosta Y, Perez P, et al. The influence of scene organization on attention: Psychophysics and electrophysiology. In: Kanwisher N, Duncan J, editors. Attention and performance XX: Functional neuroimaging of visual cognition. Oxford: Oxford University Press; 2004. pp. 321–44. [Google Scholar]
- Valdes-Sosa M, Bobes MA, Rodriguez V, Pinilla T. Switching Attention without Shifting the Spotlight: Object-Based Attentional Modulation of Brain Potentials. Journal of Cognitive Neuroscience. 1998;10:137–51. doi: 10.1162/089892998563743. [DOI] [PubMed] [Google Scholar]
- Valdes-Sosa M, Cobo A, Pinilla T. Attention to Object Files Defined by Transparent Motion. Journal of Experimental Psychology. 2000;26:488–505. doi: 10.1037//0096-1523.26.2.488. [DOI] [PubMed] [Google Scholar]
- Watson JD, Myers R, Frackowiak RS, Hajnal JV, Woods RP, et al. Area V5 of the human brain: evidence from a combined study using positron emission tomography and magnetic resonance imaging. Cereb Cortex. 1993;3:79–94. doi: 10.1093/cercor/3.2.79. [DOI] [PubMed] [Google Scholar]
- Wannig A, Rodríguez V, Freiwald WA. Attention to surfaces modulates motion processing in extrastriate area MT. Neuron. 2007;24;54(4):639–51. doi: 10.1016/j.neuron.2007.05.001. [DOI] [PubMed] [Google Scholar]
- Wilson HR. Spikes, decisions, and actions: dynamical foundations of neuroscience. Oxford: Oxford UP; 1999. [Google Scholar]
- Yantis S, Jonides J. Abrupt Visual Onsets and Selective Attention: Evidence from Visual Search. Journal of Experimental Psychology: Human Perception and Performance. 1984;10:601–21. doi: 10.1037//0096-1523.10.5.601. [DOI] [PubMed] [Google Scholar]
- Yantis S, Jonides J. Abrupt visual onsets and selective attention: voluntary versus automatic allocation. J Exp Psy-chol Hum Percept Perform. 1990;16:121–34. doi: 10.1037//0096-1523.16.1.121. [DOI] [PubMed] [Google Scholar]