A Repulsive Electrostatic Mechanism for Protein Export through the Type III Secretion Apparatus

Abstract

Many Gram-negative bacteria initiate infections by injecting effector proteins into host cells through the type III secretion apparatus, which is comprised of a basal body, a needle, and a tip. The needle channel is formed by the assembly of a single needle protein. To explore the export mechanisms of MxiH needle protein through the needle of Shigella flexneri, an essential step during needle assembly, we have performed steered molecular dynamics simulations in implicit solvent. The trajectories reveal a screwlike rotation motion during the export of nativelike helix-turn-helix conformations. Interestingly, the channel interior with excessive electronegative potential creates an energy barrier for MxiH to enter the channel, whereas the same may facilitate the ejection of the effectors into host cells. Structurally known basal regions and ATPase underneath the basal region also have electronegative interiors. Effector proteins also have considerable electronegative potential patches on their surfaces. From these observations, we propose a repulsive electrostatic mechanism for protein translocation through the type III secretion apparatus. Based on this mechanism, the ATPase activity and/or proton motive force could be used to energize the protein translocation through these nanomachines. A similar mechanism may be applicable to macromolecular channels in other secretion systems or viruses through which proteins or nucleic acids are transported.

Introduction

The type III secretion apparatus (TTSA) is a multiprotein molecular machine used by many Gram-negative bacteria to dock onto the eukaryotic host cell membrane and export effector proteins to initiate infections. One such Gram-negative bacterium, Shigella flexneri, causes shigellosis in humans and is responsible for over a million deaths worldwide each year (1). The Centers for Disease Control and Prevention lists Shigella as a potential agent of bioterrorism (2).

In general, the TTSA is composed of a basal body that spans the inner and outer bacterial membranes, an external needle, and a tip (Fig. 1 A) (3). Although the atomic structure of the entire TTSA is not yet known, the three-dimensional structures of several individual components are available for different Gram-negative bacteria. For instance, the structures of EscJ (4) and EscC (5) of the basal body that are associated with the inner and outer membranes of enteropathogenic Escherichia coli were determined by x-ray crystallography. EscJ is shown to form a ringlike structure based on superhelical crystal symmetry (4). Similarly, EscC and the periplasmic domain of PrgK (the inner membrane protein of Salmonella typhimurium) are also proposed to form ringlike structures (5) based on cryo-electron microscopy (EM) data (5). In addition, the needle of the S. flexneri TTSA, which is held by the basal body and protrudes from the bacterial surface, has been modeled recently based on a 16 Å cryo-EM density map (6). The needle itself is a supramolecular complex that is formed by the assembly of ∼120 copies of a needle protein around the needle channel axis. The TTSA needle proteins share high sequence and structural similarities. All the needle protein structures solved to date have a helix-turn-helix (HTH) motif that is attributed to a conserved PxxP motif at the turn region: MxiH from S. flexneri (6), PrgI from S. typhimurium (7), and BsaL from Burkholderia pseudomallei (8). In addition, the structures of the tip proteins are also known, although the basis for their association with the needle is not known in atomic detail: IpaD from S. flexneri (9), BipD from B. pseudomallei (9), and LcrV from Yersinia pestis (10).

Figure 1.

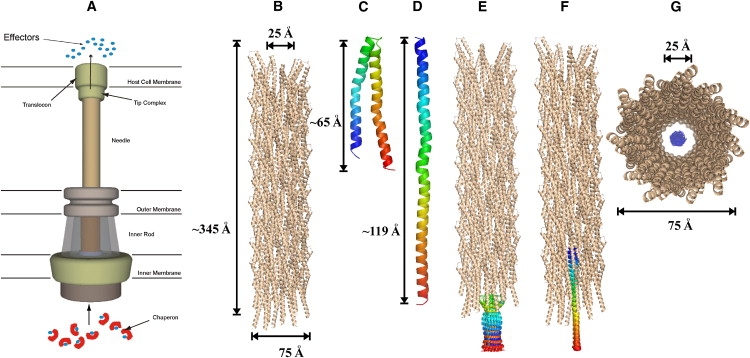
(A) Schematic representation of the TTSA. (B) Structure of the needle apparatus viewed perpendicular to the channel axis. (C and D) Two different MxiH conformations considered for the pulling simulations. (E and F) Different starting configurations used for the pulling simulation of the two-helix bundle and straight helix. (G) Perpendicular view of panel E.

The ultimate aim in these research areas is to determine the structure of the entire type III secretion nanomachine in order to understand the mechanism of effector export. Such knowledge will facilitate vaccine and drug development against these bacteria. However, understanding how proteins are exported across the TTSA poses a major challenge. In this context, we have investigated the underlying key microscopic forces responsible for protein export through the TTSA needle channel by performing steered molecular dynamics (SMD) simulations (11) to export the MxiH subunit through the needle of S. flexneri. The SMD simulations have been widely used to understand the molecular transport across biological (12,13) and nonbiological (14,15) systems. It should be noted that MxiH itself needs to be exported through the growing needle during its formation. The export of MxiH is facilitated by pulling MxiH at a constant velocity through a modeled needle channel. Because the explicit treatment of the needle and solvent makes such simulations nearly intractable, we have utilized the implicit solvent models, i.e., the generalized solvent boundary potential (GSBP) (16) to describe the mean solvent-mediated potential from the rigid needle model, and the generalized Born model with a simple switching function (GBSW) (17) to describe the solvation effects of the flexible pulled MxiH monomer. Based on the simulation results, we propose a repulsive electrostatic mechanism for MxiH transportation across the needle. We generalize this mechanism as a rationale for protein export through the TTSA based on the electrostatic surface of its components and the effectors. Furthermore, the simulation trajectories suggest that effectors may be exported through the needle apparatus in a screwlike rotation motion.

Methods

Needle apparatus modeling

A Shigella needle model was built with 64 subunits of MxiH (approximately one-half of the biological needle) (Fig. 1 B) using the biomolecular simulation program CHARMM (18). Based on the recent work of Deane et al. (6), we used the crystal structure of MxiH (PDB:2CA5) with the N-terminus facing inside the channel and the C-terminus facing the outside. In the C-terminus, the amino acids LEH were replaced with the original IQNFR sequence. The last five C-terminus residues as well as the first 19 residues of the N-terminus that were not determined in the crystal structure, were modeled as regular α-helices. Based on the helical parameters and the channel diameter of 25 Å determined by cryo-EM (6), each subunit was translated by 4.31 Å along the z axis and rotated by 64.3° around the z axis, assuming that the needle channel is parallel to the z axis. The geometric center of the needle was located at z = 0. As shown in Fig. 1, B and C, the lengths of the constructed needle and the MxiH subunit along the z axis are 345 Å and 65 Å, respectively, and the outer diameter of the needle is ∼75 Å. The inter- and intramolecular steric hindrance in the needle was removed by minimizing the entire needle with GBSW (17) in CHARMM.

SMD simulation details

To export the MxiH monomer through the needle channel (z axis), we performed SMD simulations with a constant pulling speed using a harmonic restraint potential (11). Because it is still unknown experimentally whether MxiH translocates across the needle as a folded two-helix bundle or an extended helix, we used two initial conformations of MxiH: a nativelike folded two-helix bundle with the missing N- and C-terminal regions modeled as α-helices (Fig. 1 C), and an extended α-helix (Fig. 1 D). For each system, MxiH was initially positioned outside the needle (Fig. 1, E and F). The initial z coordinates of the centers-of-mass of the two-helix bundle and straight α-helix were −164 Å and −188 Å, respectively. To examine specific rotational preference of MxiH inside the needle, we performed 18 independent pulling simulations for each system using different rotational configurations of MxiH. The configurations were generated by rotating MxiH every 20° along the z axis (Fig. 1, E and F).

The pulling speed was set to 15 Å/ns with a force constant of 150 pN/Å for the two-helix bundle and 100 pN/Å for the straight α-helix (100 pN corresponds to 1.44 kcal/(mol·Å)). A higher force constant was chosen for the two-helix bundle systems to keep the pulling spring relatively stiff, so that MxiH trajectories followed the reaction coordinate properly. In our simulations, the restraint force was applied to the center-of-mass of each MxiH monomer by modifying the AFM module (11) in CHARMM. This approach performed better than application of the force to a specific atom of the pulled MxiH monomer. The total simulation time to complete the MxiH export was ∼26 ns for the two-helix bundle and 25 ns for the extended α-helix.

Because the system size was too big for all-atom pulling simulations, we increased the computational efficiency by utilizing the implicit solvent models: the GSBP formalism (16) and the GBSW (17) (see Appendix). Based on the assumption of the rigid needle apparatus, the influence of the needle on exporting MxiH was approximated by the static electrostatic potential (${\varphi }_{\varepsilon =80}^{\text{needle}}$) from the needle as well as a repulsive core potential (U_core). The former was calculated by solving the finite-difference Poisson-Boltzmann (PB) equation using the PBEQ module (19,20) in CHARMM, and the latter was calculated by building a core repulsion potential map on a grid (see Appendix, and (21–24)). It should be noted that both electrostatic and repulsive potentials were calculated once and stored on the grids for efficient pulling simulations. Finally, the solvent effects on MxiH were treated by GBSW (17). Unless specified explicitly, all the pulling simulations were done under 150 mM salt concentration (to mimic physiological conditions) that was implicitly incorporated in both PB and GBSW calculations. Such grid-based potentials (${\varphi }_{\varepsilon =80}^{\text{needle}}$ and U_core) made the computational speed ∼45 times faster than the simulation in which all protein would be simulated explicitly with GBSW.

Results

Electrostatics of the needle channel

The electrostatic nature of the needle channel was first characterized by calculating the interaction energy between a chloride ion (Cl⁻) and the electrostatic potential from the needle (${\varphi }_{\varepsilon =80}^{\text{needle}}$) at 150 mM. As shown in Fig. 2 A, the resulting energy profile along the channel axis shows an energy barrier of ∼3 kcal/mol for Cl⁻ to enter the channel due to the electronegative potential inside the needle channel (Fig. 2 C). As expected, the repulsion increases as the salt concentration decreases due to less salt screening. The energy barrier increases from 3 kcal/mol to 10 kcal/mol when the salt concentration is decreased from 150 mM to 50 mM.

Figure 2.

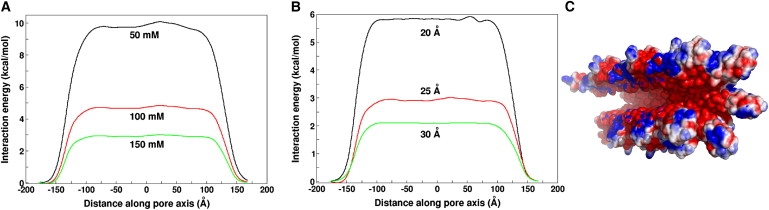
(A) Effect of different salt concentration and (B) channel radius on the energetics of Cl⁻ translation along the channel axis. (C) Cross-sectional view of the needle apparatus of S. flexneri illustrating the surface electrostatics inside the channel. For the sake of clarity, some of the needle monomers in the front are not shown. The electrostatic potentials are calculated by the PBEQ module (19) in CHARMM and visualized on the solvent-accessible surface using PyMOL (41). Electrostatic scaling used for all the figures are −0.6 (red) to 0.6 kcal/(mol·e) (blue).

Although the cryo-EM data of the needle structure reveals that the inner diameter of the channel is ∼25 Å (6), we examined the influence of different inner diameters on the electrostatic interaction by remodeling the needle with two different inner diameters (20 Å and 30 Å) (25) and recalculating ${\varphi }_{\varepsilon =80}^{\text{needle}}$ at 150 mM. As shown in Fig. 2 B, the barrier reduces as the channel diameter increases (6 kcal/mol for 20 Å to 2 kcal/mol for 30 Å). Keeping in mind such dependence of the electrostatic potential inside the needle channel, we used 150 mM with a channel diameter of 25 Å, based on the cryo-EM data in most pulling simulation studies, and used other diameters in a small number of simulations for comparison.

Tryptophan groove in the needle channel

There is a conserved tryptophan among most of the TTSA needle proteins (7), and W10 in MxiH forms a tryptophan groove inside the needle channel in our model (Fig. 3 A). This groove mimics the so-called “greasy slide” made of the aromatic residues (W, Y, and F) in maltoporin that is responsible for the sugar transport in Gram-negative bacteria (26,27). In maltoporin, in vivo sugar uptake was considerably reduced when the aromatic residues were mutated to alanines (28). Similarly, as shown in Table 1, MxiH W10 mutants show considerable differences in bacterial invasion of Henle cells and contact-mediated hemolysis of erythrocytes (see Experimental Methods in the Supporting Material). Whereas the W10Y and W10F mutants show similar phenotypes as in the wild-type, the W10A, W10H, W10R, and W10K mutants show no invasion and hemolysis upon disruption of the elongation of the needle in vivo. It should be noted that when MxiH wild-type or mutants were overexpressed in E. coli, purified in the presence of urea, and then refolded by removing the urea, the proteins formed needles in vitro (W. L. Picking, unpublished observation). This indicates that the W10 mutations do not impair the needle polymerization itself, but affect the MxiH export in vivo. The experimental results support our needle model, which has the tryptophan groove in which W10 is fully exposed in the channel interior and uninvolved in the monomer-monomer interactions. Therefore, W10 in the needle appears to have specific interactions with MxiH during its export.

Figure 3.

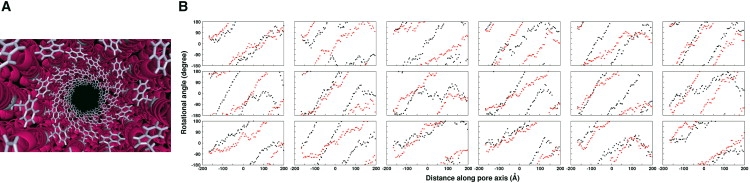
(A) View along the channel axis of the needle apparatus showing the tryptophan groove formed by W10 (colored white). (B) Rotation angle profile of MxiH two-helix bundle along the channel axis: 18 different starting positions of wild-type (black) and W10A (red).

Table 1.

Phenotypes of MxiH Trp10 mutants

MxiH	Bacterial invasion of Henle cells∗	Contact-mediated hemolysis†
mxiH null	0 ± 0	0 ± 0
MxiHWT	100 ± 1‡	100 ± 1§
MxiHW10Y	143 ± 7	104 ± 7
MxiHW10F	34 ± 4	83 ± 5
MxiHW10A	0.4 ± 1	11 ± 13
MxiHW10H	3 ± 1	4 ± 7
MxiHW10R	2 ± 1	3 ± 1
MxiHW10K	2 ± 7	11 ± 5

^∗Bacterial invasion of Henle cells is measured by using a Gentamycin protection assay to assess the ability of Shigella flexneri to invade Henle cells. The results are presented as a percentage of colonies formed relative to MxiH complemented null (pWPsf4H/SH116) mean ± SD, n = 3.

^†Contact-mediated hemolysis is measured by forcing contact of the bacteria with erythrocytes and determining the release of hemoglobin. This assay assesses the ability of the bacteria to introduce the translocon into the erythrocyte membrane. The results are presented as a percentage of hemoglobin release relative to MxiH (pWPsf4H/SH116) × mean ± SD, n = 5.

^‡Raw value of invasion of Henle cells by MxiH complemented null (pWPsf4H/SH116) is 235 ± 17 colonies.

^§Raw value of contact-mediated hemolysis of MxiH complemented null (pWPsf4H/SH116) is 3.25 ± 0.5 (A₅₄₅).

MxiH export in a screwlike rotation motion

Fig. S1 in the Supporting Material shows snapshots illustrating the transportation of the two-helix bundle across the needle. Unexpectedly, most pulling trajectories of the two-helix bundle show the export of MxiH in a screwlike rotation fashion along the needle channel (Movie S1 in the Supporting Material). Fig. 3 B quantifies such screwlike rotation by projecting a vector from Ala³⁸ Cα (before the PxxP turn motif) to Leu⁴⁷ Cα (after the motif) onto the xy plane and measuring the angle between the projected vector and the x axis. There are two noteworthy features. First, the periodicity is not regular; the rotation happens twice in some trajectories and is not complete in other trajectories, although the tendency of screwlike rotation is clearly observed. To our knowledge, this is the first report of a screwlike rotation motion as a mode of protein translocation across the needle. Second, the screwlike rotation is right-handed, which appears to be dictated by the right-handedness of the needle.

What causes such screwlike rotation during protein export along the needle channel? To examine the role of the tryptophan groove and the channel diameter in the screwlike rotation, we have performed additional pulling simulations with the W10 mutants (W10A, W10Y, and W10F) as well as with the needle of 30 Å inner diameter. We also observed similar screwlike rotation motions during MixH export (Fig. 3, Fig. S2, and Fig. S3). In contrast to the two-helix bundle, no such screwlike rotation motion is observed in the case of the straight helix (Fig. S4 and Movie S2). These results indicate that the screwlike motion may be specific for the supersecondary structures of the effectors and depend on the conformational preference of effectors as they are exported along the needle channel.

Conformational flexibility of MxiH inside the needle channel

MxiH monomers exhibited various conformational changes inside the needle during the simulations. The average helicity of MxiH two-helix bundle indicates different conformational flexibilities for the N-terminal region (residue 2–23), HTH motif (residue 20–60), and the C-terminal region (residue 57–83) (Fig. 4 A). Both terminal regions appear to be more flexible than the HTH motif. The N- and C-terminal regions exhibit ∼30% and 25% helicity, respectively. Interestingly, the flexibility observed in the C-terminal region is quite different from the well-structured helix seen in the crystal structure of the MxiH monomer. This may be attributed to crystal packing in the latter. Although individual structures show a variety of conformational preferences, which include a random coil conformation at the N-terminal region during the simulations (Fig. 4 A, Fig. S1, Fig. S5, and Fig. S6, A–C), the overall helicity of the ensemble structures clearly shows that the N-terminal region has some residual α-helical character. In fact, this observation is in accordance with the NMR data of homologous needle proteins such as PrgI and BsaL (7,8). The HTH region retains the helicity as in the initial conformation. This is again in line with the NMR data of PrgI and BsaL, implying that the residues in the HTH region have a stronger tendency to have α-helical conformations (7,8). In the case of the extended helix, both terminal regions show higher helicity (∼80% and ∼60%, respectively) (Fig. 4 B, Fig. S6, D–F), compared to the two-helix bundle. This indicates that the lower helicity (i.e., more unfolding) in the two-helix bundle may result from nonspecific interactions between the terminal regions inside the needle channel.

Figure 4.

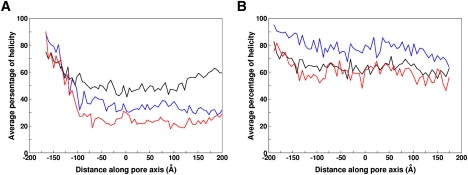
Average percentage of helicity of (A) two-helix bundle and (B) straight helix: the N-terminal region (residues 2–23: red), helix-turn-helix (HTH) motif (residues 20–60: black), and the C-terminal region (residues 57–83: blue). Helicity is measured based on the number of hydrogen bond between N−H (i) and C=0 (i+4) of backbone. A hydrogen bond (D−H⋯A) is defined by the H⋯A distance <2.8 Å and the D−H⋯A angle >120°.

Unfavorable energy barrier for MxiH export

The free energy profile of MxiH along the channel axis arguably represents a true energetics of MxiH transport, but its calculation is not trivial. Although pulling simulation trajectories have been used to calculate the free energy profile (29,30), our pulling speed (15 Å/ns) was too high, and the number of trajectories too small, to reliably calculate the potential of mean force along the needle channel. In addition, the potential energy itself generally has large fluctuations and its profile is misleading without the entropy contribution of protein conformations. Therefore, assuming that the interaction between the pulled MxiH and the needle is the main determinant to the underlying energetics of MxiH transport, we calculated the mean interaction energy profile along the channel axis to explore the energetics of MxiH transport across the needle channel. As shown in Fig. 5, although there is a more or less flat potential surface inside the channel, an energy barrier exists for MxiH to enter the needle, which, in fact, resembles the interaction energy profile between a chloride ion and the channel (Fig. 2). It should be noted that the total net charge of MxiH is −4e based on the standard protonation state at pH 7. Although individual trajectories exhibit variations in the energy profiles (Fig. S7, A and B), the energy barrier is higher for the two-helix bundle (17 kcal/mol) than for the straight helix (10 kcal/mol) in 150 mM salt concentration (Fig. 5). As expected, the barrier increases up to ∼40 kcal/mol for both systems when the salt concentration is reduced to 50 mM (Fig. S7, C and D).

Figure 5.

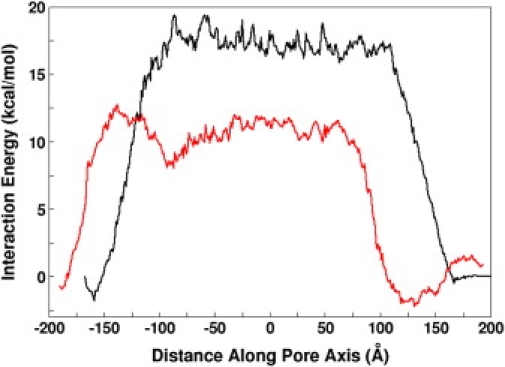
Mean interaction energy between the needle apparatus and the MxiH subunit along the channel axis: two-helix bundle (black) and straight helix (red).

We have examined the effects of pulling speed, MxiH orientation, and channel diameter on the energy barrier. First, we performed the pulling simulations with five-times lower pulling speed (3 Å/ns). Instead of repeating the simulations from the initial position, which would be very time consuming, 35 conformations at every 10 Å (from the bottom of the needle channel to the top) were taken from the pulling simulation trajectory with 15 Å/ns and simulated with 3 Å/ns to sample the conformational space at each region. The results clearly show that the energy barrier is not affected considerably (Fig. S8). Second, several other simulations that we have done with different starting conformations of MxiH monomer also reveal the presence of the electrostatic barrier, despite the marginal variation in the energy barrier. For instance, pulling of the straight helix with C-terminal facing the needle channel essentially yields the identical energy barrier as in the case of N-terminal facing the needle channel (Fig. S7 H). Third, as expected, the pulling simulations of straight helix (N-terminal facing the needle pore) and two-helix bundle across the needle channel of 30 Å inner diameter (3) yields smaller energy barriers, i.e., 7 kcal/mol (straight helix) and 12 kcal/mol (two-helix bundle), than those with the needle channel of 25 Å inner diameter (Fig. S7 and Fig. S9). Therefore, the presence of an energy barrier for MixH entrance into the needle is evident in all the cases.

Interestingly, examination of the surface electrostatics of structurally known TTSA components and effectors reveals similar excessive electronegative features. The channels in the basal body (EscJ and EscC) (4,5,31) are highly electronegative (Fig. 6, A–D), similar to the needle interior. EscN, the ATPase of E. coli, which is suggested to be anchored at the entrance of TTSA and acts as the inner-membrane recognition gate for chaperone-effector complexes (32), also possesses a highly electronegative channel interior (Fig. 6, E and F). Although no structure is available for the pore formed by the tip proteins that sit on the top of the needle channel, the monomeric tip proteins also contain excessive electronegative potential patches on their surfaces (Table S1 in the Supporting Material): IpaD from S. flexneri (PDB:2J0O) (9), LcrV from Y. pestis (PDB:1R6F) (10), and BipD from B. pseudomallei (PDB:2J9T) (9). Similar electronegative features are also seen in almost all effectors that are known to pass through the TTSA (Table S1). Therefore, our results suggest that the repulsive electrostatic interaction plays a key role in the export of the effectors through the TTSA.

Figure 6.

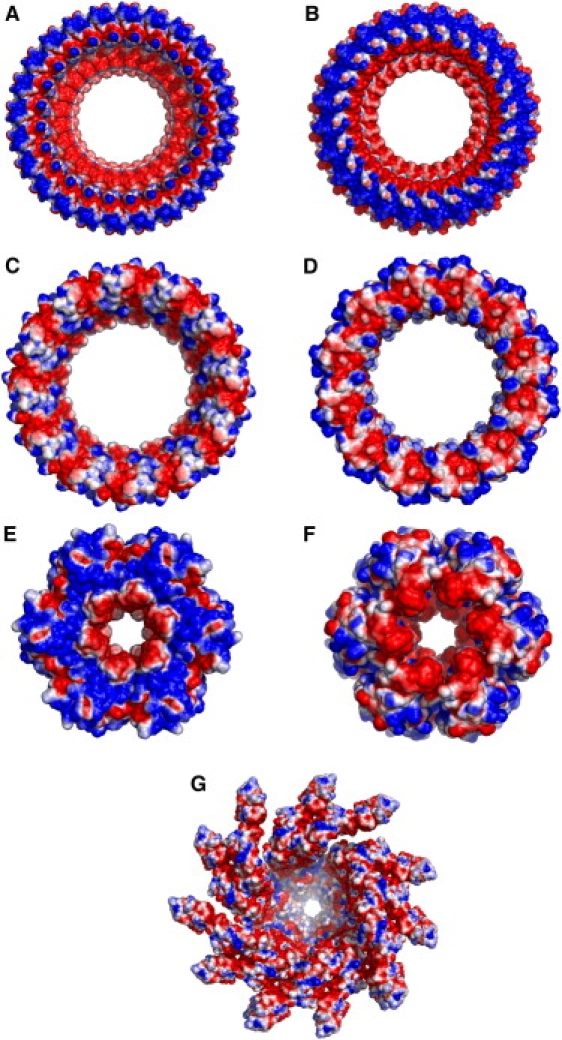
Surface electrostatics of the (A and B) EscJ, (C and D) EscC, (E and F) EscN, and (G) flagellar filament. Note that the visual scaling is different between of them. The electrostatic potentials are calculated by the PBEQ module (19) in CHARMM and visualized on the solvent-accessible surface using PyMOL (41). Electrostatic scaling used for all the figures is −0.6 (red) to 0.6 kcal/(mol·e) (blue).

Repulsive electrostatic mechanism of protein export through TTSA

Based on the energetics of MxiH export through the needle (Fig. 5) and the electronegative nature of the TTSA components (Fig. 6) and various effectors (Table S1), we propose a repulsive electrostatic mechanism for protein transportation through the TTSA channel. The excessive electronegative potential of the TTSA creates an potential gradient outside the TTSA and thus develops a repulsive energy barrier for the electronegative effectors to enter into the TTSA. However, there will be no (significant) energy barrier as soon as the effector proteins enter inside the TTSA, as shown in the case of MxiH. This implies that inside the TTSA, effector proteins may export through concentration-dependent passive diffusion, although one cannot rule out an electrostatic gradient inside the TTSA channel. We also expect that the unknown structures of other TTSA components facing the TTSA channel interior have the electronegative potential in line with the needle and the basal body. Our results suggest that this secretion system has evolved to have such repulsive interactions because any strong attractive interactions could cause trapping of proteins inside the TTSA channel, leading to that channel's obstruction.

The proposed mechanism raises an intriguing question about how effectors can enter the channel despite the presence of an electrorepulsive barrier at the entrance of the basal body. Based on this mechanism, the ATPase activity at the bottom of the TTSA and/or proton motive force (33) could be used to energize the protein translocation through these nanomachines. Thus, one can envision that the directionality of the effectors through the TTSA is regulated by the ATPase. However, the presence of specific intracellular chaperones for almost all the effectors as well as some of effector-chaperone complex structures clearly indicates that the directionality of the effectors toward the ATPase is regulated by those chaperones (3,34). A similar electronegative potential gradient at the exit of the TTSA channel may facilitate the effective ejection of the effectors into the host cell because, as seen in the case of MxiH, the energetics for effectors to be outside the channel is much favored over those inside.

As bacterial flagellar secretion apparatus shares many commonalties with the TTSA (3), we further investigated whether the electrorepulsive mechanism can be applicable to the assembly of the flagellar filament. Interestingly, the calculated electrostatic surfaces of the known structures of flagellar hook (35) (PDB:1UCU) and the filament monomer (36) (PDB:1WLG) as well as flagellar filament (Fig. 6 G) have electronegative features as seen in the TTSA components (Fig. 2 C and Fig. 6, A–F, and Table S1). In addition, other flagellar components show considerable electronegative patches (Table S2). Thus, these observations offer a clue that the flagellum may also export substrates using the proposed repulsive electrostatic mechanism. Although it is still under debate whether the proton motive force itself is enough for energizing the export (37) or whether ATPase is also necessary (38,39), it is well understood that the export process of the flagellum requires energy. Thus, the electrostatic potential gradient may play a role in the exportation process as evidenced by the results presented here.

Concluding Discussion

We have explored the mechanism of effector translocation through the TTSA channel by performing SMD simulations to export the MxiH monomer, the needle protein of S. flexneri (6), through its needle (Fig. 1). Because the system was too large for all-atom pulling simulations, we increased computational efficiency by using the GSBP formalism (16) to describe the mean solvent-mediated potential from the rigid needle model, and the GBSW (17) to describe the solvation of the flexible pulled MxiH monomer (see Appendix). Such combination of the implicit solvent models may provide a computational approach to other supramolecular complex systems that are still intractable for all-atom simulations. The needle channel modeling and MxiH pulling simulations revealed several intriguing results for the protein translocation mechanism through the TTSA.

We have independently modeled the needle based on published parameters because 1) the all-atom structure of the needle model by Deane et al. (6) was not available; and 2) a change in the dihedral angle of the hinge between the well-defined HTH and the modeled N-terminal α-helix would change the orientation of the residues facing the channel interior. The precise structure of the N-terminal region is not known, although it will not change the excessive electronegative potential inside the needle channel. Due to this uncertainty, our model and the model of Deane et al. (6) show differences in residues facing the channel interior. For example, the single tryptophan residue of MxiH (W10) is involved in monomer-monomer interactions in Deane's model, but it is facing the channel interior and forms the tryptophan groove in our model (Fig. 3 A). Our in vivo and in vitro experiments suggest that Trp¹⁰ may not be involved in the direct protein-protein interaction, but in protein transport through the needle instead, supporting our model. For example, we observed considerable differences in bacterial invasiveness in our W10 experimental mutation studies (W10Y, W10F, W10A, W10K, W10H, and W10R) (Table 1). It should be noted that all these mutant monomers can be expressed at levels equal to the wild-type and spontaneously polymerize into needles in vitro upon the removal of urea. This indicates that W10 is not involved in needle packing. In contrast, in vivo, the W10 mutations disrupt the needle formation, resulting in a shorter needle size that hampers the invasiveness of the bacteria: W10Y (134%) > W10 (100%) > W10F (34%) > W10A (no invasiveness) ≈ W10H (no invasiveness) ≈ W10R (no invasiveness) ≈ W10K (no invasiveness).

These results clearly indicate the importance of the tryptophan (aromatic) groove in the MxiH export for the needle formation in vivo. Interestingly, bacterial needle proteins have conserved Trp or Phe residue at the N-terminus (7).

The energetics deduced from the SMD trajectories based on the interaction between the pulled MxiH and the needle indicates that, whereas the potential surface is quite flat for MxiH transport inside the channel, there is an energy barrier for MxiH to enter the needle (Fig. 5), which is similar to the transportation of a chloride ion through the channel with a highly electronegative interior (Fig. 2, A and B). This energetic feature does not depend on the pulling speed, the orientation of pulled MixH, and the diameter of the channel interior. Detailed analyses of structurally known TTSA components and effectors also reveal excessive electronegative potential patches on their surfaces (Fig. 2 C and Fig. 6, A–F and Table S1). Based on these observations, we propose a repulsive electrostatic mechanism for the protein translocation through the TTSA. In this mechanism, the initial force required to surmount the energy barrier for proteins to enter into the TTSA may be offered by the ATPase as suggested experimentally (3). A similar electronegative potential gradient at the exit of the channel may facilitate the effective ejection of the effectors into the host cell and thus, the electrorepulsive mechanism may control the protein translocation across the TTSA. Based on the proposed mechanism, we speculate that the unknown structures of other TTSA components facing the TTSA channel interior may have similar electronegative potential. Interestingly, the bacterial flagellar secretion apparatus that shares many common features with the TTSA also has an electronegative channel, suggesting that the flagellar apparatus may also use a similar repulsive electrostatic mechanism for substrate transportation (Fig. 6 G and Table S2). These secretion systems appear to have evolved this repulsive mechanism because any strong attractive interactions could cause trapping of proteins inside the channel, leading to obstruction of the protein channel. We expect that a similar mechanism may be applicable to macromolecular channels in other secretion systems or viruses through which proteins or nucleic acids are transported, e.g., protein channels that act as conduits during the DNA packing inside various virus capsids.

Another interesting result is the screwlike rotation involved in the export of the two-helix bundle across the needle channel (Fig. 3 B and Movie S1). The attempt to relate such motions to the tryptophan groove inside the needle channel (Fig. 3 A) has been made by additional pulling simulations of the W10 mutants. However, similar screwlike motions were observed even in the pulling simulations of W10A, W10F, and W10Y mutants (Fig. 3 and Fig. S2), indicating that such rotation appears to be the characteristic feature of the export of two-helix bundles, and which may be dictated by the tight packing of the needle. The mutation effects on the transport energetics are also minor (Fig. S7, E–G). Clearly, the present pulling simulations with the needle model cannot quantitatively explain the differences in bacterial invasiveness of the mutants. This might be due to 1) the use of implicit solvent models with the rigid needle, which were sufficient to investigate the macroscopic energetics of the MxiH export process, but not detailed enough to capture the specific interaction between the needle and MxiH; and 2) the accuracy of the current needle model. Although we need to refine the needle model based on more experimental information, the tryptophan groove in our needle model and the W10 experimental mutation studies suggest the possibility of having energetically favorable stacking interactions between W10s of the tryptophan groove and W10 of exporting MxiH. The role of such stacking interaction guided by the greasy slide made of the aromatic residues (W, Y, and F) is also observed in maltoporin, which is responsible for the sugar transport in Gram-negative bacteria (26,27). Further, it has also been shown that the mutation of W/F to A at the entrance/exit of the channel reduced the sugar uptake considerably (28).

Finally, it is still unknown whether MxiH translocates through the needle as a two-helix bundle, as an extended helix, or in a completely disordered conformation. However, our simulation shows the possibility of the MxiH subunit to be exported across the needle apparatus in the two-helix bundle form. Our results indicate that the N- and C-terminal regions tend to lose the α-helical conformation and adopt a partially folded conformation during the export process. Interestingly, this is in accordance with the earlier prediction that the effectors would have to be in a partially or totally unfolded form to be exported across the TTSA (40).

Appendix

Let us consider that A and B represent a rigid needle apparatus and a flexible (pulled) MxiH monomer, respectively. Then, the total effective energy of the system can be expressed as (16)

$$E=U^{\text{AA}}+U^{\text{BB}}+U^{\text{AB}}+\Delta G_{\text{elec}}+\Delta G_{\text{np}}\text{.}$$ (A1)

U^AA and U^BB are the potential energy of A and B. U^AB is the interaction energy between A and B, which can be written as the sum of electrostatic ($U_{\text{elec}}^{\text{AB}}$) and van der Waals ($U_{\text{vdW}}^{\text{AB}}$) interactions, i.e., $U^{\text{AB}}=U_{\text{elec}}^{\text{AB}}+U_{\text{vdW}}^{\text{AB}}$. ΔG_elec and ΔG_np are the electrostatic and nonpolar solvation free energy terms. ΔG_elec is given by (16)

$$\Delta G_{\text{elec}}=\frac{1}{2}\int d\mathbf{r}d\mathbf{r}\prime {\rho }_{\text{A}}\left(\mathbf{r}\right){\text{G}}_{\text{rf}}\left(\mathbf{r},\mathbf{r}\prime \right){\rho }_{\text{A}}\left(\mathbf{r}\prime \right)+\int d\mathbf{r}d\mathbf{r}\prime {\rho }_{\text{A}}\left(\mathbf{r}\right){\text{G}}_{\text{rf}}\left(\mathbf{r},\mathbf{r}\prime \right){\rho }_{\text{B}}\left(\mathbf{r}\prime \right)+\frac{1}{2}\int d\mathbf{r}d\mathbf{r}\prime {\rho }_{\text{B}}\left(\mathbf{r}\right){\text{G}}_{\text{rf}}\left(\mathbf{r},\mathbf{r}\prime \right){\rho }_{\text{B}}\left(\mathbf{r}\prime \right)\text{.}$$ (A2)

G_rf (r,r′) is the reaction field potential at r due to a unit charge at r′. ρ_A(r) and ρ_B(r) are charge distributions in A and B, respectively. The first term is the electrostatic solvation free energy of A, which is a constant and thus can be neglected because A is kept fixed during the simulation. The second term is the coupling between the charges in A and B. This can be represented as the difference between the electrostatic interactions in the solvent dielectric environment and in vacuum, i.e.,

$$\int d\mathbf{r}{\rho }_{\text{B}}\left(\mathbf{r}\right)\left({\varphi }_{\varepsilon =80}^{\text{A}}\left(\mathbf{r}\right)-{\varphi }_{\varepsilon =1}^{\text{A}}\left(\mathbf{r}\right)\right),$$

where ${\varphi }_{\varepsilon =80}^{\text{A}}\left(\mathbf{r}\right)$ is the electrostatic potential from A in the solvent dielectric environment. Because $\int d\mathbf{r}{\rho }_{\text{B}}\left(\mathbf{r}\right){\varphi }_{\varepsilon =1}^{\text{A}}\left(\mathbf{r}\right)$ simply corresponds to the Coulombic interaction between A and B in vacuum ($U_{\text{elec}}^{\text{AB}}$),

$$\Delta G_{\text{elec}}+U_{\text{elec}}^{\text{AB}}=\int d\mathbf{r}{\rho }_{\text{B}}\left(\mathbf{r}\right){\varphi }_{\varepsilon =80}^{\text{A}}\left(\mathbf{r}\right)+\frac{1}{2}\int d\mathbf{r}d\mathbf{r}\prime {\rho }_{\text{B}}\left(\mathbf{r}\right){\text{G}}_{\text{rf}}\left(\mathbf{r},\mathbf{r}\prime \right){\rho }_{\text{B}}\left(\mathbf{r}\prime \right)\text{.}$$ (A3)

The static external potential ${\varphi }_{\varepsilon =80}^{\text{A}}\left(\mathbf{r}\right)$ can be calculated by solving the finite-difference PB equation (19). Because ${\varphi }_{\varepsilon =80}^{\text{A}}\left(\mathbf{r}\right)$ is independent of the instantaneous position of B, it is computed only once and used for the entire simulation (16). However, the second term depends on the instantaneous position of B and needs to be calculated every time-step during the simulation. Because solving the PB equations at every time-step is computationally very expensive, a generalized multipole approximation has been applied earlier (16). However, in this study, we used a generalized Born model (ΔG_GB^B) to approximate the second term in Eq. A3, assuming that the reaction field arising from the dielectric boundary of A is negligible.

The nonpolar solvation energy ΔG_np in Eq. A1 includes the formation of a cavity in the solvent as well as solvent-solute van der Waals interactions (20,21). In addition, the van der Waals interaction between A and B ($U_{\text{vdW}}^{\text{AB}}$) includes the attractive ($U_{\text{attractive}}^{\text{AB}}$) and repulsive ($U_{\text{repulsive}}^{\text{AB}}$) components. Because A is fixed, when B approaches to A, ΔG_np will decrease and $U_{\text{attractive}}^{\text{AB}}$ will increase. For the sake of simplicity and computational efficiency, we assume that ΔG_np and $U_{\text{attractive}}^{\text{AB}}$ cancel each other and $U_{\text{repulsive}}^{\text{AB}}$ can be represented by a grid-based repulsive core potential U_core, i.e.,

$$\Delta G_{\text{np}}+U_{\text{vdW}}^{\text{AB}}\approx U_{\text{core}}\text{.}$$ (A4)

In terms of Eqs. A3 and A4, the total effective energy in Eq. A1 becomes

$$E=U^{\text{BB}}+\Delta G_{\text{GB}}^{\text{B}}+\sum _{\alpha \in \text{B}}{q}_{\alpha }{\varphi }_{\varepsilon =80}^{\text{A}}\left({\mathbf{r}}_{\alpha }\right)+\sum _{\alpha \in \text{B}}{U}_{\text{core}}\left({\mathbf{r}}_{\alpha }\right),$$ (A5)

where q_α is the charge of atom α in B. We used the GBSW (17) in CHARMM for ΔG^B_GB.

Based on Eq. A5, the needle apparatus has been treated implicitly during the pulling simulation through the static field electrostatic potential (${\varphi }_{\varepsilon =80}^{\text{A}}$) arising from the needle protein charges and the grid-based core repulsive potential (U_core) arising from the shape of the needle channel. ${\varphi }_{\varepsilon =80}^{\text{A}}$ was calculated with a dielectric constant of 2 for the protein interior and 80 for the bulk solvent region with 150 mM salt concentration using the PBEQ module (20,22) in CHARMM. The optimized PB atomic radii have been used to set up the dielectric boundary (20). The electrostatic potential was first calculated with a coarse grid (63 × 63 × 187 with a grid-spacing of 2.0 Å) centered on the entire needle apparatus. The result of the coarse calculation was then used to set the potential on the edge of a smaller box to perform second and third calculations using finer grids (95 × 95 × 355 with a grid-spacing of 1.0 Å for the second and 71 × 71 × 701 with a grid-spacing of 0.5 Å for the third) centered on the needle apparatus. The PB radii augmented by the hydration radii were used to set up the molecular surface (22) by which a core repulsion potential map was built and stored on a grid (71 × 71 × 701 with a grid-spacing of 0.5 Å). It was set to be zero in an all-accessible region and 50 kcal/mol otherwise. The core repulsive energy and forces were calculated using the third-order B-spline interpolation (23,24).

Although the method described above can be efficiently used to increase the computational speed, it does have a limitation. For instance, the lack of explicit interactions between the needle channel and MxiH ($U_{\text{elec}}^{\text{AB}}$ and $U_{\text{vdW}}^{\text{AB}}$) in the total energy may have influence in capturing the specific interaction between them. However, such a limitation is unlikely to change the general conclusion of this study.

Supporting Material

Nine figures, two tables, and two movies are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01672-5.