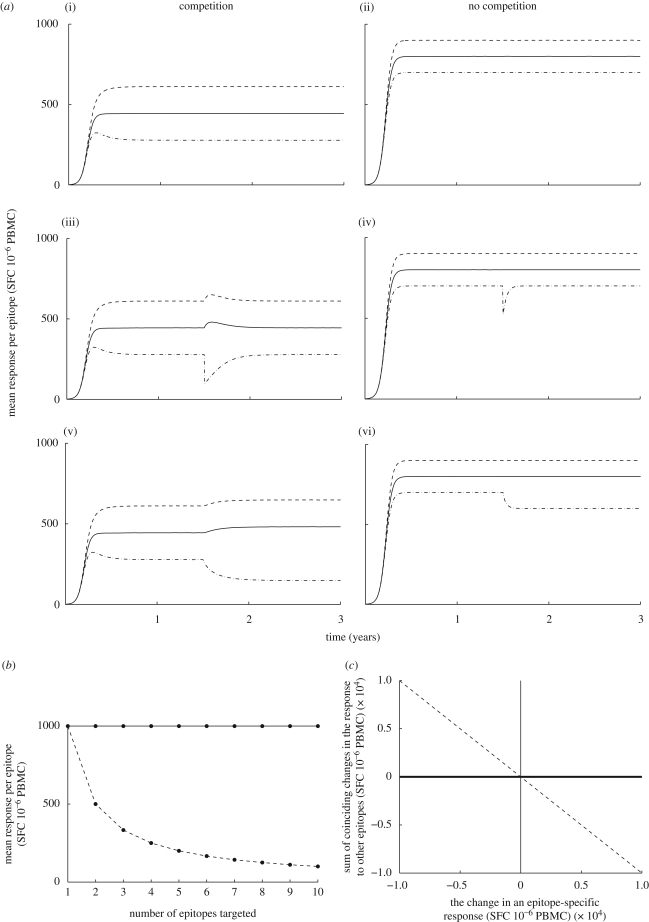
Figure 1.
Model predictions. (a) Predicted behaviour under the Lotka–Volterra model in the presence and absence of competition between HIV-specifc CTL specificities. In (i), (iii) and (v), there is competition between CTLs specific for different epitopes, whereas in (ii), (iv) and (vi), there is no competition (αij = 0 for all i and all j, i ≠ j). In (i) and (ii) there is no change in CTL specific for either of three epitopes. In (iii) and (iv) there is a sporadic decrease in CTL specific for one of three epitopes (epitope 3). In (v) and (vi) there is a decrease in the carrying capacity of CTL specific for epitope 3. The figures show that if a decrease (or increase) occurs in the response to one epitope, then other responses will increase (or decrease) if there is competition between specificities. Changes in other responses will be temporary following a sporadic change in the response to one epitope, but permanent following a change in the carrying capacity of one epitope. The following model parameters were used: K1 = 900, K2 = 800 and K3 = 700; ri = 30 for all i and αij = 0.4 for all i and all j when there is competition. The starting values were Ni(0) = 0 for all i. In (iii) and (iv), the response to epitope 3 decreases by 200 at time t = 1.5 years. In (v) and (vi), the carrying capacity for CTLs directed against epitope 3 decreases to 600 at t = 1.5 years. Dashed lines, epitope 1; solid lines, epitope 2; dashed-dotted lines, epitope 3. (b) Model prediction of how the mean response per epitope varies with the number of epitopes targeted. If there is no interspecific competition (solid line), the mean response does not vary with the number of epitopes targeted, whereas if there is interspecific competition (dashed line) (αij > 0 for some i and j), the mean response per epitope decreases with the number of epitopes targeted. For this example, we have assumed that the carrying capacity, Ki, of each epitope-specific response is the same (Ki = 1000) and that interspecific competition between each specificity is as strong as intraspecific competition (αij = 1 for all i and j). In this particular case, the mean response is inversely proportional to the number of epitopes targeted. (c) Model prediction of how the change in the response directed against a single epitope would correspond to the change in the sum of the responses directed against other epitopes. If there is no interspecific competition, significant changes in the response directed against one epitope would not correspond to changes in the total response directed against other epitopes (solid line). If there is interspecific competition, an increase in the response directed against one epitope would correspond to a decrease in the total response directed against other epitopes (dashed line). These changes would be exactly equal in magnitude (as shown) if interspecific competition is as strong as intraspecific competition.