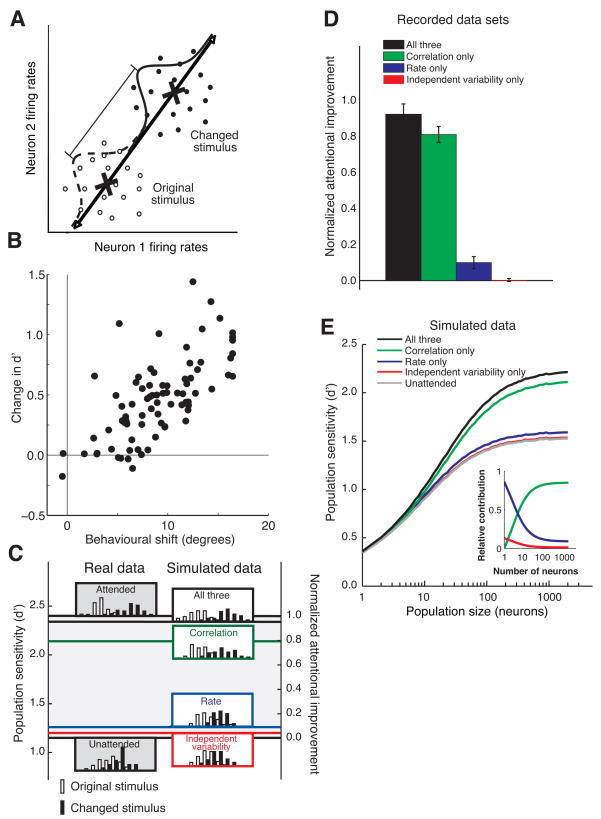
Figure 4.

Modulation of noise correlation accounts for the majority of the attentional improvement in population sensitivity. A. Procedure for calculating the sensitivity of the population. For each trial and attentional condition, the firing rate response of the n neurons recorded simultaneously in a given hemisphere to the stimulus immediately before the orientation change (open circles) and the changed stimulus (filled circles) is plotted as a point in an n-dimensional space (a fictional two-neuron example is plotted here). The axis of discrimination (black line) is the line connecting center of mass of the n-dimensional cloud of points for each time period (X’s). Each point is projected onto the axis, leaving a one-dimensional distribution of projected values for each time period (dashed and solid curves). The sensitivity of the population to the change in the stimulus is quantified as the discriminability of the two distributions in units of d′ (the difference between changed mean and original mean divided by the standard deviation). B. Population d′ and behavioral improvement are highly correlated. For each hemisphere-day, population d′ is plotted as a function of the behavioral improvement (quantified as the lateral shift between performance at the unattended location and the fitted psychometric curve for the attended condition). C. Procedure for calculating the amount of the observed attentional improvement explained by each factor for a representative example data set. Histograms of projections onto the axis defined in A are plotted for the real data (left column, for attended and unattended trials), and for simulations (right column). We defined the observed attentional improvement as the difference between the d’s for the two attentional conditions (d′=2.40 for the attended condition and 1.15 for the unattended condition, giving an improvement of 1.25 in this example). The left axis represents d′ and the right axis represents normalized proportion of attentional improvement (by definition 1.0 for the attended condition and 0.0 for the unattended condition). To isolate the contribution of each factor (or group of factors), we simulated responses of an identically sized population of neurons with the same mean firing rate, Fano factor, and noise correlation as each of the neurons in our data set in which the statistics of the labeled factor/s matched the data for the attended condition and the other factors matched the data for the unattended condition (right column of distributions). We calculated the fraction of the observed attentional improvement explained by each factor/s by comparing the simulated d′ to the d′ for the real unattended data. In this data set, modulation of independent variability (at the level predicted if changes in Fano factor were due solely to changes in independent variability) accounted for 4% of the observed attentional improvement, rate accounted for 9%, correlation accounted for 79%, and the three together accounted for 95%. D. Average proportion of actual attentional improvement for all 82 data sets. Each day of data contributed two data sets (one for each hemisphere). Error bars represent SEM. All proportions are statistically different from zero (t-test, p<0.01) except the independent variability-only simulation (p=0.82). E. Population sensitivity as a function of the number of neurons involved in the task. Population d′ was calculated using the method described in A and B except that data in both the attended and the unattended conditions were simulated. For each population size, we sampled, with replacement, from the entire population of neurons from all data sets combined. Each simulation was run 100 times for 10,000 trials on each run. The inset plots the relative contribution of each factor (which is the ratio of the improvement in d′ for that factor alone to the improvement in d′ for all three factors) as a function of population size. Correlation is the most important factor for population sizes greater than 5 (crossing of the green and blue lines).