Comparison of Isotonic Designs for Dose-Finding

Abstract

We compare several decision rules for allocating subjects to dosages that are based on sequential isotonic estimates of a monotone dose–toxicity curve. We conclude that the decision rule in which the next assignment is to the dose having probability of toxicity closest to target does not work well. The best rule in our comparison is given by the cumulative cohort design. According to this design, the dose for the next subject is decreased, increased, or repeated depending on the distance between the estimated toxicity rate at the current dose and the target quantile.

1. Introduction

Consider a dose-finding trial with the goal of finding a dose with certain target toxicity rate Γ, the maximum tolerated dose (MTD). That is, the goal is to find a dose where approximately Γ*100% of subjects have toxicity. In phase I studies in oncology, Γ is usually set to 0.2 or 0.25. The value of Γ can be as small as 0.05 or 0.1 for acute toxicity studies relevant to endangered species. In acute toxicity studies designed to determine labeling requirements for consumer products, the value of Γ is usually set to 0.5. Dose-finding designs are often classified as nonparametric and parametric. Biased coin designs (Durham and Flournoy 1994), group up-and-down designs (Wetherill 1963), escalation and A + B designs (Lin and Shih 2001) are referred to as nonparametric designs. An advantage of these procedures is that they have easy-to-implement decision rules. Ivanova (2006) reviewed some nonparametric designs and their rules of construction for a given target toxicity rate Γ. Parametric designs typically assume a model for dose–toxicity relationship in which one or two parameters require estimation. The most widely studied parametric design is the continual reassessment method (O’Quigley, Pepe, and Fisher 1990).

Decision rules in many nonparametric designs have implicitly used, but not taken full advantage of, an assumption that toxicity is an increasing function of dose because decision rules in these designs have been based on the outcomes of last cohort of subjects only. Taking full advantage (nonparametrically) of the monotonicity assumption requires fitting an isotonic regression model to all the data. A few designs in which the decision rules are formulated as functions of isotonic estimates of the toxicity probabilities have appeared recently. Leung and Wang (2001) proposed an isotonic design for trials with one drug. Conaway, Dunbar, and Peddada (2004) and Ivanova and Wang (2004) suggested designs for trials with two drugs. Yuan and Chappell (2004) and Ivanova and Wang (2006) proposed isotonic designs for trials with ordered groups. The common feature in all these designs is that the probability of toxicity at each step is estimated using isotonic regression. However, the authors suggested different rules for how to use the estimates to decide what dose to choose for the next assignment. Though methods for two treatments and ordered groups employ bivariate or partial order isotonic estimators, the decision rules are essentially one-dimensional. In this article, we compare the one-dimensional decision rules to use in isotonic-based designs and recommend the best rule. The decision rules are described in Section 2. In Section 3, we compare the designs via simulations. The results are discussed in Section 4.

2. Isotonic Designs to Find the MTD

Let D = {d₁, …, d_K} denote the set of ordered dose levels. Let F(d) be the probability of toxicity at dose d and let q_j = F(d_j), j = 1, …, K. Assume that F(d) is a nondecreasing function of d. The maximum tolerated dose is defined as the dose with the probability of toxicity equal to a fixed target value Γ. Consider the goal of finding a dose in D having probability of toxicity closest to Γ.

First we describe how to obtain isotonic estimates of toxicity probabilities. When the dose–response experiment involves a simple ordering, that is, q₁ ≤ · · · ≤ q_K, isotonic estimates may be found using the pool-adjacent-violators algorithm (see Robertson, Wright, and Dykstra 1988). Let ${\widehat{\widehat{q}}}_j$ denote the observed proportion of n_j subjects with toxicity at dose d_j and let q̂_j denote the corresponding isotonic estimate of the probability of toxicity, for j = 1, …, K. If the { ${\widehat{\widehat{q}}}_j$} are ordered, that is, ${\widehat{\widehat{q}}}_1\le \cdots \le {\widehat{\widehat{q}}}_K$, then the ${\widehat{q}}_j={\widehat{\widehat{q}}}_j$, j = 1, …, K, are the isotonic estimates. Otherwise, consider each ${\widehat{\widehat{q}}}_j$. When you find a dose d_j, such that ${\widehat{\widehat{q}}}_j>{\widehat{\widehat{q}}}_{j+1}$, the isotonic estimates are the weighted average ${\widehat{q}}_j={\widehat{q}}_{j+1}=(n_j{\widehat{\widehat{q}}}_j+n_{j+1}{\widehat{\widehat{q}}}_{j+1})/(n_j+n_{j+1})$, where the weights are the current sample sizes at the two doses. For calculation purposes, replace these two estimates with one denoted by q̂_j+ for “dose” d_j+ with weight n_j+ = n_j + n_j+1. Look again for a dose d_j for which the working isotonic estimate is greater than the working estimate at the next higher “dose”, and repeat the averaging and concatenation process until isotonicity is actually obtained, that is, until q̂₁ ≤ · · · ≤ q̂_K. We note that the isotonic estimates are equivalent to the maximum likelihood estimates assuming only that q₁ ≤ · · · ≤ q̂_K. Roberson, Wright, and Dykstra (1988) gave other computational algorithms.

In the designs we consider, subjects can be treated in cohorts of size s or one at a time (s = 1). The isotonic estimates of toxicity rates {q̂_j} are updated after the responses of each cohort are obtained. Suppose that the current cohort of subjects was treated at d_j and that the isotonic estimates {q̂_j} of the toxicity probabilities have been updated. The three decision rules we will compare are described in the following.

2.1 Isotonic Design by Leung and Wang (2001)

This decision rule uses the estimated toxicity rate at d_j, as well as those at the adjacent doses: d_j−1 and d_j+1. The next dose according to the algorithm below is one of {d_j−1, d_j, d_j+1} with the probability of toxicity closest to Γ.

1. If q̂_j < Γ and Γ − q̂_j ≥ q̂_j+1 − Γ, treat the next cohort at $\{\begin{array}{cc}{d}_{j+1},& 1\le j<K\\ d_j,& j=K\end{array}$;

2. if q̂_j ≥ Γ and Γ − q̂_j−1 < q̂_j − Γ, treat the next cohort at $\{\begin{array}{cc}{d}_{j-1},& 1<j\le K\\ d_j,& j=1\end{array}$;

3. otherwise, treat the next cohort at d_j.

2.2 The “Closest Dose” Decision Rule From Conaway et al. (2004)

This decision rule uses estimated toxicity rates at all doses. The “closest dose” decision rule is based on the natural desire to select the next dose with estimated toxicity rate as close to the MTD as possible. Such a decision rule works well with parametric designs, for example, the continual reassessment method (CRM; O’Quigley et al. 1990). Conaway et al. (2004) suggested the “closest dose” decision rule for their two-dimensional design that used partial ordering isotonic estimates. Converted to one-dimensional simple order problem their decision rule with symmetric loss is defined as follows:

1. Determine the “suggested” dose level. For that, first identify dose levels with estimated toxicity rate closest to Γ, that is, where |q̂_i − Γ| is minimized. If there is one such dose, it is the “suggested” dose level. If there are two or more such doses, the lowest of the doses is chosen, except when all doses have estimated toxicity rate lower than Γ, in which case the highest of the doses is chosen. Let the “suggested” dose level be d_i with the estimated toxicity level q̂_i.

2. If q̂_i < Γ, 1 ≤ i < K, and higher doses have not been tried yet, the next cohort is treated at d_i+1, otherwise treat the next cohort at the dose level d_i.

2.3 Cumulative Cohort Design from Ivanova, Flournoy, and Chung (2007)

In this design, the decision rule depends on the estimated toxicity rate at the current dose only. The dose is not changed if the toxicity rate at the current dose is close to the target (within Δ > 0 of the target), and it is changed otherwise. The decision rule for the cumulative cohort design is

1. If q̂_j ≤ Γ − Δ, treat the next cohort at $\{\begin{array}{cc}{d}_{j+1},& 1\le j<K\\ d_j,& j=K\end{array}$;

2. if q̂_j ≥ Γ + Δ, treat the next cohort at $\{\begin{array}{cc}{d}_{j-1},& 1<j\le K\\ d_j,& j=1\end{array}$;

3. if Γ − Δ < q̂_j < Γ + Δ, treat the next cohort at d_j.

Ivanova et al. (2007) obtained the cumulative cohort design as a generalization of group up-and-down designs. They suggested choosing the parameter Δ to maximize the number of subjects assigned to the MTD in trials with moderate sample sizes. Based on this criterion they recommended using Δ = 0.09 if Γ = 0.10, 0.15, 0.20 or 0.25; Δ = 0.10 if Γ = 0.30 or 0.35; Δ = 0.12 if Γ = 0.40; and Δ = 0.13 if Γ = 0.45 or 0.50. Another natural choice of parameter Δ in the cumulative cohort design is Δ close to 0. For example, with Δ = 0.01 for moderate sample sizes, the dose is repeated if the estimated toxicity rate is exactly equal to Γ, and changed otherwise. In Section 3 herein, we simulated the cumulative cohort design that uses the “optimal” parameter Δ and the cumulative cohort design with Δ = 0.01.

Yuan and Chappell (2004), among other rules to target Γ = 0.2, suggested an ad hoc decision rule: the dose was not changed if the estimated toxicity rate was within Γ ≤ q̂_j < 2Γ. This rule is in the spirit of cumulative cohort design but with asymmetric window around the target. To use this rule with variety of targets Γ, we modified it as follows: the dose is not changed if the estimated toxicity rate is within Γ ≤ q̂ _j < Γ + 2Δ and changed otherwise, where Δ is the “optimal” parameter from Ivanova et al. (2007). That is, for Γ = 0.10 and Γ = 0.25, the dose is not changed if Γ ≤ q̂ _j < Γ + 0.18; for Γ = 0.50, the dose is not changed if Γ ≤ q̂ _j < Γ + 0.26. We refer to this rule as Yuan and Chappell’s rule.

3. Comparing Designs

We compared designs for Γ = 0.10, 0.25, and 0.50 using four dose–toxicity scenarios that are given in Table 1. Comparisons were obtained by simulating each design 4,000 times for each dose–toxicity scenario. After a startup procedure has completed (described below), each simulation evolves in cohorts of size one. The results are given in Tables 2–4 and Figures 1 and 2. The cumulative cohort design was simulated with the “optimal” parameter Δ (Ivanova et al. 2007) as well as with the parameter Δ = 0.01. Our goal was to compare the underlying decision rules so we fixed the sample size and did not employ stopping rules. At the end of the trial the MTD was estimated using the isotonic estimates of toxicity rates at all doses. If there were two or more doses with estimates closest to Γ, the lowest of the doses was chosen except for the case where all such doses have estimated toxicity rate lower than Γ, in which case the highest of these doses was chosen.

Table 1.

Four toxicity scenarios

	d1	d2	d3	d4	d5	d6
Scenario 1: F(dj)	0.12	0.25	0.50	0.60	0.75	0.85
Scenario 2: F(dj)	0.01	0.10	0.25	0.50	0.64	0.76
Scenario 3: F(dj)	0.00	0.10	0.18	0.25	0.50	0.63
Scenario 4: F(dj)	0.00	0.01	0.05	0.10	0.25	0.40

Table 2.

Percent recommendation of each dose as the MTD, the average number of subjects allocated to each dose, and the average number of toxicities in the trial for the cumulative cohort decision rule with optimal Δ = 0.09 (CCD), the cumulative cohort decision rule with Δ = 0.01 (CCD 0), Yuan and Chappell’s decision rule (YC), Leung and Wang’s decision rule (LW), and “closest dose” decision rule (CD). The total sample size is 30. Results at the MTD are in bold. The target is Γ = 0.1

	Percent recommendation						Allocation
	d1	d2	d3	d4	d5	d6	d1	d2	d3	d4	d5	d6	Toxicities
Scenario 1
CCD	0.88	0.12	0.00	0.00	0.00	0.00	21.3	7.2	1.3	0.1	0.0	0.0	5.1
CCD 0	0.85	0.14	0.01	0.00	0.00	0.00	19.3	8.2	2.1	0.3	0.1	0.0	5.6
YC	0.78	0.21	0.01	0.00	0.00	0.00	16.1	11.0	2.5	0.3	0.1	0.0	6.2
LW	0.92	0.08	0.00	0.00	0.00	0.00	23.5	5.2	1.1	0.2	0.0	0.0	4.8
CD	0.93	0.07	0.00	0.00	0.00	0.00	23.9	4.8	1.1	0.2	0.0	0.0	4.7
Scenario 2
CCD	0.19	0.67	0.13	0.00	0.00	0.00	7.5	14.2	7.0	1.3	0.1	0.0	3.9
CCD 0	0.19	0.60	0.19	0.02	0.00	0.00	8.6	12.1	7.3	1.8	0.2	0.0	4.2
YC	0.09	0.65	0.24	0.02	0.00	0.00	5.3	12.1	9.8	2.4	0.3	0.1	5.2
LW	0.43	0.49	0.08	0.00	0.00	0.00	12.6	12.0	4.4	0.9	0.1	0.0	2.9
CD	0.48	0.46	0.06	0.00	0.00	0.00	13.4	11.6	4.1	0.9	0.1	0.0	2.8
Scenario 3
CCD	0.14	0.55	0.23	0.08	0.00	0.00	6.2	13.4	7.1	2.6	0.6	0.0	3.6
CCD 0	0.14	0.45	0.26	0.12	0.02	0.00	7.9	11.2	7.0	2.8	0.9	0.1	3.6
YC	0.07	0.40	0.34	0.17	0.02	0.00	4.9	10.6	8.4	4.3	1.4	0.3	4.5
LW	0.41	0.39	0.16	0.04	0.00	0.00	12.4	10.5	5.0	1.8	0.4	0.0	2.6
CD	0.45	0.37	0.15	0.04	0.00	0.00	12.9	10.2	4.8	1.8	0.4	0.0	2.5
Scenario 4
CCD	0.00	0.07	0.29	0.49	0.15	0.01	4.1	5.5	7.9	7.4	4.1	1.0	2.6
CCD 0	0.00	0.03	0.22	0.46	0.26	0.03	4.3	5.9	7.6	6.9	4.1	1.2	2.6
YC	0.00	0.01	0.17	0.53	0.27	0.03	4.1	4.6	6.3	7.5	5.5	2.0	3.2
LW	0.04	0.19	0.31	0.37	0.09	0.01	5.0	7.3	7.8	6.5	2.7	0.7	2.1
CD	0.04	0.21	0.31	0.35	0.08	0.00	4.9	7.6	7.7	6.3	2.7	0.7	2.0

Table 4.

Percent recommendation of each dose as the MTD, the average number of subjects allocated to each dose, and the average number of toxicities in the trial for the cumulative cohort decision rule with optimal Δ = 0.13 (CCD), the cumulative cohort decision rule with Δ = 0.01 (CCD 0), Yuan and Chappell’s decision rule (YC), Leung and Wang’s decision rule (LW), and “closest dose” decision rule (CD). The total sample size is 30. Results at the MTD are in bold. The target is Γ = 0.5.

	Percent recommendation						Allocation
	d1	d2	d3	d4	d5	d6	d1	d2	d3	d4	d5	d6	Toxicities
Scenario 1
CCD	0.00	0.10	0.61	0.26	0.03	0.00	2.1	6.7	12.8	6.5	1.7	0.3	13.7
CCD 0	0.00	0.09	0.58	0.28	0.04	0.00	2.2	7.3	10.9	6.7	2.4	0.4	13.7
YC	0.01	0.08	0.43	0.39	0.09	0.00	1.5	3.1	7.8	9.7	6.1	1.6	16.7
LW	0.06	0.23	0.40	0.22	0.09	0.01	2.9	7.4	10.5	6.1	2.6	0.5	13.5
CD	0.25	0.37	0.23	0.12	0.03	0.01	8.3	11.0	6.5	3.2	0.9	0.2	9.7
Scenario 2
CCD	0.00	0.00	0.11	0.66	0.22	0.02	1.2	1.9	6.6	13.1	5.8	1.4	13.2
CCD 0	0.00	0.00	0.11	0.65	0.22	0.02	1.2	2.1	7.4	11.2	6.3	1.8	13.2
YC	0.00	0.01	0.10	0.51	0.35	0.04	1.1	1.5	3.1	8.5	9.9	5.9	16.0
LW	0.00	0.05	0.24	0.42	0.22	0.07	1.1	2.5	7.3	10.9	6.0	2.2	13.0
CD	0.10	0.21	0.35	0.22	0.09	0.03	3.9	6.8	10.0	6.1	2.6	0.7	8.4
Scenario 3
CCD	0.00	0.00	0.00	0.13	0.63	0.24	1.1	1.6	2.5	6.3	11.8	6.6	12.2
CCD 0	0.00	0.00	0.00	0.12	0.66	0.22	1.1	1.6	2.5	7.1	10.8	6.9	12.2
YC	0.00	0.00	0.01	0.11	0.55	0.33	1.1	1.4	1.7	3.2	8.1	14.6	14.5
LW	0.00	0.03	0.10	0.24	0.37	0.26	1.1	2.2	3.7	7.0	9.2	6.8	11.5
CD	0.10	0.16	0.20	0.27	0.18	0.11	3.7	5.3	6.0	7.5	4.8	2.8	7.6
Scenario 4
CCD	0.00	0.00	0.00	0.00	0.06	0.94	1.0	1.1	1.3	1.9	4.8	19.9	9.4
CCD 0	0.00	0.00	0.00	0.00	0.05	0.95	1.0	1.1	1.3	2.1	5.5	19.0	9.3
YC	0.00	0.00	0.00	0.00	0.05	0.95	1.0	1.1	1.2	1.5	2.4	22.8	9.3
LW	0.00	0.00	0.01	0.06	0.18	0.74	1.0	1.1	1.5	2.7	5.7	18.1	9.0
CD	0.01	0.05	0.09	0.22	0.25	0.38	1.3	2.4	3.4	6.4	6.8	9.7	6.4

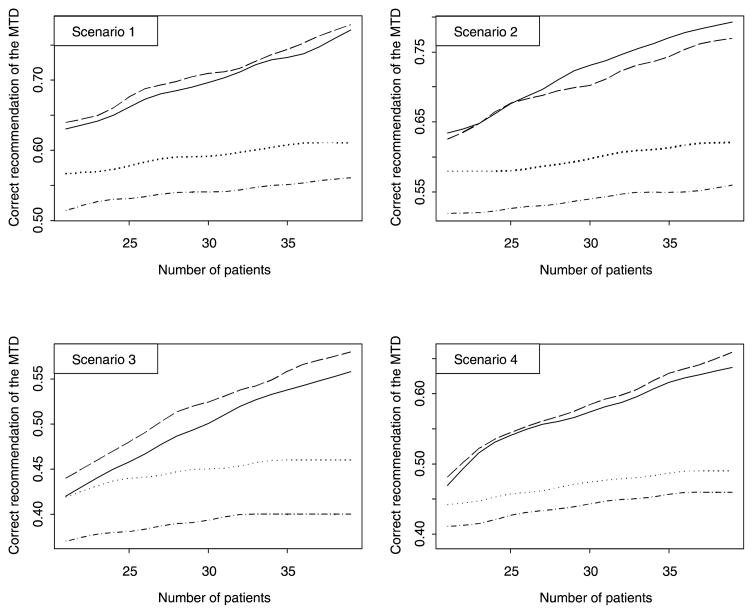
Figure 1.

Percent of correctly recommending the MTD for the cumulative cohort decision rule with optimal Δ (solid line), the cumulative cohort decision rule with Δ = 0.01 (dashed line), Leung and Wang’s decision rule (dotted line), and the closest dose decision rule (dotted-dashed line).

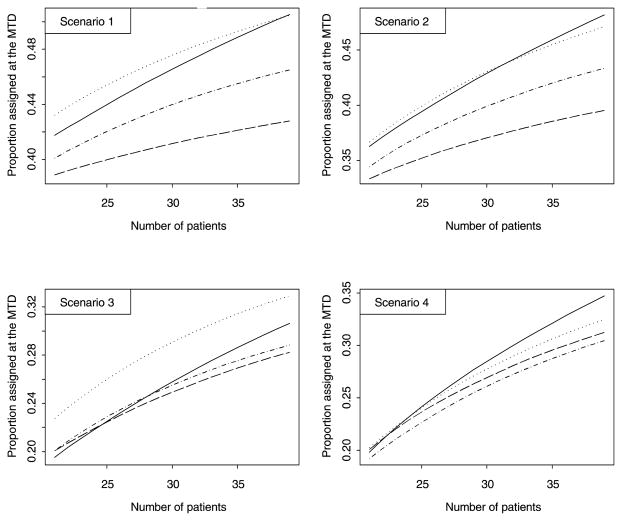
Figure 2.

Proportion of subjects allocated to the MTD for the cumulative cohort decision rule with optimal Δ (solid line), the cumulative cohort decision rule with Δ = 0.01 (dashed line), Leung and Wang’s decision rule (dotted line), and the closest dose decision rule (dotted-dashed line).

The same start-up rule was used for each procedure: Beginning at dose d₁, cohorts of equal size were assigned at escalating doses until the first toxicity is seen, at which time the decision rule from a particular design was initiated. Following Ivanova, Haghighi, Mohanti, and Durham (2003), the cohort size for the start-up was chosen according to the target quantile: cohorts of size 1 for Γ = 0.50, cohorts of size 3 for Γ = 0.25, and cohorts of size 4 for Γ = 0.10.

Tables 2–4 display the percentage of trials in which each dose is selected as the MTD, the average number of subjects assigned to each dose level, and the average number of toxicities in the trial for trials with 30 subjects. The relative performance of the designs does not depend on the target quantile Γ. In short, the cumulative cohort designs perform significantly better in almost all of the scenario/quantile pairs considered, that is, they select the correct MTD more frequently and assign more subjects to the MTD. Both Leung and Wang’s and the “closest dose” designs tend to be very conservative: they assign too many subjects to lower doses.

The cumulative cohort and Yuan and Chappell’s designs select the correct MTD more often than other designs with some advantage of the cumulative cohort design that uses the “optimal” value of Δ. The “optimal” value of Δ was chosen to maximize the number of subjects assigned to the MTD (Ivanova et al. 2007). In 11 out of 12 scenario/quantile configurations the cumulative cohort design with “optimal” Δ assigns more subjects to the MTD compared to the cumulative cohort design with Δ = 0.01. The average number of toxicities for the cumulative cohort design with optimal Δ never exceeds the corresponding number for the cumulative cohort design with Δ = 0.01 except in scenario 4 when Γ = 0.50; in this case the average number of toxicities with “optimal” Δ is significantly lower than is expected when all patients were treated with the MTD. The Yuan and Chappell’s decision rule preformed similar to the cumulative cohort design with “optimal” Δ, but yielded more toxicities.

Figures 1 and 2 displays the designs performance for Γ = 0.25 as the sample size increases from 21 to 39. Figure 1 displays the proportion of trials correctly identifying the MTD. Both cumulative cohort designs perform better by far than Leung and Wang’s rule in selecting the correct MTD. It is interesting to see that, for scenarios 2–4, with each additional subject, the proportion of trials that selected the correct MTD increases by about 1%. Figure 2 displays the proportion of subjects allocated to the MTD. This proportion also increases with the sample size. The cumulative cohort design and Leung and Wang’s decision rule yields comparable proportions assigned to the MTD with Leung and Wang’s decision rule assigning more subjects in scenario 3. Though cumulative cohort designs with “optimal” Δ and with Δ = 0.01 perform similarly, the design with “optimal” Δ assigns more subjects to the MTD and yields less toxicities on average. Hence our recommendation based on this simulation study is to use the cumulative cohort design with “optimal” Δ.

We also studied the performance of the designs with subjects assigned in cohorts of size 3 after the start up. The results were very similar to assignment of subjects one at a time. Hence, it is acceptable to assign subjects in cohorts of not necessarily equal size to shorten the trial duration.

Though the designs are similar in spirit there are distinctions that explain the differences in performance. Consider a trial in which the current dose is d _j and dose d _j+1 has two subjects assigned so far with one of them having toxic response and one nontoxic. The probability of observing one or more toxicities out of two assignments if the true toxicity rate is 0.25 is rather high (0.44). Both the Leung and Wang’s and “closest dose” decision rules will escalate to d _j+1 only if the current estimate of toxicity rate at d _j is 0. The cumulative cohort design with optimal Δ = 0.09 will escalate to d _j+1 if the estimated toxicity rate at d _j is lower than or equal to 0.14. When Γ = 0.50, the “closest dose” decision rule will not escalate to a dose that had a single trial resulting in toxicity. This illustrates the reasons for differences in design performances observed in our simulation study and especially poor performance of the “closest dose” decision rule in the case Γ = 0.50.

4. Discussion

We compared several very intuitive decision rules. The decision rule of Leung and Wang (2001) and the “closest dose” decision rule select the next dose that has estimated toxicity rate closest to the MTD subject to some constraints. The cumulative cohort decision rule repeats the current dose if the estimated toxicity rate at this dose is relatively close to the MTD and changes the dose otherwise.

The decision rule in which the dose closest to the MTD is selected at every step works well in designs where the decision rule is based on estimated toxicity probabilities using a one- or two-parameter model as, for example, in the CRM (O’Quigley et al. 1990). However, our simulations show that the isotonic-based analogs do not work well. One reason is that the data collected at lower doses do not influence the isotonic estimates at higher doses as much as in the case of one-parameter model. In contrast, the parameter Δ in the cumulative cohort design was carefully chosen based on Markov chain theory (Ivanova et al. 2007) to ensure more frequent assignment to the MTD and nearby doses, and our simulations show that this decision rule is clearly superior.

Table 3.

Percent recommendation of each dose as the MTD, the average number of subjects allocated to each dose, and the average number of toxicities in the trial for the cumulative cohort decision rule with optimal Δ = 0.09 (CCD), the cumulative cohort decision rule with Δ = 0.01 (CCD 0), Yuan and Chappell’s decision rule (YC), Leung and Wang’s decision rule (LW), and “closest dose” decision rule (CD). The total sample size is 30. Results at the MTD are in bold. The target is Γ = 0.25

	Percent recommendation						Allocation
	d1	d2	d3	d4	d5	d6	d1	d2	d3	d4	d5	d6	Toxicities
Scenario 1
CCD	0.20	0.70	0.09	0.01	0.00	0.00	10.5	13.7	4.9	0.7	0.2	0.0	7.7
CCD 0	0.17	0.71	0.10	0.01	0.00	0.00	9.8	12.2	6.5	1.2	0.3	0.1	8.4
YC	0.15	0.70	0.14	0.01	0.00	0.00	5.9	12.4	9.0	2.1	0.5	0.1	10.0
LW	0.35	0.58	0.06	0.00	0.00	0.00	11.6	13.9	3.6	0.7	0.2	0.0	7.3
CD	0.40	0.55	0.06	0.00	0.00	0.00	13.0	13.1	3.2	0.6	0.1	0.0	6.9
Scenario 2
CCD	0.00	0.18	0.72	0.10	0.01	0.00	3.6	8.6	12.4	4.5	0.7	0.1	6.8
CCD 0	0.00	0.17	0.70	0.11	0.01	0.00	3.9	8.2	10.9	5.8	1.0	0.2	7.3
YC	0.00	0.14	0.71	0.14	0.01	0.00	3.4	5.3	11.2	7.9	1.8	0.4	8.7
LW	0.03	0.31	0.59	0.07	0.00	0.00	4.0	9.4	12.4	3.4	0.6	0.2	6.3
CD	0.05	0.35	0.54	0.06	0.00	0.00	4.5	10.4	11.6	2.9	0.6	0.1	5.8
Scenario 3
CCD	0.00	0.09	0.34	0.47	0.09	0.01	3.6	7.1	8.6	7.1	3.0	0.6	5.9
CCD 0	0.00	0.06	0.30	0.51	0.12	0.01	3.8	6.2	7.6	7.3	4.2	0.9	6.5
YC	0.00	0.04	0.23	0.60	0.13	0.01	3.4	4.5	5.9	8.3	6.2	1.7	7.8
LW	0.02	0.15	0.36	0.42	0.05	0.00	3.8	6.5	8.5	8.3	2.4	0.6	5.8
CD	0.06	0.19	0.32	0.38	0.05	0.00	4.5	7.6	8.1	7.2	2.2	0.5	5.4
Scenario 4
CCD	0.00	0.00	0.01	0.21	0.56	0.21	3.0	3.3	4.3	6.8	8.1	4.4	4.7
CCD 0	0.00	0.00	0.01	0.20	0.58	0.22	3.0	3.3	4.1	6.5	7.8	5.3	4.9
YC	0.00	0.00	0.00	0.17	0.58	0.25	3.0	3.2	3.5	4.8	7.5	7.9	5.7
LW	0.00	0.01	0.05	0.32	0.46	0.16	3.0	3.3	4.1	7.5	7.8	4.2	4.6
CD	0.00	0.01	0.07	0.34	0.43	0.14	3.0	3.5	4.7	7.9	7.4	3.5	4.3