Accounting for Mating Pair Formation in Plasmid Population Dynamics

Abstract

Plasmids are important vehicles for horizontal gene transfer and rapid adaptation in bacteria, including the spread of antibiotic resistance genes. Conjugative transfer of a plasmid from a plasmid-bearing to a plasmid-free bacterial cell requires contact and attachment of the cells followed by plasmid DNA transfer prior to detachment. We introduce a system of differential equations for plasmid transfer in well-mixed populations that accounts for attachment, DNA transfer, and detachment dynamics. These equations offer advantages over classical mass-action models that combine these three processes into a single “bulk” conjugation rate. By decomposing the process of plasmid transfer into its constituent parts, this new model provides a framework that facilitates meaningful comparisons of plasmid transfer rates in surface and liquid environments. The model also allows one to account for experimental and environmental effects such as mixing intensity. To test the adequacy of the model and further explore the effects of mixing on plasmid transfer, we performed batch culture experiments using three different plasmids and a range of different mixing intensities. The results show that plasmid transfer is optimized at low to moderate shaking speeds and that vigorous shaking negatively affects plasmid transfer. Using reasonable assumptions on attachment and detachment rates, the mathematical model predicts the same behavior.

INTRODUCTION

Of all the mechanisms and mobile elements that mediate horizontal gene transfer between bacteria, conjugation by self-transferable plasmids may well be the most important (Thomas 2000; Thomas and Nielsen 2005; Sota and Top 2008). Particularly salient is the critical role plasmids play in the rapid spread of antibiotic resistance genes (Weigel et al. 2003; Levy and Marshall 2004; McGowan 2006; Welch et al. 2007). While existing mathematical models have greatly improved our insight into the kinetics of plasmid transfer and persistence (Lundquist and Levin 1986; Willms et al. 2006; Krone et al. 2007; Lili et al. 2007; Fox et al. 2008), the assumptions upon which they are based can be further refined. One such assumption is that bacteria in well-mixed environments exist as single cells that randomly collide and then exchange plasmids upon collision, with conjugative transfer rates that essentially average out the effects of certain ignored features of the dynamics.

Plasmid transfer by conjugation requires prolonged “contact” between plasmid-bearing and plasmid-free bacterial cells. Some estimates (Achtman 1975; Andrup et al. 1998; Zechner et al. 2000; Lawley et al. 2002; Babic et al. 2008) suggest that this time for plasmid DNA transfer can be on the order of 3 to 5 minutes for some bacteria-plasmid combinations. In surface-associated populations such as biofilms, the required contact is localized and tends to be quite stable in the absence of strong shear forces. Even in well-mixed liquids, however, bacterial sex doesn’t just happen upon casual contact. Rather, bacterial cells in liquid media form “mating aggregates”–mixed clusters of plasmid-bearing and plasmid-free cells whose prolonged contact is facilitated by fimbriae, sex pili (in Gram-negative species; cf. Achtman 1975), and adhesins (often characteristic of pheromone-producing Gram-positive species; cf. Dunney et al. 1978 and Olmsted et al. 1991). Mating aggregates can consist of two cells (“mating pairs”) or more (for example, up to about 20 cells in E. coli with pilus-producing plasmid F, and pheromone-mediated clumps containing thousands of E. faecalis cells). These mating aggregates can be broken by shear forces.

For conjugation to occur in liquid environments, the plasmid-bearing and plasmid-free cells must successfully complete a 3-step process: first they must collide, then attach, and then conjugate before detachment occurs. Mass-action models lump these components into a single “bulk” conjugation rate that does not explicitly account for factors such as mixing intensity that can affect the dynamics of plasmid transfer. Thus, researchers using different mixing intensities can infer different conjugation rates. Attachment and detachment rates can also be influenced by plasmid-specific factors such as pilus length and flexibility (Bradley et al. 1980).

A typical set of mass-action differential equations tracks the densities of recipients (R), transconjugants (T), and donors (D), as well as nutrient concentration (C). Recipients are plasmid-free cells; donors are the original plasmid-bearing cells in the population and can be either the same strain as the recipient or a different strain. Transconjugants are plasmid-bearing cells that are the same strain as the recipients; they arise when a recipient receives a copy of the plasmid via conjugative transfer from a donor or transconjugant, or through reproduction of transconjugants. (The reason for splitting plasmid-bearing cells into two classes–donors and transconjugants, which carry different markers and hence are easily distinguished in the lab–is to track movement of the plasmid into formerly plasmid-free cells.) An example of a mass-action model that considers only the effects of growth and plasmid transfer in a batch culture is the following (Simonsen et al. 1990; Licht et al. 1999):

$$\{\begin{array}{l}\stackrel{.}{R}={\psi }_R(C)R-{\gamma }_T^{\mathit{bulk}}RT-{\gamma }_D^{\mathit{bulk}}RD\hfill \\ \stackrel{.}{T}={\psi }_T(C)T+{\gamma }_T^{\mathit{bulk}}RT+{\gamma }_D^{\mathit{bulk}}RD\hfill \\ \stackrel{.}{D}={\psi }_D(C)D\hfill \\ \stackrel{.}{C}=-e({\psi }_R(C)R+{\psi }_T(C)T+{\psi }_D(C)D)\hfill \end{array}$$ (1)

where ψ denotes growth rate and γ^bulk conjugation rate, with subscripts indicating cell type. The resource conversion rate, e, specifies the amount of nutrient necessary to make a new cell.

Mass action models and corresponding experiments involving liquid cultures often yield conjugation rate estimates γ^bulk roughly of order 10⁻⁸ to 10⁻¹⁵ under common experimental conditions (Freter et al. 1983; Lundquist and Levin 1986; Simonsen et al. 1990; Gordon 1992; Licht et al. 1999). This contrasts dramatically with the “intrinsic” conjugation rates γ° that refer only to the process of plasmid DNA transfer from one cell to another (Achtman 1975; Andrup et al. 1998; Zechner et al. 2000; Lawley et al. 2002; Babic et al. 2008), and can be of order one or 10 in spatially explicit models (Krone et al. 2007; Fox et al. 2008). At a basic level, this difference is not at all surprising. The intrinsic conjugation rate refers to plasmid transfer from a given donor to a given recipient. In contrast, the “bulk” conjugation rate for a given donor in a mass-action model is meant to be “spread” equally over all potential recipients within a unit of volume (e.g., 10⁸ cells/ml); i.e., all recipients in a mass-action model are considered to be equivalent, whereas in a spatial setting the only potential recipients for a given donor are the ones in close proximity. The bulk conjugation rates of mass-action models are further diminished in relation to intrinsic conjugation rates because they must account for the timing of contact and attachment prior to conjugation.

Our goal in the present study is to account for the fact that, even in well-mixed liquids, conjugation can only occur between attached cells. We explored the ramifications of this fact by introducing a differential equation model that includes attachment and detachment dynamics. We then performed laboratory experiments to determine the effects of mixing intensity on plasmid transfer dynamics for three different plasmids, including two that code for long, flexible pili and one that codes for short, rigid pili. Mathematical predictions based on the model were compared to the empirical results to validate the effectiveness of the model and to help explain the mechanisms underlying the experimental observations.

METHODS

Mathematical model

We developed a “mating pair” differential equation model of plasmid population dynamics, appropriate for well-mixed bacterial populations, such as in liquid cultures, that accounts for the fact that conjugation occurs within mating aggregates. In addition to the nutrient concentration C, and single cell densities R, D, T, that are included in traditional mass-action models, our model also tracks certain attached pair densities. To describe this, we use a “::” between two cell types to indicate that the cells are attached. For example, the collision and attachment phases for R’s and T’s are combined in a rate k₊ TR, and the resulting attached mating pair is denoted by T :: R. Formation of D :: R mating pairs is assumed to occur at rate k₊ DR. We model attachment only of plasmid-bearing with plasmid-free cells; i.e., pairs that have the potential to lead to conjugation events. The model also tracks the attached pairs, T :: T and D :: T, that arise when conjugation occurs in a mating pair. (We reserve the term mating pair to be between plasmid-bearing and plasmid-free cells.) Thus we keep track of all attached pairs that have the potential to lead to a conjugation event or have resulted from a conjugation event; for model simplicity, other attached pairs such as RR and DD are assumed not to form. Let k₋ denote the detachment rate, assumed to be the same for any attached pair. Thus, for example, a T :: R attached pair becomes individual T and R cells at rate k₋.

Let M_TR, M_DR, M_TT, M_DT denote the densities that correspond to attached pairs of the form T :: R, D :: R, T :: T, D :: T, respectively. To simplify the model, we did not consider aggregates of more than two cells. Inclusion of these larger aggregates would dramatically increase the number of equations and states. We provide evidence below that the addition of attached pairs to the standard mass-action models is already enough to capture important sub-processes of conjugation that can be experimentally manipulated. Cell growth rates are assumed to be independent of whether the cells are attached or free (cf. Achtman 1975). To avoid having to deal with aggregates larger than pairs, we assume that reproduction of a cell in an attached pair results in an “offspring” cell of the same type being released to the environment as a single cell.

Let ${\gamma }_D^o$ and ${\gamma }_T^o$ denote the intrinsic conjugation rates (depending on nutrient concentration C) for D and T, respectively, within a mating pair. These intrinsic rates can be thought of as being similar to conjugation rates between neighboring cells on surfaces. Growth rates for R, D, T are denoted ψ_R, ψ_D, ψ_T (all depending on nutrient concentration C) and the resource conversion rate is denoted by e.

The mating pair differential equations governing R, D, T, M_TR, M_DR, M_TT, M_DT (all in units of cells/ml), and C (μg/ml) in batch culture are thus given by

$$\{\begin{array}{l}\stackrel{.}{R}={\psi }_R(C)(R+M_{TR}+M_{DR})+k_{-}(M_{TR}+M_{DR})-k_{+}R(T+D)\hfill \\ \stackrel{.}{T}={\psi }_T(C)(T+M_{TR}+M_{DT}+2M_{TT})+k_{-}(M_{TR}+M_{DT}+2M_{TT})-k_{+}RT\hfill \\ \stackrel{.}{D}={\psi }_D(C)(D+M_{DR}+M_{DT})+k_{-}(M_{DR}+M_{DT})-k_{+}RD\hfill \\ {\stackrel{.}{M}}_{TR}=k_{+}RT-k_{-}{M}_{TR}-{\gamma }_T^o(C)M_{TR}\hfill \\ {\stackrel{.}{M}}_{DR}=k_{+}RD-k_{-}{M}_{DR}-{\gamma }_D^o(C)M_{DR}\hfill \\ {\stackrel{.}{M}}_{TT}={\gamma }_T^o(C)M_{TR}-k_{-}{M}_{TT}\hfill \\ {\stackrel{.}{M}}_{DT}={\gamma }_D^o(C)M_{DR}-k_{-}{M}_{DT}\hfill \\ \begin{array}{l}\stackrel{.}{C}=-e[{\psi }_R(C)(R+M_{TR}+M_{DR})+{\psi }_T(C)(T+M_{TR}+M_{DT}+2M_{TT})\\ +{\psi }_D(C)(D+M_{DR}+M_{DT})]\end{array}\hfill \end{array}$$ (2)

The idea of such models resembling equations for enzyme kinetics was suggested by Andrup et al. (1998). Note that, for simplicity, we have chosen not to explicitly model death rates or segregative plasmid loss. (These were negligible when we applied the model to the short-term experiments below.) These terms can be easily added to the model. It is also easy to adapt the above equations to a chemostat environment by including a washout rate and reservoir nutrient concentration.

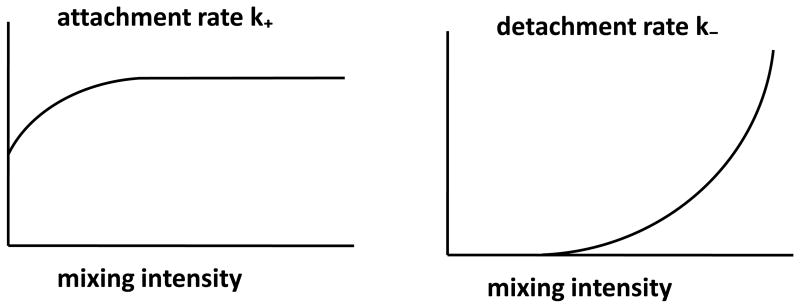
The model parameters are summarized in Table 1. As its units suggest, k₊ is the parameter that comes closest to the classical notion of (bulk) conjugation rate. We show below that the small orders of magnitude observed in bulk conjugation rates are mostly determined by the rate of attachment, while the other components influencing conjugation (i.e., detachment and DNA transfer rates) play a more subtle role. The attachment and detachment rates, k₊ and k₋, are affected by the mixing speed in the liquid, as well as by characteristics of the plasmid and bacterial strains. Intuitively, the more vigorous the mixing, the larger will be k₋ due to an increase in shear force. It has been reported that mating pairs are stable during gentle dilution of the mating cultures (Achtman 1975), suggesting that detachment rate should be approximately zero in a static liquid or under mild mixing conditions. The effect of mixing on k₊ is less obvious, although it is likely that at low mixing speeds an increase in mixing intensity will rapidly increase k₊ due to the enhanced contact; as mixing speeds become higher, however, the rate of contact/attachment probably reaches a point of diminishing returns since the proportion of time during which two cells are in the same small volume will converge to an equilibrium. Due to molecular motion in the liquid, k₊ will be positive even in a static liquid. This is confirmed by the fact that plasmid transfer–not just growth–is observed in unmixed liquid cultures (see “Results”). Figure 1 gives hypothetical curves summarizing the above ideas about attachment and detachment rates.

Table 1.

Model parameters.

Parameter	Definition	Units
ψR, ψD, ψT	growth rates	h−1
${\gamma }_D^o,{\gamma }_T^o$	intrinsic conjugation rates	h−1
k+	attachment rate	ml cell−1 h−1
k−	detachment rate	h−1

Figure 1.

Hypothetical graphs of k₊ and k₋ as functions of mixing intensity.

Experimental materials and methods

We performed batch culture experiments to explore the effects of mixing speed on transconjugant production. Three different plasmids were used in this study: (i) Plasmid pB10 belongs to the incompatibility group IncP, confers resistance to four antibiotics (tetracycline (Tc^R), amoxicillin (Am^R), streptomycin (Sm^R), and sulfonamides (Su^R)) and to mercury chloride (Schlüter et al. 2003). Since IncP plasmids code for short rigid pili, their transfer is typically higher on surfaces than in liquids (Bradley et al. 1980). (ii) F′ is an IncFI plasmid that encodes long flexible pili, is permanently derepressed for conjugation, and contains a Tc^R gene (Tn10) (Bullock et al. 1987). It has recently been shown (Clarke et al. 2008) that these long flexible pili allow donors to efficiently “sample” recipient cells and then to stabilize the contact by retraction. (iii) Plasmid R1, of the IncFII group, also encodes long flexible pili and has been shown to transfer as well in liquids as on surfaces (Bradley et al. 1980). However, it is normally repressed for transfer except for in new transconjugants where transfer is transiently derepressed; it confers resistance to chloramphenicol (Cm^R), kanamycin (Km^R), ampicillin (Amp^R), Sm^R, Su^R (Willetts 1974; Nordstrom et al. 1980; Lundquist and Levin 1986).

E. coli K12 MG1655 (ATCC 47076) was used as the bacterial host. To distinguish donor and recipient strains, two spontaneous mutants, were used: a rifampicin resistant (Rif^R) mutant, K12Rif, and a nalidixic acid resistant (Nal^R) mutant, K12Nal (Fox et al. 2008). The donor strain K12Rif carried the specific plasmid. Strains were grown at 37 °C in Luria-Bertani (LB) medium with appropriate antibiotics: Rif (50 μg/ml) and Tc (10 μg/ml) for donors bearing pB10 and F′, and Rif (50 μg/ml) and Km (50 μg/ml) for R1-carrying donors; Nalidixic acid (Nal) (100 μg/ml) was used for the recipients. F′ and pB10 bearing transconjugants were selected on LB agar with Nal (100 μg/ml) and Tc (10 μg/ml), while R1 bearing transconjugants were plated on LB agar with Nal (100 μg/ml) and Km (50 μg/ml).

For each experiment, donor and recipient strains were grown separately overnight at 37 °C in LB with the appropriate antibiotics. Equal amounts of donor and recipient cells were then mixed. To prepare this initial 50:50 cell mixture, the optical densities (OD600) of the overnight cultures were measured and appropriate culture volumes were taken. The bacterial cells were centrifuged for 1 min at 10,000 × g at room temperature, and the resulting pellets were resuspended in 1 ml of saline solution (NaCl 8.5 g/l) and recentrifuged. The new pellets were resuspended in saline (in a volume determined by the average of the initial culture volumes) and then further diluted 1,000-fold and mixed together in LB. A serial dilution of this suspension was plated on appropriate media to estimate initial bacterial densities. In parallel, 4 ml of the suspension was aliquoted into sterile 50 ml baffled glass flasks (Fisher Sci. Cat. no. 0955242), and incubated at 0, 50, 100, 200, and 300 rpm at 37 °C (0 rpm in Incubator 3EG (Precision Scientific, Winchester, VA); 50 rpm in Shaking Incubator VWR S/P (Sheldon Inc., Cornelius, OR); all others in Innova 4430 Incubator Shakers (New Brunswick Scientific Co., Inc., Edison, NJ)). After 3 hours the cultures were vigorously mixed on a vortex mixer, and appropriate dilutions were plated on LB selection plates using a spiral plater (Spiral Biotech Inc., Norwood, MA). After overnight incubation of the plates at 37 °C, the colonies were counted and the results were presented as colony forming units per milliliter culture (CFU/ml). Plasmid-free recipient counts were obtained by subtracting transconjugant colony counts from the number of colonies obtained on LB agar containing Nal (which included both recipients and transconjugants).

RESULTS

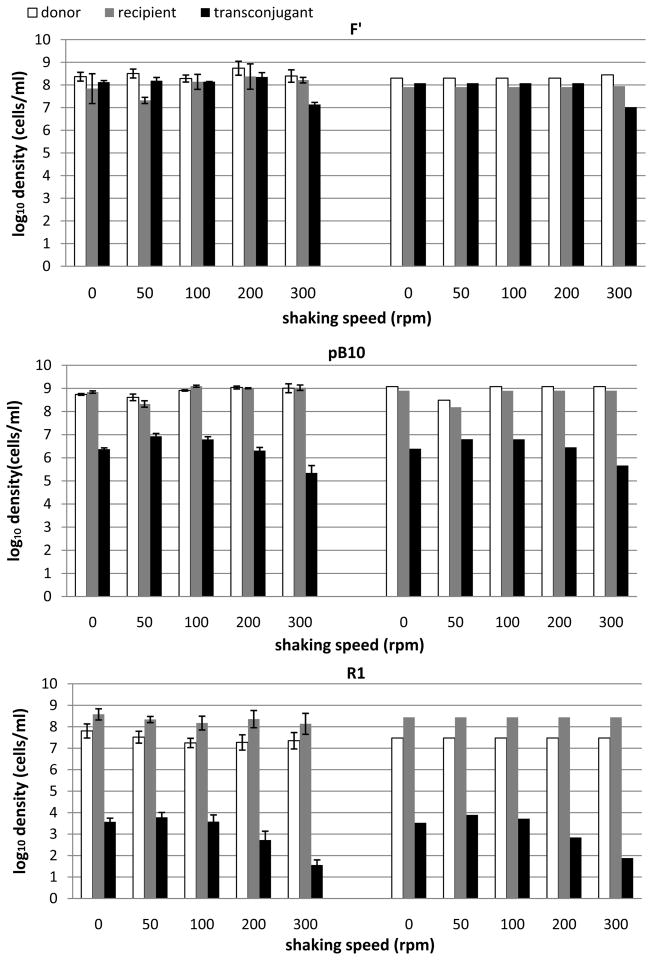
Our mathematical model provides a more detailed description than classical mass-action models of the role of mating pair formation and detachment in conjugative plasmid transfer dynamics. Through numerical solution of the differential equations and experiments that varied mixing intensities, we sought to test (a) whether mixing intensity would affect the amount of plasmid transfer in liquid cultures, and (b) whether the mathematical model would capture these effects. Figure 2 shows densities of donors (D), recipients (R), and transconjugants (T) after 3 hr incubation of donor-recipient mixtures in both experiments and simulations of the mathematical model. The experiments were performed with three different plasmids at shaking speeds ranging from 0 to 300 rpm. Shaking speed was expressed in units of rounds per min (rpm), covering intensities that can be described as static (0 rpm), mild (50–100 rpm), vigorous (200 rpm), and highly vigorous (300 rpm). Even though the correlation between mixing intensity and shaking speed depends on flask and shaker types, these rpm values provide a semi-quantitative measure of actual mixing intensity and shear force. For each plasmid, a one-way analysis of variance showed that the transconjugant densities were not equal across the mixing intensities (p < 0.001), indicating an effect of mixing on plasmid transfer. Follow-up analysis using pairwise comparisons, showed significant differences between the treatment of 300 rpm and the other shaking speeds. Consistently for the three plasmids, the transconjugant yield at 300 rpm was significantly lower than that under any of the other mixing intensities.

Figure 2.

Effects of mixing intensity in experiments (left) and simulations (right) on the formation of transconjugants in LB broth batch cultures for three different plasmids: F′, pB10, and R1. Each experiment/simulation records densities of donors, recipients, and transconjugants after 3 hours of incubation; this includes a lag phase of 0.7 h (during which conjugation occurred, but not growth) and an exponential phase of 2.3 h (during which both growth and conjugation occurred). Initial densities in experiments and simulations: for plasmid F′, R₀ = 2.0 × 10⁶ cells/ml, D₀ = 5.6 × 10⁶ cells/ml; for plasmid pB10, R₀ = 1.6 × 10⁷ cells/ml and D₀ = 2.4 × 10⁷ cells/ml for 0, 100, 200 and 300 rpm, while R₀ = 3.2 × 10⁶ cells/ml and D₀ = 6.2 × 10⁶ cells/ml for 50 rpm; for plasmid R1, R₀ = 6.0 × 10⁵ cells/ml, D₀ = 2.0 × 10⁵ cells/ml. Parameters used in the mathematical model are as in Table 2 and Fig. 3. Error bars in experimental data indicate one standard deviation around the mean.

As shown in Figure 2, the three plasmids consistently showed the highest level of transconjugant production under mild mixing intensity (50–100 rpm) and the lowest level under highly vigorous mixing (300 rpm). The difference between the two levels was about 1–2 orders of magnitude. For plasmid F′, which codes for long flexible pili, transconjugant production was nearly constant over a range of mixing intensities from 0 to 200 rpm (10⁸ cells/ml at the 3 hr sampling time), and fell to 10⁷ cells/ml at 300 rpm. For plasmid pB10, which codes for short rigid pili, transconjugant production changed more with mixing intensity, showing maximum densities at 50 and 100 rpm, lower densities at 0 and 200 rpm, and the lowest at 300 rpm. From 50 rpm to 300 rpm, transconjugant densities fell by a factor of 1/30. While the difference in T between the peak (50–100 rpm) and 0 rpm for pB10 was not statistically significant, repeated experiments always showed the same trend consistent with lower attachment rates when the liquid was not being mixed. Note that the F′ plasmid showed less sensitivity to mixing intensity than pB10.

Even though R1 has long flexible pili, the pattern of transconjugant production was more similar to that of pB10, though at a much lower level. This may be due in part to the fact that pilus synthesis is repressed in most of the R1 transconjugants. We did not include repression dynamics in our model and will treat this in a separate study. However, one can intuitively understand the effect of repression by imagining that many of the T :: R or D :: R mating pairs which form are not “viable” since they cannot lead to conjugation events. We accounted for this in the model through lowered values of k₊. Repression of pilus synthesis may play a role in both attachment and detachment dynamics, but this is not well understood. The actual population dynamics of repression are density dependent, but under some conditions transconjugant production by R1 has been shown to be about 1000-fold lower than that of its permanently derepressed mutant R1drd19 (Dionisio et al. 2002).

Fitting parameters

For a given plasmid, the only experimental variable was shaking speed. We tried to avoid confounding the interpretation of the simulations by keeping most parameters in the model fixed across shaking speeds, and just changing attachment and detachment rates. While this was an approximation, it was consistent with our goal of trying to understand the roles of attachment and detachment. For all three plasmids, the experimental data did not indicate a consistent difference in growth rates between plasmid-bearing and plasmid-free strains, so we assumed all growth rates to be the same, ψ_R = ψ_D = ψ_T, when fitting the model to empirical data. This is also consistent with previous observations (Heuer et al. 2007) that pB10 confers a very small fitness cost to E. coli MG1655 in LB medium. To settle on a value for this common rate, we estimated the growth rate of the recipient strain using a pure culture. The recipient population was sampled every 45 min during exponential phase (0.75 h, 1.5 h, 2.25 h, 3 h). Regression analysis was then applied to find the growth rates 1.45, 1.70 1.78, 1.78, and 1.78 (h⁻¹) for 0 rpm, 50 rpm, 100 rpm, 200 rpm, and 300 rpm, respectively. Since these rates varied only slightly across the five mixing intensities, we used the average value for ψ_R.

Note that the resource conversion rate, e, is not constant in a batch culture since the cells pass through several different physiological states as the population density increases and nutrient is consumed (Baev et al. 2006). To avoid such complications when fitting our differential equations to the empirical data, we chose to restrict our sampling times to three hours. We observed a lag phase for growth of approximately 0.7 h (data not shown), and growth was exponential for the remainder of the first 3 h; there was no observed lag phase for conjugation. We could thus ignore the effect of nutrient concentration on growth rate over this 3 h period; holding growth rate constant at its maximum level during exponential phase also allowed us to dispense with the need for the differential equation describing nutrient level.

The intrinsic conjugation rate was set to 15 for all donors and recipients. This corresponds to a mean time for plasmid DNA transfer of 4 minutes, consistent with times reported in the literature (Achtman 1975; Andrup et al. 1998; Zechner et al. 2000; Lawley et al. 2002; Babic et al. 2008). Table 2 displays the parameter values for growth rates and conjugation rate that were used in the differential equations when attempting to match the experimental data. For at least some plasmids, it has been observed (Andrup and Andersen 1999) that a plasmid-bearing cell that has donated a plasmid must endure a post-conjugation “recovery period” of about 10 minutes before it can transfer to a new recipient, and newly formed transconjugants may require a maturation period of some 40 minutes before they can conjugate. In some models, this might lead one to use a smaller intrinsic conjugation rate (perhaps of order one) that effectively averages out the effects of such delays. In our model, this is not necessary since post-conjugational mating pairs must detach and then attach to new recipients before secondary conjugation can occur.

Table 2.

Parameter values used in simulations.

Plasmid	ψR	ψD	ψT	${\gamma }_D^o={\gamma }_T^o$
F′	1.7	1.7	1.7	15
pB10	1.7	1.7	1.7	15
R1	1.7	1.7	1.7	15

Fitting attachment and detachment rates was more challenging. We began by using a combination of intuition on how mixing speed should change these parameters (see Figure 1), and some simulations of the model to see how the transconjugant density profile was affected by k₊ and k₋ (see below). Figure 2 shows that the effects of mixing on transconjugant production can be accounted for by varying attachment and detachment rates in the model (with constant conjugation rate). F′ codes for long flexible pili which presumably facilitate rapid and stable mating pair formation under most mixing intensities; pB10 codes for short rigid pili that do not reach many cells in the absence of mixing and can break off due to shear stress (Bradley et al. 1980); R1 is repressible, so most of its transconjugants (the repressed ones) cannot form viable mating pairs that lead to plasmid transfer.

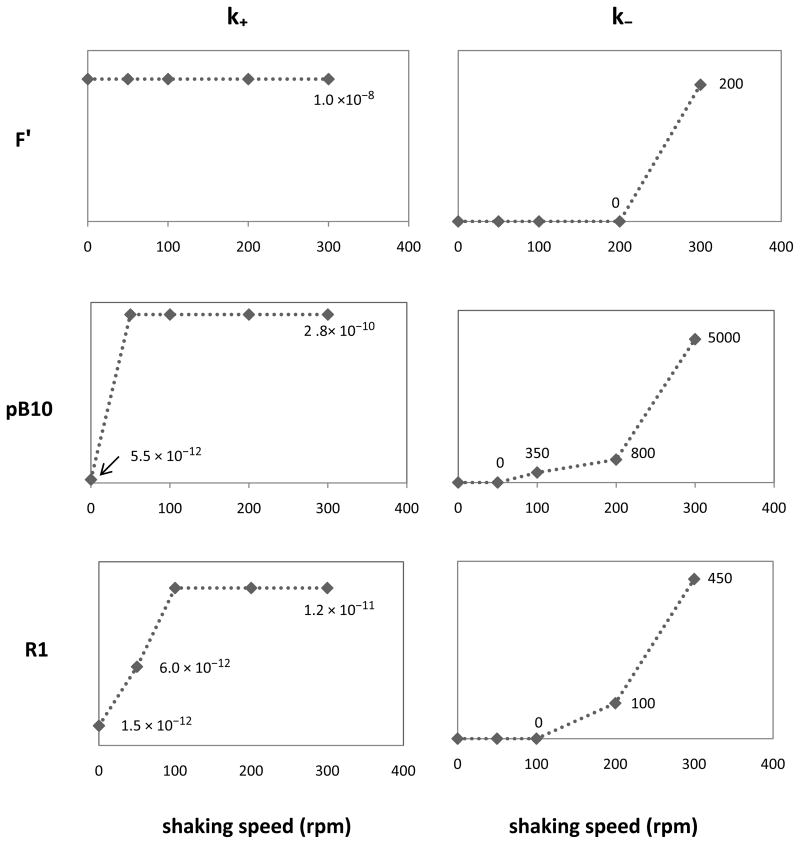
Figure 3 shows the values of k₊ and k₋ used in the simulations summarized in Figure 2. The graphs are mostly consistent with our assumptions (Figure 1) about k₊ and k₋. Transconjugant densities for pB10 and R1 were lower at 0 rpm than at 50 rpm–even though the detachment rate was likely close to 0 for each of these mixing speeds (Achtman 1975). The only way to account for this in the model, while maintaining a detachment rate of 0, was to use a value of k₊ at 0 rpm that was at a lower value than at 50 rpm. Attachment rate k₊ in static liquid was thus slightly lower than that in mixed liquid, but stayed roughly the same as the mixing intensity increased. Only for plasmid F′ was transconjugant production in the static cultures no lower than at higher rpm, possibly owing to its long flexible pili and constitutively expressed mating system (Babic et al. 2008). Thus, k₊ was kept constant over the range of shaking speeds.

Figure 3.

Values of attachment rate k₊ and detachment rate k₋ used in simulations to match experimental data in Fig. 2. Note the different scales of the y-axes for different plasmids.

Note that values of k₊ that were used are roughly of the same order of magnitude as the bulk conjugation rates for the three plasmids. Indeed, when using the endpoint estimate (Simonsen et al. 1990) of bulk conjugation rates from our experimental data at 100 rpm (corresponding to peak transconjugant density) for each of the three plasmids, we saw that this rate is approximately of the same order of magnitude as the k₊ we used in simulations (Table 3). This suggests that, if a given pair of donor and recipient cells are to conjugate in liquid, the attachment phase is by far the most limiting, especially at shaking speeds that are not excessive. Thus, the order of magnitude of observed bulk conjugation rates should be governed mostly by attachment dynamics and a good initial guess for attachment rate (for specific strains of plasmid-bearing and plasmid-free cells, shaking speeds, etc.) is the observed bulk conjugation rate calculated using the endpoint estimate.

Table 3.

Comparison of bulk conjugation rates and k₊ for the 100 rpm data.

Plasmid	γbulk	k+
F′	4.0 × 10−9	1.0 × 10−8
pB10	1.1 × 10−11	2.8 × 10−10
R1	1.9 × 10−11	1.2 × 10−11

The relation between the fitted detachment rates k₋ and shaking speeds was also in accordance with the postulated trend shown in Figure 1. While k₋ remained low for mixing intensities from 0 to 200 rpm, it showed a drastic increase from 200 rpm to 300 rpm. This is consistent with mating pairs breaking up due to strong shear forces at 300 rpm in baffled flasks.

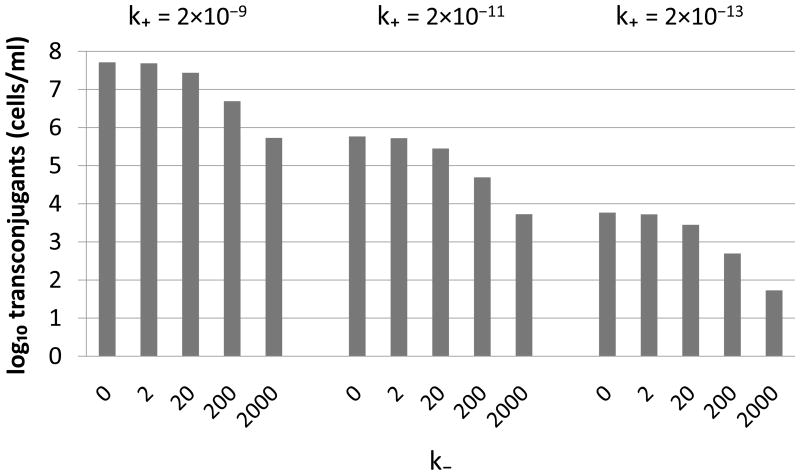
To provide more insight into how the values of k₊ and k₋ were chosen, we show in Figure 4 the simulated behavior of transconjugant densities in response to changes in k₊ and k₋. This confirmed that the attachment rate played a major role in controlling the overall levels of transconjugant production, while the detachment rate affected the shape of the profile as mixing intensity varied.

Figure 4.

Sensitivity of the transconjugant yield (T) to the attachment (k₊) and detachment (k₋) rates. As expected, k₊ and k₋ affected T in opposite directions. Different values of k₊ led to the same profile in transconjugant yield as a function of k₋, but the level was decreased 100-fold for every 100-fold decrease in k₊. Simulations were started with equal numbers of donors and recipients (5×10⁶ cells/ml), and densities were sampled after 3 h (including an initial 0.7 h lag phase for growth). Other parameters: ψ_R = ψ_D = ψ_T = 1.7 h⁻¹, ${\gamma }_D^o={\gamma }_T^o=15{\text{h}}^{-1}$.

Relating bulk and intrinsic conjugation rates

Since transfer only occurs between attached pairs, and estimates of bulk conjugation rates (Simonsen et al. 1990) are based on total R and T densities, we suggest simple “correction” factors that relate bulk and intrinsic conjugation rates:

$${\gamma }_T^{\mathit{bulk}}={\gamma }_T^o{M}_{TR}/R_{\text{tot}}{T}_{\text{tot}}$$ (3)

and

$${\gamma }_D^{\mathit{bulk}}={\gamma }_D^o{M}_{DR}/R_{\text{tot}}{D}_{\text{tot}},$$ (4)

where R_tot, T_tot, and D_tot represent the total numbers (within mating pairs or not) of recipients, transconjugants, and donors, respectively. For example, T_tot = T + M_TR +2M_TT + M_DT. Equation (3) suggests that conjugation from transconjugants to recipients occurs at rate

$${\gamma }_T^{\mathit{bulk}}·R_{\text{tot}}{T}_{\text{tot}}={\gamma }_T^o{M}_{TR}.$$

On the left side of this equation, we have a classical mass-action expression for the rate of increase in transconjugants based on bulk densities and a bulk conjugation rate. On the right side, we have an expression involving only an intrinsic conjugation rate and mating pair densities. The “correction factor” in this case is M_TR/R_totT_tot.

For comparison, we recall that the endpoint estimate (Simonsen et al. 1990), ${\gamma }_{ep}^{\mathit{bulk}}$, of the bulk conjugation rate is given by

$${\gamma }_{ep}^{\mathit{bulk}}={\psi }_{max}·{(N-N_0)}^{-1}ln\left(1+\frac{TN}{DR}\right)$$ (5)

where ψ_max is the estimated maximum per capita growth rate based on total cell densities during exponential phase; R = R(t₁), D = D(t₁), T = T (t₁) are the densities of recipients, donors, and transconjugants at a given sampling time t₁; N = N (t₁) is the total cell density (= R + D + T) at the sampling time and N₀ is the total cell density at time 0. This estimate was derived in a mass-action setting, ignoring mating pairs, and assumes the (bulk) conjugation rates for transconjugants and donors to be the same. It is one of the most commonly used estimates of conjugation rate.

To examine the validity of our proposed links between bulk and intrinsic conjugation rates (equations (3) and (4)), we used the simulated data in Figure 2 to compare these values to those predicted by the endpoint estimate. More specifically, we generated values of M_TR, M_DR, R_tot, T_tot, and D_tot using our mating pair differential equations, with the intrinsic conjugation rates and other parameters as in Table 2 and Figure 3. We then used equations (3) and (4) to compute ${\gamma }_T^{\mathit{bulk}}$ and ${\gamma }_D^{\mathit{bulk}}$, and then equation (5) to compute the endpoint estimate, ${\gamma }_{ep}^{\mathit{bulk}}$. As shown in Table 4, these values are quite close, indicating that the correction factors adequately provide a bridge between two different types of conjugation rate.

Table 4.

Comparison of the bulk conjugation rates predicted by equations (3) and (4) with a standard (endpoint) estimate of bulk conjugation rate. The former use “correction factors” to relate intrinsic conjugation rates to bulk rates.

plasmid	shaking	${\gamma }_T^{\mathit{bulk}}$ (eqn. 3)	${\gamma }_D^{\mathit{bulk}}$ (eqn. 4)	${\gamma }_{ep}^{\mathit{bulk}}$ (eqn. 5)
F ′	0 rpm	3.5 × 10−9	6.1 × 10−9	6.0 × 10−9
	50 rpm	3.5 × 10−9	6.1 × 10−9	6.0 × 10−9
	100 rpm	3.5 × 10−9	6.1 × 10−9	6.0 × 10−9
	200 rpm	3.5 × 10−9	6.1 × 10−9	6.0 × 10−9
	300 rpm	6.7 × 10−10	6.8 × 10−10	6.8 × 10−10
pB10	0 rpm	2.0 × 10−12	4.5 × 10−12	4.5 × 10−12
	50 rpm	1.0 × 10−10	2.3 × 10−10	2.3 × 10−10
	100 rpm	1.1 × 10−11	1.1 × 10−11	1.1 × 10−11
	200 rpm	5.1 × 10−12	5.1 × 10−12	5.1 × 10−12
	300 rpm	8.4 × 10−13	8.4 × 10−13	8.4 × 10−13
R1	0 rpm	4.8 × 10−13	1.2 × 10−12	1.2 × 10−12
	50 rpm	2.2 × 10−12	4.9 × 10−12	4.8 × 10−12
	100 rpm	4.4 × 10−12	9.8 × 10−12	9.6 × 10−12
	200 rpm	1.5 × 10−12	1.5 × 10−12	1.5 × 10−12
	300 rpm	7.6 × 10−13	3.8 × 10−13	3.8 × 10−13

DISCUSSION

This paper serves as a “proof of concept” for a new differential equation model of plasmid population dynamics in mixed bacterial populations. We employed first principles to augment standard mass-action models by including attachment and detachment of cells that participate in mating pair formation. This allowed us to decompose the traditional notion of conjugation rate into components that are differentially affected by experimental conditions such as mixing intensity. This decomposition also provides a unifying framework for understanding differences and similarities between the notions of conjugation rate in spatially structured and well-mixed populations–as, for example, the differences between conjugation dynamics in biofilms and chemostats. For sessile, surface-attached populations, the intrinsic conjugation rate, which is typically of order 1 or 10, is the appropriate notion; for populations in well-mixed liquid media, the intrinsic conjugation rate must be coupled with attachment and detachment rates to account for the fact that “conjugation opportunities” are spread over the entire population instead of being restricted to fixed neighbors. In the case of liquid media, the attachment rate is what determines the small order of magnitude typical of bulk conjugation rates; these values are often of order 10⁻¹⁵ to 10⁻⁸.

To complement these theoretical developments, we empirically examined the effects of mixing intensity on plasmid transfer for three different plasmids in E. coli K12 batch cultures. Transconjugant formation was influenced by mixing intensity, but this mixing effect was plasmid specific. IncP plasmids such as pB10 are known to transfer more efficiently on surfaces than in liquids (Bradley et al. 1980) and, as expected (Frost and Simon 1993), their short rigid pili are more sensitive to changes in shaking speed than F′; F′ transfers at high rates both in liquids and on surfaces because the long flexible pili it encodes help it withstand shear forces (Clarke et al. 2008). The mathematical model was able to capture these features through suitable choices of attachment and detachment rates that reflect–at least in a qualitative sense–the effects of shear forces and pilus type on conjugation. Traditional mass-action models would have required separate estimation of conjugation rates for each of these experimental conditions, without taking into account fluid dynamical differences. Our model thus provides more explanatory and predictive power.

A weakness in our combined experimental/theoretical approach is that we were unable to quantitatively tie mixing intensities to shear force, although shear force certainly should increase with mixing intensity. This problem can be overcome if, for example, one uses a chemostat stirred with an impeller; in this case, there are equations relating shear force to impeller speed (Biggs and Lant 2000). This would permit tighter estimation of detachment rates. Similarly, it should be possible to perform independent experiments to ascertain the effects of pilus type, mixing intensity, etc., on mating pair formation. We did not pursue this alternative experimental protocol, but it is easy to adapt our differential equations to chemostats. Since the above factors can result in orders of magnitude differences in transconjugant levels, even after just three hours, they probably warrant further study.

We remark that the effects of mixing intensity can be highly dependent on the amount of shear force generated since that is one of the primary causes of detachment. Our baffled flasks generated noticeably different levels of agitation at different mixing speeds, and hence different levels of transconjugant production. The use of unbaffled flasks and test tubes, however, resulted in very little change in transconjugant production at different mixing intensities (data not shown) since this stirring was ineffective in breaking up mating pairs. In fact, the liquid tended to swirl around “as a single body” when there were no baffles in the flasks.

Differences in shaking speeds may have other, unintended consequences in addition to differences in mixing intensity. For example, increased shaking in baffled flasks affects dissolved oxygen in the medium. In our experiments, however, growth rates were not affected by shaking speeds. Moreover, since transconjugant densities first increased and then decreased with increased shaking, oxygen levels cannot account for the observed patterns of plasmid transfer. In a separate experiment we observed that the presence or absence of oxygen did not affect the transfer of pB10 between E. coli MG1655 strains during overnight conjugation of aerobically grown pre-cultures on filters in anaerobic conditions (data not shown). It is known that the efficiency of conjugation can be sensitive to temperature (Lilley and Bailey 2002). However, we found no detectable differences in temperature at the different shaking speeds (data not shown).

The mating pair differential equation suggests another phenomenon that could be tested empirically. Plasmids that take longer to transfer their DNA–possibly due to having larger genome size–should be more severely impacted by high mixing intensities than plasmids that transfer their DNA more quickly. In other words, the drop in transconjugant density that we observed at high mixing intensity should be more pronounced when ${\gamma }_T^o$ is smaller. This is because a smaller value of ${\gamma }_T^o$ will result in a larger probability that a T :: R mating pair will detach before plasmid DNA transfer takes place, especially at high mixing intensities where the timing of detachment is more likely to interfere with DNA injection.

Finally, we remark that our experiments are restricted to pilus-mediated plasmid transfer in Gram-negative bacteria and our mathematical model is best suited to such systems with relatively small mating aggregates. However, our model is also likely to provide some much-needed insight into conjugation in Gram-positive bacteria for which aggregation-mediated conjugation systems appear to strongly affect both attachment and detachment dynamics of large mating aggregates (Dunney et al. 1978; Olmsted et al. 1991; Andrup et al. 1998; Andrup and Andersen 1999). Classical mass-action models of plasmid transfer, of course, completely ignore clustering of cells and hence are not well suited to deal with conjugation in these Gram-positive species.