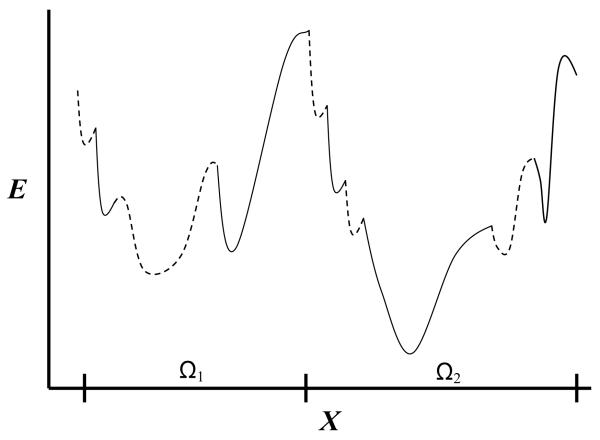
Figure (1).

Schematic one-dimensional representation of part of the energy surface of a peptide or a protein, as a function of a coordinate X. The two large potential energy wells are defined over the corresponding microstates denoted Ω₁ and Ω₂. Each microstate consists of many localized potential wells denoted intermittently by solid and dashed lines. The partition function Z_m of microstate m is obtained by integrating exp[−E/k_BT] over Ω_m where F_m = − k_BT lnZ_m is the microstate’s free energy. The figure suggests that the second microstate is the more stable among the two due to lower energy and higher entropy (Ω₂ is larger than Ω₁) hence lower free energy. If F₂ is also the global free energy minimum of a protein, Ω₂ is expected to describe the native microstate (assuming a perfect force field) and a simulation started from Ω₂ will keep the protein in this microstate for a long time. On the other hand, a peptide can populate significantly several of the most stable microstates in thermodynamic equilibrium.