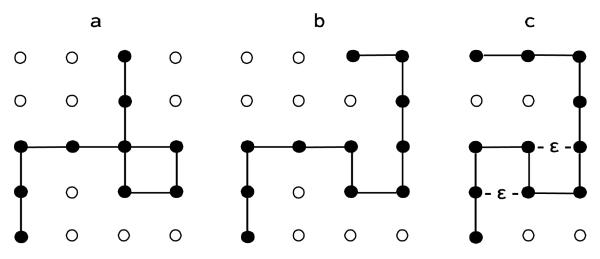
Figure 2.

(a) An ideal chain of N=10 bonds (steps) and 11 monomers (full spheres) on a large square lattice, which only a limited part of it appears in the figure. The chain can intersect itself and go on itself. Because attraction energy is not defined all chains have the same Boltzmann probability, P_i^B (equation (5)). The ensemble of ideal chains can be generated (as random walks) step-by-step (from nothing) where a direction (out of 4 available directions) is selected blindly with transition probability (TP) 1/4. Therefore, the Boltzmann probability of an ideal chain is P_i^B =(1/4)^N and the entropy is k_BNln4. (b) A self-avoiding walk (SAW); here the excluded volume interaction is applied, i.e., self-intersections are not allowed. Thus, the ensemble of SAWs constitutes a partial group of the ideal chains. Again, all SAWs have the same Boltzmann probability, however P_i^B is unknown exactly. One can build the ensemble of SAWs step-by-step blindly, discarding the produced self-intersection chains and retaining only the SAWs; the entropy can be calculated but the procedure is extremely inefficient; in practice, SAWs of length larger than N=100 cannot be generated because the number of self-intersecting walks increases exponentially with N. With the exact scanning method, the transition probabilities (TPs) at each step are calculated by scanning all possible (SAW) continuations of the chain in future steps. This guarantees that the chain will not get into traps (dead ends) in future steps; the entropy is calculated exactly as a logarithm of the product of the transition probabilities (equation (10)). (c) A self-interacting SAW. Two (non-bonded) monomers that are nearest neighbors on the lattice interact with a negative energy ε (ε = −| ε|) (see equation (14) and equations (20)-(35)).