A unifying framework for seed sensitivity and its application to subset seeds

Abstract

We propose a general approach to compute the seed sensitivity, that can be applied to different definitions of seeds. It treats separately three components of the seed sensitivity problem – a set of target alignments, an associated probability distribution, and a seed model – that are specified by distinct finite automata. The approach is then applied to a new concept of subset seeds for which we propose an efficient automaton construction. Experimental results confirm that sensitive subset seeds can be efficiently designed using our approach, and can then be used in similarity search producing better results than ordinary spaced seeds.

1. Introduction

In the framework of pattern matching and similarity search in biological sequences, seeds specify a class of short sequence motif which, if shared by two sequences, are assumed to witness a potential similarity. Spaced seeds have been introduced several years ago [8, 18] and have been shown to improve significantly the efficiency of the search. One of the key problems associated with spaced seeds is a precise estimation of the sensitivity of the associated search method. This is important for comparing seeds and for choosing most appropriate seeds for a sequence comparison problem to solve.

The problem of seed sensitivity depends on several components. First, it depends on the seed model specifying the class of allowed seeds and the way that seeds match (hit) potential alignments. In the basic case, seeds are specified by binary words of certain length (span), possibly with a constraint on the number of 1’s (weight). However, different extensions of this basic seed model have been proposed in the literature, such as multi-seed (or multi-hit) strategies [2, 14, 18], seed families [17, 20, 23, 16, 22, 6], seeds over non-binary alphabets [9, 19], vector seeds [4, 6].

The second parameter is the class of target alignments that are alignment fragments that one aims to detect. Usually, these are gapless alignments of a given length. Gapless alignments are easy to model, in the simplest case they are represented by binary sequences in the match/mismatch alphabet. This representation has been adopted by many authors [18, 13, 5, 10, 7, 11]. The binary representation, however, cannot distinguish between different types of matches and mismatches, and is clearly insufficient in the case of protein sequences. In [4, 6], an alignment is represented by a sequence of real numbers that are scores of matches or mismatches at corresponding positions. A related, but yet different approach is suggested in [19], where DNA alignments are represented by sequences on the ternary alphabet of match/transition/transversion. Finally, another generalization of simple binary sequences was considered in [15], where alignments are required to be homogeneous, i.e. to contain no sub-alignment with a score larger than the entire alignment.

The third necessary ingredient for seed sensitivity estimation is the probability distribution on the set of target alignments. Again, in the simplest case, alignment sequences are assumed to obey a Bernoulli model [18, 10]. In more general settings, Markov or Hidden Markov models are considered [7, 5]. A different way of defining probabilities on binary alignments has been taken in [15]: all homogeneous alignments of a given length are considered equiprobable.

Several algorithms for computing the seed sensitivity for different frameworks have been proposed in the above-mentioned papers. All of them, however, use a common dynamic programming (DP) approach, first brought up in [13].

In the present paper, we propose a general approach to computing the seed sensitivity. This approach subsumes the cases considered in the above-mentioned papers, and allows to deal with new combinations of the three seed sensitivity parameters. The underlying idea of our approach is to specify each of the three components – the seed, the set of target alignments, and the probability distribution – by a separate finite automaton.

A deterministic finite automaton (DFA) that recognizes all alignments matched by given seeds was already used in [7] for the case of ordinary spaced seeds. In this paper, we assume that the set of target alignments is also specified by a DFA and, more importantly, that the probabilistic model is specified by a probability transducer – a probability-generating finite automaton equivalent to HMM with respect to the class of generated probability distributions.

We show that once these three automata are set, the seed sensitivity can be computed by a unique general algorithm. This algorithm reduces the problem to a computation of the total weight over all paths in an acyclic graph corresponding to the automaton resulting from the product of the three automata. This computation can be done by a well-known dynamic programming algorithm [21, 12] with the time complexity proportional to the number of transitions of the resulting automaton. Interestingly, all above-mentioned seed sensitivity algorithms considered by different authors can be reformulated as instances of this general algorithm.

In the second part of this work, we study a new concept of subset seeds – an extension of spaced seeds that allows to deal with a non-binary alignment alphabet and, on the other hand, still allows an efficient hashing method to locate seeds. For this definition of seeds, we define a DFA with a number of states independent of the size of the alignment alphabet. Reduced to the case of ordinary spaced seeds, this DFA construction gives the same worst-case number of states as the Aho-Corasick DFA used in [7]. Moreover, our DFA has always no more states than the DFA of [7], and has substantially less states on average.

Together with the general approach proposed in the first part, our DFA gives an efficient algorithm for computing the sensitivity of subset seeds, for different classes of target alignments and different probability transducers. In the experimental part of this work, we confirm this by running an implementation of our algorithm in order to design efficient subset seeds for different probabilistic models, trained on real genomic data. We also show experimentally that designed subset seeds allow to find more significant alignments than ordinary spaced seeds of equivalent selectivity.

2. General Framework

Estimating the seed sensitivity amounts to compute the probability for a random word (target alignment), drawn according to a given probabilistic model, to belong to a given language, namely the language of all alignments matched by a given seed (or a set of seeds).

2.1. Target Alignments

Target alignments are represented by words over an alignment alphabet . In the simplest case, considered most often, the alphabet is binary and expresses a match or a mismatch occurring at each alignment column. However, it could be useful to consider larger alphabets, such as the ternary alphabet of match/transition/transversion for the case of DNA (see [19]). The importance of this extension is even more evident for the protein case ([6]), where different types of amino acid pairs are generally distinguished.

Usually, the set of target alignments is a finite set. In the case considered most often [18, 13, 5, 10, 7, 11], target alignments are all words of a given length n. This set is trivially a regular language that can be specified by a deterministic automaton with (n + 1) states. However, more complex definitions of target alignments have been considered (see e.g. [15]) that aim to capture more adequately properties of biologically relevant alignments. In general, we assume that the set of target alignments is a finite regular language L_T ∈ 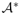and thus can be represented by an acyclic DFA $T=<Q_T,q_T^0,q_T^F,𝒜,{\psi }_T>$.

2.2. Probability Assignment

Once an alignment language L_T has been set, we have to define a probability distribution on the words of L_T. We do this using probability transducers.

A probability transducer is a finite automaton without final states in which each transition outputs a probability.

Definition 1

A probability transducer G over an alphabet is a 4-tuple $<Q_G,q_G^0,𝒜,{\rho }_G>$ , where Q_G is a finite set of states, $q_G^0\in Q_G$ is an initial state, and ρ_G: Q_G × × Q_G → [0, 1] is a real-valued probability function such that

$$\forall q\in Q_G,{\sum }_{q^{\prime }\in Q_G,a\in 𝒜}{\rho }_G(q,a,q^{\prime })=1.$$

A transition of G is a triplet e =< q, a, q′ > such that ρ(q, a, q′) > 0. Letter a is called the label of e and denoted label (e). A probability transducer G is deterministic if for each q ∈ Q_G and each a ∈ , there is at most one transition < q, a, q′ >. For each path P = (e₁, …, e_n) in G, we define its label to be the word label(P) = label(e₁)…label(e_n), and the associated probability to be the product $\rho (P)={\prod }_{i=1}^n{\rho }_G(e_i)$. A path is initial, if its start state is the initial state $q_G^0$ of the transducer G.

Definition 2

The probability of a word w ∈ 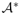according to a probability transducer $G=<Q_G,q_G^0,𝒜,{\rho }_G>$, denoted 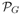(w), is the sum of probabilities of all initial paths in G with the label w. 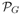(w) = 0 if no such path exists. The probability 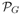(L) of a finite language L ⊆ 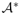according a probability transducer G is defined by 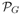(L) = Σ_w∈L 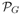(w).

Note that for any n and for L = Aⁿ (all words of length n), 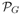(L) = 1.

Probability transducers can express common probability distributions on words (alignments). Bernoulli sequences with independent probabilities of each symbol [18, 10, 11] can be specified with deterministic one-state probability transducers. In Markov sequences of order k [7, 20], the probability of each symbol depends on k previous symbols. They can therefore be specified by a deterministic probability transducer with at most ||^k states.

A Hidden Markov model (HMM) [5] corresponds, in general, to a non-deterministic probability transducer. The states of this transducer correspond to the (hidden) states of the HMM, plus possibly an additional initial state. Inversely, for each probability transducer, one can construct an HMM generating the same probability distribution on words. Therefore, non-deterministic probability transducers and HMMs are equivalent with respect to the class of generated probability distributions. The proofs are straightforward and are omitted due to space limitations.

2.3. Seed automata and seed sensitivity

Since the advent of spaced seeds [8, 18], different extensions of this idea have been proposed in the literature (see Introduction). For all of them, the set of possible alignment fragments matched by a seed (or by a set of seeds) is a finite set, and therefore the set of matched alignments is a regular language. For the original spaced seed model, this observation was used by Buhler et al. [7] who proposed an algorithm for computing the seed sensitivity based on a DFA defining the language of alignments matched by the seed. In this paper, we extend this approach to a general one that allows a uniform computation of seed sensitivity for a wide class of settings including different probability distributions on target alignments, as well as different seed definitions.

Consider a seed (or a set of seeds) π under a given seed model. We assume that the set of alignments L_π matched by π is a regular language recognized by a DFA $S_{\pi }=<Q_S,q_S^0,Q_S^F,𝒜,{\psi }_S>$. Consider a finite set L_T of target alignments and a probability transducer G. Under this assumptions, the sensitivity of π is defined as the conditional probability

$$\frac{{\mathcal{P}}_G(L_T\cap L_{\pi })}{{\mathcal{P}}_G(L_T)}.$$ (1)

An automaton recognizing L = L_T ∩ L_π can be obtained as the product of automata T and S_π recognizing L_T and L_π respectively. Let $K=<Q_K,q_K^0,Q_K^F,𝒜,{\psi }_K>$ be this automaton. We now consider the product W of K and G, denoted K × G, defined as follows.

Definition 3

Given a DFA $K=<Q_K,q_K^0,Q_K^F,𝒜,{\psi }_K>$ and a probability transducer $G=<Q_G,q_G^0,𝒜,{\rho }_G>$, the product of K and G is the probability-weighted automaton $W=<Q_W,q_W^0,Q_W^F,𝒜,{\rho }_W>$ (for short, PW-automaton) such that

• Q_W = Q_K × Q_G,

• $q_W^0=(q_K^0,q_G^0)$,

• $q_W^F=\{(q_K,q_G)\mid q_K\in Q_K^F\}$,

• ${\rho }_W((q_K,q_G),a,(q_K^{\prime },q_G^{\prime }))=\{\begin{array}{ll}{\rho }_G(q_G,a,q_G^{\prime }\hfill & \text{if}{\psi }_k(q_K,a)=q_K^{\prime },\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$

W can be viewed as a non-deterministic probability transducer with final states. ${\rho }_W((q_K,q_G),a,(q_K^{\prime },q_G^{\prime }))$ is the probability of the transition $<(q_K,q_G),a,(q_K^{\prime },q_G^{\prime })>$ A path in W is called full if it goes from the initial to a final state.

Lemma 4

Let G be a probability transducer. Let L be a finite language and K be a deterministic automaton recognizing L. Let W = G × K. The probability 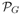(L) is equal to sum of probabilities of all full paths in W.

Proof.

Since K is a deterministic automaton, each word w ∈ L corresponds to a single accepting path in K and the paths in G labeled w (see Definition 1) are in one-to-one correspondence with the full path in W accepting w. By definition, 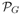(w) is equal to the sum of probabilities of all paths in G labeled w. Each such path corresponds to a unique path in W, with the same probability. Therefore, the probability of w is the sum of probabilities of corresponding paths in W. Each such path is a full path, and paths for distinct words w are disjoint. The lemma follows.

2.4. Computing Seed Sensitivity

Lemma 4 reduces the computation of seed sensitivity to a computation of the sum of probabilities of paths in a PW-automaton.

Lemma 5

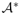Consider an alignment alphabet , a finite set L_T ⊆ of target alignments, and a set L_π ⊆ 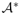of all alignments matched by a given seed π. Let $K=<Q_K,q_t^0,Q_K^F,𝒜,{\psi }_Q>$ be an acyclic DFA recognizing the language L = L_T ∩ L_π. Let further $G=<Q_G,q_G^0,𝒜,\rho >$ be a probability transducer defining a probability distribution on the set L_T. Then 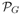(L) can be computed in time

$$\vartheta (\mid Q_G{\mid }^2·\mid Q_K\mid ·\mid 𝒜\mid )$$ (2)

and space

$$\vartheta (\mid Q_G\mid ·\mid Q_K\mid ).$$ (3)

Proof.

By Lemma 4, the probability of L with respect to G can be computed as the sum of probabilities of all full paths in W. Since K is an acyclic automaton, so is W. Therefore, the sum of probabilities of all full paths in W leading to final states $q_W^F$ can be computed by a classical DP algorithm [21] applied to acyclic directed graphs ([12] presents a survey of application of this technique to different bioinformatic problems). The time complexity of the algorithm is proportional to the number of transitions in W. W has |Q_G| · |Q_K| states, and for each letter of , each state has at most |Q_G| outgoing transitions. The bounds follow.

Lemma 5 provides a general approach to compute the seed sensitivity. To apply the approach, one has to define three automata:

• a deterministic acyclic DFA T specifying a set of target alignments over an alphabet (e.g. all words of a given length, possibly verifying some additional properties),

• a (generally non-deterministic) probability transducer G specifying a probability distribution on target alignments (e.g. Bernoulli model, Markov sequence of order k, HMM),

• a deterministic DFA S_π specifying the seed model via a set of matched alignments.

As soon as these three automata are defined, Lemma 5 can be used to compute probabilities 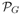(L_T ∩ L_π) and 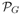(L_T) in order to estimate the seed sensitivity according to (1).

Note that if the probability transducer G is deterministic (as it is the case for Bernoulli models or Markov sequences), then the time complexity (2) is 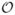(|Q_G| · |Q_K| · ||). In general, the complexity of the algorithm can be improved by reducing the involved automata. Buhler et al. [7] introduced the idea of using the Aho-Corasick automaton [1] as the seed automaton S_π for a spaced seed. The authors of [7] considered all binary alignments of a fixed length n distributed according to a Markov model of order k. In this setting, the obtained complexity was 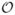(w2^s−w2^kn), where s and w are seed’s span and weight respectively. Given that the size of the Aho-Corasick automaton is 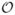(w2^s−w), this complexity is automatically implied by Lemma 5, as the size of the probability transducer is 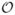(2^k), and that of the target alignment automaton is 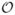(n). Compared to [7], our approach explicitly distinguishes the descriptions of matched alignments and their probabilities, which allows us to automatically extend the algorithm to more general cases.

Note that the idea of using the Aho-Corasick automaton can be applied to more general seed models than individual spaced seeds (e.g. to multiple spaced seeds, as pointed out in [7]). In fact, all currently proposed seed models can be described by a finite set of matched alignment fragments, for which the Aho-Corasick automaton can be constructed. We will use this remark in later sections.

The sensitivity of a spaced seed with respect to an HMM-specified probability distribution over binary target alignments of a given length n was studied by Brejova et al. [5]. The DP algorithm of [5] has a lot in common with the algorithm implied by Lemma 5. In particular, the states of the algorithm of [5] are triples < w, q, m >, where w is a prefix of the seed π, q is a state of the HMM, and m ∈ [0..n]. The states therefore correspond to the construction implied by Lemma 5. However, the authors of [5] do not consider any automata, which does not allow to optimize the preprocessing step (counterpart of the automaton construction) and, on the other hand, does not allow to extend the algorithm to more general seed models and/or different sets of target alignments.

A key to an efficient solution of the sensitivity problem remains the definition of the seed. It should be expressive enough to be able to take into account properties of biological sequences. On the other hand, it should be simple enough to be able to locate seeds fast and to get an efficient algorithm for computing seed sensitivity. According to the approach presented in this section, the latter is directly related to the size of a DFA specifying the seed.

3. Subset seeds

3.1. Definition

Ordinary spaced seeds use the simplest possible binary “match-mismatch” alignment model that allows an efficient implementation by hashing all occurring combinations of matching positions. A powerful generalization of spaced seeds, called vector seeds, has been introduced in [4]. Vector seeds allow one to use an arbitrary alignment alphabet and, on the other hand, provide a flexible definition of a hit based on a cooperative contribution of seed positions. A much higher expressiveness of vector seeds lead to more complicated algorithms and, in particular, prevents the application of direct hashing methods at the seed location stage.

In this section, we consider subset seeds that have an intermediate expressiveness between spaced and vector seeds. It allows an arbitrary alignment alphabet and, on the other hand, still allows using a direct hashing for locating seed, which maps each string to a unique entry of the hash table. We also propose a construction of a seed automaton for subset seeds, different from the Aho-Corasick automaton. The automaton has 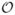(w2^s−w) states regardless of the size of the alignment alphabet, where s and w are respectively the span of the seed and the number of “must-match” positions. From the general algorithmic framework presented in the previous section (Lemma 5), this implies that the seed sensitivity can be computed for subset seeds with same complexity as for ordinary spaced seeds. Note also that for the binary alignment alphabet, this bound is the same as the one implied by the Aho-Corasick automaton. However, for larger alphabets, the Aho-Corasick construction leads to 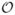(w||^s−w) states. In the experimental part of this paper (section 4.1) we will show that even for the binary alphabet, our automaton construction yields a smaller number of states in practice.

Consider an alignment alphabet . We always assume that contains a symbol 1, interpreted as “match”. A subset seed is defined as a word over a seed alphabet ℬ, such that

• letters of ℬ denote subsets of the alignment alphabet containing 1 (ℬ ⊆ {1} ∪ 2),

• ℬ contains a letter # that denotes subset {1},

• a subset seed b₁b₂ … b_m ∈ ℬ^m matches an alignment fragment a₁a₂ … a_m ∈ 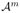if ∀i ∈ [1..m], a_i ∈ b_i.

The #-weight of a subset seed π is the number of # in π and the span of π is its length.

Example 1

[19] considered the alignment alphabet = {1, h, 0} representing respectively a match, a transition mismatch, or a transversion mismatch in a DNA sequence alignment. The seed alphabet is ℬ = {#,@,_} denoting respectively subsets {1}, {1, h}, and {1, h, 0}. Thus, seed π = #@_# matches alignment s = 10h1h1101 at positions 4 and 6. The span of π is 4, and the #-weight of π is 2.

Note that unlike the weight of ordinary spaced seeds, the #-weight cannot serve as a measure of seed selectivity. In the above example, symbol @ should be assigned weight 0.5, so that the weight of π is equal to 2.5 (see [19]).

3.2. Subset Seed Automaton

Let us fix an alignment alphabet , a seed alphabet ℬ, and a seed π = π₁π₂ … π_m ∈ ℬ* of span m and #-weight w. Let R_π be the set of all non-# positions in π, |R_π| = r = m − w. We now define an automaton S_π =<Q, q₀, Q_f, , ψ: Q × → Q> that recognizes the set of all alignments matched by π.

The states Q of S_π are pairs < X, t > such that X ⊆ R_π, t ∈ [0,…, m], with the following invariant condition. Suppose that S_π has read a prefix s₁ … s_p of an alignment s and has come to a state < X, t >. Then t is the length of the longest suffix of s₁ … s_p of the form 1ⁱ, i ≤ m, and X contains all positions xi ∈ R_π such that prefix π₁ … π_xi of π matches a suffix of s₁ … s_p−t.

Example 2

In the framework of Example 1, consider a seed π and an alignment prefix s of length p = 11 given on Figure 1(a) and (b) respectively. The length t of the last run of 1’s of s is 2. The last mismatch position of s is s₉ = h. The set R_π of non-# positions of π is {2, 4, 7} and π has 3 prefixes ending at positions of R_π (Figure 1(c)). Prefixes π_1..2 and π_1..7 do match suffixes of s₁s₂ … s₉, and prefix π_1..4 does not. Thus, the state of the automaton after reading s₁s₂ … s₁₁ is < {2, 7}, 2 >.

Figure 1.

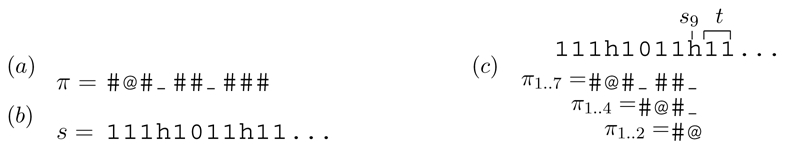
Illustration to Example 2

The initial state q₀ of S_π is the state < ∅,0 >. The final states Q_f of S_π are all states q =< X, t >, where max{X} + t = m. All final states are merged into one state.

The transition function ψ(q, a) is defined as follows: If q is a final state, then ∀_a ∈ , ψ(q, a) = q. If q =< X, t > is a non-final state, then

• if a = 1 then ψ(q, a) =< X, t + 1 >,

• otherwise ψ(q, a) =< X_U ∪ X_V, 0 > with

  • – X_U = {x|x ≤ t + 1 and a matches π_x}

  • – X_V = {x + t + 1|x ∈ X and a matches π_x+t+1}

Lemma 6

The automaton S_π accepts the set of all alignments matched by π.

Proof.

It can be verified by induction that the invariant condition on the states < X, t > ∈ Q is preserved by the transition function ψ. The final states verify max{X} + t = m, which implies that π matches a suffix of s₁ … s_p.

Lemma 7

The number of states of the automaton S_π is no more than (w + 1)2^r.

Proof.

Assume that R_π = {x₁, x₂, …, x_r} and x₁ < x₂ … < x_r. Let Q_i be the set of non-final states < X, t > with max{X} = x_i, i ∈ [1..r]. For states q =< X, t >∈ Q_i there are 2ⁱ⁻¹ possible values of X and m − x_i possible values of t, as max{X} + t ≤ m − 1.

Thus,

$$\mid Q_i\mid \le 2^{i-1}(m-x_i)\le 2^{i-1}(m-i),\text{and}$$ (4)

$$\sum _{i=1}^r\mid Q_i\mid \le \sum _{i=1}^r{2}^{i-1}(m-i)=(m-r+1)2^r-m-1.$$ (5)

Besides states Q_i, Q contains m states < ∅, t > (t ∈ [0..m − 1]) and one final state. Thus, |Q| ≤ (m − r + l)2^r = (w + l)2^r.

Note that if π starts with #, which is always the case for ordinary spaced seeds, then X_i ≥ i + 1, i ∈ [1..r], and the bound of (4) rewrites to 2ⁱ⁻¹(m − i − 1). This results in the same number of states w2^r as for the Aho-Corasick automaton [7]. The construction of automaton S_π is optimal, in the sense that no two states can be merged in general, as the following Lemma states.

Lemma 8

Consider a spaced seed π which consists of two “must-match” symbols # separated by r jokers. Then the automaton S_π is reduced, that is any non-final state is reachable from the initial state q₀, and any two non-final states q, q′ are non-equivalent.

Proof.

See appendix A.

A straightforward generation of the transition table of the automaton S_π can be performed in time 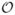(r · w · 2^r · ||). A more complicated algorithm allows one to reduce the bound to 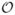(w · 2^r · ||). This algorithm is described in full details in Appendix B. Here we summarize it in the following Lemma.

Lemma 9

The transition table of automaton S_π can be constructed in time proportional to its size, which is 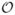(w · 2^r · ||).

In the next section, we demonstrate experimentally that on average, our construction yields a very compact automaton, close to the minimal one. Together with the general approach of section 2, this provides a fast algorithm for computing the sensitivity of subset seeds and, in turn, allows to perform an efficient design of spaced seeds well-adapted to the similarity search problem under interest.

4. Experiments

Several types of experiments have been performed to test the practical applicability of the results of sections 2,3. We focused on DNA similarity search, and set the alignment alphabet to {1, h, 0} (match, transition, transversion). For subset seeds, the seed alphabet ℬ was set to {#, @, _}, where # = {1}, @ = {1, h}, _= {1, h, 0} (see Example 1). The weight of a subset seed is computed by assigning weights 1, 0.5 and 0 to symbols #, @ and _ respectively.

4.1. Size of the automaton

We compared the size of the automaton S_π defined in section 3 and the Aho-Corasick automaton [1], both for ordinary spaced seeds (binary seed alphabet) and for subset seeds. The Aho-Corasick automaton for spaced seeds was constructed as defined in [7]. For subset seeds, a straightforward generalization was considered: the Aho-Corasick construction was applied to the set of alignment fragments matched by the seed.

Tables 1(a) and 1(b) present the results for spaced seeds and subset seeds respectively. For each seed weight w, we computed the average number of states (avg. size) of the Aho-Corasick automaton and our automaton S_π, and reported the corresponding ratio (δ) with respect to the average number of states of the minimized automaton. The average was computed over all seeds of span up to w + 8 for spaced seeds and all seeds of span up to w + 5 with two @’s for subset seeds. Interestingly, our automaton turns out to be more compact than the Aho-Corasick automaton not only on non-binary alphabets (which was expected), but also on the binary alphabet (cf Table 1(a)). Note that for a given seed, one can define a surjective mapping from the states of the Aho-Corasick automaton onto the states of our automaton. This implies that our automaton has always no more states than the Aho-Corasick automaton.

Table 1.

Comparison of the average number of states of Aho-Corasick automaton, automaton S_π of section 3 and minimized automaton

Spaced	Aho-Corasick		Sπ		Minimized
w	avg. size	δ	avg. size	δ	avg. size
9	345.94	3.06	146.28	1.29	113.21
10	380.90	3.16	155.11	1.29	120.61
11	415.37	3.25	163.81	1.28	127.62
12	449.47	3.33	172.38	1.28	134.91
13	483,27	3.41	180.89	1.28	141.84
(a)

Subset	Aho-Corasick		Sπ		Minimized
w	avg. size	δ	avg. size	δ	avg. size
9	1900.65	15.97	167.63	1.41	119,00
10	2103.99	16.50	177.92	1.40	127.49
11	2306.32	16.96	188.05	1.38	135.95
12	2507.85	17.42	198.12	1.38	144.00
13	2709.01	17.78	208.10	1.37	152.29
(b)

4.2. Seed Design

In this part, we considered several probability transducers to design spaced or subset seeds. The target alignments included all alignments of length 64 on alphabet {1, h, 0}. Four probability transducers have been studied (analogous to those introduced in [3]):

• B: Bernoulli model

• DT1: deterministic probability transducer specifying probabilities of {1, h, 0} at each codon position (extension of the M⁽³⁾ model of [3] to the three-letter alphabet),

• DT2: deterministic probability transducer specifying probabilities of each of the 27 codon instances {1, h, 0}³ (extension of the M⁽⁸⁾ model of [3] to the three-letter alphabet),

• NT: non-deterministic probability transducer combining four copies of DT2 specifying four distinct codon conservation levels (called HMM model in [3]).

Models DT1, DT2 and NT have been trained on alignments resulting from a pairwise comparison of 40 bacteria genomes. Details of the training procedure as well as the resulting parameter values are given in Appendix C.

For each of the four probability transducers, we computed the best seed of weight w (w = 9,10,11,12) among two categories: ordinary spaced seeds of weight w and subset seeds of weight w with two @. Ordinary spaced seeds were enumerated exhaustively up to a given span, and for each seed, the sensitivity was computed using the algorithmic approach of section 2 and the seed automaton construction of section 3. Each such computation took between 10 and 500ms on a Pentium IV 2.4GHz computer depending on the seed weight/span and the model used. In each experiment, the most sensitive seed found has been kept. The results are presented in Tables 2–5.

Table 2.

Best seeds and their sensitivity for probability transducer B

w	spaced seeds	Sens.	subset seeds, two @	Sens.
9	###___#_#_##_##	0.4183	###_#__#@#_@##	0.4443
10	##_##___##_#_###	0.2876	###_@#_@#_#_###	0.3077
11	###_###_#__#_###	0.1906	##@#__##_#_#_@###	0.2056
12	###_#_##_#__##_###	0.1375	##@#_#_##__#@_####	0.1481

Table 5.

Best seeds and their sensitivity for probability transducer NT

w	spaced seeds	Sens.	subset seeds, two @	Sens.
9	##_##_##____##_#	0.5253	##_@@_##____##_##	0.5420
10	##_##____##_##_##	0.4123	##_##____##_@@_##_#	0.4190
11	##_##____##_##_##_#	0.3112	##_##____##_@@_##_##	0.3219
12	##_##____##_##_##_##	0.2349	##_##____##_@@_##_##_#	0.2412

In all cases, subset seeds yield a better sensitivity than ordinary spaced seeds. The sensitivity increment varies up to 0.04 which is a notable increase. As shown in [19], the gain in using subset seeds increases substantially when the transition probability is greater than the inversion probability, which is very often the case in related genomes.

4.3. Comparative performance of spaced and subset seeds

We performed a series of whole genome comparisons in order to compare the performance of designed spaced and subset seeds. Eight complete bacterial genomes¹ have been processed against each other using the YASS software [19]. Each comparison was done twice: one with a spaced seed and another with a subset seed of the same weight.

The threshold E-value for the output alignments was set to 10, and for each comparison, the number of alignments with E-value smaller than 10⁻³ found by each seed, and the number of exclusive alignments were reported. By “exclusive alignment” we mean any alignment of E-value less than 10⁻³ that does not share a common part (do not overlap in both compared sequences) with any alignment found by another seed. To take into account a possible bias caused by splitting alignments into smaller ones (X-drop effect), we also computed the total length of exclusive alignments. Table 6 summarizes these experiments for weights 9 and 10 and the DT2 and NT probabilistic models. Each line corresponds to a seed given in Table 4 or Table 5, depending on the indicated probabilistic model. In all cases, best subset seeds detect from 1% to 8% more significant alignments compared to best spaced seeds of same weight.

Table 6.

Comparative test of subset seeds vs spaced seeds. Reported execution times (min: sec) were obtained on a Pentium IV 2.4GHz computer.

seed	time	#align	#ex. align	ex. align length
DT2, w = 9, spaced seed	15:14	19101	1583	130512
DT2, w = 9, subset seed, two @	14:01	20127	1686	141560
DT2, w = 10, spaced seed	8:45	18284	1105	10174
DT2, w = 10, subset seed, two @	8:27	18521	1351	12213
NT, w = 9, spaced seed	42:23	20490	1212	136049
NT, w = 9, subset seed, two @	41:58	21305	1497	150127
NT, w = 10, spaced seed	11:45	19750	942	85208
NT, w = 10, subset seed, two @	10:31	21652	1167	91240

Table 4.

Best seeds and their sensitivity for probability transducer DT2

w	spaced seeds	Sens.	subset seeds, two @	Sens.
9	#_##____##_##_##	0.5121	#_#@_##_@__##_##	0.5323
10	##_##_##____##_##	0.3847	##_@#_##__@_##_##	0.4011
11	##_##__#_#___#_##_##	0.2813	##_##_@#_#___#_#@_##	0.2931
12	##_##_##_#___#_##_##	0.1972	##_##_#@_##_@__##_##	0.2047

5. Discussion

We introduced a general framework for computing the seed sensitivity for various similarity search settings. The approach can be seen as a generalization of methods of [7, 5] in that it allows to obtain algorithms with the same worst-case complexity bounds as those proposed in these papers, but also allows to obtain efficient algorithms for new formulations of the seed sensitivity problem. This versatility is achieved by distinguishing and treating separately the three ingredients of the seed sensitivity problem: a set of target alignments, an associated probability distributions, and a seed model.

We then studied a new concept of subset seeds which represents an interesting compromise between the efficiency of spaced seeds and the flexibility of vector seeds. For this type of seeds, we defined an automaton with 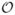(w2^r) states regardless of the size of the alignment alphabet, and showed that its transition table can be constructed in time 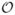(w2^r||). Projected to the case of spaced seeds, this construction gives the same worst-case bound as the Aho-Corasick automaton of [7], but results in a smaller number of states in practice. Different experiments we have done confirm the practical efficiency of the whole method, both at the level of computing sensitivity for designing good seeds, as well as using those seeds for DNA similarity search.

As far as the future work is concerned, it would be interesting to study the design of efficient spaced seeds for protein sequence search (see [6]), as well as to combine spaced seeds with other techniques such as seed families [17, 20, 16] or the group hit criterion [19].

Algorithm 1.

S_π computation

Table 3.

Best seeds and their sensitivity for probability transducer DT1

w	spaced seeds	Sens.	subset seeds, two @	Sens.
9	###___##_##_##	0.4350	##@___##_##_##@	0.4456
10	##_##____##_##_##	0.3106	##_##___@##_##@#	0.3173
11	##_##____##_##_###	0.2126	##@#@_##_##__###	0.2173
12	##_##____##_##_####	0.1418	##_@###__##_##@##	0.1477

A. Proof of Lemma 8

Let π = # –^r # be a spaced seed of span r + 2 and weight 2. We prove that the automaton S_π (see Lemma 6) is reduced, i.e.

1. all its non-final states are reachable from the initial state <∅,0 >;

2. any two non-final states q, q′ are non-equivalent, i.e. there is a word w = w(q, q′) such that exactly one of the states ψ(q, w), ψ(q′, w) is a final state.

Let q =< X, t> be a state of the automaton S_π, and let X = {x₁,…, x_k} and x₁ < · · · < x_k. Obviously, x_k + t < r + 2. Let s ∈ {0,1}* be an alignment word of length x_k such that for all i ∈ [1, x_k], s_i = 1 iff ∃j ∈ [1, k], i = x_k − x_j + 1. Note, that, π₁ = #, therefore 1 ∉ X and s_xk = 0. Finally, ψ (<φ,0 >, s · 1^t) = q.

Let q₁ =< X₁, t₁ > and q₂ =< X₂, t₂ > be non-final states of S_π. Let X₁ = {y₁,…, y_a}, X₂ = {z₁,…, z_b}, and y₁ < · · ·< y_a, z₁ < · · ·< z_b.

Assume that max{X₁} + t₁ > max{X₂} + t₂ and let d = (r + 2) − (max{X₁} + t₁). Obviously, ψ(q₁,1^d) is a final state, and ψ(q₂,1^d) is not. Now assume that max{X₁} + t₁ = max{X₂} + t₂. For a set X ⊆ {1,…, r + 1} and a number t, define a set X{t} by X{t} = {v + t|v ∈ X and v + t < r + 2}. Let g = max{v|(v + t₁ ∈ X₁ and v + t₂ ∉ X₂) or (v +t₂ ∈ X₂ and v +t₁ ∉ X₁)} and let d = r + 1 − g. Then ψ(q₁, 0^d · 1) is a final state and ψ (q₂,0^d · 1) is not or vice versa. This completes the proof.

B. Subset seed automaton

Let π be a subset seed of #-weight w and span s, and r = s − w be the number of non-# positions. We define a DFA S_π recognizing all words of 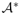matched by π (see definition of section 3.1). The transition table of S_π is stored in an array such that each element describes a state < X, t > of S_π. Now we define

1. how to compute the array index I nd(q) of a state q =< X, t >,

2. how to compute values ψ(q, a) given a state q and a letter a ∈ .

B.1. Encoding state indexes

We will need some notation. Let L = {l₁,…, l_r} be a set of all non-# positions in π (l₁ < l₂ <· · ·< l_r). For a subset X ⊆ L, let v(X) = v₁· · ·v_r ∈ {0,1}^r be a binary vector such that v_i = 1 iff l_i ∈ X. Let further n(X) be the integer corresponding to the binary representation v(X) (read from left to right):

$$n(X)=\sum _{j=1}^r{2}^{j-1}·v_j.$$

Define p(t) = max{p | l_p < m − t}. Informally, for a given non-final state < X, t >, X can only be a subset of {l₁,…, l_p(t)}. This implies that n(X) < 2^p(t). Then, the index of a given state {< X, t >} in the array is defined by

$$\mathit{Ind}(<X,t>)=n(X)+2^{p(t)}.$$

This implies that the worst-case size of the array is no more than w2^r (the proof is similar to the proof of Lemma 7).

B.2. Computing transition function ψ (q, a)

We compute values ψ(< X, t >, a) based on already computed values ψ (< X′, t >, a). Let q =< X, t > be a non-final and reachable state of S_π, where X = {l₁,…, l_k} with l₁ < l₂ · · ·< l_k and k ≤ r. Let X′ = X \ {l_k} = {l₁,…,l_k−1} and q′ =< X′, t >. Then the following lemma holds.

Lemma 10

If q =< X, t > is reachable, then q′ =< X′, t > is reachable and has been processed before.

Proof.

First prove that < X′, t > is reachable. If < X, t > is reachable, then < X, 0 > is reachable due to the definition of transition function for t > 0. Thus, one can find at least one sequence S ∈ ^l_k such that ∀i ∈ [1..r], l_i ∈ X iff π₁ · · ·π_li matches S_lk−li+1· · ·S_lk. For such a sequence S, one can find a word S′ = S_lk−lk−l+1 · · ·S_lk which reaches state < X′,0 >. To conclude, if there exists a word S · 1^t that reaches the state < X, t >, there also exists a word S′ · 1^t that reaches < X′, t >.

Note that as |S′ · 1^t| < |S · 1^t|, then a breadth-first computation of states of S_π always processes state < X′, t > before < X, t >.

Now we present how to compute values ψ(< X, t >, a) from values ψ (< X′, t >, a). This is done by Algorithm B.2 shown below, that we comment on now. Due to implementation choices, we represent a state q as triple q = 〈X, k_X, t〉, where k_X = max{i|l_i ∈ X}. Note first that if a = 1, the transition function ψ(q, a) can be computed in constant time due to its definition (part a. of Algorithm B.2). If a ≠ 1, we have to

1. retrieve the index of q′ given q = 〈X, k_X, t〉 (part c. of Algorithm B.2),

2. compute ψ(〈X, k_X, t〉, a ≠ 1) given ψ((X′, k_X′, t〉, a ≠ 1) value. (part d. of Algorithm B.2)

Note first that I nd(〈X, k_X, t〉) = I nd(〈X′, k_X′, t〉) − 2^k_x, which can be computed in constant time since k_X is explicitly stored in the current state.

Let

$$V_X(k,t,a\ne 1)=\{\begin{array}{ll}{l}_i\hfill & \text{if}{l}_i=l_k+t+1\text{and}a\text{matches}{\pi }_{l_i}\hfill \\ \varnothing \hfill & \text{otherwise}\hfill \end{array}$$

and

$$V_k(k,t,a\ne 1)=\{\begin{array}{ll}i\hfill & \text{if}{l}_i=l_k+t+1\text{and}a\text{matches}{\pi }_{l_i}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$

Tables V_X (k, t, a) and V_k (k, t, a) can be precomputed in time and space 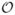(||·m²). Let ψ(〈X, k_X, t〉, a) = 〈Y, k_Y, 0〉 and ψ(〈X′,k_X′,t〉, a) = 〈Y′, k_Y′, 0〉. The set Y differs from Y′ at most with one element. This element can be computed in constant time using tables V_X, V_k. Namely Y = Y′ ∪ V_X (k_X, t, a) and k_Y = max(k_Y′, V_k(k_X, t, a)).

Note that a final situation arises when X = ∅. (part b. of Algorithm B.2). One also has to compute two tables U_X, U_k defined as:

$$\begin{array}{l}{U}_X(t,a\ne 1)=\cup \{x\mid x\le t+1\text{and}a\text{matches}{\pi }_x\}\\ U_k(t,a\ne 1)=\mathit{max}\{x\mid x\le t+1\text{and}a\text{matches}{\pi }_x\}\end{array}$$

Lemma 11

The transition function ψ(q, a) can be computed in constant time for every reachable state q and every a ∈ .

C. Training probability transducers

We selected 40 bacterial complete genomes from NCBI: NC_000117.fna, NC_000907.fna, NC_000909.fna, NC_000922.fna, NC_000962.fna, NC_001263.fna, NC_001318.fna, NC_002162.fna, NC_002488.fna, NC_002505.fna, NC_002516.fna, NC_002662.fna, NC_002678.fna, NC_002696.fna, NC_002737.fna, NC_002927.fna, NC_003037.fna, NC_003062.fna, NC_003112.fna, NC_003210.fna, NC_003295.fna, NC_003317.fna, NC_003454.fna, NC_003551.fna, NC_003869.fna, NC_003995.fna, NC_004113.fna, NC_004307.fna, NC_004342.fna, NC_004551.fna, NC_004631.fna, NC_004668.fna, NC_004757.fna, NC_005027.fna, NC_005061.fna, NC_005085.fna, NC_005125.fna, NC_005213.fna, NC_005303.fna, NC_005363.fna.

YASS [19] has been run on each pair of genomes to detect alignments with E-value at most 10⁻³. Resulting ungapped regions of length 64 or more have been used to train models DT1, DT2 and NT by the maximal likelihood criterion. Table 7 gives the ρ function of the probability transducer DT1, that specifies the probabilities of match (1), transition (h) and transversion (0) at each codon position.

Table 7.

Parameters of the DT1 model

a:	0	h	1
ρ(q0, a, q1)	0.2398	0.2945	0.4657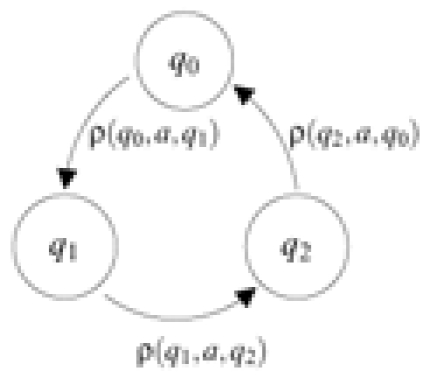
ρ(q1, a, q2)	0.1351	0.1526	0.7123
ρ(q2, a, q0)	0.1362	0.1489	0.7150

Table 8 specifies the probability of each codon instance a₁a₂a₃ ∈ , used to define the probability transducer DT2.

Table 8.

Probability of each codon instance specified by the DT2 model

a1\a2a3:	00	0h	01	h0	hh	h1	10	1h	11
0	0.01089	0.01329	0.01311	0.01107	0.00924	0.01144	0.01887	0.01946	0.03106
h	0.01022	0.00984	0.01093	0.00956	0.01025	0.01294	0.02155	0.02552	0.03983
1	0.02083	0.02158	0.02554	0.02537	0.02604	0.03776	0.11298	0.16165	0.27915

Finally, Table 9 specifies the probability transducer NT by specifying the four DT2 models together with transition probabilities between the initial states of each of these models.

Table 9.

Probabilities specified by the NT model

Pr (qi → qj)	j = 0	1	2	3
i = 0	0.9053	0.0947	0	0
1	0.1799	0.6963	0.1238	0
2	0	0.2131	0.6959	0.0910
3	0.0699	0.0413	0.1287	0.7601

a1\a2a3:		00	0h	01	h0	hh	h1	10	1h	11
q0:	0	0.01577	0.01742	0.01440	0.01511	0.01215	0.01135	0.02502	0.02353	0.02786
	h	0.01478	0.01365	0.01266	0.01348	0.01324	0.01346	0.02815	0.02981	0.03442
	1	0.02701	0.02838	0.02600	0.03429	0.03158	0.03406	0.12973	0.17461	0.17809
q1:	0	0.00962	0.01241	0.01501	0.00891	0.00753	0.01247	0.01791	0.01841	0.03530
	h	0.00818	0.00766	0.01115	0.00738	0.00952	0.01353	0.01828	0.02978	0.04405
	1	0.01946	0.01682	0.02344	0.02456	0.02668	0.03890	0.12113	0.18170	0.26020
q2:	0	0.00406	0.00692	0.00954	0.00501	0.00372	0.00841	0.01034	0.01129	0.03430
	h	0.00391	0.00396	0.00758	0.00364	0.00707	0.01473	0.01288	0.01975	0.05058
	1	0.01250	0.01627	0.02416	0.01419	0.02071	0.04427	0.10014	0.15311	0.39698
q3:	0	0.00302	0.00267	0.00560	0.00289	0.00249	0.00807	0.00740	0.00710	0.03195
	h	0.00297	0.00261	0.00355	0.00299	0.00271	0.00935	0.00924	0.01148	0.04296
	1	0.01035	0.01125	0.02204	0.00930	0.01289	0.04235	0.05304	0.08163	0.59810