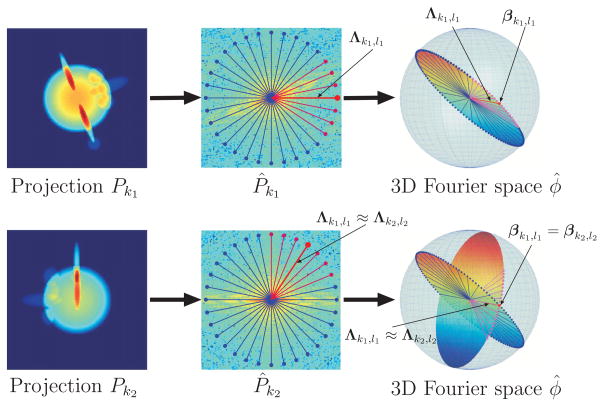
Figure 1.

Fourier projection-slice theorem and its induced geometry. The Fourier transform of each projection P̂_k corresponds to a planar slice through the three-dimensional Fourier transform φ̂ of the molecule. The Fourier transforms of any two projections P̂_k1 and P̂_k2 share a common line (Λ_k1,l1 and Λ_k2,l2), which is also a ray of the three-dimensional Fourier transform φ̂. Each Fourier ray Λ_k1,l1 can be mapped to its direction vector β_k1,l1. The direction vectors of the Fourier rays Λ_k1,l1 and Λ_k2,l2 that correspond to the common line between P_k1 and P_k2 must coincide, that is, β_k1,l1 = β_k2l2.