Approaches to analysis of handwriting as a task of coordinating a redundant motor system

Abstract

We consider problems of motor redundancy associated with handwriting using the framework of the uncontrolled manifold (UCM) hypothesis. Recent studies of finger coordination during force production tasks have demonstrated that the UCM-hypothesis provides a fruitful framework for analysis of multi-finger actions. In particular, it has been shown that during relatively fast force changes, finger force variance across trials is structured such that a time pattern of total moment produced by the fingers with respect to a point between the two most lateral fingers involved in the task is stabilized while the time pattern of total force may be destabilized. The findings of selective moment stabilization have been interpreted as being conditioned by the experience with everyday motor tasks that commonly pose more strict requirements to stabilization of total moment than to stabilization of total force. We discuss implications of these findings for certain features of handwriting seen in elderly, children, patients with neurological disorders, and forgers.

1. Problems of motor redundancy associated with handwriting

Writing with a regular pen on a horizontal piece of paper requires complex coordination of effectors that make contact with the pen as well as appropriate patterns of joint rotations and torques in more proximal joints. In this paper, we are going to consider writing as a task of producing a desired trajectory of the tip of the pen on a piece of paper. This definition does not distinguish between writing and drawing (cf. Adi-Japha & Freeman, 2001). Let us also make it clear upfront that, within this paper, we do not address the problems of the formation of the trajectory of the writing implement (cf. Viviani & Terzuolo, 1982; Morasso & Mussa Ivaldi, 1982; Plamondon, 1993; Wada & Kawato, 1995). We assume that those problems have already been solved by the central nervous system (CNS). Rather, we address the questions of the coordination of effectors that are expected to assure stable handwriting.

Let us consider basic features of the mechanics of the pen motion. Most commonly, the pen makes contacts with the hand at four sites, with a proximal portion of the hand (between the metacarpophalangeal, MCP joints of the thumb and the index finger or at the proximal phalange of the index finger), with the tips of the thumb, the index finger, and the lateral surface of the distal phalanx of the middle finger. At each contact site, a three-dimensional vector of force F can be applied to the pen. Note that contact sites are soft and, therefore, they do not represent points but rather areas. Because of the non-point contact, a moment M is also produced with respect to a nominal point of contact. If the pen does not stick to the skin the moment vector is normal to the surface of contact. The moment M is due to (a) the moment of force F and (b) a force couple (free moment) acting at the area of contact. We are going to assume that the basic grip of the pen is not changing in the process of writing, i.e. the positions of the three digits are fixed, while the site of the more proximal contact can change because of the sliding motion of the pen. Except in some special examples, we are also going to assume that the position of the paper does not change with respect to an external reference frame, e.g., with respect to the table or with respect to the trunk of the person.

In three dimensions, any set of forces and moments acting on a rigid body can be uniquely represented by a wrench, i.e. a combination of a force vector and a moment vector both acting along the same or parallel lines (Zatsiorsky, 2002). Each site of contact acting on a hand-held object (e.g., the fingertips and the proximal contact site acting on a writing implement) produces a wrench acting on the object along a certain axis. Four individual wrenches always form a redundant set since they cannot act along four orthogonal directions. In other words, a force/moment generated at one site can be counterbalanced by another force/moment along the same wrench axis. Hence, producing an adequate grip of the pen in the process of handwriting is a typical example of controlling a redundant system, when analyzed at the level of the production of forces and moments at each contact site.

Hollerbach (1981) suggested considering handwriting as a superposition of two movements, a translation of the pen and an oscillatory motion of the tip of the pen (see also Singer & Tishby (1994) who considered handwriting as a modulation of a simple cycloidal pen motion, described by two coupled oscillations, with a constant linear drift along the line of the writing). The motion of the tip of the pen gets contributions from at least two components: First, there is motion of the hand with respect to the external reference frame and, second, there is motion of the pen with respect to the hand. The relative contribution of these two motions to the kinematics of the tip of the pen can vary. For example, one can write with the tip of the extended index finger (or with a pen tightly taped to the index finger) when apparently the whole writing pattern is produced by the first component. On the other hand, one can write without moving the hand, for example on moving paper, when the second component dominates. We assume that during natural handwriting, both components contribute to the trajectory of the pen on the paper (cf. Lacquaniti, Ferrigno, Pedotti, Soechting, & Terzuolo, 1987; Meulenbroek, Thomassen, van Lieshout, & Swinnen, 1998; Dounskaia, Van Gemmert, & Stelmach, 2000).

Bernstein (1967) considered the task of producing a required trajectory of the fingertip in space and used it to illustrate his famous problem of motor redundancy (the Bernstein problem – Turvey, 1990; Latash, 1996). Three major joints of the human arm, wrist, elbow, and shoulder, have the total of seven major axes of rotation. This set of seven variables is redundant in a sense that no unique combination of joint angles can be computed based on a required instantaneous position of the endpoint in space, which can apparently be defined by only three coordinates. Hence, producing an adequate hand motion in the process of handwriting is a typical example of control of a redundant system, when analyzed at the level of coordinated joint angle rotations (cf. the problem of inverse kinematics, Mussa Ivaldi, Morasso, & Zaccaria, 1989; Zatsiorsky, 1999).

Handwriting has its own specificity. All multi-finger grasps combine serial and parallel mechanisms. Individual digits can be viewed as serial mechanisms. They are redundant (under-constrained) in kinematics and over-constrained in statics. In contrast, several fingers grasping a rigid object represent a parallel mechanism that is over-constrained in kinematics, i.e. movement of one finger induces movement of the other fingers, and is under-constrained (redundant) in statics (cf. Burstedt, Flanagan, & Johansson, 1999).

Three variables, the distance from the tip of the pen to the proximal contact and two angles vary in a coordinated fashion to preserve the contact of the tip of the pen with the paper. Motion of the pen with respect to the hand results from motions in the MCP and interphalangeal joints of the three involved digits. These motions, however, need to be coordinated to preserve the grip configuration and are constrained by the geometry of the hand. Under these conditions, the system does not seem to possess redundancy: We challenge the reader to try to move the tip of the pen back and forth over a piece of paper without changing the lateral tilt of the pen “in different ways”. However, because of the redundancy in the first component, the overall kinematic system involved in handwriting is redundant.

We can conclude, therefore, that the redundancy during handwriting comes from three sources: (a) individual wrenches and their combinations can cancel each other out, i.e. a force/moment generated by one digit can be counterbalanced by another force/moment along the same wrench axis, (b) three digits plus an additional contact are redundant for a task that can be performed by a smaller number of digits (contacts), and (c) the number of kinematic DOF of the contacting digits is redundant for the task that has not more than three DOF.

2. Approaches to ill-posed problems

Ill-posed problems emerge commonly in movement studies. The best studied ones are the problem of inverse kinematics and the problem of inverse dynamics (Atkeon, 1989; Mussa Ivaldi et al., 1989). The former asks a question how to define a pattern of joint rotations for a given trajectory of the endpoint of a multi-joint limb. The latter deals with joint torques that produce a certain endpoint motion. Such problems emerge also at other levels of description of the neuromotor system including both serial and parallel manipulators. Examples include: (1) define forces of individual muscles crossing a joint that would produce a required value of joint torque; (2) define forces produced by, individual fingers that would produce a required total force of a hand-held object; or (3) define which motor units should be recruited and at which frequencies to produce a required level of muscle activation. Commonly, such problems have been addressed using a variety of optimization criteria (for reviews see Seif-Naraghi & Winters, 1990; Latash, 1993; Rosenbaum, Loukopoulos, Meulenbroek, Vaughan, & Engelbrecht, 1995; Prilutsky, 2000; Prilutsky & Zatsiorsky, 2002).

Bernstein formulated the main problem of motor control as “the elimination of redundant degrees-of-freedom”. Following his traditions, many studies addressed various ill-posed problems trying to find unique solutions with the help of different computational approaches. Neuromotor structures underlying such solutions have commonly been addressed as “synergies”.

Gelfand and Tsetlin, in early 1960s, tried to develop a stringent theory of synergies (Gelfand & Tsetlin, 1966). They considered a hierarchical system with at least two levels, a controller, and a large set of elements united into what they called a “structural unit”. Later, ideas of Gelfand and Tsetlin have been developed into a principle of abundance, according to which many more elements than necessary participate in the activity of a structural unit with respect to each task such that apparently redundant degrees-of-freedom are not eliminated but used to stabilize important performance variables (Gelfand & Latash, 1998). The notion of “structural unit” is equivalent to the contemporary usage of the notion of “synergy”, and we will use these as synonyms.

A synergy may be characterized by two features. First, there are particular preferred relations among outputs of each element, which are seen in the averages over several realizations of a task. Such relations have been described for a variety of tasks including vertical posture, locomotion, reaching, finger force production, etc. (Smith, Hoy, Koshland, Phillips, & Zernicke, 1985; Macpherson, Rushmer, & Dunbar, 1986; Desmurget et al., 1995; Wang & Stelmach, 1998; Santello & Soechting, 2000; Pelz, Hayhoe, & Loeber, 2001). If we assume, for simplicity, that the elements contribute in an additive way to a common functional output, this feature favors positive correlations among outputs of individual elements such that the “sharing pattern” (e.g., Li, Latash, & Zatsiorsky, 1998a) is preserved. Principal component analysis has been previously used to identify such sharing patterns over a time realization of an action or over a range of task parameters, assuming that phase relations among the outputs of the elements are stable (Alexandrov, Frolov, & Massion, 1998; Sanger, 2000).

Second, if the output of an element in a particular trial is different from its average (expected) output, the outputs of other elements may change such that the overall functional output of the structural unit is preserved. Such relations may be expected to be reflected in certain regularities of variability patterns over a number of task realizations, but not in averages.

These two features of synergies are in a seeming competition. Imagine that a person is asked to press with two hands and produce a ramp pattern of total force increasing from zero to some high level of force. Imagine also that the person, on average, produces 60% of the total force with the right hand. If one analyzes individual force changes over such a ramp within one trial, a strong positive correlation will be found, i.e. a stable sharing pattern (Li et al., 1998a). Imagine now that the person performs this task many times. In one trial, halfway up, the right hand produced a spontaneous error (its force becomes too high). What would be the deviation of the force of the left hand from its average preferred value? The first feature of synergies (sharing pattern) predicts that it will be proportionally higher such that its share stays at 40%, while the second feature (error compensation) predicts that it will be lower to keep the total force closer to its required instantaneous level.

We would like to suggest that the second feature, i.e. error compensation among elements, is salient for biological synergies while the first one is not. Imagine now that a person presses with the four prongs of a fork on four force sensors. The total force changes to produce a similar ramp as in the previous example. There will be a strong positive correlation among the forces produced by individual prongs, i.e. a stable sharing pattern. However, in no situation will error compensation occur: If in one trial, a prong produces an error, all other prongs will produce errors in the same direction such that the error in the total force will not be reduced but amplified. A fork is not a biological object and we would like to suggest that the notion of synergy should not be applied to it. Since we are interested primarily in neural control of synergies, let us focus on recent attempts to analyze phenomena of error compensation during natural motor tasks.

3. Multi-finger force production as an example of a synergy

The human hand is an exceptional model for the analysis of the coordination mechanisms of multi-element systems. For example, one can view each digit of the hand as a force (and possibly moment) generator and ask the following question: How is the total force and/or total moment shared among the digits in prehension and manipulation of objects? A recent series of studies (Li et al., 1998a; Li, Latash, Newell, & Zatsiorsky, 1998b; Latash, Gelfand, Li, & Zatsiorsky, 1998a; Latash, Li, & Zatsiorsky, 1998b; Zatsiorsky, Li, & Latash, 1998, 2000) of finger coordination during force production tasks has allowed identification of a number of characteristics of this coordination that potentially reflect both the peripheral design of the hand musculature and its central neural coordination: (1) Sharing (total force is shared among the fingers in a stable way over a wide range of total force); (2) Deficit (peak force produced by a finger in a multi-finger task is smaller than its peak force in a similar single-finger task, see also Ohtsuki, 1981 and Kinoshita, Murase, & Bandou, 1996); and (3) Enslaving (voluntary force production by a finger leads to involuntary force production by other fingers of the hand, see also Kilbreath & Gandevia, 1994). A constraint principle termed the principle of minimization of secondary moments has been introduced that limits possible sharing patterns during force production tasks.

Physiological mechanisms underlying finger interaction are mostly unknown. Partly, these phenomena may be due to shared extrinsic hand muscles and passive connections (Leijnse et al., 1993; Kilbreath & Gandevia, 1994). However, many recent studies (reviewed in Lemon, 1993; Schieber, 1999) emphasize the role of neural factors in finger interaction. In particular, they have shown both convergence of output from large, overlapping cortical territories onto single muscles, and divergence of output from any given cortical site to multiple muscles. Extensive horizontal interconnections among neurons throughout the M1 hand area have been described, and finger movement has been associated with activation throughout the M1 hand area.

In earlier studies by our group, there were signs that fingers were united into synergies (or structural units) during force production tasks. In particular, in one study (Li et al., 1998a), subjects were asked to produce ramp forces from zero to a level close to their maximal force. They performed this task several times, and then variances of the total force and of individual finger forces were computed at the level close to peak force. In all subjects, the sum of the variances of individual finger forces was higher than the variance of the total force suggesting that fingers were not independent force generators. In another study (Latash et al., 1998b), subjects were asked to produce constant force with three fingers pressing in parallel, the index, the middle, and the ring finger. Then, they were asked to tap with one finger. During the first tap, the “tapping finger” lost contact with the sensor and stopped producing force. The other two fingers changed their forces out-of-phase with the tapping finger such that they compensated for close to 100% of the lost force.

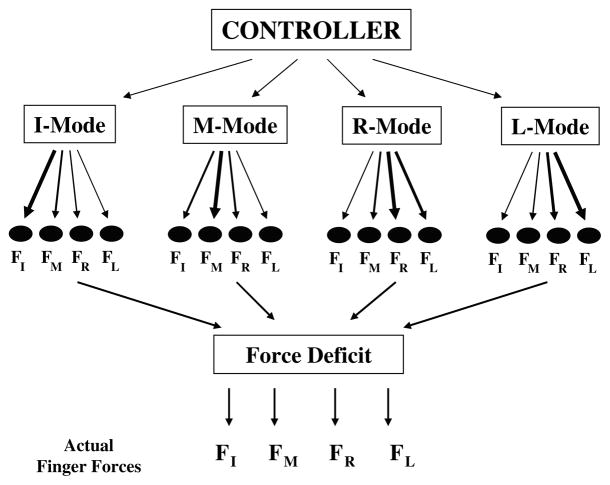
During force production (and other) tasks, fingers of the hand do not behave as independent force generators (Hager-Ross & Schieber, 2000). An attempt to change the total force by pressing harder with one finger invariably leads to changes in the forces produced by all the fingers. This phenomenon of enslaving has been recently expressed as a matrix equation (Latash, Scholz, Danion, & Schöner, 2001; Danion et al., in press):

$$\mathbf{F}=k\ast \text{ENSL}\ast \mathbf{M},$$ (1)

where F is a vector of individual finger forces and M is a vector of commands to individual fingers (Fig. 1). Each command represents a variable that will be addressed as a “force mode”. For example, a command to press with the index finger at 50% of its maximal force corresponds to a value of the index finger mode of 0.5(M_I = 0.5); it will be associated with changes in the forces of all four fingers. The columns of the ENSL matrix contain derivatives of individual finger forces to total force when only one finger is intended to produce force. A coefficient k reflects an attenuating factor responsible for the phenomenon of force deficit. Experimentally, columns of the ENSL matrix have been obtained by asking a subject to produce a slowly increasing ramp force while following a template and pressing on a force sensor with only one finger (Latash et al., 2001; Scholz, Danion, Latash, & Schöner, 2002). All other fingers remained on force sensors, and the subject was not allowed to lift them of the sensors. The subject was instructed not to pay attention to possible force generation by these fingers (“slave fingers”) as long as the explicitly involved finger (the “master finger”) produced the required force profile. In such tests, all slave fingers produced forces that increased nearly linearly with the force produced by the master finger. Changes in individual finger forces were measured within a comfortable force range and divided by the change in the total force. This procedure resulted in four coefficients describing changes in the forces produced by all four fingers in response to a command to press with only one finger. The tests were repeated for each finger acting as the master finger, producing a 4 × 4 matrix.

Fig. 1.

An illustration of the notion of force modes. The controller specifies coefficients for four independent variables, force modes, coresponding to the degrees of intended involvement of individual fingers. Actual finger forces are defined by the summed contribution of the modes attenuated by a factor responsible for force deficit.

This approach and the experimental procedures are based on a hypothesis that the CNS manipulates four control variables, the force modes, corresponding to intended involvement of individual fingers in a multi-finger task. For example, if one wants to press as strongly as possible with the index and middle fingers only, the vector of force modes would be [1,1,0,0]. If one wants to press with the index finger at 50% of its maximal force and with the little finger at 25% of the maximal force, the vector of force modes would be [0.5,0,0,0.25]. Fig. 1 illustrates this approach. Note that finger forces corresponding to each mode sum up with an “attenuating factor” responsible for the phenomenon of force deficit.

To analyze neural coordination of individual fingers in multi-finger tasks, one needs to perform analysis in the space of force modes that presumably represent four variables that are manipulated independently by the controller. Because of the enslaving, finger forces are not independent variables in a sense that an attempt by the controller to modify the force of a finger is accompanied by changes in the forces of other fingers. Analysis using force modes was done in a few recent studies.

4. The uncontrolled manifold hypothesis

A new quantitative approach to the problem of coordinating many elements has recently been suggested (Schöner, 1995; Scholz & Schöner, 1999; Scholz, Schöner, & Latash, 2000, 2001, 2002; Latash et al., 2001, 2002) that shares much in common with the traditions of Gelfand and Tsetlin and is in accordance with the principle of abundance. According to this approach, setting a task may be associated with selecting a set of performance variables that are selectively stabilized with respect to possible perturbations (internally and externally generated). In other words, a structural unit is created with an interaction among its elements organized in such a way that the selected performance variable shows less variance across different realizations of the task than other performance variables.

This process may be viewed as selecting a lower-dimensional subspace (a manifold) within the state space of elements for each instant of time. This manifold is such that changes in elements states within the manifold do not change a certain desired instantaneous value of the selected performance variable. One may say that the elements are less controlled within the manifold than outside it in a sense that each of them can show higher variability of its output within the manifold. Hence, the manifold has been termed “uncontrolled manifold (UCM)” and the hypothesis has been addressed as the “UCM-hypothesis”.

Consider, as an example, the task of producing a total force of F₀ with two force-generating elements (e.g., hands) pressing on two force sensors. Total force is the performance variable of the system. The state space of this system is two-dimensional, a plane whose points correspond to combinations of values of two forces (F₁ and F₂) produced by the hands. One can associate this task with an equation F₁ + F₂ = F₀ corresponding to a straight line with a negative slope on the force–force plane. The line is a UCM for the task. Imagine now that the subject performs the task many times and individual hand forces are measured. If the two hands work as a structural unit, points on the force–force plane corresponding to individual attempts are expected to form a cloud elongated along the UCM.

A priori, a multi-element system can function without selecting an UCM but simply by stabilizing a state of the system equally in all directions within the state space. The UCM-hypothesis suggests, however, that this is not how control of voluntary movements is organized.

Gelfand and Tsetlin (1966) introduced the principle of minimal interaction, which predicts that modifications of the states of individual elements of a system will occur to offset perturbations to the states of other elements so that successful execution of a functionally important task is not jeopardized. If one associates high stability of a selected performance variable with successful execution of a task, then the UCM-hypothesis predicts a range of equivalent solutions to multi-element coordination consistent with the principle of minimal interaction.

5. Recent studies of finger coordination using the UCM-hypothesis

Recently, we have performed a series of studies of finger coordination using the framework of the UCM-hypothesis (Latash et al., 2001; Scholz et al., 2002). All the experiments shared particular methodological features. Subjects, first, were asked to produce maximal forces by each finger and by subsets of fingers pressing together. These data were later used for setting up other tasks and for normalization purposes. Then, subjects were asked to press with only one finger to match the force profile indicated by a template displayed on a computer screen. Other fingers also produced forces due to enslaving, and all the forces were recorded. The purpose of this procedure was to assess force modes, i.e. combinations of finger forces seen during attempts to use only one finger at a time (cf. Eq. (1)). This was followed by the main task, which was performed several times to ensure that at least 20 realizations were available for analysis. The main tasks could involve oscillatory force production with two, three, or all four fingers pressing in parallel. We also asked subjects to produce similar force patterns in conditions of instability, i.e. when the plate with the force sensors was placed on a narrow (4 mm wide) supporting surface. In these conditions, the explicit task requirement to produce a pattern of force was accompanied with an implicit task of not losing balance, i.e. stabilizing the total moment produced by all fingers with respect to the middle of the supporting surface. In other experiments, subjects were asked to produce discrete ramp profiles of total force as well as cyclic forces at a fast rate or at a slow rate.

The range of force changes was always kept from 5% to 25% of the maximal force that could be produced by the explicitly involved fingers. We also manipulated the visual feedback. The subjects either had an explicit template on the screen that they were supposed to follow with the total force signal or, alternatively, they were shown only the required levels of peaks and troughs of the total force, without connecting lines.

All attempts at a particular task were aligned, and the variance of the finger modes was computed across trials at each 10% of the task duration. This variance was later partitioned into two components, compensated variance (V_COMP) and un-compensated variance (V_UN) with respect to a particular control hypothesis, i.e. a hypothesis that the CNS tried to stabilize a particular performance variable. V_COMP represented a component of total variance within the UCM computed for a particular control hypothesis, while V_UN represented a component of the total variance orthogonal to the UCM. To review in the present context, the UCM is a manifold within the state space of finger modes, within which changes in modes do not affect the value of a relevant hypothesized performance variable. Both V_COMP and V_UN were normalized by the number of involved dimensions (DOFs). According to the UCM-hypothesis, if a particular performance variable is selectively stabilized by a multifinger synergy, V_COMP should be larger than V_UN.

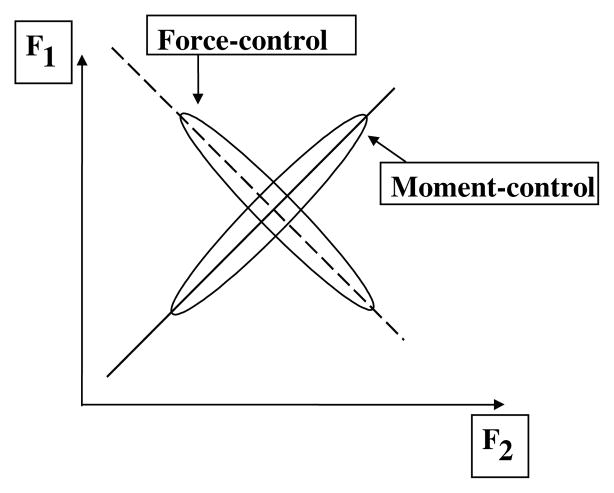
Two control hypotheses were compared: First, that the CNS tried to stabilize an average value of total force (“force-control”) and, second, that the CNS tried to stabilize the average value of the total moment (“moment-control”) produced by the fingers with respect to a midpoint between the two most lateral involved fingers. Fig. 2 illustrates the two hypotheses and the partition of the variance into V_COMP and V_UN for a task when only two fingers produce force. The oblique line with a negative slope shows a UCM for the force-control hypothesis; if individual finger force data are confined mostly to this line (ellipses in Fig. 2 show hypothetical data distributions across trials), one can conclude that their total force is selectively stabilized. The oblique line with a positive slope shows a UCM for the moment-control hypothesis. Note that, when only two fingers produce force, force-control and moment-control requirements are incompatible since the former requires a negative covariation between finger forces while the latter requires a positive covariation.

Fig. 2.

An illustration of two possible data distributions (shown by ellipses) in an experiment when the subject is instructed to produce a certain level of total force by pressing with two effectors. If the variabilities of forces (F₁ and F₂) produced by each eFector are coordinated to stabilize the total force, the data distributions are expected to show an ellipse elongated along a line with a negative slope (dashed). If the variabilities of the two forces are coordinated to stabilize the total moment with respect to a midpoint between the points of force application, the data distributions are expected to show an ellipse elongated along a line with a positive slope (solid). The two lines correspond to the UCMs for the total force-control hypothesis and moment-control hypothesis, respectively.

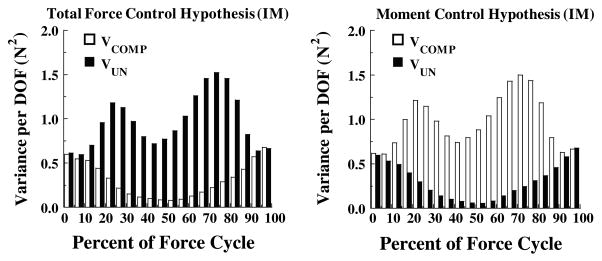
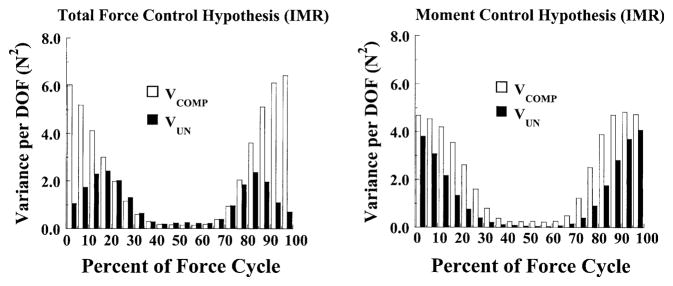
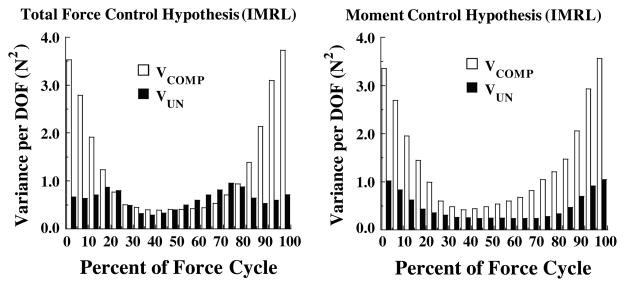
The first studies that looked only at oscillatory movements performed at a high rate (about 2 Hz) produced unexpected results. Although the subjects were explicitly asked to control total force produced by the required fingers, they tended to show strong moment stabilization and force destabilization, particularly at low to moderate forces. In particular, when only two fingers were involved, moment stabilization and force destabilization were seen over much of the force cycle (Fig. 3). When three fingers take part in such a task, theoretically, they can stabilize both total force and total moment: The forces of the two “lateral” fingers should be positively correlated while the third (“middle”) finger force should be negatively correlated with the sum of the forces of the two “lateral” fingers. This was found at the higher forces: both total force and moment were stabilized there (Fig. 4). However, the control system of the subjects did not take advantage of this opportunity throughout the force cycle. When the third finger was added, the total force was destabilized over much of the force cycle, while moment was stabilized over the whole force cycle. These results were observed in both stable and unstable conditions. Only when four fingers pressed in parallel were the subjects able to avoid force destabilization. Still, total force was stabilized over less than half of the cycle, while moment was stabilized over the whole cycle duration (Fig. 5).

Fig. 3.

An illustration of the two variance components computed over a series of force cycles for a representative subject who performed the task of cyclic force production with two fingers (index and middle, IM). Force cycles were aligned with respect to the peak forces. Open bars – V_COMP; filled bars – V_UN. Note that the total moment was stabilized over most of the force cycle (V_COMP > V_UN for moment-control) while total force was destabilized over most of the cycle (V_COMP < V_UN for force-control).

Fig. 4.

An illustration of the two variance components computed over a series of force cycles for a representative subject who performed the task of cyclic force production with three fingers (index, middle, and ring, IMR). Force cycles were aligned with respect to the peak forces. Open bars – V_COMP; filled bars – V_UN. Note that the total moment was stabilized (V_COMP > V_UN) over the whole force cycle, while total force was destabilized (V_COMP < V_UN) over much of the cycle.

Fig. 5.

An illustration of the two variance components computed over a series of force cycles for a representative subject who performed the task of cyclic force production with all four fingers (index, middle, ring, and little). Force cycles were aligned with respect to the peak forces. Open bars – V_COMP; filled bars –V_UN. Note that the total moment was stabilized (V_COMP > V_UN) over the whole force cycle, while total force was stabilized only at relatively high forces (V_COMP > V_UN) while V_COMP ≈ V_UN over the rest of the force cycle.

We have interpreted these findings as being biased by the lifetime experience which requires, in most everyday grasping and manipulation tasks, precise stabilization of total moment produced by the fingers with respect to the point of thumb contact, while total force only needs to be above the slipping threshold and below the crushing level. For example, during drinking from a glass, the grip force should only be sufficient to prevent the glass from slipping out of the hand. The total moment, however, should be precisely controlled to avoid spilling the contents of the glass.

In a more recent study, both discrete (ramp) and oscillatory two-finger force production tasks were studied. Only minor effects of task (discrete or oscillatory) and of template (with or without) were seen on the variance profiles. In contrast, the rate of force production had major effects on the two variance components. V_UN showed a strong relation to the rate of force production and only weak dependence on the magnitude of force. In contrast, V_COMP showed minimal effects of the rate force of production and strong effects of the force magnitude (Fig. 6). We used a model of motor variability proposed by Simon Gutman/Goodman and his colleagues (Gutman & Gottlieb, 1992; Gutman, Latash, Gottlieb, & Almeida, 1993) to analyze the role of two sources of motor errors, one related to an imprecise setting of a parameter A related to planned movement amplitude and the other related to an imprecise setting of a parameters τ related to movement time. Within this model, most of the A-related variance gets into V_COMP, i.e. it has little effect on the total force variance. In contrast, most of the τ-related variance gets into V_UN, which, by definition, affects the variance of the main performance variable, i.e. the total force.

Fig. 6.

Two components of variance are shown for a representative subject who performed the task of quick ramp force changes over 300 ms by pressing with two fingers (index and middle, IM). V_COMP is illustrated in the left graph (solid line) together with the average profile of the force (dashed line). V_UN is illustrated in the right graph (solid line) together with the average profile of the rate of force changes (dashed line). Note the similarities of the solid and dashed curves shown in both graphs.

These results may be interpreted as demonstrating a limitation in the ability of the CNS to organize a two-finger synergy to compensate for errors in the timing of force-related control signals by an interaction at the synergy level, which defines force profiles of individual fingers. Apparently, error correction between the outputs of the two fingers involves time delays that may be too long to allow an efficient stabilization of the total force during fast rates of the force production. In contrast, inter-compensation of errors related to imprecise setting of force magnitudes was rather efficient such that much of this variance got into V_COMP and was not reflected in the variance of the total force (or in V_UN). While arguments about the higher ecological value of moment stabilization may be correct, these results point at another major factor that defines which of the two major kinetic variables, force or moment, is stabilized. This factor is related to the rate of force development.

6. Implications of finger coordination studies for handwriting

The UCM-hypothesis offers a set of tools to address several crucial issues regarding the organization of motor synergies. In particular, it allows: (1) Analysis of whether a particular performance variable is selectively stabilized; (2) Comparisons of the relative degree of stabilization of different performance variables of a multi-element system; (3) Analysis of changes in the stabilization of performance variables with practice (cf. Domkin, Laczko, Jaric, Johansson, & Latash, 2002); and (4) Comparisons among hypotheses about stabilization of different performance variables in special populations. The two last issues can potentially be directly applicable to studies of handwriting.

Let us consider two findings of the reviewed studies that may be particularly relevant. First, there is preferential stabilization of moment by a set of fingers during relatively fast force production tasks, as well as in tasks that combined an explicit requirement to produce a required fast pattern of total force with an implicit requirement to keep total moment within a narrow acceptable range (in unstable conditions – Latash et al., 2001). Second, multi-finger synergies seem to function better with respect to an explicit task of total force-control during slow rates of force change. In other words, during the production of quickly changing forces, the CNS tends to use a “fork strategy”, i.e. keeping a constant sharing pattern among the fingers, which leads to predominantly positive covariations among individual finger forces and to stabilization of moment with respect to a point located between the most “lateral” fingers.

Handwriting is a relatively fast task involving frequencies of the motion of the tip of the pen over 2 Hz (Kunesch, Binkofski, & Freund, 1989; Siebner et al., 2001). According to our latest results, at such frequencies, a “fork strategy” is likely to dominate. Let us assume that the subject is writing with only three points of contact between the hand and the pen, at the thumb, at the index finger, and at the middle finger. Then, the oscillating motion of the tip of the pen may be viewed as produced by time varying moment applied by the two fingers with respect to the thumb contact (this is a major simplification), which is in-between the sites of finger contact. A “fork strategy” would be efficient in stabilizing a time pattern of this moment. Therefore, if a person has a motor program responsible for his or her individual natural handwriting, the “fork strategy” will effectively stabilize it against possible perturbations, both intrinsic and extrinsic. (We use the heavily abused term “motor program” simply to reflect a combination of neural signals, somewhere high within the neuro-motor hierarchy, which accompany a well learned motor action.)

Let us now consider what is likely to happen during slow handwriting. Our results suggest that total force applied by the two fingers is likely to become stabilized while the moment may become destabilized (cf. Fig. 2). This will require constant monitoring of the action and its explicit corrections in cases of spontaneously occurring errors. In a way, handwriting will turn into a drawing pattern resembling handwriting. One of the authors of this paper tried to “forge” his own signature by writing at a very slow pace. The results were miserable, although certain features of the natural signature were present. In particular, lines became wobbly and some features of the natural signature disappeared while other features became exaggerated. This example supports earlier observations (similarly pilot ones – see Latash, 1993) that another person is equally able to forge one’s own handwriting if both persons are writing slowly and using “unusual effectors”, with the pen in the non-dominant hand, tied to a foot, or gripped between the teeth.

One can tentatively conclude that natural handwriting depends crucially on the stability of one’s individual multi-digit synergies. Such stability can be assured only for actions that require force production patterns at a relatively high rate. If such synergies are not available or lost, as in forgers, in very young children, and in patients with certain neurological diseases, one can only try to compensate for the missing synergies. Different means can be used for such an adaptive compensation.

In particular, one can view micrographia and bradykinesia in handwriting typically seen in patients with Parkinson’s disease (Van Gemmert, Teulings, Contreras-Vidal, & Stelmach, 1999), but also described for patients with Huntington disease (Phillips, Bradshaw, Chiu, & Bradshaw, 1994) and for healthy elderly (Walton, 1997), as consequences of the impaired interaction among digits leading to poor moment stabilization necessary for stability of the output of the handwriting synergy. Slowness may be beneficial in two aspects. First, slower movements are typically associated with smaller force changes (Gottlieb, Corcos, & Agarwal, 1989); on the other hand, smaller force changes are associated with smaller force variability characteristics (Newell, Carlton, & Hancock, 1984). Hence, one can expect smaller deviations of individual digit forces from an optimal pattern, i.e. smaller intrinsic perturbations against which the synergy needs to be stabilized. Besides, slower movements allow more time for corrections of motor patterns based on sensory feedback. Micrographia is associated with smaller amplitude of the motion of the writing implement, and as such is also associated with smaller force changes.

Another way of stabilizing a motor pattern in the absence of an adequate synergy is to use excessive co-contraction of opposing muscles such that joint mechanical properties are changed, including, in particular, an increase in the apparent stiFness (Van Den Heuvel, Van Galen, Teulings, & Van Gemmert, 1998). Co-contraction is arguably the most commonly seen change in motor patterns across many tasks and subpopulations including children, elderly, and patients with various neurological, peripheral, and cognitive impairments (Gowland, deBruin, Basmajian, Plews, & Burcea, 1992; Hadders-Algra, Van Eykern, Klip-Van den Nieuwendijk, & Prechtl, 1992; Aruin, Almeida, & Latash, 1996; Burnett, Laidlaw, & Enoka, 2000; Canning, Ada, & O’Dwyer, 2000; Newham & Hsiao, 2001; Schmitz, Martin, & Assaiante, 2002). It has also been described for people who try to forge handwriting of another person (Van Galen & Van Gemmert, 1996; Van Gemmert & Van Galen, 1996).

To substantiate these speculations one needs to analyze patterns of forces and moments applied by individual digits on the implement during handwriting. Presently, the UCM-hypothesis offers a framework for such an analysis, and the only limitation is technological: instrumenting a “pen” with a set of miniature six-dimensional force sensors that would provide information on the mechanical interaction between the pen and the hand.

We would like to summarize the paper with the following messages that we cannot prove but about which we feel very strongly:

1. Any motor skill, including handwriting, is not in a “motor program” (whatever it is) but in mutual relations among elements participating in the motor activity which stabilize important performance variables;

2. Learning a synergy is much harder than learning a motor pattern. However, the benefits are much larger; and

3. Forging a synergy is much harder than forging a signature.