Compensations in response to real-time formant perturbations of different magnitudes

Abstract

Previous auditory perturbation studies have demonstrated that talkers spontaneously compensate for real-time formant-shifts by altering formant production in a manner opposite to the perturbation. Here, two experiments were conducted to examine the effect of amplitude of perturbation on the compensatory behavior for the vowel ∕ε∕. In the first experiment, 20 male talkers received three step-changes in acoustic feedback: F1 was increased by 50, 100, and 200 Hz, while F2 was simultaneously decreased by 75, 125, and 250 Hz. In the second experiment, 21 male talkers received acoustic feedback in which the shifts in F1 and F2 were incremented by +4 and −5 Hz on each utterance to a maximum of +350 and −450 Hz, respectively. In both experiments, talkers altered production of F1 and F2 in a manner opposite to that of the formant-shift perturbation. Compensation was approximately 25%–30% of the perturbation magnitude for shifts in F1 and F2 up to 200 and 250 Hz, respectively. As larger shifts were applied, compensation reached a plateau and then decreased. The similarity of results across experiments suggests that the compensatory response is dependent on the perturbation magnitude but not on the rate at which the perturbation is introduced.

INTRODUCTION

Auditory feedback plays an essential role in speech-motor control. Clinical studies have identified deficits in speech acquisition when hearing is impaired (Oller and Eilers, 1988) as well as deterioration of speech following post-lingual hearing loss (Cowie and Douglas-Cowie, 1992). Recent experimental work using perturbation techniques indicates that many aspects of speech—loudness control (Bauer et al., 2006), timing (Kalveram and Jäncke, 1989), pitch (Burnett et al., 1998), and formant frequency (Houde and Jordan, 1998)—are influenced by changes in the sound of the talker’s voice. When feedback is unexpectedly changed, subjects alter their productions so as to compensate for the changes in the way they hear their own voice. These studies suggest that auditory feedback is part of a control system that actively influences the accuracy of articulator movement.

The nature of this control system for speech and other movements is not completely understood. It is generally believed that the controller must incorporate both feedforward (predictive) behavior and more direct feedback mechanisms (Wolpert and Kawato, 1998) and that both aspects of the controller are adaptive. The adaptive feedforward portion of this controller uses sensory information to learn a detailed representation or “internal model” of the articulator system and its environment and to improve the accuracy of the prediction through evaluating feedback errors (Kawato, 1989). The adaptive feedback portion of the controller is involved in rapid, immediate response to changes in sensory information (Churchland and Lisberger, 2009).

In speech production, auditory feedback plays a complex role in controlling the articulators. It supports control of both the source characteristics (e.g., the vocal pitch) and the vocal tract transfer function (e.g., the formant frequencies) and does so sometimes in rapid response to production changes (e.g., Burnett et al., 1998; Purcell and Munhall, 2006a) as well as in a more predictive fashion (Jones and Munhall, 2005; Houde and Jordan, 1998). In this paper, we focus on the role of auditory feedback in the control of vowel quality and thus on how the sound of the voice is used for the predictive control of the vocal tract transfer function. In this role, sensory feedback is involved in planning the configuration of the oral articulators as well as the scale of their movements.

To use sensory feedback for these purposes, the speech planning system must have a mapping between the movements of the speech articulators and the acoustic spectral consequences of their actions. Thus, the motor planner must “know” that movements of a given type will produce acoustic patterns of a certain kind. This input-output relationship must be a significant component of the speech-motor control system, just as a mapping between different spatial coordinate systems is important for visual-motor and vestibular-motor coordination (Beurze et al., 2006). Many control schemes using such a mapping are possible (e.g., Tin and Poon, 2005), and there is need for systematic data on the input-output relationship for auditory feedback to begin to specify the class of controllers that best represents speech-motor control.

In this paper, we examine vowel formant feedback and the relationship between the magnitude of perturbation and the compensatory response. In general, when talkers hear real-time perturbations of their first or second formant, they compensate by altering the formant frequencies of their utterances in a direction opposite in frequency to the perturbation (Houde and Jordan, 1998; Purcell and Munhall, 2006b; Villacorta et al., 2007; Munhall et al., 2009). These compensations exhibit three consistent characteristics. First, compensation is only observed when perturbations have a magnitude greater than some threshold (Purcell and Munhall, 2006b). Second, compensation behavior exhibits a learning curve. Talkers require multiple trials to reach an asymptotic steady state both when the perturbation is initially applied and when it is removed (e.g., Munhall et al., 2009). Third, average compensation is incomplete (Houde and Jordan, 1998; Purcell and Munhall, 2006b; Villacorta et al., 2007; Munhall et al., 2009). The average change in production is smaller in magnitude than the magnitude of the perturbation applied to the acoustic feedback.

The sensitivity to the scale of the perturbation and thus the gain parameter that governs compensatory behavior has been studied with vocal pitch (Burnett et al., 1998; Liu and Larson, 2007) but has not been examined directly for formant frequency perturbations. Burnett et al. (1998) examined talkers’ responses to pitch shifts ranging from 25 to 300 cents. Over this range, the magnitude of compensation did not vary with the magnitude of the pitch shift. However, the proportion of talkers found to compensate decreased (i.e., more talkers “followed” the perturbation) as the pitch shift was increased in magnitude. Liu and Larson (2007) examined talkers’ responses over a smaller range of pitch shift magnitudes ranging from 10 to 50 cents. Over this range, the magnitude of compensation increased with the magnitude of the pitch shift. While complete compensation (i.e., the magnitude of compensation is equal to that of the pitch shift) was observed for the smallest pitch shift, 10 cents, partial compensation was observed for larger shifts. When measured as a proportion of the pitch shift, the compensation decreased as the perturbation was increased. For the largest pitch shift tested, 50 cents, compensation was approximately 30% that of the perturbation.

The gain in response to sensorimotor perturbations has been studied in eye movements as well as limb movements. Saccadic perturbation experiments also reveal an incomplete response to the perturbation of the perceived target location (Hopp and Fuchs, 2004). In smooth pursuit eye movements, the gain appears to be dynamically controlled (Churchland and Lisberger, 2009). Responses to brief perturbations are significantly enhanced during pursuit movements compared to fixations. Limb movements show complex gain modulation at different levels of the system. At the muscle level, the gain of the short-latency stretch response scales proportionally to the muscle activity prior to the perturbation (Pruszynski et al., 2009). The response of hand movements to visual perturbations is largely proportional to the perturbation but is differentially influenced by motion and position information as well as the timing of the perturbation (Saunders and Knill, 2004). However, learning in such contexts has been shown to generalize to new gains between vision and movement (Krakauer et al., 2000), indicating that gain may be an independent parameter even in complex sensorimotor contexts.

In order to begin to parametrize the formant feedback system, perturbations of different magnitudes must be introduced. Here we use two methods of formant perturbation described in the literature: the large abrupt step change in formant frequency (Munhall et al., 2009) and the ramp of small formant frequency changes (e.g., Purcell and Munhall, 2006b). In Experiment 1, compensation was measured for formant-shifts of three different magnitudes using a within-subjects design. These step-changes in formant frequency involve feedback changes that are static for a number of trials to give subjects time to reach a maximum compensation for the given perturbation. In Experiment 2, the frequency shifts were increased in magnitude in small steps with each utterance. Thus, Experiment 2 provides a much broader range of perturbation magnitudes but involves a dynamic feedback environment that is continually changing away from the normal state. Together, these studies reveal the limits of short-term learning within this feedback system and specify the boundaries of the use of auditory feedback in the control of formant production.

GENERAL METHODS

Equipment

The equipment used was similar to that reported in Munhall et al., 2009. Testing was conducted in an Industrial Acoustics Co. (IAC) sound booth. Talkers were instructed to say words that appeared on a computer monitor at a natural rate and speaking level. Each word prompt lasted 2.5 s and the inter-trial interval was approximately 1.5 s. Talkers spoke into a headset microphone (Shure WH20). This signal was amplified (Tucker-Davis Technologies MA3 microphone amplifier), low-pass filtered with a cut-off frequency of 4500 Hz (Frequency Devices 901 filter for Experiment 1 and Krohn-Hite 3384 filter for Experiment 2), digitized with a sampling rate of 10 kHz and filtered in real-time to produce formant-shifts (National Instruments PXI-8106 controller). The output was amplified and mixed with noise (Madsen Midimate 622 audiometer) and presented over headphones (Sennheiser HD 265) such that the speech and noise were presented at approximately 80 and 50 dBA, respectively.

Online formant-shifting and detection of voicing

Detection of voicing and formant-shifting was performed as previously described in Munhall et al., 2009. Voicing was detected using a statistical amplitude-threshold technique. The formant-shifting was achieved in real-time using an infinite impulse response filter. Formants were estimated every 900 μs using an iterative Burg algorithm (Orfandidis, 1988). Filter coefficients were computed based on these estimates such that a pair of spectral zeroes was placed at the location of the existing formant frequency and a pair of spectral poles was placed at the desired frequency of the new formant.

Estimating model order

The iterative Burg algorithm used to estimate formant frequencies requires a parameter, the model order, to determine the number of coefficients used in the auto-regressive (AR) analysis. Prior to data collection, talkers produced six utterances of seven English vowels in an ∕hVd∕ context (“heed,” “hid,” “hayed,” “head,” “had,” “hawed,” and “who’d”). These utterances were analyzed with model orders ranging from 8 to 12. The best model order for each individual was selected using a heuristic based on minimum variance in formant frequency over a 25 ms segment midway through the vowel.

Offline formant analysis

The procedure used for offline formant analysis was the same as that used by Munhall et al. (2009). The boundaries of the vowel segment in each utterance were estimated using an automated process based on the harmonicity of the power spectrum. These boundaries were then inspected by hand and corrected if required.

The first three formant frequencies were estimated offline from the first 25 ms of a vowel segment using a similar algorithm to that used in online shifting. The formants were estimated again after shifting the window 1 ms and repeated until the end of the vowel segment was reached. For each vowel segment, a single “steady-state” value for each formant was calculated by averaging the estimates for that formant from 40% to 80% of the way through the vowel. While using the best model order reduced gross errors in tracking, occasionally one of the formants was incorrectly categorized as another (e.g., F2 being misinterpreted as F1, etc.). These incorrectly categorized estimates were found and corrected by examining a plot with all the “steady-state” F1, F2, and F3 estimates for each individual.

EXPERIMENT 1

In this experiment, talkers’ compensation was measured for three different formant-shifts using a within-subjects design. Each of the three formant-shifts altered both F1 and F2 such that the vowel ∕ε∕ was shifted toward ∕æ∕. Both formants were shifted to follow the trajectory between ∕ε∕ and ∕æ∕ in the vowel space. The magnitudes of the three shifts were chosen so that the perturbations were small, medium, and large relative to the average difference in production between ∕ε∕ and ∕æ∕. The experiment tested two aspects of the input-output function: (a) whether the compensation magnitude varied linearly with perturbation magnitude across a range of formant values in the vowel space and 9b) whether the tendency toward partial compensation occurred for larger perturbations but not smaller variations in feedback (e.g., Liu and Larson, 2007).

Participants

The participants were 20 male undergraduate students from Queen’s University ranging in age from 18 to 22 years old (M=20.5, SD=1.24). All spoke English as a first language and reported no history of hearing or language disorders. Hearing thresholds between 500 and 4000 Hz were assessed. One additional participant was excluded based on a hearing threshold greater than or equal to 25 dB hearing loss (HL) for at least one of the frequencies tested. All other participants had thresholds less than 25 dB HL.

Procedure

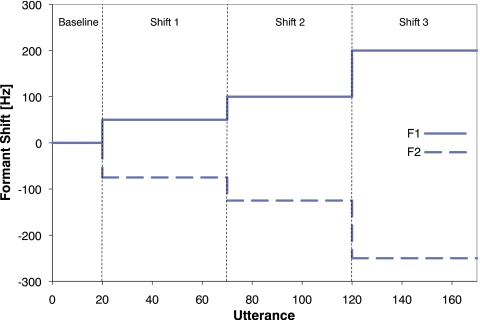
Over the course of Experiment 1, each talker was prompted to say the word “head” a total of 170 times. The experiment consisted of four phases (see Fig. 1). In the first phase, Baseline, 20 utterances were spoken with normal feedback (i.e., amplified and with noise added but no shift in formant frequency) to estimate Baseline F1 and Baseline F2 values. In each of the subsequent three phases, Shifts 1, 2, and 3, talkers produced 50 utterances with altered feedback with F1 increased and F2 decreased in frequency. F1 was increased in frequency by 50, 100, and 200 Hz for Shifts 1, 2, and 3, respectively. F2 was decreased in frequency by 75, 125, and 250 Hz for Shifts 1, 2, and 3, respectively.

Figure 1.

Feedback shift applied to the first formant (solid line) and second formant (dashed line) over for the course of Experiment 1. The vertical dashed lines denote the boundaries of the four phases: Baseline, Shift 1, Shift 2, and Shift 3.

Results

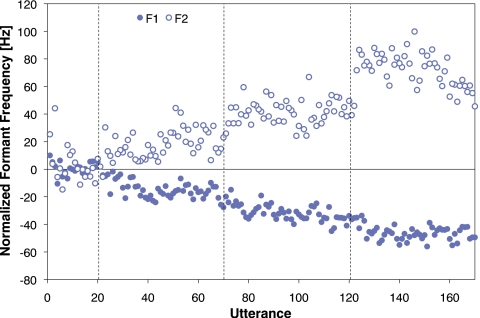
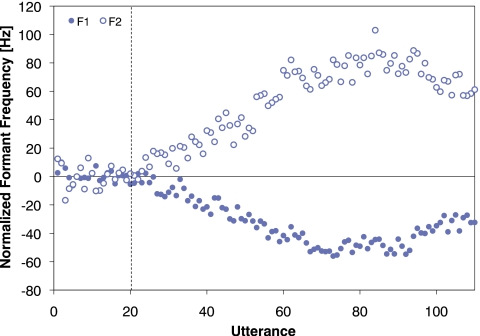
For each individual, the baseline average productions of F1 and F2 were calculated from the last 15 utterances of the Baseline phase (i.e., utterances 6–20) and the F1 and F2 results were then normalized by subtracting the subject’s baseline average. The normalized results for each utterance, averaged across talkers, can be seen in Fig. 2. In all three phases with altered feedback, talkers, on average, compensated for the altered feedback by changing production of both F1 and F2 in a direction opposite that of the perturbation. Further, the magnitudes of the compensation increased over the three phases.

Figure 2.

Average normalized F1 (solid circles) and F2 (open circles) frequencies for each utterance. The vertical dashed lines denote the boundaries between the four phases of the experiment: Baseline, Shift 1, Shift 2, and Shift 3.

To quantify the change in production, four intervals were defined based on the last 15 utterances in each of the four phases (utterances 6–20 for baseline, 56–70 for Shift 1, 106–120 for Shift 2, and 156–170 for Shift 3). In each interval, it is assumed that formant production has reached a steady state. The F1 and F2 estimates can be seen in Table 1. Repeated measures analyses of variance (ANOVAs) with interval as a within-subjects factor (and using Greenhouse–Geisser correction) confirmed a significant effect for both F1 [F(2.62,57)=30.52, p<0.001] and F2 [F(1.74,57)=13.51, p<0.001]. Multiple pairwise comparisons using Bonferroni correction confirmed that the formant values in all four phases were significantly different from each other for both F1 and F2, (p<0.05), except for the comparison between Shifts 2 and 3.

Table 1.

Mean formant frequency in Hz for the last 15 utterances of each of the four phases in Experiment 1. One standard deviation is given in parentheses.

	Baseline	Shift 1	Shift 2	Shift 3
F1	582.6 (29.9)	562.4 (32.7)	547.8 (28.9)	536.0 (28.4)
F2	1705.8 (80.4)	1727.1 (80.1)	1749.1 (89.7)	1766.5 (88.8)

To directly compare the change in production for each formant for a given perturbation, a compensation measure was computed. Compensation was defined as the difference in production between the last utterances of each shift phase and those of the Baseline phase (i.e., the normalized formant values described above) with the sign of these measures harmonized for the two formants. The sign of the compensation was defined as positive if the change in production was opposed to that of the formant-shift or negative if the compensation followed the direction of the formant-shift. For the largest shift, most talkers compensated in a direction opposed to the formant-shift. However, two talkers exhibited following behavior for F2.

To examine the relationship of the vowel space to the compensation patterns, estimates for F1 and F2 were calculated for the utterances of ∕ɪ∕, ∕ε∕, and ∕æ∕ (“hid,” “head,” and “had,” respectively) from the vowels collected at the onset of the experiment to determine the model order for formant tracking. For each vowel, the F1 and F2 estimates from each utterance were considered as joint random variables whose means varied across individuals. The data were normalized by subtracting the individual’s average and adding the population average formant frequency. For each vowel, the results were pooled to estimate the distribution of F1 and F2 for an average talker’s utterance of that vowel.

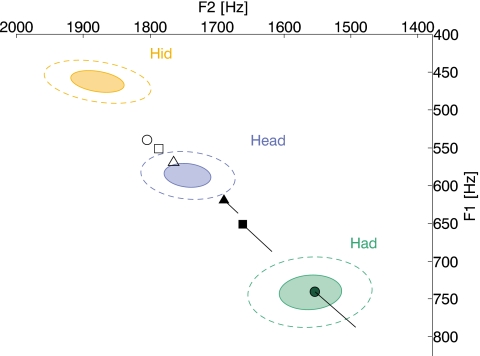
Each concentric ellipse in Fig. 3 indicates the distribution of an average talker’s production of ∕ɪ∕, ∕ε∕, and ∕æ∕ in an ∕hVd∕ context. The center of each pair of ellipses indicates the mean F1 and F2, while the solid and dashed ellipses indicate one and two standard deviations, respectively. The results from Experiment 1 have been superimposed on this portion of an average talker’s vowel space. The open symbols indicate the average-steady-state production for Shifts 1, 2, and 3 (the triangle, square, and circle symbols, respectively). Similarly, the filled symbols indicate the average-steady-state acoustic feedback for Shifts 1, 2, and 3 (the triangle, square, and circle symbols, respectively). The three straight lines indicate the effect of compensation on the acoustic feedback. If talkers did not compensate, then the acoustic feedback that they would have heard is indicated by the ends of the lines opposite the filled symbols.

Figure 3.

Experiment 1 results superimposed on an average talker’s production of ∕ɪ∕, ∕ε∕, and ∕æ∕. Each pair of concentric ellipses indicates the distribution of an average talker’s production of ∕ɪ∕, ∕ε∕, and ∕æ∕ in an ∕hVd∕ context. The center of each pair of ellipses indicates the mean production of an average individual and the solid and dashed ellipses indicate 1 and 2 standard deviations, respectively. The average-steady state results for Shifts 1, 2, and 3 are indicated by the triangle, square, and circle symbols, respectively. Open symbols indicate the average production, while the filled symbols indicate the average acoustic feedback. The three lines indicate the effect of compensation on the acoustic feedback. The ends of the lines opposite the filled symbols indicate the acoustic feedback talkers would have heard if they did not compensate.

To examine the effect of individual vowel space differences on compensation, a correlation analysis was performed. For each individual, the average compensations in F1 and F2 for the largest shift condition were combined as components of a compensation vector in the vowel space. Similarly, vectors were computed based on the difference between average production of ∕ε∕ and ∕æ∕ for each individual. No significant correlation was found between the magnitudes of these two vectors. Further, no significant correlation was found when this analysis was repeated comparing compensation with individual differences between ∕ε∕ and ∕æ∕.

Discussion

In this experiment, the compensations to three pairs of formant perturbations were measured. As in our previous work on large, abrupt formant perturbations (Munhall et al., 2009), the observed compensations exhibited learning curves that are approximately exponential and asymptote at a level of partial compensation. Subjects on average compensated 17.4, 34.9, and 46.6 Hz for perturbations in F1 of 50, 100 and 200 Hz. For F2, the compensations were similarly partial with compensations of 21.2, 43.3, and 60.7 Hz being observed for perturbation magnitudes of 75, 125, and 250 Hz. For both formants, the overall compensation function has significant non-linear components. While larger compensations are observed as shift magnitude is increased, the marginal increase in compensation is proportionally smaller than the marginal increase in shift magnitude. The general compensation patterns were not obviously related to the spacing of adjacent vowels in the vowel space.

For all perturbation magnitudes, the compensation response was partial. However, this is not a consequence of an inherent limitation in compensatory ability. As illustrated in Fig. 3, the average-steady-state compensation observed for Shift 3 is approximately the same magnitude as the perturbation applied in Shift 1. Indeed, the average compensations in Shift 3 are 46.6 and 60.7 Hz for F1 and F2, respectively. Thus, even though talkers were capable of fully compensating for small formant-shifts, only partial compensation was observed. Partial compensation has been consistently reported in previous studies (Houde and Jordan, 1998; Purcell and Munhall, 2006b; Villacorta et al., 2007) in which different perturbation protocols were used (e.g., small perturbations on each trial), and thus partial compensation is not a function of the sudden large feedback changes used here. A number of possible explanations exist for this pattern. The sensory feedback used to control speech production is not limited to audition. Somatosensory feedback, for example, also plays a role in speech production (Tremblay et al., 2003; Nasir and Ostry, 2008). When talkers compensated for the altered auditory feedback in our experiment, their change in production would produce a discrepancy in somatosensory feedback. One possibility is that the observed partial compensation is a result of the control system minimizing error across both sensory systems. Partial compensation has also been observed in saccadic adaptation, and Hopp and Fuchs (2004) suggested that the adaptation process might involve two components. The first is a rapid partial compensation followed by a very slow recalibration that is not completed in the limited time course of laboratory studies. Similar proposals have been made for two components in the adaptation process for arm movements in novel force fields (Smith et al., 2006). This possibility exists for auditory feedback perturbation as well, since the exposure to altered feedback in an experiment is relatively brief.

In summary, the results from Experiment 1 suggest that compensation is partial for all perturbation magnitudes. While the function relating compensation to formant-shift magnitude may be linear for small perturbations, it is non-linear and compressive for large perturbations similar to results for pitch perturbations (Liu and Larson, 2007).

EXPERIMENT 2

In Experiment 1, the formant-shifts were applied as step-changes with each shift condition held constant for many utterances allowing talkers’ compensation to reach steady state. Unfortunately, this methodology is limited as only a few formant-shift conditions can be observed in one session. Another approach is to progressively increase the magnitude of the perturbation of F1 and F2 with each utterance. Using this paradigm, the compensation to a larger number of different formant-shift magnitudes can be observed. Thus, Experiment 2 was conducted both to provide a more detailed estimate of the shape of the compensation function and to explore if the rate at which a perturbation is introduced affects compensation.

Participants

The participants were 21 male undergraduate students from Queen’s University ranging in age from 17 to 24 years old (M=18.5, SD=1.6). All spoke English as a first language and reported no history of hearing or language disorders. All the participants had hearing thresholds less than 25 dB HL for frequencies ranging from 500 to 4000 Hz. None of the talkers participated in Experiment 1.

Procedure

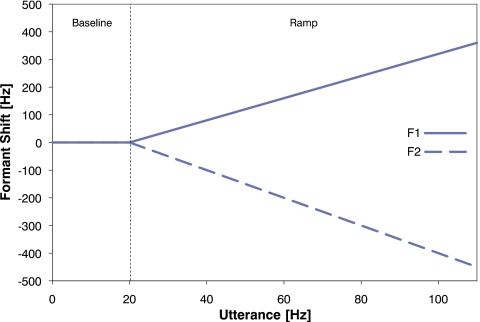
Over the course of Experiment 2, each talker was prompted to say the word “head” a total of 110 times. The experiment consisted of two phases (see Fig. 4). In the first phase, Baseline, 20 utterances were spoken with normal feedback (i.e., amplified and with noise added but no shift in formant frequency) to estimate Baseline F1 and Baseline F2 values. In the second phase, Ramp, the utterances were spoken with altered feedback with F1 increased and F2 decreased in frequency. For each utterance, the magnitudes of the formant-shifts applied to F1 and F2 were increased by 4 and 5 Hz, respectively. Thus, for the 21st utterance, the shifts in frequency of F1 and F2 were +4 and −5 Hz; for the 110th utterance, the shifts in frequency of F1 and F2 were +360 and −450 Hz.

Figure 4.

Feedback shift applied to the first formant (solid line) and second formant (dashed line) over the course of Experiment 2. The vertical dashed line denotes the boundary between the Baseline and Ramp phases.

Results

The normalized formant frequencies for each talker’s utterances were calculated in the same way as in Experiment 1 and the results averaged across talkers can be seen in Fig. 5. In the Ramp phase, talkers altered production of both F1 and F2 in a direction opposite to that of the perturbation. For the first 50 utterances of the Ramp phase (i.e., utterances 21–70), the normalized frequency for both F1 and F2 increased in magnitude approximately linearly. However, on subsequent utterances the magnitude reached a plateau and then began to decrease. To test if this decrease was statistically reliable, the average normalized formant frequency for utterances 66–70 was compared with that of utterances 101–110. For F1, the difference between the two intervals was significant (p=0.01) but for F2 the difference was not significant (p>0.05).

Figure 5.

Average normalized F1 (solid circles) and F2 (open circles) frequencies for each utterance in Experiment 2. The vertical dashed line denotes the boundary between the Baseline and Ramp phases.

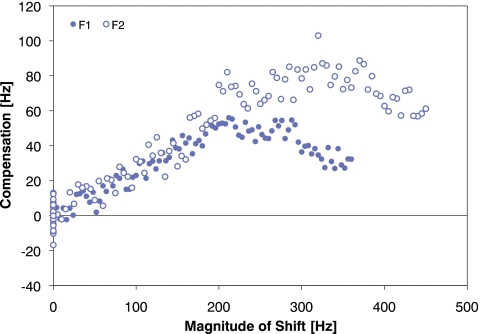
As in Experiment 1, we define compensation as the magnitude of the change in formant frequency from the baseline average with sign based on whether the change opposes (positive) or follows (negative) that of the perturbation. With the exception of one talker, all talkers exhibited positive compensation on average over the interval of utterances 61–70. The compensation, average across all talkers, as a function of frequency-shift magnitude is plotted in Fig. 6. From the figure, it can be seen that the functions for both F1 and F2 are similar in shape. Further, they are similar in magnitude for formant-shifts that are less than 200 Hz in magnitude. The compensations for the two formants, however, do not asymptote at the same level, nor do the compensations begin to decrease at the same point in frequency.

Figure 6.

Compensation, averaged across all talkers, in F1 (solid circles) and F2 (open circles) as a function of the magnitude of formant-shift applied to acoustic feedback. Here, the magnitude of compensation is defined as the magnitude of the average normalized formant frequency. The sign of the compensation is defined as positive when the change in production is opposed to that of the formant-shift and negative when it follows that of the formant-shift.

As can be seen in Figs. 56, production of both F1 and F2 changed approximately linearly over the first 50 utterances of the Ramp phase (utterances 21–70). The magnitudes of the frequency shifts applied during this interval ranged from 4–200 and 5–250 Hz for F1 and F2, respectively. For both F1 and F2, a linear regression was performed on the data from this interval and approximately 90% of the variance was accounted by this linear trend. The compensations for F1 and F2 were found to be approximately 25%–30% of the formant-shift magnitude (see regression values in Table 2).

Table 2.

Linear regression of compensation as a function of frequency shift. The coefficients are based on the data from utterances 21–70 of Experiment 2. The 95% confidence intervals are given in parentheses.

	Slope	Intercept	R2
F1 Compensation	0.260 (±0.021)	−1.04 (±2.47)	0.927
F2 Compensation	0.304 (±0.032)	1.30 (±4.67)	0.882

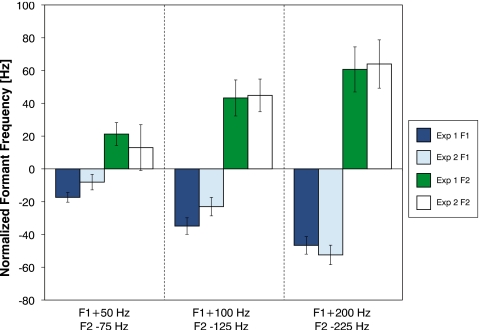
To test whether the small ramp perturbations used in Experiment 2 produce similar changes to those caused by the larger step perturbations used in Experiment 1, we compared the results from utterances in Experiment 2 with the matched utterances from Experiment 1. The compensations for perturbations of equivalent magnitude (100 and 200 Hz for F1 and 75, 125 and 250 for F2) were compared directly. However, in Experiment 2, the F1 perturbation was incremented by 4 Hz per utterance. Thus, there was no utterance for which the perturbation of F1 was 50 Hz (as used in Shift 1 of Experiment 1). A compensation response to a 50 Hz perturbation for F1 was approximated by averaging the compensations for perturbations of 48 and 52 Hz from the Experiment 2 data set and then compared to the result from Experiment 1. In Fig. 7, the average change in normalized formant frequency for these utterances is plotted along with the results from Experiment 1. An examination of Fig. 7 suggests the results of both experiments are quite similar.

Figure 7.

Comparison of compensation between Experiments 1 and 2. The compensations for perturbations of equivalent magnitude were compared directly. However, in Experiment 2, the F1 perturbation was incremented by 4 Hz per utterance. Thus, there was no utterance for which the perturbation of F1 was 50 Hz (as used in Experiment 1). A compensation response to a 50 Hz perturbation for F1 was approximated by averaging the compensations for perturbations of 48 and 52 Hz from the Experiment 2.

This similarity was confirmed with repeated measures ANOVAs, with magnitude of shift as a within-subjects factor and experiment as a between-subjects factor for both F1 and F2. For Experiment 2, four individuals had a tracking error in F2 for one of utterances 35, 34, and 70. Thus, their data have been omitted from the F2 ANOVA. No significant main effect of experiment was found for either F1 [F(1,39)=797.8, p=0.35) or F2 (F(1,35)=1385.0, p=0.59]. As well, no significant interaction of magnitude of shift × experiment was found for F1 [F(2,78)=535.8, p=0.07] or F2 [F(2,70)=535.8, p=0.73].

As in Experiment 1, utterances of seven different vowels were collected prior to conducting formant-shifting to determine the best AR model. Estimates for F1 and F2 were calculated for the utterances with vowels ∕ɪ∕, ∕ε∕, and ∕æ∕ (utterances of “hid,” “head,” and “had,” respectively). The mean and standard deviation of both F1 and F2 from talkers in Experiment 1 and 2 can be seen in Table 3. The approximate end of the linear compensation occurs when perturbations lead to compensating productions of ∕ε∕ that are 1.7 and 1.9 standard deviations away from normal production of F1 and F2, respectively.

Table 3.

Average formant frequencies of three vowels for talkers in Experiments 1 and 2. One standard deviation is given in parentheses.

	∕ɪ∕		∕ε∕		∕æ∕
	F1	F2	F1	F2	F1	F2
Exp. 1	463.0 (15.4)	1878.8 (43.2)	586.5 (17.1)	1744.1 (38.7)	741.0 (24.9)	1560.9 (50.9)
Exp. 2	454.1 (16.4)	1865.6 (44.3)	584.8 (29.4)	1718.8 (41.3)	728.7 (20.2)	1556.4 (44.7)
All	458.5 (16.0)	1872.0 (43.8)	585.7 (24.2)	1731.1 (40.1)	734.7 (22.6)	1558.6 (47.8)

Discussion

The purpose of Experiment 2 was to measure compensation to a large number of formant-shift magnitudes to provide a test of the sensorimotor system’s maximum ability to compensate. For auditory feedback perturbations less than 200 Hz for F1 and 250 Hz for F2, subjects showed linear compensatory changes in response to the incremental changes in feedback, though with slopes less than 1. For larger feedback perturbations, subjects produced formant compensations that were increasingly less effective. The compensatory behavior in both formants approached an asymptote and then started to decrease with increasing perturbation magnitude. The maximum compensation observed in Experiment 2 was comparable to that observed in Experiment 1. These results suggest that the relationship plotted in Fig. 6 is a good estimate of the function relating compensation to the magnitude of formant-shift. Further, this response is independent of how the perturbation is introduced.

The compensation maxima observed for the male participants in this study suggest a fundamental constraint on the range of adaptive behavior based on auditory feedback. These maxima have not been apparent in the literature.Purcell and Munhall (2006b) and Munhall et al. (2009) used F1 perturbations of 200 Hz but did not go beyond this.Villacorta et al. (2007) used slightly smaller maximum perturbations. The present study also used a male population and previous studies tested females or mixed samples. Additional studies of the vowel space and compensation may help clarify the reasons for this ceiling in compensation. In particular, comparisons with data from females who have higher formant values and larger vowel spaces may be informative.

In comparing the maximum compensations of Experiments 1 and 2, it is interesting to note that the adaptation to the first shifts in Experiment 1 did not reduce the overall maximum compensation, indicating that the maximum is not easily modified. This suggests that the long term acoustic targets used by the control system were not altered during the brief time courses of these experiments.

The decrease in compensation for formant-shifts of large magnitude could be due to one or more factors. For some vowels and perturbations, there are physical constraints on the vocal tract that will limit maximum compensation. For example, decreasing F1 for the vowel ∕i∕ would necessitate compensatory tongue movements higher than the position of the palate. However, for the vowel and perturbations tested here, physical constraints on the vowel space do not explain the observed limit on maximum compensation. As discussed previously in Experiment 1, the speech-motor control system also employs proprioceptive feedback. Under perturbed auditory feedback, as vowel production deviates from normal, the difference between proprioceptive and auditory feedback will also increase. Thus, the control system must manage a trade-off between the information provided by these two sensory feedback systems. When the difference between the expected and received acoustic feedback is very large, the control system may ignore or place little weighting on that feedback.

Another possibility is that the response to these large-magnitude formant-shifts is influenced by location of other vowels in the vowel space. From Table 3 we see that for the talkers in Experiment 2, the difference in frequency between an average production of ∕ε∕ and ∕æ∕ is approximately 144 and 162 Hz for F1 and F2, respectively. These values are less than the magnitude of the perturbation that results in maximum compensation. In Experiment 2, compensation does not begin to decrease until the acoustic feedback is shifted approximately 1 standard deviation beyond the average production of ∕æ∕. Once again, comparison with data from female subjects would be informative.

One of the intriguing aspects of the present data is the degree to which F1 and F2 show the same feedback-scaling function. Even though the magnitude of the perturbations on any given trial differed between the formants, the compensatory behavior followed the same linear function (see Fig. 6). This is consistent with the idea that the auditory-motor error signal is processed in linear frequency for both formants. Since F1 and F2 frequencies and their perturbations span a broad region of frequency space, the similar behavior suggests that a unit change in frequency anywhere in that space is treated equally by the motor system. In contrast, vowel data from listening experiments are well accounted for by perceptual spaces that reflect the nonlinearities of pitch perception and the increasing bandwidth of peripheral auditory filters with increasing filter center frequency (see Rosner and Pickering, 1994). The linearity across the F1∕F2 response corresponds with the findings of Purcell and Munhall (2006b) that raising and lowering F1 by 200 Hz produced compensations of the same size. One implication of these findings is that feedback perception may involve processes unique from standard speech perception. Zheng et al. (2009) showed that the neural correlates of feedback processing are distinct from listening to recordings of the same speech.

GENERAL DISCUSSION

Over the course of Experiments 1 and 2, talkers were exposed to altered auditory feedback in which the first and second formants were shifted in frequency. The frequency shifts increased over the course of each experiment: three step-changes in Experiment 1 and a continuously increasing ramp in Experiment 2. In both experiments, talkers compensated by changing the production of F1 and F2 in a manner opposite to that of the formant-shift perturbation. The compensation was incomplete in magnitude, approximately 25%–30% of that of the perturbation for shifts in F1 and F2 up to 200 and 250 Hz, respectively. As larger shifts were applied, compensation reached a plateau and then decreased.

The partial compensation shown in these studies has two aspects that may have different origins. First, the slope of the compensation∕perturbation function is considerably less than 1, indicating that even for smaller feedback discrepancies that could be overcome, the speech-motor system tends to only make fractional adjustments in production. This was seen clearly in Experiment 1 where the compensation that was produced for the largest perturbation would have completely adjusted for the small initial perturbation in the experiment. The second aspect of the partial compensation phenomenon is that there is limit or maximum compensation that is observed. Both of these data patterns are observed for both F1 and for F2.

As indicated above, one possible account for the slope of the compensation function is that somatosensory feedback and auditory feedback jointly govern the speech-motor control system. Thus, sensorimotor control involves multisensory processing and some form of cue integration must take place. The degree to which the speech-motor control system weighs the errors from each modality is not known but evidence from audiovisual perception supports the idea that information from different sensory modalities can be flexibly combined to optimize perception (Burr and Alais, 2006;Larson et al., 2008). In vowel production, the auditory and somatosensory contributions may vary for different vowels and speech contexts. For example, high vowels such as ∕i∕ may have stronger somatosensory information and thus be less reliant on auditory feedback. Individual differences in sensory weightings might also explain the large variance in acoustic compensation observed across individuals (seeMunhall et al., 2009).

Previous studies on pitch compensation have demonstrated complete compensation for small perturbation magnitudes (Liu and Larson, 2007). In contrast, the function relating compensation magnitude to formant perturbation magnitude remains linear with a slope much less than 1 as perturbation magnitude is decreased. The laryngeal and oral systems differ greatly on many neural and biomechanical factors (innervation, somatosensory representation, movement range, mass of the articulators, etc.) as well as the difference in acoustic information being processed. The differences in the completeness of compensation between the two systems may have their origins in many of these factors.

While somatosensory information processing might explain the plateau and decrease in compensation observed for large perturbations, this behavior may also be due to the speech-motor control system rejecting the auditory feedback error as being spurious. For large perturbations, the auditory feedback may deviate far enough from the expected production that the feedback is attributed to some other environmental source or noise and not to the talker’s own voice. Breakdowns in illusions such as the “rubber hand” illusion occur when the spatial orientation or position (Costantini and Haggard, 2007) or size of the visual stimulus (Pavani and Zampini, 2007) deviate beyond an acceptable range. For the creation of a perceived body image representation, there are limits for acceptable sensory information. The results of both experiments suggest that if a rejection of unacceptable sensory information occurs for auditory feedback, it requires very large perturbations with magnitudes greater than the difference between adjacent vowels (Table 3).

In both experiments, F1 and F2 were perturbed simultaneously. So far, our analysis has examined the compensation in both formants independently. However, the motor control system may or may not be able to compensate for perturbations in both formants independently. The system may preferentially compensate for perturbations of one formant over another. Alternatively, the system may attempt to compensate in a manner that requires coordinated changes in the two formants. For example, if the direction of compensation is opposite that of the perturbation in an F2-F1 vowel space plane, this will yield a specific relationship between F1 and F2.

This relationship between F1 and F2 can be shown more formally. Let ΔF1 and ΔF2 represent the magnitudes of formant-shifts applied to F1 and F2, respectively, and let C_F1(ΔF1) and C_F2(ΔF2) represent the compensations in F1 and F2 in response to the perturbation. If we assume that the motor control system produces compensation in a direction opposite that of the perturbation, then the following relationship holds:

$$\frac{C_{\text{F}1}\left(\Delta \text{F}1\right)}{C_{\text{F}2}\left(\Delta \text{F}2\right)}=\frac{\Delta \text{F}1}{\Delta \text{F}2}.$$ (1)

In Experiment 2, the ratio of ΔF1 to ΔF2 was held constant. Thus,

$$\Delta \text{F}2=k\Delta \text{F}1.$$ (2)

Substituting Eq. 2 into Eq. 1 and rearranging yield the following relationship between C_F1 and C_F2:

$$k{C}_{\text{F}1}\left(\Delta \text{F}1\right)=C_{\text{F}2}\left(k\Delta \text{F}1\right).$$ (3)

Thus, the assumption that the motor control system produces compensation in a direction opposite that of the perturbation implies a relationship between the compensation and perturbation components. As a result of Eq. 3, if C_F1 is linear then C_F2 is constrained to be linear with identical slope and with an intercept that is a factor of k larger than that of C_F1.

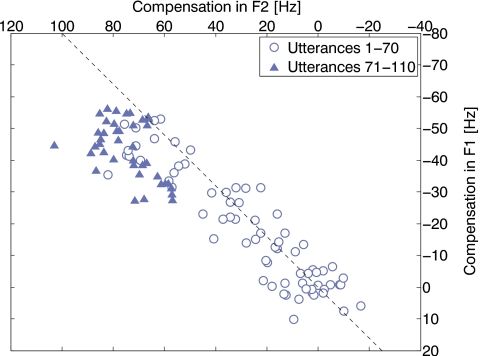
In both experiments, the function relating compensation to formant-shift magnitude is similar for F1 and F2; for the linear portion of the compensatory behavior (Fig. 6), the response slope is the same for both formants. In Fig. 8, the F1 and F2 compensation results from Experiment 2 are plotted in an F1-F2 vowel space context. The dashed line indicates the direction exactly opposite that of the perturbation in the F1-F2 space. The results from the first 70 utterances (circles) lie along the dashed line indicating that compensation was indeed opposite that of the perturbation. The results from the last 40 utterances (triangles) deviate from the dashed line and indicate that compensation is no longer in a direction opposite that of the perturbation. Thus, for the linear portion of the compensatory response (circles), the motor control system is able to compensate in a manner such that the compensations in F1 and F2 are linked. For large perturbations, the compensatory responses are both non-linear and no longer show the proportional linkages between formants. Thus, the proportional linkage between F1 and F2 observed for the first 70 utterances is a controlled response and not a physical necessity imposed by vocal tract geometry.

Figure 8.

Scatter plot of F1 and F2 compensation results from Experiment 2 plotted in an F1-F2 vowel space context. The dashed line indicates the direction geometrically opposite that of the perturbation in the F1-F2 space. The results from the first 70 utterances (circles) lie along the dashed line indicating that compensation was directly opposite that of the perturbation. The results from the last 40 utterances (triangles) deviate from the dashed line and indicate that compensation is no longer in a direction opposite that of the perturbation.

Vowels in the English front vowel space vary along both F1 and F2 and as the vowels move from high to low vowel positions, they move progressively from front to back. Thus, front vowel differences on average form an angular trajectory in linear formant space. Our perturbations in this study are along this formant path as were the perturbations used by Houde and Jordan (2002). The degree to which the structure of the front vowel space constrains the direction and magnitude of compensatory behavior cannot be determined by the present data. However, the results of both experiments suggest that the error in auditory feedback used by the motor control system is not dependent on the spacing of vowels nor presumably by their category boundaries.

If the feedback error was processed post-categorically, then one would expect very little compensation for small formant-shift magnitudes and a sudden large increase in compensation once the formant-shift magnitudes crossed a categorical threshold. This behavior was not observed in Experiment 2. The results suggest that the function relating compensation to formant-shift magnitude is approximately linear for perturbations spanning the interval between two adjacent vowels. Thus, the control system is responding to a difference between the intended and received formant frequencies and not a difference between the intended and received vowel categories. This allows auditory feedback to be used for tighter control of formant frequency than would be possible with a system that only acted to maintain vowel category identity.

The emerging view is a system that maps linear formant frequency to movements over a restricted range surrounding a vowel. This mapping is involved in partially compensating for mismatches in auditory feedback within a few utterances and thus acts as a rapid stabilizing system for speech motor control. The relative independence of the spatial movement dimensions in the vocal tract, and thus formant independence, is unknown and requires additional studies.