Determination of Ensemble-Average Pairwise Root Mean-Square Deviation from Experimental B-Factors

Abstract

Root mean-square deviation (RMSD) after roto-translational least-squares fitting is a measure of global structural similarity of macromolecules used commonly. On the other hand, experimental x-ray B-factors are used frequently to study local structural heterogeneity and dynamics in macromolecules by providing direct information about root mean-square fluctuations (RMSF) that can also be calculated from molecular dynamics simulations. We provide a mathematical derivation showing that, given a set of conservative assumptions, a root mean-square ensemble-average of an all-against-all distribution of pairwise RMSD for a single molecular species, <RMSD²>^1/2, is directly related to average B-factors (<B>) and <RMSF²>^1/2. We show this relationship and explore its limits of validity on a heterogeneous ensemble of structures taken from molecular dynamics simulations of villin headpiece generated using distributed-computing techniques and the Folding@Home cluster. Our results provide a basis for quantifying global structural diversity of macromolecules in crystals directly from x-ray experiments, and we show this on a large set of structures taken from the Protein Data Bank. In particular, we show that the ensemble-average pairwise backbone RMSD for a microscopic ensemble underlying a typical protein x-ray structure is ∼1.1 Å, under the assumption that the principal contribution to experimental B-factors is conformational variability.

Introduction

The most frequently used measure for structure comparison in structural biology is, arguably, the atom-positional root mean-square deviation (RMSD) obtained after roto-translational least-squares fitting (1–5). Its applications are diverse and include monitoring structural changes in simulations of protein folding and dynamics (6–12), evaluating the quality of structure prediction schemes (13–16), comparing the diversity of model structures derived from experiments (17,18), assessing the properties of modeling approaches at different levels of resolution (19,20), and defining high-resolution shapes of polymers (21). Furthermore, structural diversity of an ensemble of biomolecular structures obtained through computer simulations is analyzed frequently by calculating an all-against-all distribution of RMSD values (pairwise RMSD) (22,23). Such calculation is also carried out commonly in NMR spectroscopy to assess the mutual similarity of the lowest energy structures in an ensemble produced by the refinement process (24–26). The resulting distribution of pairwise RMSD values captures the degree of structural heterogeneity of a given ensemble that can be due to either the intrinsic flexibility of a given structure or the uncertainties of the refinement procedure. The properties of this distribution, calculated typically for backbone atoms, are often summarized by reporting its arithmetic mean. Even though the calculations of pairwise RMSD values can be computationally demanding for large ensembles, they are also frequently used as an appropriate measure for clustering of structures (7,27–29).

A distribution of pairwise RMSD values provides information on the mutual similarity of members of a given ensemble when it comes to their global structure. However, to obtain information on local structural flexibility, thermal stability, and heterogeneity of macromolecules, root mean-square fluctuations (RMSF) are often studied (30–32). Most importantly, RMSF can be obtained through Debye-Waller or temperature factors (B-factors) in x-ray experiments using Eq. 1, where B-factors are usually defined as a measure of spatial fluctuations of atoms around their average position and where their motion is described as an isotropic Gaussian distribution of displacements about the average position (33). The inverse of this equation has often been used in the literature to calculate B-factors from various models (most often molecular dynamics simulations or Gaussian network models) and to compare them to experimental values (34–42):

$${\mathit{RMSF}}_{\mathrm{i}}^2=\frac{3B_{\mathrm{i}}}{8{\pi }^2}\text{.}$$ (1)

B-factors have also been used in a variety of studies to predict protein flexibility (43,44), assess their thermal stability (45–47), test for errors in protein structures (48), analyze active sites and binding pockets (49–51), correlate side-chain mobility with conformation (52,53), investigate crystal packing contacts (54), analyze and predict protein disordered regions (55–58), and study protein dynamics (37,40,59). However useful B-factors may be, one should always keep in mind that they include not only the positional variance of macromolecules that is due to local thermal motion, but also the effects of noise due to refinement errors, lattice defects, crystal contacts, and rigid-body motions (36,41,60). Furthermore, they also contain components coming from both static and dynamic disorder (61,62) whose separation is nontrivial (36). Finally, RMSF can also be predicted from NMR chemical shifts via a measure called random coil index (63–65).

Because pairwise RMSD, B-factors (or RMSF) are all frequently used to give information on different aspects of biomolecular ensembles, we study their relationship. We present a derivation showing that, given a set of conservative assumptions, <RMSD²>^1/2 is directly proportional to average experimental B-factors (<B>), i.e., <RMSF²>^1/2 for a single molecular species. Our finding is illustrated and its limits of validity probed by calculations made on structures taken from molecular dynamic (MD) simulations of the native and unfolded state of the villin headpiece domain (10,66) generated using worldwide-distributed computing techniques. In particular, we use simulated ensembles to study the effects of the exact method of structure alignment on the derived relationship, and show that the influence is typically only marginal. Finally, the newly derived relation is used to calculate quadratic means of pairwise RMSD distributions for a set of x-ray structures, given the B-factors reported in the Protein Data Bank (PDB), to assess their heterogeneity in the crystal environment.

To foreshadow the derivation presented in this study, we would like to introduce a useful analogy between <RMSD²>^1/2 and <RMSF²>^1/2 on the one hand and the radius of gyration (R_g) on the other. The radius of gyration, a measure often used to describe the dimensions of biopolymers such as proteins (67–69), can be analytically calculated in two ways: one using the pairwise distances between monomers (Eq. 2, Fig. 1 A), and the other using the distances between each monomer and their center of mass, i.e., the average position of all monomers if they have the same mass (Eq. 3, Fig. 1 B).

$$R_{\mathrm{g}}^2=\frac{1}{2N_{\mathrm{m}}^2}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{m}}}\sum _{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{m}}}{\Vert {\overrightarrow{r}}_{\mathrm{i}}-{\overrightarrow{r}}_{\mathrm{j}}\Vert }^2,$$ (2)

$$R_{\mathrm{g}}^2=\frac{1}{N_{\mathrm{m}}}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{m}}}{\Vert {\overrightarrow{r}}_{\mathrm{i}}-\langle \overrightarrow{r}\rangle \Vert }^2\text{.}$$ (3)

Figure 1.

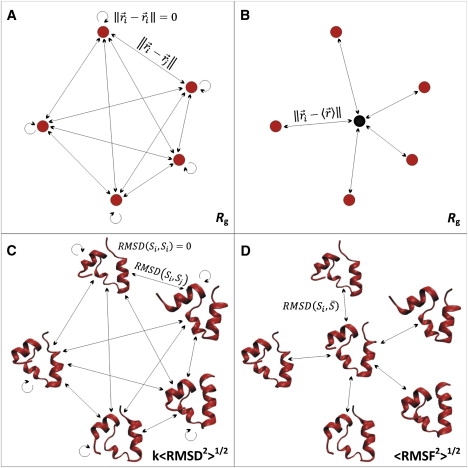
Analogy connecting <RMSD²>^1/2 and <RMSF²>^1/2 with the radius of gyration. (A) For a polymer consisting of N_m monomers, the radius of gyration can be calculated as a root mean-square average over all pairwise distances between monomers as shown in Eq. 2. (B) Another way of calculating the radius of gyration is through distances between monomers and their average position shown in Eq. 3. Analogously to the two ways of calculating R_g, there is equivalence between the root mean-square average of pairwise RMSD for a set of structures (<RMSD²>^1/2) (C) and the root mean-square average deviation from the average structure (<RMSF²>^1/2) (D), as shown in this study. k is a multiplicative factor that is a function of N_s (see Eq. 19). Villin structures in C and D have been prepared by VMD v1.8.6 (85).

Indices i and j refer to different monomers, whereas N_m is a total number of monomers in a chain. Vector $\overrightarrow{r}$ represents spatial coordinates of a monomer, whereas $\langle \overrightarrow{r}\rangle$ is the average position of N_m monomers. Equations 2 and 3 are shown to be identical by modifications of the Lagrange's theorem (70).

Our derivation of the relationship between <B>, <RMSF²>^1/2, and <RMSD²>^1/2, which is the main result of this study, mirrors the relationship between these two definitions of the radius of gyration. Namely, the two definitions given for R_g can be applied easily to ensembles of biomolecular structures where monomers are replaced by structures and RMSD is used as a measure of distance between them (Eq. 2, Fig. 1, C and D). Following this analogy, there is equivalence between root mean-square average pairwise RMSD, <RMSD²>^1/2 (recalling the first definition of R_g, see Eq. 2) and the root mean-square average deviation between each structure and the average structure of the ensemble, <RMSF²>^1/2 (recalling the second definition of R_g, see Eq. 3). The exact relationship between <RMSD²>^1/2, <RMSF²>^1/2, and <B> is explored below, together with an analysis of a novel measure of structural diversity in ensembles, the structural radius (R_struct), which can be thought of as a structural analog of R_g.

Materials and Methods

Molecular dynamics simulations

Thousands of tens of nanoseconds long, independent trajectories for the villin headpiece domain were generated using a heterogeneous computer cluster as a part of the ongoing Folding@Home distributed computing project (10,66). The folding simulations were initiated from fully extended conformations (ϕ = −135°, ψ = 135°) with N-acetyl and C-amino caps. The equilibrium simulations were started from the experimental NMR structure of the molecule (PDB code 1VII, average structure) (66). The simulations, run using Tinker biomolecular simulation package, involved Langevin dynamics in implicit GB/SA solvent (71) (velocity damping parameter of γ = 91 ps⁻¹) with a 2-fs integration step, at 300 K. Bond lengths were constrained using RATTLE (72). No cutoffs were used for electrostatics. The protein was modeled using the OPLSua force field (73). The molecule in the equilibrium simulations was stable with respect to both secondary and tertiary structure (10,74).

The structures were divided into two data sets for calculations: one that included native-like structures (1543 structures taken from the same number of independent equilibrium simulations at t = 20 ns), whereas the other one contained unfolded structures 5213 structures taken from the same number of independent folding trajectories at t = 27 ns).

RMSD calculations—pairwise alignment

To illustrate the relationship between average RMSD and RMSF for ensembles spanning a large range of average RMSD values, we used a clustering procedure on the two villin data sets. The main purpose of this procedure was to derive a set of mutually different distributions of pairwise RMSD to help us illustrate and assess the properties of the derivation provided in this study. Backbone atoms for each pair of structures from both simulated data sets were optimally aligned (pairwise alignment (PA)) before RMSD calculations. Nonweighted pairwise RMSDs were then calculated for the aligned backbone atoms that included C, N, and C_α of every residue (108 atoms in total). A distribution of the calculated pairwise RMSD values was plotted and divided into 20 equal segments between the smallest and the largest RMSD value. The structure that appeared in the highest number of pairs in a given segment was chosen as the center of a cluster, and the structures paired with it were assigned to that particular cluster as well. Twenty clusters were obtained through such a procedure for each data set (number of structures in each cluster is listed in Table S1 in the Supporting Material). Nonweighted pairwise RMSD was calculated for each cluster in the same way as described above using backbone-based PA. Quadratic mean of pairwise RMSD for each cluster was calculated as well.

We have noticed that the choice of the reference structure for the alignment of all the structures before calculating RMSF does affect its quadratic value in the very heterogeneous data set as shown in the Results. Therefore, RMSF for each cluster was calculated by using every single structure from the cluster for the alignment before the calculations and then quadratically averaging the obtained values to get the RMSF value for each cluster. All the alignments and calculations were done by using GROMACS-3.3 and its routines (75).

RMSD calculations—reference structure alignment

Backbones of all the structures were aligned to the backbone of the native structure of the villin headpiece domain taken from the PDB (average NMR structure, PDB code 1VII) (reference structure alignment (RSA)) to rule out the alignment effect from the calculations. Fitted structures were then subjected to the same procedure described in the previous section to obtain clusters (number of structures in each cluster is also listed in Table S1) and quadratic averages of RMSD and RMSF values. Structures were aligned to the reference structure using the McLachlan algorithm (76) as implemented in the program ProFit v3.1 (Martin, A.C.R., http://www.bioinf.org.uk/software/profit/).

Results

Demonstration of a direct proportionality between <RMSD²>^1/2 and <RMSF²>^1/2

RMSD is defined as the root mean-square-average distance between atoms of two optimally superimposed macromolecules (S_i and S_j) and is calculated as a minimum over all rotations and translations of one of the structures being compared (Eq. 4).

$$\mathit{RMSD}\left(S_{\mathrm{i}},S_{\mathrm{j}}\right)=\min {\left(\frac{1}{N_{\mathrm{a}}}\sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{a}}}{\Vert {\overrightarrow{r}}_{\text{ik}}-{\overrightarrow{r}}_{\text{jk}}\Vert }^2\right)}_{\text{rot},\text{trans}}^{\frac{1}{2}},$$ (4)

where N_a is the number of atoms in a structure and should not be confused with the Avogadro constant. Indices i and j refer to different structures, whereas the index k refers to the atom position in a given structure. Vector $\overrightarrow{r}$ represents spatial coordinates of a given atom.

To capture the properties of a distribution of pairwise RMSD, in this study we have used its quadratic mean calculated using Eq. 5 as it lends itself to better analytic manipulation compared to the arithmetic mean that is usually reported in NMR studies.

$${\langle {\mathit{RMSD}}^2\rangle }^{1/2}=\sqrt{\frac{2}{N_{\mathrm{s}}\left(N_{\mathrm{s}}-1\right)}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_s-1}\sum _{\mathrm{j}>\mathrm{i}}^{{\mathrm{N}}_{\mathrm{s}}}{\mathit{RMSD}}^2\left(S_{\mathrm{i}},S_{\mathrm{j}}\right)},$$ (5)

where N_s is the number of structures in an ensemble. Here and in the rest of the derivation we will assume that all the structures are aligned to the same reference structure (therefore, the notation from Eq. 4 was simplified). Note that for the derivation it is not relevant what the exact nature of the reference structure is, as long as the same structure is used for aligning the whole ensemble. This is to be contrasted with typical calculation of pairwise RMSD, where each pair of structures is mutually superimposed.

RMSF for a specific number of structures is defined as a root mean-square-average distance between an atom and its average position in a given set of structures (Eq. 6)

$${\mathit{RMSF}}_{\mathrm{k}}=\sqrt{\frac{1}{N_{\mathrm{s}}}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}{\Vert {\overrightarrow{r}}_{\text{ik}}-{\langle \overrightarrow{r}\rangle }_{\mathrm{k}}\Vert }^2},$$ (6)

where ${\langle \overrightarrow{r}\rangle }_{\mathrm{k}}$ is the average position of the atom k over N_s structures (Eq. 7)

$${\langle \overrightarrow{r}\rangle }_{\mathrm{k}}=\frac{1}{N_{\mathrm{s}}}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}{\overrightarrow{r}}_{\text{ik}}\text{.}$$ (7)

In the following, we have used the quadratic mean of RMSF calculated using Eq. 8

$${\langle {\mathit{RMSF}}^2\rangle }^{1/2}=\sqrt{\frac{1}{N_{\mathrm{a}}}\sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{a}}}{\mathit{RMSF}}_{\mathrm{k}}^2}\text{.}$$ (8)

If Eq. 6 is inserted into Eq. 8,

$${\langle {\mathit{RMSF}}^2\rangle }^{1/2}=\sqrt{\frac{1}{N_{\mathrm{a}}}\sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{a}}}\frac{1}{N_{\mathrm{s}}}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}{\Vert {\overrightarrow{r}}_{\text{ik}}-{\langle \overrightarrow{r}\rangle }_{\mathrm{k}}\Vert }^2}\text{.}$$ (9)

On the other hand, if Eq. 4 is inserted into Eq. 5,

$${\langle {\mathit{RMSD}}^2\rangle }^{1/2}=\sqrt{\frac{2}{N_{\mathrm{s}}\left(N_{\mathrm{s}}-1\right)}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}-1}\sum _{\mathrm{j}>\mathrm{i}}^{{\mathrm{N}}_{\mathrm{s}}}\frac{1}{N_{\mathrm{a}}}\sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{a}}}{\Vert {\overrightarrow{r}}_{\text{ik}}-{\overrightarrow{r}}_{\text{jk}}\Vert }^2}\text{.}$$ (10)

The sums in Eq. 10 can be rearranged

$${\langle {\mathit{RMSD}}^2\rangle }^{1/2}=\sqrt{\frac{1}{N_{\mathrm{a}}}\sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{a}}}\frac{2}{N_{\mathrm{s}}\left(N_{\mathrm{s}}-1\right)}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}-1}\sum _{\mathrm{j}>\mathrm{i}}^{{\mathrm{N}}_{\mathrm{s}}}{\Vert {\overrightarrow{r}}_{\text{ik}}-{\overrightarrow{r}}_{\text{jk}}\Vert }^2}\text{.}$$ (11)

The sums over N_a can now be written

$${\langle {\mathit{RMSD}}^2\rangle }^{1/2}=\sqrt{\frac{1}{N_{\mathrm{a}}}\sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{a}}}\frac{2N_{\mathrm{s}}^2}{N_{\mathrm{s}}\left(N_{\mathrm{s}}-1\right)}\frac{1}{2N_{\mathrm{s}}^2}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}\sum _{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{s}}}{\Vert {\overrightarrow{r}}_{\text{ik}}-{\overrightarrow{r}}_{\text{jk}}\Vert }^2}\text{.}$$ (12)

For simplicity, let us define a new variable

$$R_{\mathrm{k}}^2=\frac{1}{N_{\mathrm{s}}}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}{\Vert {\overrightarrow{r}}_{\text{ik}}-{\langle \overrightarrow{r}\rangle }_{\mathrm{k}}\Vert }^2=\frac{1}{N_{\mathrm{s}}}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}\left({\overrightarrow{r}}_{\text{ik}}^2-2{\overrightarrow{r}}_{\text{ik}}{\langle \overrightarrow{r}\rangle }_{\mathrm{k}}+{\langle \overrightarrow{r}\rangle }_{\mathrm{k}}^2\right)=-{\langle \overrightarrow{r}\rangle }_{\mathrm{k}}^2+\frac{1}{N_{\mathrm{s}}}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}{\overrightarrow{r}}_{\text{ik}}^2\text{.}$$ (13)

The first term on the right-hand side of Eq. 13 can be separated by applying Eq. 7 and the second term can be represented as a double summation over the number of structures

$$R_{\mathrm{k}}^2=-\left(\frac{1}{N_{\mathrm{s}}}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}{\overrightarrow{r}}_{\text{ik}}\right)\left(\frac{1}{N_{\mathrm{s}}}\sum _{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{s}}}{\overrightarrow{r}}_{\text{jk}}\right)+\frac{1}{2N_{\mathrm{s}}^2}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}\sum _{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{s}}}\left({\overrightarrow{r}}_{\text{ik}}^2+{\overrightarrow{r}}_{\text{jk}}^2\right)\text{.}$$ (14)

Terms in Eq. 14 can be added

$$R_{\mathrm{k}}^2=\frac{1}{2N_{\mathrm{s}}^2}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}\sum _{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{s}}}\left(-2{\overrightarrow{r}}_{\text{ik}}{\overrightarrow{r}}_{\text{jk}}+{\overrightarrow{r}}_{\text{ik}}^2+{\overrightarrow{r}}_{\text{jk}}^2\right)=\frac{1}{2N_{\mathrm{s}}^2}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}\sum _{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{s}}}{\Vert {\overrightarrow{r}}_{\text{ik}}-{\overrightarrow{r}}_{\text{jk}}\Vert }^2\text{.}$$ (15)

By combining Eqs. 13 and 15, we now see that

$$R_{\mathrm{k}}^2=\frac{1}{N_{\mathrm{s}}}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}{\Vert {\overrightarrow{r}}_{\text{ik}}-{\langle \overrightarrow{r}\rangle }_{\mathrm{k}}\Vert }^2=\frac{1}{2N_{\mathrm{s}}^2}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}\sum _{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{s}}}{\Vert {\overrightarrow{r}}_{\text{ik}}-{\overrightarrow{r}}_{\text{jk}}\Vert }^2\text{.}$$ (16)

Using the former definition of $R_{\mathrm{k}}^2$ in Eq. 16, we can express <RMSF²>^1/2 (Eq. 9) as

$${\langle {\mathit{RMSF}}^2\rangle }^{1/2}=\sqrt{\frac{1}{N_{\mathrm{a}}}\sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{a}}}{R}_{\mathrm{k}}^2}\text{.}$$ (17)

Furthermore, we can express <RMSD²>^1/2 (Eq. 12) as

$${\langle {\mathit{RMSD}}^2\rangle }^{1/2}=\sqrt{\frac{1}{N_{\mathrm{a}}}\frac{2N_{\mathrm{s}}}{N_{\mathrm{s}}-1}\sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{a}}}{R}_{\mathrm{k}}^2}\text{.}$$ (18)

Finally, combining Eqs. 1, 17, and 18, a formula is derived that proves that <RMSD²>^1/2 is directly proportional to <RMSF²>^1/2 and, subsequently, B-factors.

$${\langle {\mathit{RMSD}}^2\rangle }^{1/2}=\sqrt{\frac{2N_{\mathrm{s}}}{N_{\mathrm{s}}-1}}{\langle {\mathit{RMSF}}^2\rangle }^{1/2}=\sqrt{\frac{2N_{\mathrm{s}}}{N_{\mathrm{s}}-1}\frac{1}{N_{\mathrm{a}}}\sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{a}}}\frac{3B_{\mathrm{k}}}{8{\pi }^2}}\text{.}$$ (19)

Finally, for N_s ≫ 1,

$${\langle {\mathit{RMSD}}^2\rangle }^{1/2}\approx \sqrt{\frac{2}{N_{\mathrm{a}}}\sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{a}}}\frac{3B_{\mathrm{k}}}{8{\pi }^2}}\text{.}$$ (20)

Exclusion of the ensemble size effect and the derivation of identity

Typical calculations of the average pairwise RMSD for a given ensemble exclude the RMSDs between the same structures (equaling zero). One can show (see below) that this causes the relationship between the average RMSD and RMSF (and subsequently B-factors) to depend on the number of structures in an ensemble as in Eq. 19. This effect, as seen in Eq. 20, vanishes only for a large number of structures in the ensemble. One can define a new measure, R_struct (that we term structural radius), using the following equation instead of Eq. 5 to eliminate the aforementioned effect:

$$R_{\text{struct}}=\sqrt{\frac{1}{2N_{\mathrm{s}}^2}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}\sum _{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{s}}}{\mathit{RMSD}}^2\left(S_{\mathrm{i}},S_{\mathrm{j}}\right)}\text{.}$$ (21)

Combining Eqs. 4 and 21, it follows

$$R_{\text{struct}}=\sqrt{\frac{1}{2N_{\mathrm{s}}^2}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}\sum _{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{s}}}\frac{1}{N_{\mathrm{a}}}\sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{a}}}{\Vert {\overrightarrow{r}}_{\text{ik}}-{\overrightarrow{r}}_{\text{jk}}\Vert }^2}\text{.}$$ (22)

The sums in Eq. 22 can be rearranged

$$R_{\text{struct}}=\sqrt{\frac{1}{N_{\mathrm{a}}}\sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{a}}}\frac{1}{2N_{\mathrm{s}}^2}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}\sum _{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{s}}}{\Vert {\overrightarrow{r}}_{\text{ik}}-{\overrightarrow{r}}_{\text{jk}}\Vert }^2}\text{.}$$ (23)

Equation 16 can be inserted into Eq. 23

$$R_{\text{struct}}=\sqrt{\frac{1}{N_{\mathrm{a}}}\sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{a}}}{R}_{\mathrm{k}}^2}\text{.}$$ (24)

The calculation of the average RMSD and RMSF remains the same as in the previous section, so by combining Eqs. 1, 17, 20, and 24, it follows

$$R_{\text{struct}}={\langle {\mathit{RMSF}}^2\rangle }^{1/2}=\sqrt{\frac{1}{N_{\mathrm{a}}}\sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{a}}}\frac{3B_{\mathrm{k}}}{8{\pi }^2}}\approx \frac{1}{\sqrt{2}}{\langle {\mathit{RMSD}}^2\rangle }^{1/2}\text{.}$$ (25)

With Eq. 25 we have shown that R_struct and <RMSF²>^1/2 are identical and can be linked directly with both <RMSD²>^1/2 and experimental B-factors. In this sense, R_struct serves as a measure of structural diversity of an ensemble of structures that is in an intuitively clear fashion directly related to B-factors, RMSF, and RMSD.

Illustrations of the relationship between the average RMSD and RMSF

To demonstrate the derived relationship between the average values of pairwise RMSD and RMSF, structures taken from distributed-computing MD simulations of villin headpiece domain were used to calculate the two measures. Each data set (native and unfolded) was divided into two sets of 20 clusters based on the distributions of pairwise RMSD values for two types of alignment (PA or reference structure alignment (RSA)). For RSA, all structures were first roto-translationally aligned to a common reference structure before their pairwise RMSD values were calculated. For PA, each individual pair of structures was first optimally aligned before calculating their RMSD. Fig. 2 shows these distributions, their arithmetic means and standard deviations. For the native data set, we can see that distributions of pairwise RMSD are very much alike regardless of the type of the alignment. Their arithmetic means and standard deviations are also very similar: 4.02 ± 1.95 Å for the PA curve and 4.07 ± 2.01 Å for the RSA curve. On the other hand, distributions associated with the unfolded data set and generated with different types of alignment are more different that can be seen from their arithmetic means and standard deviations: 7.38 ± 1.23 Å for the PA curve and 7.86 ± 1.39 Å for the RSA curve. From the given values, it can be seen that RMSD values calculated after aligning structures to a reference structure are higher than the ones calculated after the pairwise alignment. This is, of course, expected as for each individual pair of structures, PA gives by definition the lowest values over all possible roto-translational fittings. To further demonstrate this point, in the inset of Fig. 2 we compare RMSD values calculated using both types of alignment for several hundred randomly chosen pairs of structures from both data sets. It is clear from the inset of Fig. 2 that none of the RMSD values calculated after pairwise alignment of structures is higher than the corresponding values calculated after aligning structures to a reference structure.

Figure 2.

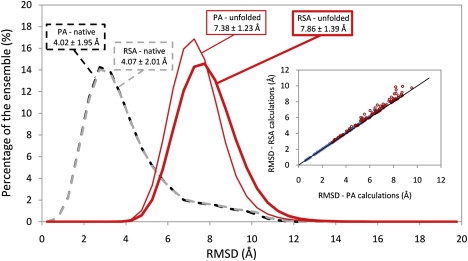
Distributions of backbone pairwise RMSD values of the native and unfolded ensembles of the villin headpiece domain. The dashed black curve represents backbone RMSD values calculated using PA for the native ensemble (<RMSD> = 4.02 ± 1.95 Å). Values for the unfolded ensemble are shown with the thin curve (<RMSD> = 7.38 ± 1.23 Å). Distributions of the corresponding RMSD values calculated using initial alignment to a reference structure (1VII, average structure) (RSA), are shown with the dashed gray curve for the native ensemble (<RMSD> = 4.07 ± 2.01 Å) and with the thick curve for the unfolded ensemble (<RMSD> = 7.86 ± 1.39 Å). The average values and standard deviations for every distribution are also given in the figure. All the values were binned in 0.5 Å bins to generate the distributions. Inset: Relationship between pairwise RMSD values calculated using PA and RSA. For clarity, several hundred randomly chosen points whose values have been taken from the native ensemble are shown as solid circles, whereas several hundred points whose values have been taken from the unfolded ensemble are shown as open circles. The identity line is shown in black.

For every pair of structures belonging to a particular cluster, pairwise RMSD (Eq. 4) was calculated using either PA or RSA, and the quadratic mean of all the RMSD values (Eq. 5) in the given cluster was determined. RSA-calculations were used to study the effect of the optimal alignment on the derived relationship. RMSF for backbone atoms in the cluster was computed as well and its quadratic mean was calculated (Eq. 8). The average values of pairwise RMSD and RMSF for clusters of both data sets and types of alignment are presented in Fig. 3. As can be seen, in the case of RSA, the real data completely agrees with the analytical derivation above (Fig. 3 A). The slope of the trendline shown in Fig. 3 A is in complete agreement with the expected value of 2^1/2 (seen from the derivation) and its squared correlation coefficient (R²) equals 1. However, in the case of PA (Fig. 3 B), the slope of the trendline (1.2968) deviates from the expected value due to the pairwise alignment of structures before calculations, but the R² still has a high value of 0.9956. Deviations caused by the pairwise alignment are smaller for the native data set and the trendline applied to it would have a slope of 1.3862 with an R² of 0.9998 (not shown).

Figure 3.

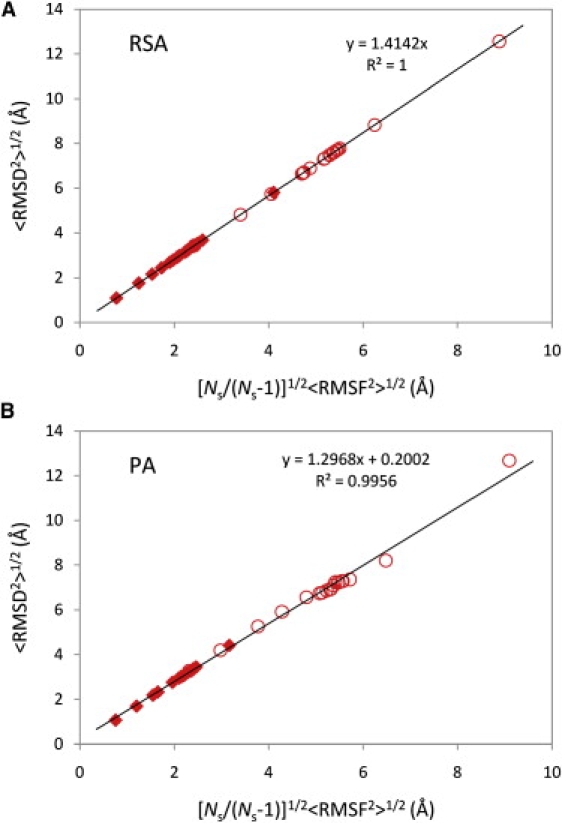
<RMSD²>^1/2 versus [N_s/(N_s-1)]^1/2<RMSF²>^1/2 for native and unfolded state clusters for the villin headpiece domain. <RMSD²>^1/2 values were calculated using Eq. 5, whereas <RMSF²>^1/2 values using Eq. 8. N_s is the number of structures contained in a given cluster. The values for the native ensemble are shown as solid diamonds, and the values for the unfolded ensemble are shown as open circles. In A, all the values have been calculated using RSA, whereas the values in B have been calculated using PA. Trendlines, their analytic expressions, and R² are also shown in the figure.

The relationship shown between RMSD and RMSF explored in Fig. 3 still depends on the number of structures contained in a cluster. That effect can be eliminated by using the structural radius (Eq. 21) as a measure of structural diversity. The calculated values of the structural radius and <RMSF²>^1/2 for clusters of both data sets and types of alignment are presented in Fig. 4. In the case of RSA (Fig. 4 A), both slope of the applied trendline and its squared correlation coefficient equal 1 showing that the two measures are identical and confirming the derivation (Eq. 25). The agreement of the two measures is slightly worse in Fig. 4 Bdue to the pairwise alignment of structures before calculations and the slope of the trendline (0.9099) differs from the expected value of 1, but still has a very high R² of 0.9960. Once more, deviations caused by the pairwise alignment are smaller for the native data set and the trendline applied to it would have a slope of 0.9804 with R² of 0.9999 (not shown). Altogether, one can claim that the effects of the alignment are negligible (<2%) for ensembles with <RMSD²>^1/2 under 4 Å.

Figure 4.

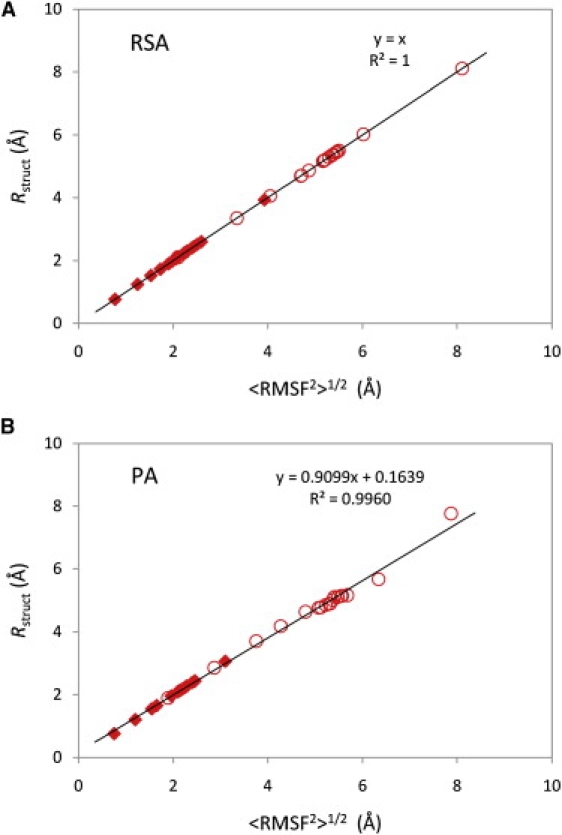
R_struct versus <RMSF²>^1/2 for native and unfolded state clusters for the villin headpiece domain. R_struct values were calculated using Eq. 21, whereas <RMSF²>^1/2 values using Eq. 8. The values for the native ensemble are shown as solid diamonds, and the values for the unfolded ensemble are shown as open circles. In A, all the values have been calculated using RSA. The values in B have been calculated using PA. Trendlines, their analytic expressions, and R² are also shown in the figure.

We also examined how the choice of the reference structure for alignment affects the <RMSF²>^1/2 values, by using every single structure in a given cluster for the alignment before calculations and comparing the obtained distributions of <RMSF²>^1/2 values for every cluster through their arithmetic means and standard deviations. We have also analyzed the maximal and the minimal quadratic means of every cluster to show how extreme the effects of the choice of the reference structure for the alignment can be (Fig. 5). As can be seen from the figure, arithmetic means of both data sets are very close to the minimal values of quadratic means. Their standard deviations are also quite small and they do not exceed the value of 0.26 Å, but they are higher for the unfolded data set. However, for some of the clusters, the difference between the maximal and the minimal value of <RMSF²>^1/2 is more than twofold (e.g., clusters 15 and 18 in the native ensemble) that implies that the choice of the structure for the alignment can make a significant difference for a very diverse data set such as this.

Figure 5.

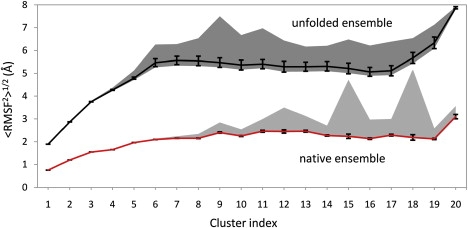
Arithmetic mean, standard deviation and extreme values of quadratic means of RMSF for every cluster. <RMSF²>^1/2 values for every cluster were calculated using Eq. 8, using every structure in the cluster for the alignment before calculation. The lower curve shows arithmetic means of the distributions of quadratic means for native structure clusters. The upper line captures the values for the unfolded structures. Standard deviations of the distributions are shown with black bars. Extreme values and their differences are shown with a light gray area for the native ensemble and with a dark gray area for the unfolded one.

Structural heterogeneity of proteins in crystals

The above relationship between experimental B-factors, <RMSD²>^1/2 and the structural radius provided us with an opportunity to calculate the latter (<RMSD²>^1/2 and R_struct) for an ensemble of structures in a crystal using Eq. 25 and the measured B-factors, thus assessing the heterogeneity of a given crystal. The calculations were made under the assumption that the crystal contains a very large number of structures (N_s ≫ 1) that eliminated cluster size effect. Distributions of <RMSD²>^1/2 and R_struct values for backbone and all atoms for a representative set of x-ray structures from the PDB with ∼4800 structures are presented in Fig. 6 (see the Supporting Material for selection criteria). <RMSD²>^1/2 values for the backbone and all atoms are quite similar: 1.07 ± 0.23 Å for the backbone and 1.13 ± 0.23 Å for all atoms with the maximum values that are <2.5 Å, but still with >6% of structures with <RMSD²>^1/2 >1.5 Å for all atoms. The structural radius values are lower than <RMSD²>^1/2 values, but are still similar: 0.76 ± 0.17 Å for the backbone and 0.80 ± 0.16 Å for all atoms with the maximum values that do not exceed the value of 1.8 Å.

Figure 6.

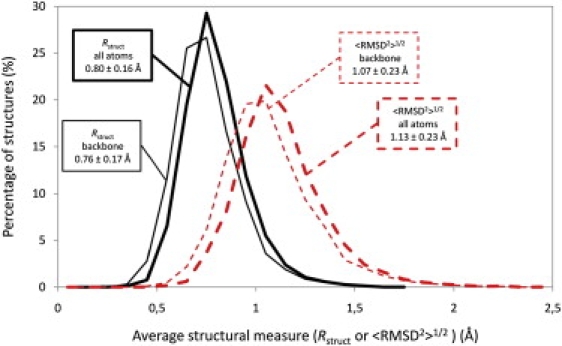
Distributions of root mean-square pairwise RMSD values calculated for x-ray structures. R_struct values calculated using Eq. 25 are represented by the thin solid curve for the backbone atoms with the average of 0.76 ± 0.17 Å and the thick solid curve for all the atoms in the structure (0.80 ± 0.16 Å). <RMSD²>^1/2 values calculated using Eq. 20 are represented by the thin dashed curve for backbone atoms (1.07 ± 0.23 Å) and the thick dashed curve for all the atoms in the structure (1.13 ± 0.23 Å). Average values and standard deviations for every distribution are also shown in the figure. All the values were binned in 0.1 Å bins to generate the distributions.

Discussion

To the best of our knowledge, the heterogeneity of biomolecular ensembles in crystals used in x-ray experiments has never been evaluated previously on the level of pairwise RMSD. Here, we have derived and illustrated a nontrivial relationship between ensemble-average RMSD and RMSF and, subsequently, isotropic B-factors that gave us the opportunity to evaluate the heterogeneity of the microscopic ensembles underlying the typical crystal structures deposited in the PDB. When these values (Fig. 6) are compared to the values for villin headpiece obtained through simulation (Figs. 3 and 4), we can easily see that even the highest values for proteins in a crystal are rather small and coincide with the values for the native data set in the villin graphs, for which the relationship between <RMSD²>^1/2 and <RMSF²>^1/2 is close to exact, regardless of the alignment. The crystal lattice aligns the protein structures to a significant degree such that the RSA would likely be a valid approximation, but it is reassuring to see that the typical values for <RMSD²>^1/2 in crystals occupy the regime in which the choice of alignment makes very little, if any, difference. It is our estimate that if one calculates <RMSD²>^1/2 from B-factors as in Eq. 20, the error committed is <2% on average compared to the ideal-case pairwise alignment. Namely, 2% is the average deviation between the <RMSD²>^1/2 values obtained using RSA and PA for all villin structures below <RMSD²>^1/2 of 4 Å (Fig. 3). It has been proposed recently that a single crystallographic structure deposited in the PDB is not enough to assess the heterogeneity of a crystal and that an ensemble of models would be a more suitable representation (77). Nevertheless, we feel that the identity we have shown in this study is a good starting point for the assessment of crystal heterogeneity that could be generalized to an ensemble of models in a straightforward manner. Finally, the derivation presented here could in future research potentially be generalized to include anisotropic B-factors as well. Due to the additional information present, the associated <RMSD²>^1/2 values would likely be more informative in that case.

Given the analogy between the structural radius and the radius of gyration and our derivation, it becomes obvious that the structural radius can be used for an ensemble of macromolecular structures in the same sense as the radius of gyration is used for a single macromolecular structure. Although the radius of gyration provides information on a macromolecule's size, the structural radius tells how diverse structures in a given ensemble are on a global scale. The structural radius can be calculated either by using pairwise RMSD as a measure of distance between structures (Eq. 21), or by using RMSD values between each structure and the average structure of the ensemble. The latter corresponds to <RMSF²>^1/2 as shown in Eq. 9, but with a difference of first summing over the number of atoms (N_a), and then over the number of structures (N_s), which is actually identical to Eq. 9 because the sums are interchangeable. Note that if the structural radius is calculated in this way, its usage should be restricted to molecular ensembles whose <RMSD²>^1/2 is ≲6 Å (for which the alignment effects are ≲3%). For more heterogeneous ensembles, we would advise to either use the PA approach or simply exercise caution when interpreting results because of the potential deviations at high RMSD values. Here, it should be mentioned that it has been shown previously that the sum of squared distances for all atomic pairs equals the sum of squared distances to the average structure (78). Even though the authors suggested that this connection could be used for speeding up RMSD calculations (as the number of RMSD evaluations is reduced from N_s(N_s − 1)/2 to N_s) and improving algorithms in multiple structure alignment, they made no explicit link between RMSD, RMSF, and B-factors.

An important challenge in quantifying the relationship between RMSF and RMSD is the influence of optimal alignment of two structures on their mutual RMSD value. All the RMSD values calculated after the optimal pairwise alignment of two structures (PA) are lower than the ones calculated after the initial alignment of all the structures to a reference (RSA). Optimal alignment means that roto-translational fitting of the structures is carried out to minimize the RMSD value between them. Now, if one optimally aligns two structures to a reference structure, those two structures will not be optimally aligned with each other and their mutual RMSD will not be minimal, unless all three structures are mutually highly similar. For example, the effect of the optimal alignment is noticeably lesser in the native ensemble of villin than in the unfolded one, because 1), the unfolded ensemble is much more heterogeneous than the native one, and 2), the structure used as a reference is the native form of the villin headpiece domain taken from the PDB. However, as shown here, the effects of the alignment are typically only marginal. Parenthetically, one way of avoiding roto-translational alignment altogether would be to use internal coordinates to represent biomolecules and assess their structural heterogeneity. Nevertheless, as biomolecular structures (including the associated B-factors) are refined in Cartesian coordinates, we believe that the most natural measure for evaluating their global structural diversity directly from experiment should also involve atom-positional Cartesian representation, such as in the case of RMSD. In fact, the mathematical simplicity of the connection between B-factors, RMSF, and RMSD described in this study actually serves as indirect evidence supporting this claim.

In addition, RMSF values are also affected by the choice of the reference structure for the alignment. In Fig. 5, we show the arithmetic mean and standard deviation of distributions of <RMSF²>^1/2 values calculated for every cluster, but differing in the choice of the structure used for the alignment before calculations. Even though the standard deviations throughout the clusters are quite small and they never exceed the value of 0.26 Å, the differences between the maximal and minimal values of quadratic means in some clusters are twofold (Fig. 5), which suggests that the choice of a reference structure in certain rare cases could indeed influence the outcome significantly. Contrary to this finding, Yang et al. (39) found no major effect of the choice of the alignment structure in their studies where they calculated residual RMSD of the ensembles of NMR models. We explain this discrepancy with the greater diversity of structures in our data set compared to most ensembles of NMR models, and we would like to stress the necessity of evaluating the diversity of an ensemble before ruling out the possible effect of the choice of the reference structure.

Here, we would like to emphasize that all of our conclusions involving B-factors and other nonprimary data depend on several critical assumptions. The danger of using derived data, such as B-factors, lies in the inaccuracies of the refinement processes linking the primary data from x-ray crystallography and NMR with model structures. All the structures submitted to the PDB are based on time and ensemble-average signals that undoubtedly affect the nature of the models derived from them and potentially cause different artifacts to appear (79,80). Furthermore, it is hard to tell whether the refinement has been conducted using the state-of-the-art software at the time of deposition and whether the software has been used in an optimal manner (81). For that reason, there have been several re-refinement attempts that yielded improved structural models (81–83). Until all the artifacts are fully resolved and understood, making assumptions based on the comparison of simulations and secondary or derived data can result in overinterpreted or misinterpreted conclusions (84). Nonetheless, we find the interpretation of our results to be useful for determining the <RMSD²>^1/2 of an ensemble of structures in a crystal from B-factors as long as the Eq. 1 holds, i.e., as long as the major contribution to the measured B-factors is indeed the structural heterogeneity of molecules.

Supporting Material

One table is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01738-X.