OUTCOME- AND AUXILIARY-DEPENDENT SUBSAMPLING AND ITS STATISTICAL INFERENCE

Abstract

The performance of a biomarker predicting clinical outcome is often evaluated in a large prospective study. Due to high costs associated with bioassay, investigators need to select a subset from all available patients for biomarker assessment. We consider an outcome- and auxiliary-dependent subsampling (OADS) scheme, in which the probability of selecting a patient into the subset depends on the patient’s clinical outcome and an auxiliary variable. We proposed a semiparametric empirical likelihood method to estimate the association between biomarker and clinical outcome. Asymptotic properties of the estimator are given. Simulation study shows that the proposed method outperforms alternative methods.

1. INTRODUCTION

In medical research, there is a growing need to assess the utility of a biomarker (e.g., genetic, molecular, or imaging) in predicting disease prognosis and treatment efficacy. Such a task involves estimating the association between clinical outcome and biomarker while adjusting for confounding variables in regression models. In many cases, due to a low prevalence rate of subjects with positive outcome (e.g., response) and a low prevalence rate of positive biomarker (e.g., genetic mutations), rigorous evaluation of biomarkers performance requires large prospective cohort study. If the biomarker assays are expensive, the cost of assessing all subjects in the entire study cohort is prohibitive. In such a situation, subsampling a subset of subjects from the study cohort for biomarker assays is often necessary.

We illustrate the idea using a lung cancer biomarker study. The epidermal growth factor receptor (EGFR) inhibitors, such as Erlotinib and Gefitinib, modestly extended survival for patients with advanced non-small-cell lung cancer. Of these patients, however, researchers found that those with EGFR mutations responded to the EGFR inhibitor drugs significantly better than those without mutations. Since this finding is based on small retrospective studies, a national consortium was recently established (Eberhard et al., 2008) to prospectively evaluate EGFR mutations as a predictive biomarker for receiving EGFR inhibitors. Hundreds of patients treated with EGFR inhibitors will be assembled into a study cohort and all of them are required to submit tissue samples. The study cohort is expected to predominantly consist of non-responders to the treatment (~70%) and EGFR wild types (~85%). Due to the high cost of genotyping EGFR genes, it is not cost-effective to genotype all banked samples for such a large cohort. How to efficiently select a subset of patients for EGFR mutations assays becomes an important issue. Paez et al. (2004) found that women, East Asians, nonsmokers, and patients with adenocarcinoma have much higher probability of being EGFR mutants. Taking advantage of this finding, CALGB investigators (Jänne et al., 2008) suggested a subsampling scheme that includes a simple random subsample from the study cohort as well as two supplementary samples. Of the two supplementary subsamples, one includes all responders and the other includes nonresponders with a >0.70 likelihood score of EGFR mutations. The likelihood score of EGFR mutations is the predicted probability of a patient having EGFR mutations from logistic regression model using baseline patient predictors, such as smoking history, sex, race, and histology. The likelihood score correlates with the true status of EGFR mutations, and it contains valuable auxiliary information about EGFR mutations for those subjects who have no EGFR mutations measured.

In the preceding example, the selection of a patient into the subset depends on the outcome (tumor response: yes vs. no) and an auxiliary variable (the likelihood of EGFR mutations: likely vs. unlikely). We refer to such subsampling scheme as the outcome- and auxiliary-dependent subsampling (OADS). The OADS can be considered as an extension of the outcome-dependent subsampling (ODS). In the ODS, the subsampling depends on the subjects’ outcomes in order to enrich the selected sample with those who have a rare outcome. Study designs using the ODS subsampling have been discussed by Zhou and his colleagues (Weaver and Zhou, 2005; Zhou and Weaver, 2001; Zhou et al., 2002, 2007). In the OADS, the subsampling depends on both the subjects’ outcome and an auxiliary variable. The motivation is to achieve higher efficiency by concentrating more information in the OADS subsample as compared to the simple random subsample (SRS) and the ODS subsample. Wang and Zhou (2006) considered an OADS design with two sampling components—a random sample (SRS) and an outcome- and auxiliary-dependent sample (OADS), in which all subjects have all variables observed, including the expensive biomarker. On the other hand, the OADS design that we consider here consists of three sampling components: a simple random subsample (SRS), an outcome- and auxiliary-dependent subsample (OADS), and those subjects who are not selected. In this article, we assume that complete data information is observed for each subject in SRS and OADS. We also assume that the outcome and the auxiliary variable are observed for the rest of subjects in the study cohort.

The origin of the ODS sampling can be found in the case-control study (e.g., Breslow and Day, 1993) and its extensions such as the nested case-control study (Breslow and Cain, 1988), case-cohort study (Prentice, 1986), and two-stage study (e.g., Breslow and Chatterjee, 1999; Weinberg and Wacholder, 1993; White, 1982). These designs may be considered as examples of ODS sampling. The sampling scheme we consider in this article is closely related to a two-stage study, in which the outcomes and some stratification variables of all subjects are observed at the first stage, but the expensive biomarker and other variables are observed in a subsample of all subjects at the second stage. In a general framework of a two-stage sampling, Weaver and Zhou (2005) developed an estimated likelihood method to allow both continuous outcome and ODS subsampling. For the two-stage study with binary outcome, Flanders and Greenland (1991) and Zhao and Lipsitz (1992) proposed a Horvitz–Thompson type method (Horvitz and Thompson, 1952) that weights the complete data observed inversely with the selection probability; Breslow and Cain (1988) developed a conditional likelihood estimator; Wild (1991), Cosslett (1981), and Breslow and Holubkov (1997) studied nonparametric maximum likelihood estimation. The two-stage sampling scheme can be viewed as a missing data problem, where some subjects have the biomarker of interest missing by design in our example. In this case, the missingness is missing at random (MAR) as defined by Little and Rubin (1987). Robins et al. (1994) proposed a class of semiparametric estimators based on the inverse selection probability weighted estimating equations for the missing covariates problem. These statistical methods were proposed without considering the role of auxiliary variable, and many of these methods are not fully likelihood-based. Therefore, they may not be ideal methods for data arising from the motivating lung cancer biomarker study.

To make unbiased inference on data arising from the ODS design or the OADS design, one generally needs statistical methods that account for the outcome-dependent nature of the sampling scheme. In this article, we study statistical inference on the OADS design that consists of three sampling components: a simple random subsample (SRS), an outcome- and auxiliary-dependent subsample (OADS), and those subjects who are not selected. We formulate the association between biomarker and clinical outcome in a generalized linear model. We use an empirical likelihood method (Owen, 1988, 1990; Qin and Lawless, 1994) to enforce the constraints existing among different quantities of the observed likelihood and to estimate the conditional distribution of the covariates G(x | w). The proposed method is efficient because it involves a fully likelihood-based estimator. The proposed method is semiparametric in the sense that it treats G(x | w) as nuisance and profiles the quantity out from the likelihood function using a nonparametric procedure.

We organize the rest of the article as follows. In section 2, we specify the data structure and the likelihood function of the OADS design. In section 3, we propose a semiparametric empirical likelihood estimation method and present the asymptotic properties of the proposed estimator. In section 4, we compare via simulation the proposed method to several alternative methods and investigate the effect of the correlation between the biomarker and its auxiliary variable on estimation efficiency. A data example is provided in section 5 to illustrate the proposed method. The Appendix gives a proof outline for the asymptotic properties of the proposed estimator.

2. DATA STRUCTURE AND LIKELIHOOD

Let Y be a categorical outcome with possible values 1, …, J. Let X₁ be the biomarker of interest (continuous or binary). X₁ is observed only if a subject is selected into either the SRS subsample or the OADS subsample. Let X₂, …, X_p be additional covariates. Denote by X the covariate vector, i.e., X = {1, X₁, X₂, …, X_p} where 1 represents the intercept. X may contain both continuous and discrete variables. Let P(Y | X) be the conditional density of Y given X, which can be parameterized as a generalized linear model P_β(Y | X) = r(X′β) with r⁻¹ a known link function and β the regression parameters for X.

Let W be a categorical auxiliary variable for X₁ with possible values 1, …, K. Assume {Y, W} partitions the entire study cohort into J × K strata such that the number of subjects for the {Y = j, W = k} stratum is N_jk. Following the motivating study, we first draw an SRS subsample from the study cohort, and then from the rest of study cohort we draw an OADS subsample from each of the strata {Y = j, W = k} with j = 1, …, J and k = 1, …, K. Denote the SRS subsample by V₀, the OADS subsample by V₁ and the rest of subjects by V̄. Define V = V₀ + V₁. Let V_0jk, V_1jk, V_jk and V̄_jk denote the {Y = j, W = k} substrata for V₀, V₁, V, and V̄ respectively, and n_0jk, n_1jk, n_jk, and n̄_jk for their sizes. Notice that n_jk = n_0jk + n_1jk, where n_1jk is fixed by design, and n̄_jk = N_jk − n_jk. The data structure is as follows:

$$\begin{array}{l}\text{The}\text{SRS}\text{subsample}:\{Y_i,{\mathbf{X}}_i,W_i\}\text{for}i\in V_0\\ \text{The}\text{OADS}\text{subsample}:\{{\mathbf{X}}_i\mid Y_i,W_i\},\text{for}i\in V_1\\ \text{Subjects}\text{not}\text{in}\text{SRS}\text{or}\text{OADS}\left\{{\overline{n}}_{jk}=\sum _{i}I(Y_i=j,W_i=k)\right\},\text{for}i\in \overline{V}\end{array}$$

The combined likelihood consists of the contribution from the observed data of subjects in V₀, V₁, and V̄. Since the N − n₀ observations left in the cohort after the SRS subsample is drawn still constitute a random sample from the joint distribution of {Y, W}, {N_jk − n_0jk} must be distributed according to a multinomial distribution. Therefore, the distribution of {n̄_jk} must be the same as that of {N_jk − n_0jk}, shifted with respect to the value {n_1jk}. By putting the three parts together and by applying Bayes law to P(X | Y, W), we have the combined likelihood

$$L(\theta ,G(\mathbf{x}\mid w))=\left\{\prod _{i\in V}{P}_{\beta }(y_i\mid {\mathbf{x}}_i)\right\}\left\{\prod _{i\in V}g({\mathbf{x}}_i\mid w_i)\right\}\left\{\prod _{k=1}^K\prod _{j=1}^J{\pi }_{jk}^{{\overline{n}}_{jk}}\right\}$$ (1)

where π_jk needs to satisfy the constraint

$${\pi }_{jk}\equiv P(y=j\mid w=k)=\int P(y=j\mid \mathbf{x};\beta )dG(\mathbf{x}\mid w=k)$$ (2)

where G(x | w) is the cumulative distribution of X given W. We assume P(Y | X, W) = P_β(Y | X), which is true when W is a surrogate for X or when W is absorbed by X.

3. SEMIPARAMETRIC EMPIRICAL LIKELIHOOD METHOD

Because the constraint (2) involves G(x | w = k), inference about β requires estimation on G(x | w). One straightforward approach is fitting a parametric model to G(x | w), but β̂ inconsistency could be resulted if G(x | w = k) is misspecified, specifically when x is high-dimensional. In this section, we describe a semiparametric empirical likelihood based method that allows the maximization of the likelihood function (1) with respect to β without specifying G(x | w).

3.1. The Proposed Method

For simplicity of presentation, we assume Y = {1, 2} a binary variable with 1 for positive and 2 for negative outcome, and W = {1, 2} a binary auxiliary variable. P_β(y | x) is parameterized as a generalized linear model with a known link function, such as logit, probit, or log-log. Let $V_k={\sum }_{j=1}^2{V}_{jk}$ with size $n_k={\sum }_{j=1}^2{n}_{jk}$. Note $V={\sum }_{k=1}^2{V}_k={\sum }_{j=1}^2{\sum }_{k=1}^2{V}_{jk}$. The log of the combined likelihood (1) becomes

$$l(\theta ,G(\mathbf{x}\mid w))=\sum _{i\in V}log{P}_{\beta }(y_i\mid {\mathbf{x}}_i)+\sum _{k=1}^2\sum _{i\in V_k}log{p}_{ik}+\sum _{k=1}^2\sum _{j=1}^2{\overline{n}}_{jk}log{\pi }_{jk}$$ (3)

where p_ik = g(x_i | w_i = k) and θ = (β′, π₁₁, π₁₂)′ with π_2k = 1 − π_1k.

To estimate θ, we first profile the likelihood function l(θ, G(x | w)) in Eq. (3) by fixing θ and obtaining the empirical likelihood function of G(x | w) over all distributions whose support contains the observed x values. We then maximize the resulting profile likelihood function with respect to θ. Specifically, to maximize G(x | w) over all distributions whose support contains the observed x values, we only need to consider discrete distributions with jumps at each of the observed points (Owen, 1988, 1990; Qin and Lawless, 1994). As a result, we search for p_ik that maximize L(θ, G(x | w)) under the following constraints:

$$\left\{p_{ik}\ge 0,\sum _{i\in V_k}{p}_{ik}=1,\sum _{i\in V_k}{p}_{ik}P(y=1\mid {\mathbf{x}}_i;\beta )={\pi }_{1k}\right\},k=1,2$$ (4)

For a fixed θ, a unique maximum p_ik which satisfies the above constraints exists if 0 is inside the convex hull formed by the points {P(y = 1 | x_i; β) − π_1k} for i ∈ V_k.

Let l_N (θ) be the maximum value of the log likelihood with respect to p_ik, where p_ik and θ now satisfy the constraints (4). An explicit expression for l_N (θ) can be derived by a Lagrange multiplier argument:

$$\begin{array}{l}H(p_{ik},\theta )=\sum _{i\in V}log{P}_{\beta }(y_i\mid {\mathbf{x}}_i)+\sum _{k=1}^2\sum _{i\in V_k}log{p}_{ik}+\sum _{k=1}^2\sum _{j=1}^2{\overline{n}}_{jk}log{\pi }_{jk}\\ +\sum _{k=1}^2{t}_k\left(1-\sum _{i\in V_k}{p}_{ik}\right)+\sum _{k=1}^2{\lambda }_k\sum _{i\in V_k}{p}_{ik}({\pi }_{1k}-P(y=1\mid {\mathbf{x}}_i;\beta )),\end{array}$$

where λ_k and t_k are Lagrange multipliers. Taking derivatives with respect to p_ik, and setting $\frac{\partial H}{\partial p_{ik}}=0$ and ${\sum }_{i\in V_k}{p}_{ik}\frac{\partial H}{\partial p_{ik}}=0$, we have

$$t_k=n_k,p_{ik}=\frac{1}{n_k}\frac{1}{1+{\lambda }_k(P(y=1\mid {\mathbf{x}}_i;\beta )-{\pi }_{1k})}$$

with restriction

$$\frac{1}{n_k}\sum _{i\in V_k}\frac{P(y=1\mid {\mathbf{x}}_i;\beta )-{\pi }_{1k}}{1+{\lambda }_k(P(y=1\mid {\mathbf{x}}_i;\beta )-{\pi }_{1k})}=0$$ (5)

where λ_k and θ satisfy the constraint (5).

Typically, the true value of the Lagrange multiplier is zero. However, due to the nature of the biased sampling schemes, the λ_k are not centered at zero. To be consistent with the literature of empirical likelihood theory, we center them by reparameterizing λ_k as follows

$${\nu }_k={\lambda }_k+\frac{{\overline{n}}_{1k}/n_k}{{\pi }_{1k}}-\frac{{\overline{n}}_{2k}/n_k}{1-{\pi }_{1k}},k=1,2$$

such that ν_k has a true value 0. Now we write p_ik as

$$p_{ik}=\frac{1}{n_k}\frac{1/S_k({\mathbf{x}}_i,\theta )}{1+{\nu }_k{h}_k({\mathbf{x}}_i,\theta )}$$

and the constraint (5) as

$$\frac{1}{n_k}\sum _{i\in V_k}\frac{h_k({\mathbf{x}}_i,\theta )}{1+{\nu }_k{h}_k({\mathbf{x}}_i,\theta )}=0$$ (6)

where

$$\begin{array}{l}{h}_k({\mathbf{x}}_i,\theta )=\frac{P(y=1\mid {\mathbf{x}}_i;\beta )-{\pi }_{1k}}{S_k({\mathbf{x}}_i,\theta )},\\ S_k({\mathbf{x}}_i,\theta )=\frac{N_k}{n_k}-\frac{{\overline{n}}_{1k}/n_k}{{\pi }_{1k}}P(y=1\mid {\mathbf{x}}_i;\beta )-\frac{{\overline{n}}_{2k}/n_k}{1-{\pi }_{1k}}P(y=2\mid {\mathbf{x}}_i;\beta )\end{array}$$

Substituting p_ik into the likelihood (3), we obtain the log empirical profile likelihood

$$\begin{array}{l}{l}_N(\theta )=\sum _{i\in V}log{P}_{\beta }(y_i\mid {\mathbf{x}}_i)-\sum _{k=1}^K\sum _{i\in V_k}log{S}_k({\mathbf{x}}_i,\theta )+\sum _{k=1}^K\sum _{j=1}^2{\overline{n}}_{jk}log{\pi }_{jk}\\ -\sum _{k=1}^K\sum _{i\in V_k}log(1+{\nu }_k(\theta )h_k({\mathbf{x}}_i,y_i,\theta ))\end{array}$$ (7)

The constraint (6) implicitly defines a continuous and differentiable function ν_k(θ), and it is the same as $\frac{\partial l_N}{\partial {\nu }_k}=0$. The estimate β̂ can be obtained by solving the score equations $\frac{\partial l_N}{\partial \beta }=0,\frac{\partial l_N}{\partial \pi }=0$, and $\frac{\partial l_N}{\partial \nu }=0$. We use the Newton–Raphson iterative algorithm to solve the equations, and transform π to the logit scale to avoid the boundary problem.

3.2. Asymptotic Properties

Assume n_k/N → ρ_k, n_hk/n_k → ρ_hk, n_hjk/n_hk → ρ_hjk and all ρ’s are between 0 and 1. Note ρ_0jk ≡ π_jk. Let ξ′ = (β′, π′, ν′) be the parameter vector with dimension (p+ 2K) where dim(β) = p. Let $Q_N(\xi )=\frac{1}{N}\frac{\partial l_N(\xi )}{\partial \xi }$ be the random profile score equations with respect to ξ. Let Q(ξ) be its the limiting form so that ξ* satisfies Q(ξ) = 0.

Theorem

1. For N large enough, the score equations Q_N(ξ) = 0 at some point ξ̂ in a small neighborhood of ξ*, which is the solution of Q(ξ) = 0. Then, $\widehat{\xi }\stackrel{p}{\to }{\xi }^{\ast }$ as N → ∞.

2. Under general regularity conditions, the solution ξ̂ of Q_N(ξ) = 0 satisfies the constraint equation (6) and the score equations of l_N(θ) in (7), and

   $$\sqrt{N}(\widehat{\xi }-{\xi }^{\ast })=\sqrt{N}\left(\begin{array}{c}\widehat{\beta }-{\beta }^{\ast }\\ \widehat{\pi }-{\pi }^{\ast }\\ \widehat{\nu }-0\end{array}\right)\stackrel{d}{\to }N(0,\mathrm{\sum })$$

   where Σ = lim_{N → ∞} N var(ξ̂) = S⁻¹(V + A)S⁻¹ where S, V, and A are defined in Appendix.

An outline of the proof for the theorem is given in the Appendix. A consistent estimator of the covariance matrix Σ is Ŝ⁻¹ (V̂ +Â)Ŝ⁻¹, where Ŝ, V̂, and  are obtained by replacing the large sample quantities by their corresponding small sample quantities.

4. SIMULATION STUDIES

4.1. Comparison with Alternative Methods

To evaluate the proposed method β̂_SMP, we conduct simulation study to investigate its small sample behavior and compare it with alternative methods. We review the alternative methods as follows.

β̂_CS: Component stratification method treats the subsampling components as separate strata. It fits a logistic regression model to the pooled SRS and OADS data by setting a separate intercept term for each component. This may be viewed as an application of the Prentice and Pyke (1979) result for case-control data to our setting. This method is not fully likelihood-based and only works for data with binary outcome and a regression model with logit link.

β̂_SM: Wang and Zhou (2006) studied a semiparametric method for an OADS design with unknown {N_jk}. Working with the combined likelihood of the SRS component and the OADS component only, the authors applied similar empirical likelihood approach to estimate β.

β̂_WL: The weighted-likelihood method employs the Horvitz–Thompson approach to data from a two-stage study (e.g., Flanders and Greenland, 1991; Zhao and Lipsitz, 1992). The idea is to estimate ${\sum }_{i=1}^{N}logP(y_i\mid {\mathbf{x}}_i;\beta )$ by using the completely observed subjects and weighing their contributions inversely according to their selection probability into the second stage.

β̂_CL: The conditional likelihood method focuses on the conditional probability that a subject is selected into the second stage P(x_i|y = j, w = k, δ_i = 1) where δ_i is the selection indicator (Breslow and Cain, 1988). The β is estimated after factoring the likelihood into P(y = j|x_i; β) and the selection probability.

In the case of a binary outcome, we generate y = {1, 2} according to the following logistic model:

$$P(y=1\mid x_1,x_2;\beta )=\frac{exp({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2)}{1+exp({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2)}$$

where β₀ = −2.5, β₁ = 0.0 or 0.5, and β₂ = 0.5. The value of β₀ is chosen to simulate the situation of a rare disease. Under this model, β_k (k = 0, 1, 2) represents the increase in log odds ratio of observing y = 1 due to the corresponding covariate while holding other covariates fixed. Two types of distribution of X are considered: (i) $x_1=I(x_1^{\ast }>C_{90\%})$ where $x_1^{\ast }\sim N(0,1)$ and C_90% is its 90th percentile, x₂ has the same distribution as x₁, and they are independent. Define w = I(x₁ + ε > C_90%), where ε ~ N(0, 0.25), such that corr(x₁, w) = 0.64. (ii) x₁ and x₂ are independent standard normal variables. Define w = I[x₁ + ε > 0], where ε ~ N(0, 0.25), such that corr(x₁, w) = 0.82.

A simple random subsample (SRS) of size n₀ = 300 is chosen first without stratifying on w from the study cohort of 30,000. Then 50 subjects are sampled from each of the four strata defined by y and w, resulting in n₁ = 200 subjects in the OADS subsample.

Simulation is based on 2,000 independent runs. Results are displayed in Table 1 for binary x₁ and Table 2 for normal x₁ with mean of the estimates (Mean), standard deviation of the estimates (SE), mean of the estimated standard errors ( $\widehat{\text{SE}}$), and coverage of the 95% nominal confidence intervals (Coverage).

Table 1.

Simulation of logistic regression with Bernoulli X₁

		β1 = 0.0				β1 = 0.5
Methods		Mean	SE	$\widehat{\text{SE}}$	Coverage	Mean	SE	$\widehat{\text{SE}}$	Coverage
CS	β̂0	−2.53	0.24	0.23	0.95	−2.52	0.24	0.23	0.95
	β̂1	0.01	0.39	0.37	0.95	0.51	0.39	0.37	0.94
	β̂2	0.50	0.38	0.37	0.95	0.49	0.38	0.36	0.95
SM	β̂0	−2.52	0.22	0.22	0.95	−2.51	0.22	0.22	0.95
	β̂1	0.01	0.34	0.33	0.94	0.51	0.33	0.32	0.95
	β̂2	0.49	0.33	0.32	0.96	0.48	0.33	0.32	0.95
WL	β̂0	−2.51	0.06	0.06	0.94	−2.50	0.06	0.06	0.95
	β̂1	0.01	0.27	0.26	0.93	0.50	0.24	0.23	0.94
	β̂2	0.48	0.38	0.36	0.95	0.47	0.36	0.35	0.95
CL	β̂0	−2.50	0.07	0.07	0.94	−2.50	0.07	0.07	0.95
	β̂1	0.01	0.19	0.18	0.95	0.50	0.18	0.17	0.94
	β̂2	0.49	0.33	0.32	0.95	0.48	0.33	0.32	0.95
SMP	β̂0	−2.50	0.05	0.05	0.94	−2.50	0.05	0.05	0.94
	β̂1	0.00	0.11	0.11	0.96	0.50	0.10	0.10	0.96
	β̂2	0.49	0.33	0.32	0.96	0.48	0.33	0.32	0.95
ALL	β̂0	−2.50	0.03	0.02	0.94	−2.50	0.03	0.02	0.95
	β̂1	−0.00	0.07	0.07	0.95	0.50	0.06	0.06	0.95
	β̂2	0.50	0.06	0.06	0.94	0.50	0.06	0.06	0.95

Note: Assume $P(y=1\mid x_1,x_2;\beta )=\frac{exp({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2)}{1+exp({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2)}$, where β₀ = −2.5, β₁ = 0.0 or 0.5, and β₂ = 0.5. $x_1=I[x_1^{\ast }>0]$ where $x_1^{\ast }\sim N(0,1)$. x₂ ~ x₁, and they are independent. $w=I[x_1^{\ast }+\epsilon >0]$ Where ε~ N(0, 0.25).

Table 2.

Simulation of logistic regression with standard normal X₁

		β1 = 0.0				β1= 0.5
Methods		Mean	SE	$\widehat{\text{SE}}$	Coverage	Mean	SE	$\widehat{\text{SE}}$	Coverage
CS	β̂0	−2.55	0.36	0.35	0.94	−2.56	0.42	0.39	0.96
	β̂1	0.01	0.20	0.20	0.95	0.51	0.20	0.20	0.95
	β̂2	0.51	0.13	0.13	0.94	0.51	0.13	0.13	0.95
SM	β̂0	−2.53	0.22	0.22	0.95	−2.53	0.22	0.22	0.95
	β̂1	0.00	0.14	0.15	0.95	0.51	0.16	0.15	0.94
	β̂2	0.51	0.11	0.11	0.95	0.50	0.11	0.11	0.95
WL	β̂0	−2.51	0.05	0.05	0.94	−2.51	0.06	0.06	0.94
	β̂1	0.00	0.07	0.07	0.95	0.51	0.08	0.08	0.95
	β̂2	0.51	0.11	0.11	0.95	0.50	0.12	0.12	0.95
CL	β̂0	−2.51	0.05	0.05	0.94	−2.50	0.05	0.05	0.95
	β̂1	0.00	0.07	0.07	0.95	0.50	0.07	0.07	0.94
	β̂2	0.51	0.11	0.11	0.95	0.50	0.11	0.11	0.95
SMP	β̂0	−2.51	0.05	0.05	0.94	−2.50	0.05	0.05	0.95
	β̂1	0.00	0.04	0.04	0.96	0.50	0.04	0.04	0.96
	β̂2	0.51	0.11	0.11	0.95	0.50	0.11	0.11	0.96
ALL	β̂0	−2.50	0.02	0.02	0.94	−2.50	0.02	0.02	0.94
	β̂1	0.00	0.02	0.02	0.95	0.50	0.02	0.02	0.95
	β̂2	0.50	0.02	0.02	0.95	0.50	0.02	0.02	0.95

Note: Assume $P(y=1\mid x_1,x_2;\beta )=\frac{exp({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2)}{1+exp({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2)}$, where β₀ = −2.5, β₁ = 0.0 or 0.5, and β₂ = 0.5. x₁ and x₂ are sampled from independent standard normal variables; w = I[x₁ + ε > 0], where ε ~ N(0, 0.25).

We make the following observations from the two tables. First, all estimators except β̂_CS yield consistent estimates for all regression parameters β including the intercept term. Second, as shown by a smaller standard error, β̂_SM is more efficient in estimating β₁ than β̂_CS is, but the estimators β̂_WL, β̂_CL, and β̂_SMP, which incorporate the information from the N_jk, are more efficient than the estimators β̂_CS and β̂_SM, which do not utilize such information. Third, the proposed method β̂_SMP produces good estimation of var(β̂_SMP), as shown in Tables 1 and 2, by the coverage of the 95% nominal confidence intervals based on the estimated variances. As a reference, the two tables also provide the results assuming all subjects in the cohort have complete data (β̂_ALL). It can be seen that the standard errors of β̂ associated with β̂_SMP are not much bigger than those of β̂_ALL.

Based on the preceding observations, we conclude that the proposed estimator β̂_SMP performs better than alternative estimators in the analysis of the OADS design data with known N_jk. It yields more efficient estimates than the weighted likelihood method and the conditional likelihood method. The proposed variance estimator yields good coverage by the 95% nominal confidence intervals.

4.2. Impact of Auxiliary Information

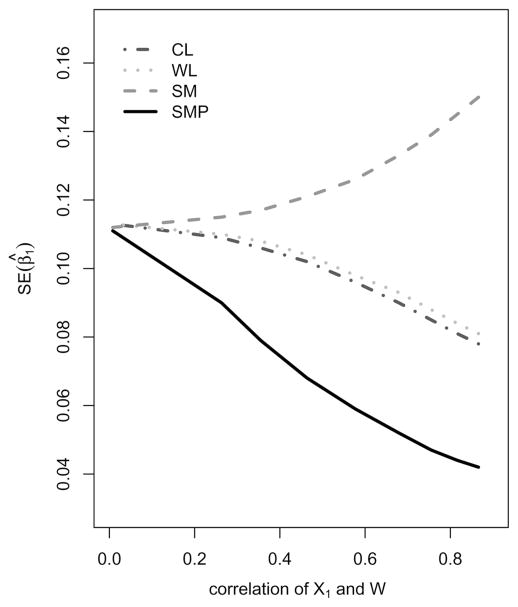
An important issue in the OADS subsampling that we discussed is the impact of the auxiliary variables on study efficiency. In particular, it is useful to examine the correlation between the biomarker and its auxiliary variable in the estimation precision of β̂₁. We only consider the case of normal distributed X₁. Through simulation, we investigate this issue by systematically changing the variance of the normally distributed random error ε such that corr(X₁, W) varies from 0.0 to 0.9 with seven intermediate values while other simulation settings remain the same. Figure 1 displays the relationship of the simulated standard deviation of β̂₁ and corr(X₁, W) for four estimators β̂_SM, β̂_WL, β̂_CL, and β̂_SMP, where each point corresponds to an average of 2,000 independent simulation runs.

Figure 1.

Estimation efficiency and corr(X₁, W). Note: The Y-axis denotes the standard error of β̂₁. The X-axis denotes the correlation between X₁ and W with X₁ ~ N(0, 1).

The significant observations from Figure 1 are as follows. As the correlation between X₁ and W increases, the standard errors of β̂₁ constantly decrease, regardless of the distribution of X₁ and the definition of W. Substantial efficiency gain, say >30% of the maximum possible gain, occurs when corr(X₁, W) is moderate, say >0.25. Importantly, if there is no correlation between X₁ and W, i.e., W contains no auxiliary information on X₁, the standard error of β̂₁ of β̂_SM and those of β̂_CL and β̂_SMP are about the same. In other words, a noninformative auxiliary variable will not improve the estimation precision of the biomarker effect, though it does improve the precision in estimating the intercept (not shown in this figure). Also, β̂_SMP appears at least as efficient as β̂_SM, β̂_WL, and β̂_CL in estimating β₁ when the auxiliary variable W is not informative on X₁.

5. DATA EXAMPLE

The motivating lung cancer biomarker study is a concept to be approved by the consortium and the data are not available for illustration. In this section, we illustrate the proposed method using a dataset from the Collaborative Perinatal Project (CPP) (Niswander and Gordon, 1972). Women who were pregnant were enrolled through university-affiliated medical clinics. In all, 55,908 pregnancies were registered, representing the experience of about 44,000 women. The children born during the study were followed for various outcomes for up to 8 years. One of the hypotheses is that the level of polychlorinated biphenyl (PCB), a pollutant, is related to performance on the Wechsler Intelligence Scale for children at 7 years of age (Longnecker et al., 2002). Because of the cost associated with the blood serum assay, the PCB level is measured for two supplemental subgroups of subjects in addition to a random sample of 1,000 subjects. Two supplemental subgroups have 200 subjects each sampled from the subgroup defined by the IQ scores that are one standard deviation above and below the mean of the cohort IQ scores.

The CPP is an ongoing study and the available dataset has 849 SRS subjects and 189 OADS subjects. The OADS subsample is selected by the outcome only in the original CPP study design. For the purpose of illustration, we resample the 849 subjects in the SRS subsample of the available dataset and form a hypothetical cohort of size 7,500. We define a binary outcome with Y = 1 if IQ is below normal and Y = 2 otherwise. We create a surrogate W for PCB by letting W = 1 if PCB + ε ≤ 6.3 and W = 2 otherwise, where 6.3 is the 75th percentile of PCB such that corr(PCB, W) = 0.44. Other covariates include race (white vs. black), socioeconomic status of the child’s family (SES), the child’s sex (female vs. male), and the mother’s education level (MEDU). Continuous variables, MEDU, SES, and PCB, are centered at their means (Table 3).

Table 3.

Data structure of the data example

Y	W	V0	V1	V̄
1	1	18	20	419
1	2	3	20	79
2	1	228	20	5483
2	2	51	20	1139
		300	80	7120

The results of analysis in Table 4 confirm previous simulation findings. The estimators β̂_WL, β̂_CL, and β̂_SMP yield more precise estimates as evidenced by their narrower 95% CIs on the odds ratio for the PCB than those from β̂_CS and β̂_SM. Further, the β̂_SMP is the most efficient among the estimators among β̂_WL, β̂_CL, and β̂_SMP, which use the cohort stratum size information. It is observed that the efficiency gain of the estimators β̂_WL, β̂_CL, and β̂_SMP over the estimators β_CS and β_SMP is only observed on the PCB effect, while the standard errors of other covariates remain unchanged since the chosen auxiliary variable is not correlated with other covariates in the model. The analysis suggests that the PCB level in the trimester blood serum specimens is not significantly related to the abnormal IQ status for child at 7 years of age. Those children who are white and have higher socioeconomic status and longer years of mother’s education have better odds of having normal or high IQ scores.

Table 4.

Analysis of the data example

Methods		β̂	SE(β̂)	OR	95% CI
CS	int	−2.726	0.390	0.066	(0.030, 0.141)
	PCB	0.035	0.074	1.036	(0.896, 1.198)
	MEDU	−0.425	0.091	0.654	(0.547, 0.781)
	SES	−0.104	0.121	0.902	(0.712, 1.142)
	RACE	−1.680	0.453	0.186	(0.077, 0.453)
	SEX	0.297	0.379	1.346	(0.640, 2.831)
SM	int	−2.469	0.344	0.085	(0.043, 0.166)
	PCB	0.045	0.051	1.046	(0.946, 1.156)
	MEDU	−0.346	0.078	0.707	(0.607, 0.824)
	SES	−0.121	0.113	0.886	(0.710, 1.106)
	RACE	−1.637	0.394	0.195	(0.090, 0.421)
	SEX	−0.045	0.334	0.956	(0.496, 1.840)
WL	int	−2.418	0.265	0.089	(0.053, 0.150)
	PCB	0.020	0.066	1.021	(0.896, 1.163)
	MEDU	−0.318	0.076	0.727	(0.626, 0.845)
	SES	−0.161	0.114	0.851	(0.681, 1.064)
	RACE	−1.570	0.411	0.208	(0.093, 0.465)
	SEX	0.012	0.345	1.012	(0.515, 1.988)
CL	int	−2.419	0.261	0.089	(0.053, 0.148)
	PCB	0.044	0.040	1.045	(0.966, 1.131)
	MEDU	−0.347	0.078	0.707	(0.606, 0.825)
	SES	−0.121	0.112	0.886	(0.711, 1.104)
	RACE	−1.637	0.393	0.195	(0.090, 0.420)
	SEX	−0.046	0.333	0.956	(0.498, 1.835)
SMP	int	−2.390	0.254	0.092	(0.056, 0.151)
	PCB	0.029	0.038	1.029	(0.955, 1.109)
	MEDU	−0.349	0.079	0.705	(0.604, 0.824)
	SES	−0.116	0.112	0.890	(0.714, 1.110)
	RACE	−1.644	0.395	0.193	(0.089, 0.419)
	SEX	−0.051	0.336	0.951	(0.492, 1.836)

Note: The outcome is below-normal IQ scores for children at 7 years of age. PCB is the effect of interest. SES is the socioeconomic status of the family; SEX and RACE are the gender and race of the child. MEDU is the mother’s education level. Continuous covariates including PCB, MEDU, and SES are centered at their means.

6. DISCUSSION

We have proposed a semiparametric empirical likelihood-based method for efficient inference on data from an outcome- and auxiliary-dependent subsampling design in which both a simple random subsample (SRS) and an outcome- and auxiliary-dependent subsample (OADS) are simultaneously observed. Adding an OADS subsample to the SRS subsample will improve the efficiency on a rare disease. One can view the design a generalization of case-cohort study and two-stage study. The advantage of the design is that when the cohort stratum size information, as defined by the outcome and the auxiliary variable, is known, we may further increase study efficiency. The proposed method is applicable to a generalized linear model with any link function for categorical outcome data. This method is robust to misspecification of the conditional distribution of the biomarker covariates, given the auxiliary variable. The proposed estimator has asymptotic normality property. Simulation supports its small sample behavior. It is superior to alternative methods. The proposed variance estimator yields a good nominal coverage by the 95% confidence interval. Simulation also suggests that the OADS design is most efficient when the correlation between the biomarker and the chosen auxiliary variable has moderate or high correlation. We illustrate the proposed method by fitting a logistic regression to a dataset from the CPP study.

Nonparametric estimation of the covariates distribution jointly with maximum likelihood estimation of β has been studied by several authors in two-stage studies (e.g., Breslow and Holubkov, 1997; Scott and Wild, 1997). In principle, these nonparametric maximum-likelihood methods can be extended to our design setting. Since our method is fully likelihood-based, the efficiency of these possible extensions are not expected better than our method. It should be pointed out that a binary outcome model with logit link is used to illustrate the subsampling scheme as well as the proposed estimator, but the approach is equally applicable to continuous outcome and linear regression model. In practice, multiple existing variables may contain auxiliary information for the biomarker of interest. More auxiliary variables mean more constraints to be used to derive the empirical likelihood-based estimator, and this may create a convergence problem in the case of small sample size. We recommend not adding auxiliary variables that lack correlation with the biomarker of interest. If multiple variables exist as candidates for auxiliary variables, a dimension reduction procedure can be used to summarize the auxiliary information. For example, in the EGFR lung caner study, we proposed to predict the EGFR mutation likelihood using a logistic regression model with these variables as predictive covariates and the predicted EGFR mutation likelihood is used as the sole auxiliary variable for stratification. It is worth noticing that auxiliary variables are used to establish the connection between the selected patients and the unselected patients. An omission of auxiliary variable may cause loss of efficiency but will not complicate the consistency of the proposed estimator. When the auxiliary variable is continuous, one has to categorize the auxiliary variable into a categorical variable before applying the proposed method. Wang and Zhou (2009) studied an estimated likelihood method in a similar sampling scheme, which utilizes the auxiliary information from a continuous variable with help from a kernel smoother. An empirical likelihood approach that handles a continuous auxiliary covariate is theoretically possible, and it will be an interesting topic for future research.

APPENDIX

The log profile score function consists of two parts:

$$\begin{array}{l}{l}_N=\sum _{h=0}^1\sum _{k=1}^2\sum _{j=1}^2\sum _{i\in V_{\mathit{hjk}}}(logP(y_i\mid x_i;\beta )-log{S}_k({\mathbf{x}}_i,\theta )-log(1+{\nu }_k{h}_k({\mathbf{x}}_i,\theta )))\\ +\sum _{k=1}^2\sum _{j=1}^2{\overline{n}}_{jk}log{\pi }_{jk}\\ \equiv l_V+l_{\overline{V}}\end{array}$$

Let ξ = (β′, π′, ν′)′ = (β′, π₁₁, π₁₂, ν₁, ν₂)′. The score equations of the profile likelihood in Eq. (7) have the form

$$\begin{array}{l}\frac{\partial l_N(\xi )}{\partial \xi }=\frac{\partial l_V(\xi )}{\partial \xi }+\frac{\partial l_{\overline{V}}}{\partial \xi }\\ =\sum _{h=0}^1\sum _{k=1}^2\sum _{j=1}^2\sum _{i\in V_{\mathit{hjk}}}\psi ({\mathbf{x}}_i,y_i,\xi )+\sum _{k=1}^2\sum _{j=1}^{2}t({\overline{n}}_{jk},{\pi }_{jk})\end{array}$$

In particular,

$$\frac{\partial l_N(\xi )}{\partial \xi }={\left(\frac{\partial l_N}{\partial {\beta }^{\prime }},\frac{\partial l_N}{\partial {\pi }_{11}},\frac{\partial l_N}{\partial {\pi }_{12}},\frac{\partial l_N}{\partial {\nu }_1},\frac{\partial l_N}{\partial {\nu }_2}\right)}^{\prime }$$

where

$$\begin{array}{l}\frac{\partial l_N(\xi )}{\partial \beta }=\sum _{h=0}^1\sum _{k=1}^2\sum _{j=1}^2\sum _{i\in V_{\mathit{hjk}}}\left[\frac{\partial P(y_i\mid {\mathbf{x}}_i;\beta )/\partial \beta }{P_{\beta }(y_i\mid {\mathbf{x}}_i)}-\frac{\partial S_k({\mathbf{x}}_i,\theta )/\partial \beta }{S_k({\mathbf{x}}_i,\theta )}-\frac{{\nu }_k\frac{\partial h_k({\mathbf{x}}_i,\theta )}{\partial \beta }}{1+{\nu }_k{h}_k({\mathbf{x}}_i,\theta )}\right]\\ \frac{\partial l_N(\xi )}{\partial {\pi }_{1k}}=-\sum _{h=0}^1\sum _{k=1}^2\sum _{j=1}^2\sum _{i\in V_{\mathit{hjk}}}\left[\frac{\partial S_k({\mathbf{x}}_i,\theta )/\partial {\pi }_{1k}}{S_k({\mathbf{x}}_i,\theta )}+\frac{{\nu }_k\frac{\partial h_k({\mathbf{x}}_i,\theta )}{\partial {\pi }_{1k}}}{1+{\nu }_k{h}_k({\mathbf{x}}_i,\theta )}\right]\\ \frac{\partial l_N}{\partial {\nu }_k}=-\sum _{h=0}^1\sum _{k=1}^2\sum _{j=1}^2\sum _{i\in V_{\mathit{hjk}}}\left[\frac{h_k({\mathbf{x}}_i,\theta )}{1+{\nu }_k{h}_k({\mathbf{x}}_i,\theta )}\right]+\frac{{\overline{n}}_{1k}}{{\pi }_{1k}}-\frac{{\overline{n}}_{2k}}{1-{\pi }_{1k}}\end{array}$$

Let h = 0, 1 with 0 corresponding to the SRS subsample V₀ and 1 corresponding to the OADS subsample V₁. When the sample size is large, n/N → ρ_V, n_k/N → ρ_k, n_hk/n_k → ρ_hk, n_hjk/n_hk → ρ_hjk, (ρ_0jk ≡ π_jk). All ρ’s are (0,1). We assume regularity conditions of maximum likelihood estimator are satisfied. The following two results are useful in our proof.

Result 1

As N_jk/N_k → π_jk and n_0jk/n_0k → π_jk, it holds

$$S_k({\mathbf{x}}_i,\theta )\stackrel{a}{=}{S}_k^{\ast }({\mathbf{x}}_i,\theta )\stackrel{a}{=}{\stackrel{\sim }{S}}_k({\mathbf{x}}_i,\theta )$$

where

$$\begin{array}{l}{S}_k({\mathbf{x}}_i,\theta )=\frac{N_k}{n_k}-\sum _{j=1}^2\frac{{\overline{n}}_{jk}/n_k}{{\pi }_{jk}}P(y=j\mid {\mathbf{x}}_i;\beta )\\ S_k^{\ast }({\mathbf{x}}_i,\theta )=\sum _{j=1}^2\frac{n_{0jk}/n_k}{{\pi }_{jk}}P(y=j\mid {\mathbf{x}}_i;\beta )+\sum _{j=1}^2\frac{n_{1jk}/n_k}{1-{\pi }_{jk}}P(y=j\mid {\mathbf{x}}_i;\beta )\end{array}$$

and

$${\stackrel{\sim }{S}}_k({\mathbf{x}}_i,\theta )={\rho }_{0k}+{\rho }_{1k}\sum _{j=1}^2\frac{{\rho }_{1jk}}{{\pi }_{jk}}P(y=j\mid {\mathbf{x}}_i;\beta )$$

And, $\stackrel{a}{=}$ means asymptotically equivalent $a_N=b_N+O_p(1/\sqrt{N})$.

Result 2

For any continuous function g(k(x, θ)), at ξ = ξ*,

$$\begin{array}{l}\frac{1}{n_k}\sum _{h=0}^1\sum _{j=1}^2\sum _{i\in V_{\mathit{hjk}}}{g}_k({\mathbf{x}}_i,\theta )\stackrel{a.s.}{\to }\sum _{h=0}^1\sum _{j=1}^2{\rho }_{jk}E[g_k(\mathbf{x},0)\mid y=j,w=k]\\ =\int g_k(\mathbf{x},\theta )\left[\sum _{h=0}^1{\rho }_{hk}\sum _{j=1}^2{\rho }_{\mathit{hjk}}\frac{P(y=j\mid \mathbf{x};\beta )}{{\pi }_{jk}}\right]d{G}_k(\mathbf{x})\\ =E[{\stackrel{\sim }{S}}_k(\mathbf{x},\theta )g_k(\mathbf{x},\theta )\mid w=k].\end{array}$$

First, we can show $\frac{1}{N}\frac{\partial l_N(\xi )}{\partial \xi }\stackrel{p}{\to }\frac{\partial {\stackrel{\sim }{l}}_N(\xi )}{\partial \xi }$ and $\frac{\partial {\stackrel{\sim }{l}}_N({\xi }^{\ast })}{\partial \xi }\stackrel{p}{\to }0$ at ξ = ξ*.

In particular,

$$\begin{array}{l}\frac{1}{N}\frac{\partial l_N}{\partial \beta }=\sum _{k=1}^2\frac{n_k}{N}\sum _{h=0}^1\frac{n_{hk}}{n_k}\sum _{j=1}^2\frac{n_{\mathit{hjk}}}{n_{hk}}\\ \times \sum _{i\in V_{\mathit{hjk}}}\frac{1}{n_{\mathit{hjk}}}\left[\frac{\partial P(y_i\mid {\mathbf{x}}_i;\beta )/\partial \beta }{P(y_i\mid {\mathbf{x}}_i;\beta )}-\frac{\partial S_k({\mathbf{x}}_i,\theta )/\partial \beta }{S_k({\mathbf{x}}_i,\theta )}-\frac{{\nu }_k\frac{\partial h_k({\mathbf{x}}_i,\theta )}{\partial \beta }}{1+{\nu }_k{h}_k({\mathbf{x}}_i,\theta )}\right]\\ \stackrel{\text{a}.\text{s}.}{\to }\sum _{k=1}^2{\rho }_k\sum _{h=0}^1{\rho }_{hk}\sum _{j=1}^2\frac{{\rho }_{\mathit{hjk}}}{{\pi }_{jk}}\int \frac{\partial P(y=j\mid \mathbf{x};\beta )}{\partial \beta }d{G}_k(\mathbf{x})\\ -\sum _{k=1}^2{\rho }_k\int \frac{\partial {\stackrel{\sim }{S}}_k({\mathbf{x}}_i,\theta )}{\partial \beta }d{G}_k(\mathbf{x})=0\\ \frac{\partial l_N}{\partial {\pi }_{1k}}=\frac{{\overline{n}}_{1k}/N}{{\pi }_{1k}}-\frac{{\overline{n}}_{2k}/N}{1-{\pi }_{1k}}-\sum _{h=0}^1\sum _{k=1}^2\sum _{j=1}^2\sum _{i\in V_{\mathit{hjk}}}\left[\frac{\partial S_k({\mathbf{x}}_i,\theta )/\partial {\pi }_{1k}}{S_k({\mathbf{x}}_i,\theta )}+\frac{{\nu }_k\frac{\partial h_k({\mathbf{x}}_i,\theta )}{\partial {\pi }_{1k}}}{1+{\nu }_k{h}_k({\mathbf{x}}_i,\theta )}\right]\\ \stackrel{\text{a}.\text{s}.}{\to }\frac{{\rho }_k{\gamma }_{1k}}{{\pi }_{1k}}-\frac{{\rho }_k{\gamma }_{2k}}{1-{\pi }_{1k}}-{\rho }_k\int \frac{\partial {\stackrel{\sim }{S}}_k(\mathbf{x},\theta )}{\partial {\pi }_{1k}}d{G}_k(\mathbf{x})=0\end{array}$$

where n̄_jk/n_k → γ_jk as n_k/N → ρ_k, N_k/N → π_k.

$$\begin{array}{l}\frac{1}{N}\frac{\partial l_N}{\partial {\nu }_k}\stackrel{\text{a}.\text{s}.}{\to }\sum _{k=1}^2{\rho }_k\sum _{h=0}^1{\rho }_{hk}\sum _{j=1}^2{\rho }_{\mathit{hjk}}\int \frac{P(y=1\mid \mathbf{x};\beta )-{\pi }_{1k}}{{\stackrel{\sim }{S}}_k(\mathbf{x},\theta )}\frac{P(y=j\mid \mathbf{x};\beta )}{{\pi }_{jk}}d{G}_k(\mathbf{x})\\ =\sum _{k=1}^2{\rho }_k\int (P(y=1\mid \mathbf{x};\beta )-{\pi }_{1k})d{G}_k(\mathbf{x})=0\end{array}$$

We can easily show that $\frac{1}{N}\frac{{\partial }^2{l}_N(\xi )}{\partial \xi \partial {\xi }^{\prime }}\stackrel{p}{\to }\frac{{\partial }^2\stackrel{\sim }{l}(\xi )}{\partial \xi \partial {\xi }^{\prime }}$ uniformly for ξ ∈ Ξ, and at the true parameter value, it is invertible. Furthermore, we have shown that $\frac{1}{N}\frac{\partial l_N({\xi }^{\ast })}{\partial \xi }\stackrel{p}{\to }0$. Clearly, $\frac{\partial l_N(\xi )}{\partial \xi }$ is a continuous function of ξ that maps Ξ into R^p+2K. Then we can apply the general version of Foutz’s consistency theorem (Foutz, 1977) to conclude that ξ̂ exists in the set Ξ with probability approaching one as N → ∞, and since the size of Ξ is arbitrarily small, that $\widehat{\xi }\stackrel{p}{\to }{\xi }^{\ast }$.

To show asymptotic normality of ξ̂ where ξ = (β′, π′, ν′)′, we consider a first-order Taylor series expansion of the profile score function around the true parameter value ξ*:

$$0=\frac{1}{N}\frac{l_N(\widehat{\xi })}{\partial \xi }=\frac{1}{N}\frac{l_N({\xi }^{\ast })}{\partial \xi }+\frac{1}{N}\frac{{\partial }^2{l}_N(\stackrel{\sim }{\xi })}{\partial \xi \partial {\xi }^{\prime }}(\widehat{\xi }-{\xi }^{\ast })+o_p(N^{-1/2})$$

where |ξ* − ξ̃| ≤ |ξ*− β̂|. To prove the asymptotic normality of $\sqrt{N}(\widehat{\xi }-{\xi }^{\ast })$, we need to study the asymptotic behavior of each term on the right-hand side.

First consider the first derivatives with respect to ξ. By the law of large numbers, we have

$$\frac{1}{N}\frac{l_N(\widehat{\xi })}{\partial \xi }=\stackrel{p}{\to }\sum _{k=1}^2{\rho }_{k}E[{\stackrel{\sim }{S}}_k(\mathbf{x},\theta ){\psi }_{jk}(\mathbf{x},y,\xi )\mid w=k]+\sum _{k=1}^2\sum _{j=1}^{2}E[t({\overline{n}}_{jk},{\pi }_{jk})]$$

When evaluated at ξ = ξ*, we have shown above $\frac{1}{N}\frac{\partial l_N(\xi )}{\partial \xi }$. Recall $\frac{1}{N}\frac{l_N(\xi )}{\partial \xi }=\frac{1}{N}\frac{l_V(\xi )}{\partial \xi }+\frac{1}{N}\frac{l_{\overline{V}}(\xi )}{\partial \xi }$. For i ∈ V_jk, the observations (y_i, x_i) are independent random draws either from the joint distribution of (Y, X, W) for i ∈ V₀ or from the joint distribution of (X | Y, W) for i ∈ V₁, and they do not depend on the random stratum size(N_jk − n_0jk). That is, $\frac{1}{N}\frac{\partial l_V({\xi }^{\ast })}{\partial \xi }$ is independent of $\frac{1}{N}\frac{\partial l_{\overline{V}}({\xi }^{\ast })}{\partial \xi }$.

By applying the central limit theorem, we have

$$\frac{1}{\sqrt{N}}\frac{\partial l_N({\xi }^{\ast })}{\partial \xi }\stackrel{d}{\to }N(0,V+A)$$

where

$$V=\underset{N\to \infty }{lim}var\left(\frac{1}{\sqrt{N}}\frac{l_V({\xi }^{\ast })}{\partial \xi }\right)={\rho }_{0}var(\psi (\mathbf{x},y,\xi ))+\sum _{k=1}^2{\rho }_k{\rho }_{1k}\sum _{j=1}^2{\rho }_{1jk}var(\psi (\mathbf{x},y,\xi ))$$

and

$$A=\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& A_{{\pi }_{11}}& 0& 0& 0\\ 0& 0& A_{{\pi }_{12}}& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right)$$

where

$$\begin{array}{l}{A}_{{\pi }_{1k}}=\underset{N\to \infty }{lim}var\left(\frac{1}{\sqrt{N}}\frac{l_{\overline{V}}({\xi }^{\ast })}{\partial {\pi }_{1k}}\right)=\underset{N\to \infty }{lim}\sum _{k=1}^2\sum _{j=1}var\left(\frac{1}{\sqrt{N}}\left(\frac{{\overline{n}}_{jk}}{{\pi }_{jk}}-\frac{{\overline{n}}_{2k}}{1-{\pi }_{1k}}\right)\right)\\ =(1-{\rho }_0){\pi }_k\left(\frac{1}{{\pi }_{1k}}+\frac{1}{1-{\pi }_{1k}}\right),\text{where}{n}_0/N\to {\rho }_0\end{array}$$

Similarly,

$$\frac{1}{N}\frac{{\partial }^2{l}_N(\xi )}{\partial \xi \partial {\xi }^{\prime }}\stackrel{p}{\to }\sum _{k=1}^2{\rho }_{k}E[{\stackrel{\sim }{S}}_k(\mathbf{x},\theta )\psi (\mathbf{x},y,\xi )]+\sum _{k=1}^2\sum _{j=1}^{2}E\left[\frac{\partial t({\overline{n}}_{jk},{\pi }_{jk})}{\xi }\right]\equiv S(\xi )$$

Since S(ξ*) is invertible, it allows us to arrange Eq. (6) as

$$\sqrt{N}(\widehat{\xi }-{\xi }^{\ast })=-{\left[\frac{1}{N}\frac{{\partial }^2{l}_N({\xi }^{\ast })}{\partial \xi \partial {\xi }^{\prime }}\right]}^{-1}\left[\frac{1}{\sqrt{N}}\frac{\partial l_N({\xi }^{\ast })}{\partial \xi }\right]+o_p(1)$$

By Slutsky’s theorem,

$$\sqrt{N}(\widehat{\xi }-{\xi }^{\ast })=\sqrt{N}\left(\begin{array}{c}\widehat{\beta }-{\beta }^{\ast }\\ \widehat{\pi }-{\pi }^{\ast }\\ \widehat{\nu }-0\end{array}\right)\stackrel{d}{\to }N(0,\mathrm{\sum })$$

where Σ = Nvar(ξ̂) = S⁻¹ (V + A)S⁻¹, which has a sandwich form.