Figure 2.
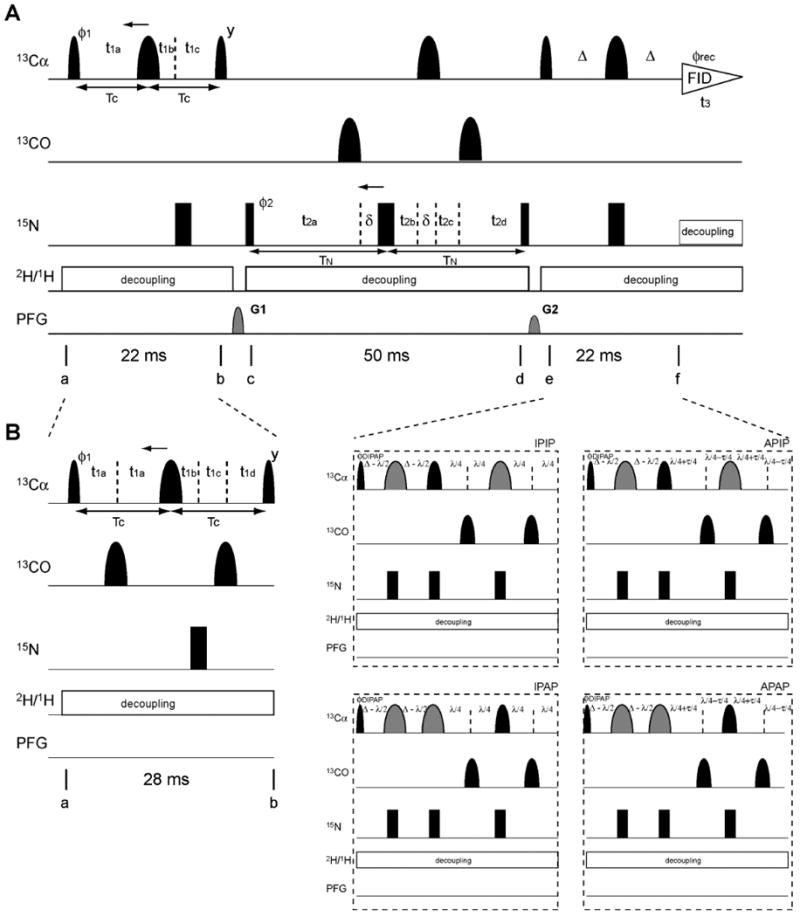
Pulse program of the 3D CANCA experiment optimized for (A) alternate and (B) uniform 13C-labeling. Narrow and wide black bars indicate non-selective π/2 and π pulses, respectively. Narrow and wide semi elliptical shapes on the carbon channel represent π/2 and π Gaussian cascades pulses (Q5 / 256 μs and Q3 / 205 μs, respectively)11 selective for the frequencies of aliphatic carbon nuclei. Wider Gaussian shapes in gray indicate Cα selective Gaussian cascades pulses (Q3 / 1557 μs). All pulses are applied along the x-axis unless otherwise indicated. (A) The delays were TC = Δ = 11 ms and TN = 25 ms, which is optimal for inter-residue connectivities. The short delay δ = 205 μs compensates for a 13C 180° pulse. The delays and increments for the 13C t1 semi-constant time (SCT) period (a-b) are: t1a = t1c = TC; t1b = 5 μs; Δt1a = -TC/n1max; Δt1c = 1/(2SWC)- TC/n1max; Δt1b = 1/(2SWC). If n1max×Δt1a < TC, a constant time (CT) is used. In this case, t1a = t1c = TC and t1b = 5 μs. Δt1a = - Δt1c = 1/(2SWC) and Δt1b = 0. The delays and increments for the 15N t2 SCT period (c-d) are: t2a = t2d = TN = 25 ms; t2b = t2c = 5 μs; Δt2a = -TN/n2max; Δt2b = Δt2d = 1/(2SWN)- TN/n2max; Δt2c = TN/n2max. If n2max×Δt2a < TN, a constant time is used. t2a = t2d = TN = 25 ms; t2b = t2c = 5 μs. Δt2a = Δt2b = Δt2d = Δt2c = 1/4(SWN). n1max and n2max are the values of the maximum Nyquist grid points in each dimension. In our experiment, both Cα and N are incremented in the SCT fashion (128 (Cα) × 128 (N) complex points, SWC = 3511 Hz, SWN = 1518 Hz). The phase cycle employed was ϕ1 = (x, -x), ϕ2 = (x, x, -x, -x), ϕrec = (y, -y, -y, y). Phase sensitive spectra in the 13C(t1) and 15N(t2) dimensions are obtained by incrementing the phases ϕ1 and ϕ2, respectively, in a States-TPPI manner12. The recycling delay is optimized based on longitudinal relaxation rates. The sine-shaped pulsed field gradients were all applied for 1.0 ms with maximum intensities of G1 = 19 G/cm (gz) and G2 = 16 G/cm (gz). Deuterium and proton decoupling are achieved by using WALTZ16 sequence (3.1 kHz and 1kHz, respectively). (B) The delays were TC = 14 ms, Δ = 11 ms and TN = 25 m, which is optimal for inter-residue connectivities. For IPAP, λ = 14.4 ms and τ = 9 ms were used. The short delay δ = 205 μs compensates for a 13C 180° pulse. The delays and increments for 13C t1 semi-CT period are: t1a = t1d = Tc/2; t1b = 3.3 ms; t1c = 3.8 ms; Δt1a = -Tc/n1max; Δt1b = 1/(2SWC)- 2TC/n1max; Δt1c = TC/n1max; δt1d = 1/(2SWC) - 2TC/n1max. If n1max×δt1a < TC, a constant time is used. t1a = t1d = Tc/2; t1b = 3.3 ms; t1c = 3.8 ms; δt1a = δt1c = δt1d = 1/4(SWC); δt1b = 0. The delays and increments for 15N t2 semi-CT or CT periods are the same as in (A). The phase cycle employed was ϕ1 = (x, -x), ϕ2 = (x, x, -x, -x), ϕDIPAP = (x, x, x, x, -x, -x, -x, -x) for IPIP and APAP, (-y, -y, -y, -y, y, y, y, y) for APIP, and (y, y, y, y, -y, -y, -y, -y) for IPAP, ϕrec = (x, -x, -x, x, -x, x, x, -x). Phase sensitive spectra in the 13C(t1) and 15N(t2) dimensions are obtained by incrementing the phases ϕ1 and ϕ2, respectively, in a States-TPPI manner. The recycling delay, pulsed-field gradients, deuterium and proton decoupling were the same as in (A).
