Two-State Reactivity Model Explains Unusual Kinetic Isotope Effect Patterns in C-H Bond Cleavage by Nonheme Oxoiron(IV) Complexes

The surging field of nonheme iron chemistry has led to the identification of a variety of iron(IV)-oxo intermediates, which perform oxidative processes such as H-abstraction and oxo-transfer reactions to a variety of molecules.[1–3] The advent of both enzymatic and synthetic examples has revealed in turn some puzzles of fundamental importance in mechanistic bioinorganic chemistry. Thus, whereas the known enzymatic species, e.g., in taurine/α-ketoglutarate dioxygenase (TauD),[4] have been shown by Mössbauer analyses to possess a ground state with a quintet spin (Q) quantum number (S = 2), all except one of the synthetic iron-oxo species have been shown by experimental means to possess triplet (T) ground states (S = 1) and low-lying quintet states.[2,3] Nevertheless, some of the reactivity patterns of the enzymatic and synthetic reagents are still similar. For example, use of deuterated taurine in reactions with TauD has revealed a kinetic isotope effect (KIE) of ∼37 for the decay of the iron-oxo species.[4,5] The synthetic compounds [Fe^IV(O)(N4Py)]²⁺ (1) and [Fe^IV(O)(BnTPEN)]²⁺(2),[6,7] despite possessing triplet ground states, also exhibit large KIE values (>30) in hydrogen abstraction (H-abstraction) from ethylbenzene vs. ethylbenzene-d₁₀.[6] A primary isotope effect supports a rate determining C-H bond cleavage. Furthermore, the observation of such large KIEs for both the enzymatic and model system reactions suggests that the reactivity of 1 and 2 is analogous to the enzyme, namely, that the excited quintet states of 1 and 2 must somehow be involved in the C-H activation.[2,3] If this is indeed the case, the reactions of the synthetic reagents should involve two-state reactivity (TSR),[8] whereby both the triplet and quintet states contribute to the overall bond activation. Subsequent calculations[9] indeed showed the probable involvement of TSR, since the excited quintet state lies close to the triplet ground state and the triplet surface eventually crosses over to the quintet surface as the reaction progressed.

The insight provided by the TSR model was utilized recently to rationalize the counterintuitive results observed when the series of [Fe^IV(O)TMC(X)]^z+ reagents (with X = acetonitrile (MeCN), trifluoroacetate (TF), azide (N₃), or thiolate (SR)) led to opposing reactivity trends in H-atom abtraction vs. oxo-transfer reactions.[10] A systematic study of the series demonstrated that the oxo-transfer capability of [Fe^IV(O)TMC(X)]^z+ towards PPh₃ increased in the order X = SR < N₃ < TF < MeCN, but the reactivity in hydrogen-atom abstraction (H-abstraction) from 9,10-dihydroanthracene (DHA) decreased in the order L = SR > N₃ > TF > MeCN, which is in the opposite direction. Thus the [Fe^IV(O)TMC(X)]^z+ oxidant exhibited a dichotomic reactivity pattern: in the oxo-transfer series it behaved as an electrophile whereby electron-releasing anionic ligands X diminished the oxidative reactivity, whereas in the C-H activation series the best H-abstractor was the poorest oxidant with X = SR. The TSR concepts showed that the involvement of the quintet state in the reaction is the root cause of these unusual reactivity patterns. Further validation of the TSR model was obtained from a more recent study on the corresponding [Ru^IV(O)TMC(X)]^z+ oxidants, where the quintet state is too high to be able to participate in the reaction;[11] this study revealed that the two reaction series exhibit precisely the same trends, indicative of the sole involvement of the triplet state.

Is it possible to interrogate more directly the TSR concept by experimental means? A set of criteria has been suggested that could be used to probe the feasibility of a TSR system.[9a, 10b] It was hypothesized that the crossover from triplet to quintet provides a tunnelling-like pathway that may be probed by an investigation of KIEs. Thus, the TSR model predicts that triplet processes will exhibit nearly classical values for k_H/k_D. For the quintet process, or in a process where spin-crossover from triplet to quintet occurs, values for k_H/k_D typical of a tunnelling mechanism were predicted. However, the critical prediction was that the KIE should vary with the strength of the C-H bond between the classical (ca. <7) and nonclassical (≫7) limits. Testing this working hypothesis is the primary goal of this paper, which reports a study of hydrocarbon oxidation by 1 and 2. Our results serve as a demonstration of the complementary roles that experiment and theory can play in a mechanistic investigation.

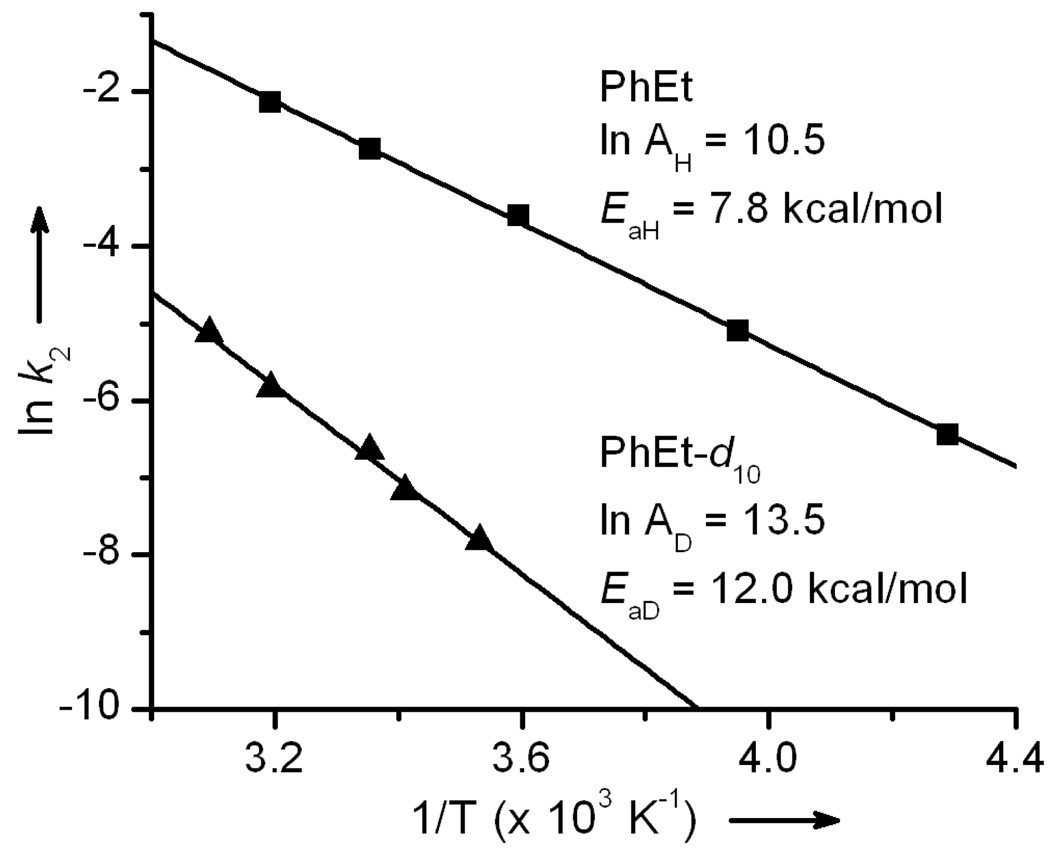
Experimental studies

Previous studies on the reactions of 1 and 2 with ethylbenzene (PhEt) and PhEt-d₁₀ showed high, non-classical k_H/k_D values of 30 and 50 for reactions performed at 25 °C.[6] KIEs of this magnitude are often associated with a mechanism involving hydrogen atom tunnelling. However, there are more stringent criteria to invoke a tunnelling model, which may be established from an evaluation of the temperature dependence of the reaction rates by analysis of their Arrhenius plots. Features representative of a reaction involving hydrogen atom tunnelling include: a difference in energies of activation (E_aH – E_aD) for the systems greater than the zero-point energy differences (ΔZPE) of the reactant C-H and C-D bonds and a ratio of the Arrhenius pre-factors yielding A_H/A_D < 0.7.[12,13] Figure 1 shows the temperature dependences of the rates of the reaction of 2 with PhEt from −40 °C to 40 °C and the reaction of 2 with PhEt-d₁₀ over the range of 10 °C to 50 °C. From these plots, it can de deduced that the KIE increases significantly from a value of 40 at 40 °C to a value of 400 at −40 °C. From the temperature dependence plots can be obtained E_a values of 7.8 (3) and 12.0 (1) kcal/mol for the oxidations of PhEt and PhEt-d₁₀ by 2, corresponding to a ΔE_a of 4.2 kcal/mol. The ΔZPE for the benzylic hydrogen and deuterium atoms of PhEt can be obtained from vibrational data, which shows a downshift of ∼800 cm⁻¹ upon deuterium substitution, corresponding to an energy difference of 2 kcal/mol. Therefore, ΔE_a > ΔZPE. Additionally, the Arrhenius plots give an A_H/A_D ratio of 0.03, a value much lower than 0.7 and in line with enzymatic systems shown to involve hydrogen-atom tunnelling.[13] Thus, the reaction of 2 with PhEt exhibits all the necessary and sufficient characteristics expected for a reaction involving H-atom tunnelling. The numbers obtained here for 2 are comparable to those recently reported by Newcomb on the temperature dependence of the KIE’s for the oxidation of benzyl alcohol by [Fe^IV(O)(TMP•)(ClO₄)] (TMP = tetramesitylporphinate dianion), which range from 28 at 23 °C to 360 at −30 °C (ΔE_a = 7 kcal/mol; A_H/A_D = 0.025 (ln A_H = 8.6 and ln A_D = 4.9)). [14]

Figure 1.

Temperature dependence of the rate constants for the reactions of 2 with PhEt (squares) and PhEt -d₁₀ (triangles).

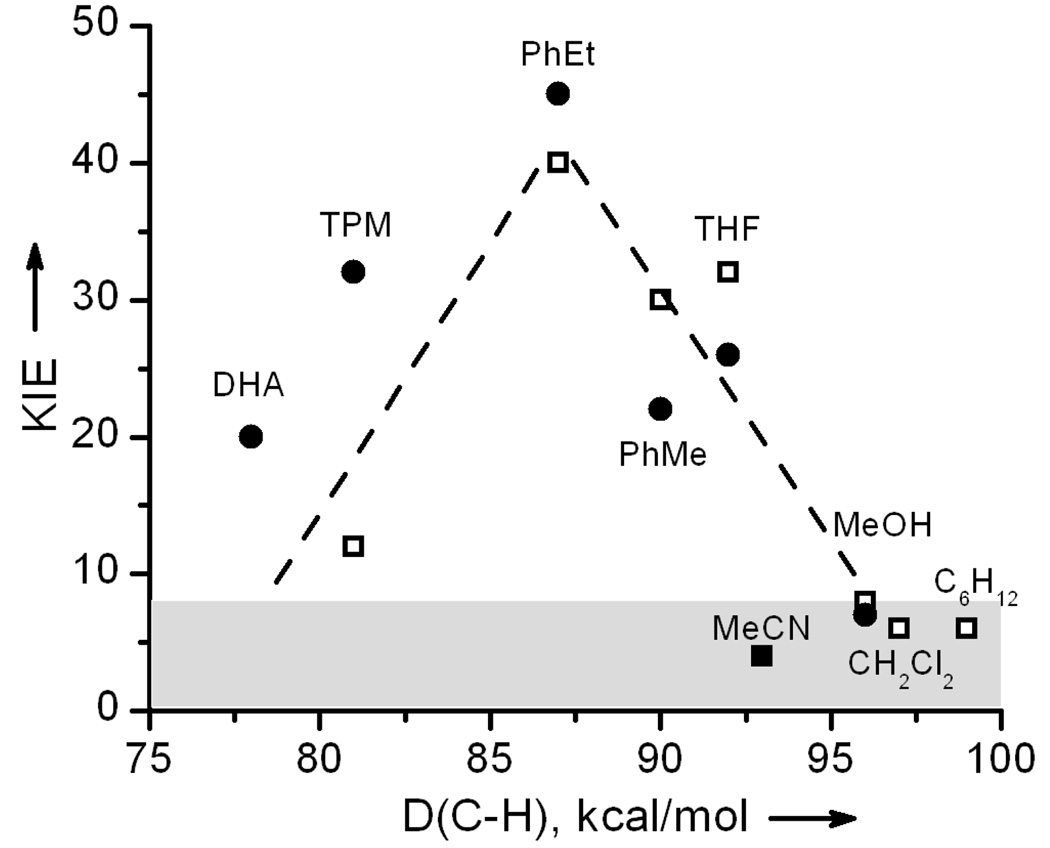
A determination of the KIEs for the oxidation by 1 and 2 of a series of substrates with a range of C-H bond dissociation energies (D(C-H)) revealed a rather surprising pattern (Figure 2). These experiments were carried out at 40 °C to shorten reaction times. For substrates with D(C-H) < 93 kcal/mol like dihydroanthracene (DHA), Ph₃CH (TPM), toluene (PhMe), and THF, the KIE values are nonclassical, as found earlier for PhEt,[6] while the KIEs for substrates with stronger C-H bonds such as MeOH, CH₂Cl₂, and C₆H₁₂ were smaller (4–8) and fell into the classical range. A value of 4 was found as well for the slow decay of 2 in MeCN and MeCN-d₃ solvent. This unusual dependence of KIE on D(C-H) is unique.

Figure 2.

Plot of KIE values vs D(C-H) for 1 (filled circles) and 2 (open squares). The filled square represents the KIE value for MeCN as estimated from the t_1/2 of 2 in MeCN and MeCN-d₃. The shaded area represents KIE values within the semiclassical limit, while the dashed lines highlight the rising and falling trends of the KIEs as a function of C-H bond dissociation energy.

A potentially similar relationship has been reported in only one other system capable of H-atom abstraction.[15] The reaction of the phthalimide N-oxyl radical (PINO) with a similar set of substrates also showed a dependence of KIE on D(C-H) with values of 11–13 for the weaker C-H bonds of benzhydrol and fluorene and values of 24–27 for the stronger C-H bonds of ethylbenzene, toluene and cyclohexane. Indeed the maximum KIE was observed when the overall reaction free-energy change was close to zero, as expected by the classical Melander-Westheimer explanation for the variation of semiclassical KIE with free energy changes during H-abstraction.[16] However, in the cases of the reactions of 1 and 2 with substrates, the reactions are all exothermic, and this same principle cannot be applied. Furthermore, the large KIE values observed for the reactions of 1 and 2 are for the substrates having weaker C-H bonds, and hence more exothermic reactions. This behaviour is clearly not what one expects from semiclassical trends in KIE; we therefore turned to calculations to provide a way to rationalize the D(C-H) dependence of KIE for 1 and 2.

Theoretical calculations: What kind of tunnelling do we expect?

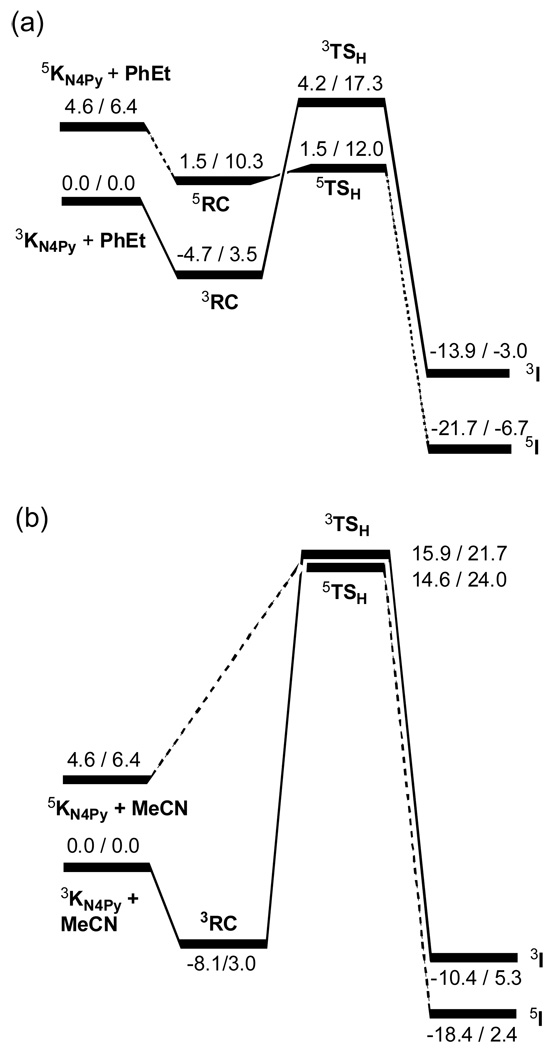
Since the reactions of PhEt figure prominently in the KIE plots above, we calculated this reaction with 1, at the common level used for the cases in previous studies, namely B3LYP/B1 (B1 is LACVP) for characterizing the C-H activation mechanism. The energy was corrected using a larger basis set, B2 (B2 is LACV3P++**), and solvent corrections (using the solvent parameters for CH₃CN). Like all previous cases,[9,10] here too we found a two-state-reactivity (TSR) scenario (see Figure 3 later); the details are given in the supporting information (SI) document.

Figure 3.

Energy profiles for the reactions of 1 (labelled as K) with ethylbenzene (PhEt) in (a) and acetonitrile (MeCN)[9b] in (b). The relative energies (in kcal/mol) of each species correspond to the B2//B1+ZPE gas phase value followed by a solvent corrected value B2//B1+ZPE +solv. The RC is a cluster of the reactants, which is stable only in the gas phase. ^2S+1I corresponds to the Fe(III)OH/R• intermediate with triplet or quintet spin.

The semiclassical KIE values calculated for the H-abstraction reactions of 1 and 2 with different hydrocarbon substrates are listed in Table 1. It is seen that the semiclassical values on the triplet surface are generally larger than those on the quintet surface. For each spin manifold, the smallest values are calculated for the substrates with the weakest C-H bond, namely PhEt and then PhMe. The quintet state KIE(Q) values for PhEt and PhMe are only slightly larger than 1. Small tunnelling corrections based on Wigner’s formula do not change these trends and do not affect the KIE(Q) values for PhEt and PhMe at all (see SI). Similar results were obtained by de Visser for the C-H activation by the model iron-oxo species of TauD.[17] Importantly, the only semiclassical values that seem to match the experimental ones are those for the substrates with the stronger C-H bonds, C₆H₁₂ and MeCN. Otherwise, the calculated KIEs show the expected trend[18] from semiclassical values, namely generally larger KIEs for higher barriers and stronger C-H bonds (e.g., compare the value for C₆H₁₂ vs PhEt). Thus, the very small KIE(Q) values are in line with the very small barriers on the quintet surface, and the larger KIE(T) values are in line with the larger triplet barriers.[18] Clearly, however, these semiclassical values in Table 1 account for neither the trends nor the very large KIE values in Figure 2 above. Furthermore, the very small semiclassical KIE(Q) values are in clear disagreement with the experimental KIE(Q) value (>37) for TauD, for which the oxoiron(IV) oxidant has a quintet ground state[4] that is responsible for the C-H bond activation.[17]

Table 1.

Semiclassical KIEs Calculated with DFT (B3LYP/B1)

Reaction [a]	KIE(T) [b]	KIE(Q) [b]	Observed KIE at 40 °C for 1 (2) [c]
KN4Py + C6H12	6.8	1.9
KN4Py + PhMe	5.9	1.4	22 (30)
KN4Py + MeCN	6.7	5.4	(4)
KN4Py + PhEt	6.3	1.4	45 (40)
KBn-TPEN + C6H12	6.8	2.7	(6)

^[a]C₆H₁₂ = cyclohexane, PhMe = toluene, MeCN = acetonitrile, PhEt = ethylbenzene. Calculations at the B3LYP/LACVP level. KIEs were calculated using the free energy difference between ^3.5TS_H and ^3,5R (^3,5K_N4Py + substrate). The reacting H atom was replaced by D.

^[b]Semiclassical values.

^[c]KIE values determined at 40 °C in MeCN-d₃ solvent, except for MeCN, which was obtained from the t_1/2 values of 2 in MeCN and MeCN-d₃ solvent.

The experimental data in Figure 2 clearly correspond to a tunneling situation, but to what kind of tunneling? Traditional tunneling through a single barrier is generally expected to be more efficient as the barrier gets narrower and to occur through the thinner part of the barrier.[19,20] Assuming that the area under the barrier is conserved in a series of substrates reacting with the same iron-oxo reagent, then larger H-abstraction barriers will have thinner cross-sections than smaller ones. Thus, under this assumption, in a tunneling via a single barrier one can arguably expect the tunneling to increase as the barrier increases. Since the H-abstraction barrier is known to increase as the C-H bond strength increases,[6,21] one might have expected that the KIE tunnelling-value will increase as the C-H bond becomes stronger. This is manifested in the left hand branch of Figure 2, but is not true for the right hand branch of the data set; here, the largest KIE value is observed for PhEt with the weakest C-H bond, and normal semiclassical-type values are measured for the substrates with strongest C-H bonds.

To formulate a possible tunnelling scenario that can serve as a working hypothesis, we display in Figure 3 the energy profiles for two extreme cases, the reactions of [Fe^IV(O)(N4Py)]²⁺ with PhEt and MeCN. Inspection of the gas phase energetics (the left hand data in each pair) shows that, in each case, the triplet surface starts as the ground state but is being crossed over by the quintet state. The triplet energy profiles in both cases are much steeper than the quintet profiles, but the barriers for H-abstraction from MeCN are considerably higher than those from PhEt, in accord with experimental data.

Since the triplet barrier in Figure 3 is generally higher than the quintet barrier, then the crossing of the quintet surface through the triplet barrier could afford a mechanism that behaves like tunnelling.[9a,10b] However, as shown in Figure 3 this mechanism depends strongly on the substrate. Thus, in the case of MeCN, the quintet energy profile itself is quite steep even in the gas phase, while in the case of PhEt the quintet energy profile is essentially flat. In fact, the ⁵TS_H species in the case of PhEt is lower in energy than the reactants onset on the quintet surface. Therefore, on this surface of PhEt the amplitude of the C-H vibration explores the entire region from the reactants to the transition state and beyond to the intermediate ⁵I. Consequently, during the crossover of the reaction complex from the triplet to the quintet surface, the C-H vibration amplitude on the quintet surface will propagate the complex directly to the intermediate ⁵I, and through the triplet barrier resulting in a tunnelling behavior. On the other hand, the deuterated PhEt will have a quintet energy profile with a barrier, so the C-D vibration will not suffice in this case to propagate the reaction complex directly to the intermediate. Thus, whenever the quintet energy profile is very flat, a very large KIE value would be expected.

The observation of large KIE(Q) for TauD, along with the calculations of de Visser[17] which reveal a very flat quintet surface for the H-abstraction reaction of the quintet state, provides further support for this hypothesis.[22]

In contrast to the flat quintet surface in the case of PhEt, the quintet profile for the reaction with MeCN is rather steep, having a net barrier of 10 kcal/mol in the gas phase. This barrier is well above the energy stored in the C-H vibration, and therefore the T-Q crossover and the reaction on the Q surface will proceed in a normal barrier climbing fashion, thus leading to a normal (semiclassical) KIE value.

Our working hypothesis does not depend on the probability of spin crossover, but rather on the shape of the quintet energy curve. While we cannot make definitive specific predictions for other substrates, we can outline trends. Thus, if the barrier on the quintet surface is larger than the zero point energy stored in the C-H bond undergoing activation, the reaction on the quintet surface, after T–to-Q crossover, will behave as a regular barrier climbing reaction, leading to a normal KIE in the semiclassical regime, whereas a quintet surface flatter than or equal to the zero point energy stored in the C-H bond will give rise to a tunnelling-like behaviour, since the C-H vibration will explore a wide range of the quintet potential surface and will propagate the system to the product. Since the H-abstraction barriers are generally proportional to the C-H bond dissociation energies (D(C-H)), with a proportionality constant of 0.3 or so,[21] this suggests that the tunnelling behaviour should be observed in a narrow range of D(C-H) values, with a rather abrupt fall down as the D(C-H) further increases. This seems to be the general appearance in Figure 2.

Another factor is the solvent reorganization. As can be seen from Figure 3, solvation raises the barriers by 4–7 kcal/mol. This means that the tunnelling behaviour should occur prior to solvent reorganization. In turn, the solvent reorganization might exhibit additional KIE due to narrowing of the barrier,[20a] or to a friction-like mechanism that will depend on the nature of the solvent.[23]

In conclusion, the mononuclear, nonheme oxoiron(IV) complexes 1 and 2 are capable of oxidizing hydrocarbon substrates over a wide range of D(C-H) values. The rate dependence of these reactions on D(C-H) suggests a mechanism of H-atom abstraction. This mechanistic proposal is supported by the deuterium kinetic isotope effect that is observed for each substrate studied, including the reaction with solvent acetonitrile. For some of the substrates examined, specifically those with a D(C-H) less than ∼93 kcal/mol, large, non-classical values of k_H/k_D are observed. Such large KIEs suggest a mechanism of hydrogen tunnelling, which other data also support. This behavior is interpreted using the TSR concept: the C-H vibration amplitude propagates the molecular complex from the reactant-like geometry directly to the product whenever the quintet energy surface is flatter than the zero point energy stored in the C-H bond (Figure 3a) undergoing activation. Thus, the TSR concept provides a rationale and a working hypothesis for a substrate-dependent tunnelling mechanism that varies nonintuitively with the C-H bond dissociation energy.