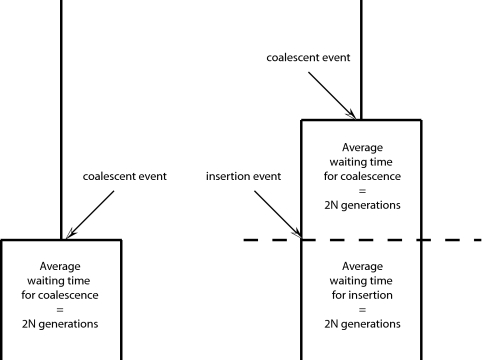
Fig. 1.

Genealogies conditioned on the presence of a rare polymorphic insertion. In a genealogy of two gene copies from a randomly mating haploid population with a constant size of 2N individuals, a coalescent event occurs with probability 1/2N per generation, and an insertion event with probability 2μ, where μ is the insertion rate at the locus. The probability of an event of either type is 1/2N + 2μ, which is ≈1/2N if μ is small. The mean waiting time until the first event (of either type) is thus ≈ 2N. We are considering only those genealogies in which this first event is an insertion. Consequently, there is a second subinterval to consider. By an identical argument, its expected length is also ≈2N. Therefore, the total length of a genealogy conditioned on the presence of a rare mutation is ≈4N, twice the unconditional expectation of 2N. So in the simple case of two samples in a population of constant size, the presence of a rare polymorphic insertion doubles the expected length of the genealogy.