Multi-Subject Analyses with Dynamic Causal Modeling

Abstract

Currently, most studies that employ dynamic causal modeling (DCM) use random-effects (RFX) analysis to make group inferences, applying a second-level frequentist test to subjects’ parameter estimates. In some instances, however, fixed-effects (FFX) analysis can be more appropriate. Such analyses can be implemented by combining the subjects’ posterior densities according to Bayes’ theorem either on a multivariate (Bayesian parameter averaging or BPA) or univariate basis (posterior variance weighted averaging or PVWA), or by applying DCM to time-series averaged across subjects beforehand (temporal averaging or TA). While all these FFX approaches have the advantage of allowing for Bayesian inferences on parameters a systematic comparison of their statistical properties has been lacking so far.

Based on simulated data generated from a two-region network we examined the effects of signal-to-noise ratio (SNR) and population heterogeneity on group-level parameter estimates. Data sets were simulated assuming either a homogeneous large population (N=60) with constant connectivities across subjects or a heterogeneous population with varying parameters. TA showed advantages at lower SNR but is limited in its applicability. Because BPA and PVWA take into account posterior (co)variance structure, they can yield non-intuitive results when only considering posterior means. This problem is relevant for high SNR data, pronounced parameter interdependencies and when FFX assumptions are violated (i.e. inhomogeneous groups). It diminishes with decreasing SNR and is absent for models with independent parameters or when FFX assumptions are appropriate. Group results obtained with these FFX approaches should therefore be interpreted carefully by considering estimates of dependencies among model parameters.

Introduction

Standard analysis in functional magnetic resonance imaging (fMRI) aims at mapping brain regions specifically involved in a cognitive context or in processing a given stimulus. There is, however, growing interest in understanding how these patterns of activation arise by analyzing regional interactions aka connectivity analysis (Stevens, 2009). In addition to extending our knowledge about how information is processed in the brain, understanding the interactions between regions may also be of clinical relevance as converging evidence suggests that dysconnectivity may be a major cause for symptoms encountered in patients suffering from neurological and psychiatric disorders such as primary progressive aphasia (Sonty et al., 2007), schizophrenia (Stephan et al., 2006) or depression (Mayberg, 2003). It is, therefore, vital to employ and further develop techniques that enable non-invasive in vivo assessment of interregional connection strengths.

Several methods are currently used to reveal details of information processing in a neural network. These methods are in general divided into two groups: functional connectivity and effective connectivity (Friston, 2002). Functional connectivity describes statistical dependencies between regional time series using different approaches (e.g. (Beckmann et al., 2005; Biswal et al., 1996)). Functional connectivity analyses, however, do not allow for inferences about the direction or causality of a connection as they are based on a purely correlative measure. Determining causality requires an analysis of the effective connectivity which is, most commonly, defined as the influence of one neural system over another (Friston et al., 1995). In contrast to functional connectivity, a specific causal model has to be defined a priori. Identifying the participating brain regions is commonly accomplished based on standard fMRI activation mapping. Connection strengths between these brain regions are then inferred, given measured fMRI data, using statistical models that embody an anatomically motivated structure of the network (Penny et al., 2004b; Ramnani et al., 2004). As a consequence, effective connectivity methods are strongly hypothesis-driven and require considerable a priori knowledge.

A number of methods to analyze effective connectivity in fMRI have been proposed, including Structural Equation Modeling (SEM; (McIntosh and Gonzalez-Lima, 1991; McIntosh and Gonzalez-Lima, 1994)), Granger causality (GC; (Goebel et al., 2003; Granger, 1969, 1980)) and, most recently, dynamic causal modeling (DCM; (Friston et al., 2003)). Here, we focused on DCM, a method successfully applied to neuroimaging and electrophysiological data, as diverse as fMRI (Friston et al., 2003; Stephan et al., 2008), EEG and MEG (David et al., 2006) and local field potentials from invasive recordings (Moran et al., 2009). Critically, DCM uses a hierarchical approach that includes a model of the (hidden) neuronal processes of interest and a forward model that translates neuronal activity into predicted measurements. In DCM for fMRI, neuronal population activity is linked to region-specific BOLD activity using a biophysical model of the haemodynamic response (Friston et al., 2000; Stephan et al., 2007) based on the Balloon model (Buxton and Frank, 1997; Buxton et al., 1998).

Model estimation within DCM employs Bayesian inversion resulting in a multivariate posterior probability distribution of the estimated model parameters, given measured fMRI data and a specific a priori model (including priors on the parameters). Posterior density analysis then allows for straightforward inferences about model parameters at the single subject level (e.g. (Mechelli et al., 2003; Stephan et al., 2005)).

For group-level analysis of model parameters, however, several approaches are available. The most common method is to enter the subject-specific parameter estimates of interest into a second-level random-effects (RFX) analysis. This method corresponds to a linear model of subject-specific posterior mean estimates aka maximum a posteriori (MAP) estimates and assumes homogenous intra-subject variance across the population. Because it is simple and robust, RFX analysis has found widespread application (e.g. (Fairhall and Ishai, 2007; Grefkes et al., 2008 ; Leff et al., 2008; Noppeney et al., 2006; Siman-Tov et al., 2007; Smith et al., 2006)). There exist other hierarchical models for group analyses that combine intra- and inter-subject variance (Mumford and Nichols, 2006) either in a frequentist (Beckmann et al., 2003; Friston et al., 2005) or in a Bayesian framework (Woolrich et al., 2004). However, these methods have, to our knowledge, not yet been applied in the context of DCM and we have therefore not included them in the present study.

In addition to this RFX analysis, a number of fixed-effects (FFX) methods exist. A straightforward approach applicable in the special case of identical stimulus timings across subjects, is based on DCM of the BOLD time series averaged across subjects (Kasess et al., 2008). This is effectively an analysis of an “average” subject and allows for posterior density assessment as performed in single–subject analysis. Alternatively, (Garrido et al., 2007) suggested the use of a fully Bayesian FFX approach where the subject-specific posterior distributions are combined according to Bayes’ theorem (Neumann and Lohmann, 2003). Such a Bayesian approach has several interesting features. In contrast to null hypothesis testing based on maximum likelihood parameter estimates in frequentist analyses, the Bayesian approach delivers the parameter’s full posterior density, thus allowing one to directly assess the conditional probability that the parameter exceeds a certain threshold or lies in a particular range. Another advantage of the Bayesian approach is that the precisions of the multivariate subject-specific parameter estimates are also taken into account. A third possible FFX approach would be to perform univariate Bayesian FFX group analysis, disregarding posterior between-parameter correlations (Neumann and Lohmann, 2003).

It is important to note that in this simulation study all methods (RFX and FFX) are applied to the parameter distributions of a given model whose parameters may vary across the group (for the inhomogenous population studied below) but whose overall structure remains constant. In contrast, in analyses of empirical group data, an optimal model for the group has to be selected first before inferences about any parameters can be made. There exist both, FFX and RFX, approaches for model selection at the group level (Stephan et al., 2009) which evaluate the evidence of the competing models (Penny et al., 2004a). These methods, however, are not subject of this particular study which focuses on inference about parameters, not model structure, and assumes that an optimal model is already known or selected.

Whereas the large majority of previous DCM studies have used RFX group analyses of model parameters, these are not always preferable to an FFX approach. The choice between FFX and RFX analyses depends on the assumptions about variability that are most appropriate for the scientific question of interest (Wilk and Kempthorne, 1955). Whenever the mechanism of interest, encoded by a specific model parameter, is likely to be a random variable in itself, and the error variance thus reflects both observation noise and variation of the mechanism across subjects, an RFX procedure is mandatory. This is the case, for example, when examining higher cognitive functions that can be implemented in different ways (Price and Friston, 2002) or when studying patient groups that are heterogeneous with regard to the pathophysiological processes involved (Stephan et al., 2006). In contrast, when the mechanism (parameter) of interest can be assumed to exist as a fixed variable in the population (e.g. processing of low-level visual features in V1), it is perfectly appropriate, and indeed statistically more efficient, to employ an FFX procedure and treat all of the variability in the data as observation noise.

When an FFX analysis is appropriate to address the question of interest, it has two major advantages compared to an RFX analysis. First, it is statistically more efficient because it operates on a much larger dataset (all measured data points across subjects, as opposed to the set of subject-specific parameters). Secondly, it provides a single posterior density for the entire group and thus enables one to make Bayesian inferences about the parameter itself, given the data; in contrast, this is impossible with classic non-Bayesian RFX approaches. What is less clear, however, is whether the different implementations of FFX methods described above have particular advantages or disadvantages in practice. To date, no systematic evaluation of their statistical properties has been performed. Given the growing number of DCM studies that report group results and the increasing use of Bayesian group analyses in DCM (for EEG, see (Garrido et al., 2007); for fMRI, see (Stevens et al., 2007) and (Acs and Greenlee, 2008)), it would be important to assess the impact of the above FFX methods on group inferences.

Therefore, the aim of this study was to yield quantitative results on group analysis performance comparing the following three FFX methods: (1) full Bayesian averaging based on the multivariate posterior parameter distribution (referred to as Bayesian parameter averaging, “BPA”), (2) a Bayesian analysis where posterior covariances are ignored and the posterior probability distributions are effectively treated in a univariate fashion (posterior variance-weighted averaging, “PVWA”), and (3) initial averaging of the time series across subjects (temporal averaging, “TA”). For comparison, a classic RFX analysis (“RFX”) was performed. Our comparisons were based on simulated data with known parameter values across a wide range of signal-to-noise ratios (SNR). In addition, the effects of inter-subject variability were investigated in the context of large sample populations (N = 60) and smaller subsamples (N = 15) as commonly encountered in current fMRI studies.

Materials and Methods

Dynamic Causal Modeling

In short, DCM for fMRI models the activity in a set of interconnected neuronal populations using a set of coupled bilinear first order differential equations where z is a vector of regional neural population activities:

$$\stackrel{.}{z}=Az+\sum _i{u}_i{B}^{\left(i\right)}z+Cu$$ (1)

This system of equations allows for activity within a region to be driven not only by the activity of other regions (matrix A) but also directly by external inputs u (matrix C). Furthermore, DCM allows for context-dependent changes in interactions between regions (matrices B⁽ⁱ⁾). Note that equation 1 exclusively describes neuronal processes; the resulting BOLD signal is separately modeled for each region using a system of nonlinear differential equations characterized by six hemodynamic parameters per region (Stephan et al., 2007).

The neuronal and hemodynamic parameters are jointly estimated using a Bayesian inversion scheme, given the measured BOLD data y and the prior densities of the model parameters, which define the general structure of the network. This inversion results in a multivariate posterior parameter distribution which not only allows for inference about individual parameters, but also for assessment of statistical dependencies (i.e. posterior correlations) between different parameters (c.f. (Stephan et al., 2007)). These parameter distributions are assumed to be multivariate Gaussian, i.e. they are fully characterized by the parameters’ means and covariances. This has previously been shown to be an appropriate assumption for fMRI data (Chumbley et al., 2007).

Group analysis methods

Currently, several methods for group-level analysis of single-subject dynamic causal models exist. Most commonly used is a classical RFX analysis that is based on the sole use of the posterior mean estimates or maximum a posteriori estimates (MAPs; (Friston et al., 2003)). This classic analysis uses the same “summary statistics” approach as is commonly used for group analyses in statistical parametric mapping (Penny and Holmes, 2004): subject-specific parameter estimates of interest are entered into a second-level frequentist test, e.g. a t-test. The only difference is that for DCM the parameter estimates are maximum a posteriori (MAP) estimates, not maximum likelihood estimates as in SPM. Notably, this approach does not account for dependencies among parameters and assumes that the variance of the single subject parameter estimates is homogenous across the population. This method will be denoted as “RFX” analysis throughout the paper.

Concerning FFX methods, there is a well-known fully Bayesian procedure that does account for these two subject-specific properties when forming a joint posterior for the entire group (Lee, 1989). This fixed-effects procedure has been applied previously for fMRI activation maps based on the general linear model (Neumann and Lohmann, 2003). Effectively, this procedure treats the posterior distribution of one subject as the prior for the next subject. The resulting posterior, in turn, acts as the prior for the next subject and so on, resulting in the following expression for the group joint posterior

$$\begin{array}{cc}\hfill p\left(\theta \mid y_1,\dots ..,y_N\right)\propto & p\left(\theta \right)\prod _{i=1}^{N}p\left(y_i\mid \theta \right)\hfill \\ \hfill \propto & p\left(\theta \mid y_1\right)\prod _{i=2}^{N}p\left(y_i\mid \theta \right)\hfill \\ \hfill \propto & p\left(\theta \mid y_1,y_2\right)\prod _{i=3}^{N}p\left(y_i\mid \theta \right)\hfill \end{array}$$ (2)

Note that this procedure is commutative, i.e., it does not depend on the order of subjects. Under Gaussian assumptions about the densities (as in DCM) this procedure is significantly simplified, and the above expression is reduced to a form where subject-specific conditional parameter densities are weighted by their precision and summed across subjects (c.f. (Garrido et al., 2007; Neumann and Lohmann, 2003)):

$$\begin{array}{cc}\hfill \mu =& {\Lambda }^{-1}\sum _{i=1}^N{\Lambda }_i{\mu }_i\hfill \\ \hfill \Lambda =& \sum _{i=1}^N{\Lambda }_i\hfill \end{array}$$ (3)

with μ_i being the posterior mean of the i^th subject and ${\Lambda }_i={\sum }_i^{-1}$ the inverse posterior covariance or precision matrix. Note that Λ not only represents the precisions of model parameters (on its diagonal) but also how strongly parameters are interdependent (off-diagonal elements of Λ).

Under Gaussian assumptions about priors and likelihoods, the joint posterior probability p(θ | y₁…y_N) in Eq. 2 is also Gaussian with a posterior mean μ and a posterior covariance matrix Λ⁻¹ . Note that this type of Bayesian averaging is not to be confused with Bayesian model averaging (e.g. (Trujillo-Barreto et al., 2004)) where the posterior distributions of different models are combined by weighting with the respective model evidence. The method used here is applied to one model only, fitted to the data from several subjects (typically, this model would be chosen using a Bayesian model-selection procedure; c.f. (Penny et al., 2004a) or (Stephan et al., 2009)). In order to prevent confusion, we will refer to the present method as “Bayesian parameter averaging”, or BPA, throughout the paper. The RFX analysis described above and BPA can be viewed as representing extremes of spectrum of the averaging methods where intra-subject variances and covariances are either completely ignored (RFX) or fully incorporated (BPA).

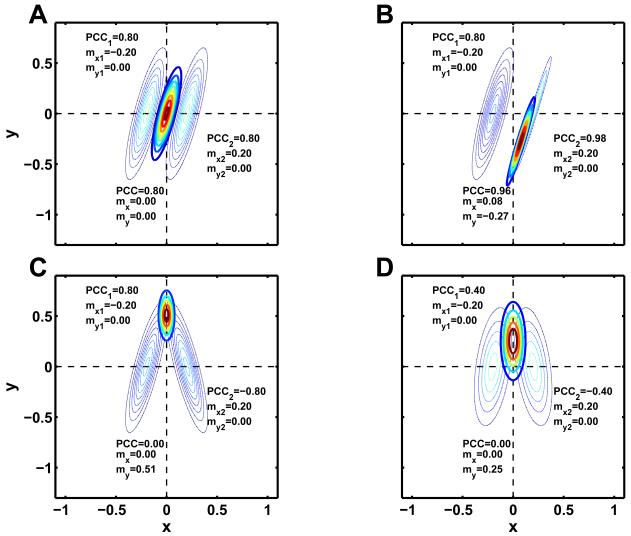
At this point it may be instructive to illustrate this issue by examining the products of Gaussians as they appear in BPA and show how different parameter distributions can affect the outcome. As can be seen from Eq. 3 both the diagonal (variance) and off-diagonal values (covariances) of the covariance matrices influence the mean of the resulting Gaussian. Fig. 1 shows four examples of these effects, using two bivariate Gaussian probability distributions, where each distribution is characterized by its mean [m_x, m_y] and covariance matrix; for simpler interpretation, the covariance (off-diagonal element) is normalized to give a posterior correlation coefficient (PCC), ranging from −1 to 1. In the case of multiplying two bivariate Gaussian distributions with different means but identical covariance (fig. 1A), the resulting mean [m_x, m_y] is equal to the arithmetic average [m_x1+m_x2, m_y1+m_y2]/2. As can be deduced from Eq. 3, the PCC of the resulting distribution is unchanged while the variance in x- and y-direction is reduced. If, however, both distributions exhibit different dependencies or covariances (fig. 1B, C and D), then the resulting distribution will be shifted away from the arithmetic mean. In fig. 1B it can be seen that, in the case of differing precisions the resulting distribution will be shifted towards the Gaussian with the higher precision. Additionally, depending on the covariances of the two Gaussians, the range of their means may no longer contain the posterior mean resulting from Eq. 3. For example in fig. 1B, the posterior mean m_y is −0.27, even though both m_y1 and m_y2 are zero. A perhaps even more counterintuitive effect is shown in fig. 1C and 1D where covariances of identical value but opposite sign cause a pronounced deviation of the posterior mean from m_y1 and m_y2, despite identical precisions.

Fig. 1.

Product of two Gaussians: Shown are contour plots of two bivariate Gaussian distributions (thin lines) and the resulting product (bold lines). In all four plots both distributions have zero mean in y and +/−0.2 in x-direction and a variance of 0.1 in y and 0.01 in x. In (A), (B) and (C) the left Gaussian is kept constant with a PCC=0.8 whereas the right Gaussian has a PCC of 0.8, 0.98 and −0.8 respectively. (D) shows the same data as (C) with a lower PCC of +/−0.4. The resulting PCC and the mean in x and y direction are also shown. Dashed lines mark the arithmetic mean as recovered in RFX analysis.

A second FFX method for group-level inference about DCM parameters is to perform univariate Bayesian parameter averaging (Neumann and Lohmann, 2003) where each MAP estimate is weighted by its posterior variance while covariances between parameters are ignored; in other words, only the diagonal elements of the posterior covariance matrices are used in this approach. In order to not confuse it with the multivariate case (i.e. BPA), this method will be referred to as “posterior variance-weighted averaging” or PVWA.

A third FFX option is to average BOLD time-series across subjects before applying DCM, resulting in a single model that represents an “average” subject (Kasess et al., 2008; Li et al., 2008). As for the other two FFX methods, this approach allows one to make group inferences based on a single posterior density for the entire group. Although this method is the simplest and the computationally most efficient, it is only applicable when stimulus timing is identical across subjects. This method will be referred to as “temporal averaging” or TA throughout this paper.

Simulated network

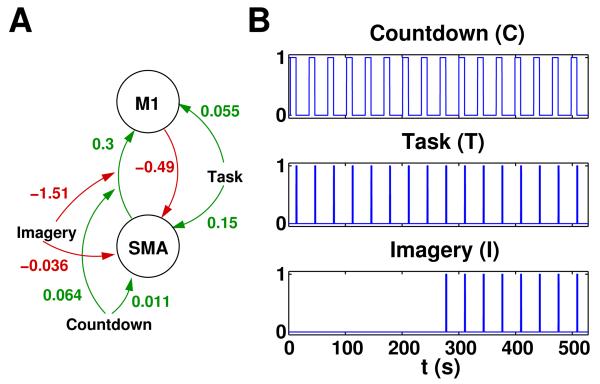
Our aim was to evaluate the different DCM averaging methods in terms of estimation accuracy when applied to known parameters with pronounced interdependencies or covariances as they are frequently encountered in biological systems (Gutenkunst et al., 2007). Additionally, we examined the influence of varying observation noise and population heterogeneity. For this purpose, we generated simulated data using a two-region DCM consisting of the supplementary motor area (SMA) and the primary motor cortex (M1) (Kasess et al., 2008). The original measurements were performed on a 3 Tesla Medspec scanner (Bruker Biospin, Germany) using gradient-recalled EPI with a TE of 40ms and a TR of 300ms (Kasess et al., 2008). The paradigm consisted of brief finger movements that subjects either executed (motor execution) or imagined (motor imagery); finger movements were preceded by an acoustic countdown lasting 10 seconds. 28 different models were tested and compared by Bayesian model selection; the best-performing model formed the basis for the simulations within the current study (fig. 2). Note that this model is particularly well suited for the present methodological study since the recurrent use of the same inputs induced considerable parameter interdependencies (the posterior correlations ranged from −0.82 to 0.81).

Fig. 2.

Simulated network: (A) Motor network as found in (Kasess et al., 2008). Note that modulatory parameters are half of the value published by (Kasess et al., 2008) due to a change in scaling across SPM versions. (B) During the 10 second countdown “C” subjects prepared for execution or imagination “I” of a brief finger tapping task “T”.

Simulations

In this simulation study the population size was initially chosen to be 60 subjects. Since this is high compared to typical fMRI sample sizes, we subsequently performed our analyses using a subsampling approach in which subsamples of 15 subjects were drawn repeatedly out of the population of 60 (see below). TR and TE were identical to the original data sets. The model equations (i.e. the neuronal equation described by Equation 1 and the hemodynamic equations described in (Stephan et al., 2007) were integrated at a temporal resolution of 100 ms.

The primary aim of this study was to evaluate the performance of the different FFX group analysis approaches under different levels of noise when the underlying assumptions were valid, i.e. model parameters were indeed fixed effects in the population and thus all variability was due to observation noise. We therefore generated data sets with eight different levels of additive Gaussian observation noise, resulting in a range from very low to very high signal-to-noise-ratios (SNRs): 0.05, 0.2, 0.5, 1, 2, 5, 10 and 50. SNR was defined as the ratio of the standard deviations of the noise free signal and the noise process. The noise was included in our data by adding it to the noise-free simulations. Note that the range of SNRs used for these simulations is rather wide and includes values that are both unrealistically low and high for fMRI. We chose this wide range of values to demonstrate more clearly the behavior of the different methods and explore their behavior for extreme SNR constellations as well.

A second aim was to investigate the performance of FFX methods when their underlying assumption is violated, i.e. when the parameter of interest is not a fixed effect in the population but a random variable. Therefore, we used a generative model in which connection strengths were treated as random effects, and thus varied stochastically across subjects, by adding zero-mean Gaussian noise processes to the parameter values shown in fig 2 such that each parameter was varied independently from the others. This variation left the mean population parameters unchanged and parameters uncorrelated across the population. For endogenous connections (i.e. non-zero off-diagonal elements of the A matrix in Equation 1) the variance of the Gaussian noise was chosen such that there was approximately a 5% chance for each connection strength of changing sign. Stimulus-related connections, i.e. modulatory inputs (B matrices) and driving inputs (C matrix), were less strongly varied (half the standard deviation) in order to avoid inverse stimulus effects. The temporal scaling parameter (i.e. the value of the diagonal of the A matrix) and haemodynamic parameters were kept constant.

In summary, analyses were performed using (i) eight different levels of Gaussian observation noise and (ii) parameters that were either constant or varied randomly across the synthetic “subjects” yielding a homogeneous and a heterogeneous population, respectively. This resulted in a total of 16 different sets of data, each comprising 60 single-subject data sets. All data sets were generated using the simulation routine “spm_dcm_create” as provided by SPM5 and no confounding effects where added.

Estimation

Model inversion was performed using the Bayesian inversion scheme of the DCM software as implemented in SPM5. The same model structure was defined as used for generating simulated data sets and all prior densities were set to their default values

Comparison

Results of the different averaging procedures were compared by calculating the total absolute deviation, i.e. the L1 norm, of the group-averaged parameter estimates from the true population mean:

$$D=\sum _{j=1}^p\mid {\widehat{\mu }}_j-{\mu }_j\mid$$ (4)

where μ_j is the true population mean of the j-th parameter and ${\widehat{\mu }}_j$ is its estimate as calculated by one of the four averaging methods (RFX, BPA, PVWA, and TA).

In order to further assess the resulting group parameter distributions, we also examined the posterior correlation matrices of estimates obtained by BPA and TA, respectively. These posterior group correlation matrices were compared to two different quantities: (i) the median of the posterior single-subject correlations across subjects and (ii) the correlations among subject-specific MAPs across the population. With this approach it is possible to assess how group correlations are related to single-subject posterior correlations and how single-subject MAPs are affected by posterior single-subject correlations. Note that this analysis is not meaningful for the PVWA approach, where posterior covariances are ignored.

Subsample analysis

It seems clear that a group size of 60 subjects is unrealistically high for a typical fMRI study. All averaging methods were therefore also evaluated for subsamples of 15 subjects. 100 samples were generated by randomized selection of 15 out of the 60 subject data sets (without replacement), and the connectivity parameter averages were calculated for each subsample using the different averaging methods as described above. In the case of temporal averaging the BOLD series were averaged for each subsample and a model was estimated for each of the 100 composite time series. Connection strengths were compared to the true parameter values of the corresponding subsample based on D (Equation 4) and the median as well as the inter-quartile range of deviations across subsamples were calculated. Furthermore, PCCs derived from BPA and TA, as well as the correlation of the MAPs and the median single-subject posterior correlations were calculated for each subsample. Then the medians across subsamples of all four correlation coefficient matrices were compared.

Results

Population results

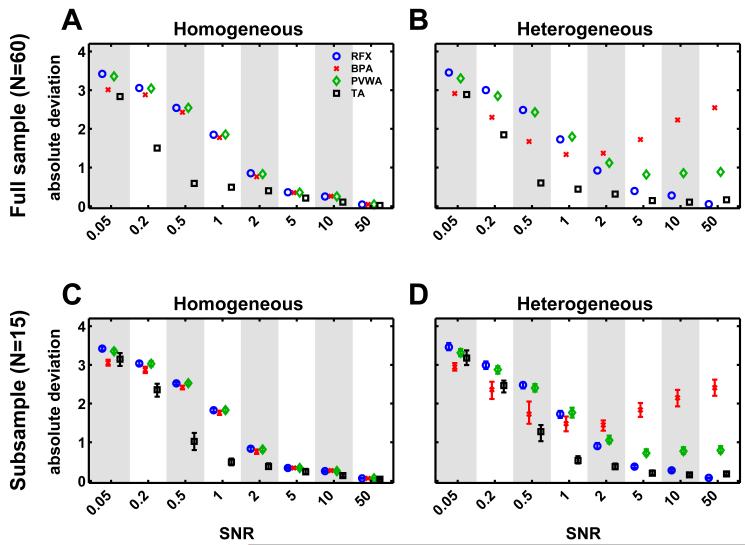
Results for data sets from the simulated homogenous population where the assumptions of FFX analyses were met (i.e. parameters were identical across the group and all variability was due to observation noise) showed a similar average deviation for RFX, BPA and PVWA approaches (fig. 3A). Temporal averaging yielded considerably less deviation from the true parameter values at low SNR-levels due to the fact that the SNR-level increases by the square root of the number of subjects when averaging the data across multiple subjects. In our study this was a factor of approximately eight which was in good agreement with the shift in SNR levels. Overall deviations decreased with higher SNR as expected and leveled off at SNRs greater than 5, above which all averaging approaches showed almost identical performance.

Fig. 3.

Comparison of group analysis methods: The upper two panels show the deviation of the different averaging methods with respect to the original parameters as a function of the SNR of the simulated data. (A) shows results for the homogeneous population and (B) shows results for the heterogeneous population. (C) and (D) show the range of deviations for 100 subsamples of size N=15 for the homogeneous and the heterogeneous case, respectively. Error bars are plotted to show the median and the inter-quartile range across the subsamples. Alternating grey and white patches are shown in order to better distinguish the different SNRs.

The analysis for the simulated inhomogeneous population where the FFX assumptions were violated (i.e. model parameters varied randomly across subjects) showed considerably less convergent results (fig. 3B). As expected, results for the classic RFX analysis (whose assumptions about parameters being random effects were appropriate for this data set) were similar to the homogeneous dataset. Temporal averaging results were also similar to the homogenous case. At low SNRs, BPA showed better results than RFX and PVWA. With SNR levels above 1, however, BPA results began to deviate more strongly from the true parameter values, while RFX and TA results moved closer to the true values. PVWA showed intermediate performance with a less drastic deviation at high SNRs than Bayesian parameter averaging. Figure 3C and D show the same results for a smaller sample size (see subsample section below).

The seemingly counterintuitive behavior of BPA with increasing SNR is directly related to the fact that BPA takes into account the posterior covariance structure: a progressive increase in noise (i.e. decreasing SNR) will tend to render any posterior parameter distribution less correlated. In other words, low SNR mitigates the effects of parameter interdependencies or posterior covariances, whereas at high SNR these covariances can have a profound impact on products of Gaussians. Compare fig. 1, where panels C and D represent the case of shifting from a high SNR case to a low SNR case.

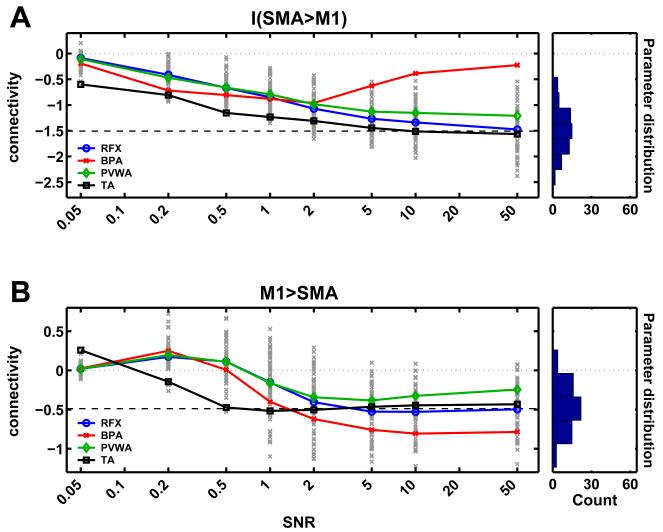
In the following we will investigate the behavior of the different averaging methods in more detail, focusing on the case of the heterogeneous population. Fig. 4 shows the detailed results for two parameters, namely the modulation of the connection from SMA to M1 by motor imagery (fig. 4A), and the endogenous connection strength from M1 to SMA (fig. 4B). The true mean parameter values are indicated by the dashed horizontal line and single-subject estimations are shown be grey “x”-marks. It can be seen that for low SNRs, single-subject intrinsic and modulatory connection strengths are underestimated yielding group averages closer to zero for all approaches. This is the expected effect of the zero-mean shrinkage priors in DCM defined for these types of connection. Direct stimulus inputs (not shown here) do not show such a clear trend as they have less precise priors and thus exert less shrinkage. Fig. 4A shows that while the estimation accuracy improves with increasing SNR for TA, PVWA and RFX, for SNRs greater than 2 the group-estimate of connection strength provided by BPA increasingly underestimates the mean of the parameter distribution even though the single-subject estimates were quite accurate. Moreover, for SNRs greater than 5, the average of the modulatory connection lies outside the actual range of the individual parameter estimates. In the case of the endogenous connection (fig. 4B), however, the deviation is less pronounced and shows an opposite trend towards overestimation (in absolute terms) of connection strengths. It is important to note, however, that the type of connection is not a general indicator for the direction of bias in BPA. In contrast, PVWA in both cases tends to underestimate connection strength at high SNRs.

Fig. 4.

Single parameter comparison: (A) Estimation of a single parameter (modulatory influence of motor imagery on the connection SMA → M1) as a function of the SNR. Coloured solid lines represent different averaging methods (colour scheme as in fig. 3). Single-subject MAPs for a given SNR are marked by “x”. The box on the right side shows the true model parameters distribution. The dashed black line marks the mean of the model parameter. (B) Analogous results for the feedback connection from M1 to SMA.

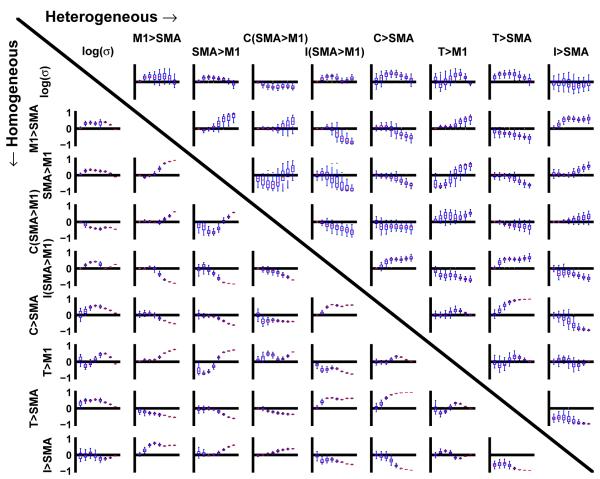
Fig. 5 shows the distribution of single-subject PCCs for all nine model parameters (including the temporal scaling factor σ) in case of the homogeneous (lower left triangle) and the heterogeneous population (upper right triangle). Each subplot contains the results for all eight SNR levels (increasing from left to right) displayed as box-and-whisker plots. For reasons of clarity, outliers are not shown. It can be seen that in the homogeneous case PCCs (lower left triangle) exhibited much less variation across subjects compared to the heterogeneous population (upper left triangle). In the latter case, not all parameter combinations displayed a monotonic decrease of PCC variability with increasing SNR. Instead, for a few parameter combinations, PCC variability was enhanced with increased SNR or showed non-monotonic behavior for others.

Fig. 5.

Correlation coefficients: Plots show the posterior single-subject correlation coefficients of model parameters for the homogeneous (lower left half) and the heterogeneous (upper right half) population. Each box-plot shows distribution of PCCs for 8 different SNRs (see fig. 3). SNR increases from left to right. Blue boxes show median and inter-quartile range. Outliers are not shown for reasons of clarity. Each column and row corresponds to one parameter.

Note that although PCCs from the heterogeneous population exhibited much stronger scattering as compared to PCCs from the homogeneous population, correlation medians were similar for both types of data sets (see also left column of fig. 6). As expected, most PCC medians showed an increase in parameter interdependencies with increasing SNR (c.f. fig. 1C and 1D). Additionally, the inter-subject variability in parameter values leads to posterior distributions with more heterogeneous correlation structures. Together, these properties explain the seemingly counterintuitive BPA results for the group average in fig. 3.

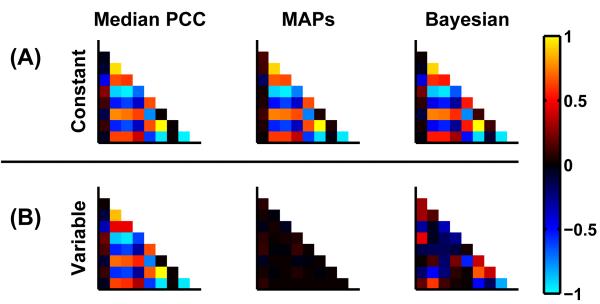
Fig. 6.

Group correlations calculated by different methods (left to right): (i) median posterior correlations across subjects, (ii) correlation of MAPs and (iii) BPA. The upper row (A) depicts the case of the homogeneous population whereas the lower row (B) represents the heterogeneous population. The results for SNR=50 are shown. Rows and columns of each matrix are in the same order as in fig. 5.

BPA as well as TA yield a single multivariate Gaussian parameter distribution for the whole group that is characterized by the group posterior mean (e.g. fig. 4A and B) and the group posterior correlation matrix. For the homogeneous population, the median correlation across subjects (fig. 6A, left panel) exhibited strong single-subject correlations. As these correlations were consistent across subjects (fig 5, lower triangle) BPA showed a very similar group correlation matrix (fig. 6A, right panel). Fig, 6A, centre panel, shows that, for a perfectly homogenous population, correlations of the MAPs across subjects are induced by single-subject correlations. The median correlation matrix of the heterogeneous population (fig. 6B, left panel) was similar to that of the the homogeneous population (fig. 6A left panel and also fig. 5). As parameters were randomly varied and thus uncorrelated across subjects, MAPs (fig 6B, middle panel) showed no significant correlation across the population. BPA (fig. 6B, right panel) displayed less strong correlations, but similarities with the median PCC matrix were still observable. In case of TA, correlations were very similar to the median correlation matrix for both populations.

Subsample analysis

The subsampling analysis (fig. 3C and D) yielded results that were very similar to the analysis of the whole population (fig. 3A and B). Again, for homogeneous subpopulations all methods showed decreasing error for higher SNRs, and variation across subsamples were small. Note that the shift to lower SNRs for TA was smaller due to the reduced sample size (N=15). In case of the heterogeneous subpopulations, however, BPA again showed increasing deviations at high SNRs and a better performance at low SNR, as was the case for the whole population. As expected, these deviations varied considerably across subsamples (see the range of deviations represented by the error bars in fig. 3C, D). Median correlations across subsamples were similar to the full population analysis shown in fig. 6.

Discussion

In this study, we analyzed four common methods for making group inferences about DCM parameter estimates. Of particular interest were the results of different FFX methods that enable Bayesian inference by analysis of a group posterior density as compared to a classic RFX analysis which allows only for testing the null hypothesis i.e. obtaining the data given that the respective parameter (or contrast of parameters) does not differ from the hypothesized value which is, most commonly, zero. The properties of the different methods were investigated using simulated data sets with known model parameters. Although the emphasis of the present investigation was on comparing different FFX procedures, it is worth noting that the classic RFX procedure employed by most current DCM group studies showed robust performance, both for homogenous and heterogeneous groups. As mentioned, this RFX procedure assumes constant intra-subject variability of the parameter estimates across the population as only the MAPs are taken into account. There exist, however various models that do combine inter- and intrasubject variance to infer group statistics (Mumford and Nichols, 2006). In the classical setting (Beckmann et al., 2003) calculating the group statistics comes down to a sum of the parameter estimates weighted by the sum of the inter- and intrasubject variance. From this it is clear that the group estimate should lie between our RFX approach and the PVWA method. The Bayesian RFX approach (Woolrich et al., 2004) is based on prior assumption about the group statistics. As pointed out previously, a hierarchical Bayesian RFX approach might be a more informed way of inferring group statistics (Garrido et al., 2007). However, such a method has not yet been implemented for DCM.

Our study demonstrated that DCM group results were consistent across methods when dealing with a homogeneous group, i.e. when the assumptions of FFX analyses were valid. TA performed best (in terms of showing the smallest deviations between parameter estimates and true parameter values); this is caused by the implicit SNR-enhancing preprocessing step due to data averaging (over subjects) prior to parameter estimation. BPA, classic RFX analysis and PVWA yielded similar parameter estimates.

For a heterogeneous group where parameters varied across subjects (thus violating the FFX assumption that the parameter is a fixed effect in the population and all variability is due to observation noise), BPA results showed a noticeable bias compared to the results of the other methods and the true mean parameter values (figs. 3 and 4). This bias, however, depended on the degree of observation noise and only became obvious for SNRs greater than 2. We were able to relate this effect to two different causes (fig. 5). The first one is an increase in parameter interdependencies with increasing SNR (c.f. fig. 1C and 1D). Additionally, the inter-subject variability in parameter values resulted in posterior distributions with heterogeneous correlation structures.

Since BPA as well as TA produce group densities, we also investigated the resulting group posterior correlation matrices. These posterior correlations imply dependencies amongst the parameters of the model. In simple terms, the posterior variance of a parameter relates to the range in which the parameter can be varied without inducing a large change in the objective function. In other words, large posterior variances imply that the parameter estimate is not very certain given the data and a priori information. Furthermore, if two parameters show a strong posterior covariance then changing either of these parameters has a similar impact on the objective function. The structure of the posterior covariance matrix itself depends on a number of factors, e.g. the predefined model structure, including location and temporal nature of inputs, the structure of the connectivity matrix as well as the strength of the connections. Most importantly for the present study, as described above, an increase in noise (i.e. a decrease in SNR) diminishes interdependencies amongst parameters. This is reflected by our simulation results as BPA performs better than PVWA and RFX analyses for SNR-levels below 1 (fig. 3).

All findings were replicated for smaller sample sizes using population subsampling. In addition, subsampling showed that BPA is highly dependent on the specific sample and may therefore be susceptible to outliers at smaller sample sizes. This is in contrast to (Neumann and Lohmann, 2003) who proposed that this method should be robust against outliers. However, they restricted their analysis to univariate data which in our case also showed much less dependency on the subsample.

To our knowledge, this study provides the first systematic analysis of different group analysis methods for DCM parameter estimates. A study by (Garrido et al., 2007) which focused on the consistency in model selection across subjects, also briefly commented on inter-subject variability for parameter estimates (using MANOVA they found that these estimates were consistent across subjects). They did not, however, provide a systematic comparison of different FFX analysis procedures nor did they consider different noise levels or different population heterogeneities, thus providing no conclusions about the relative pros and cons of different group analysis methods.

As pointed out in the introduction, the choice between RFX and FFX approaches ultimately boils down to one’s assumptions whether the mechanism of interest, encoded by a specific model parameter, exists as a fixed effect in the population or randomly varies across subjects. If an FFX analysis is an appropriate option, it can have several advantages over a classic RFX analysis, including the use of the group posterior density for Bayesian inference. Our analyses show that the three different FFX methods display different performance depending on the level of noise and whether or not the FFX assumption is fulfilled (i.e. the parameter exists as a fixed effect in the population). Although the temporal-averaging approach has advantages at lower SNR, it is limited in its applicability because the timing of stimuli has to be the same across subjects which excludes self-paced paradigms and experiments where stimulus presentation is depending on subject responses or post- experimental classifications of trials (e.g. remembered vs. forgotten items). Furthermore, TA may prove problematic when pronounced non-linearities exist in the system of interest, either in the hemodynamic forward model (Stephan et al., 2007) or at the level of neuronal interactions (Stephan et al., 2008), especially in a heterogeneous population. BPA as well as PVWA do not have these restrictions and account for intra-subject covariance and variance, respectively. However, in high SNR settings and when FFX assumptions are violated (i.e. parameters are not fixed effects in the population), the latter property may cause biased parameter estimates. It is therefore recommended that such results are interpreted with care and in the light of the subject-specific posterior covariances amongst model parameters. Fortunately, the latter are easily obtained as they are automatically estimated as part of the Bayesian model inversion.

In summary, while the primary goal of our study was a comparison of FFX methods in the context of DCM, it is also informative with regard to performance differences between RFX and FFX methods in general because we systematically included simulations that either assumed parameters to be fixed or random across the population (i.e. homogenous or heterogeneous populations). Our simulations showed that RFX analysis performed robustly in all situations (Fig. 3A-D); for low SNRs, however, TA was superior in all scenarios considered (Fig. 3A-D). PVWA performed very similar to RFX when the population was homogenous (Fig. 3A,C); however, with heterogeneous populations, PVWA only showed comparable performance to RFX under low SNR conditions but performed less well than RFX for high SNR data (Fig. 3B,D). A stronger difference was found for BPA: this method displayed considerably poorer performance than RFX (and all other methods) at high SNRs when the population was heterogeneous (Fig. 3B,D) but, on the other hand, worked better than RFX at very low SNR (and similarly well as TA) in the same setting. For homogenous populations BPA was equivalent to RFX at all SNRs (Fig. 3A,C). This summary highlights that despite the bias observed in some situations, BPA is not necessarily an inappropriate method. BPA does not perform worse than other FFX or RFX methods when (i) FFX assumptions are appropriate (i.e. parameters are fixed effects in the population), (ii) parameter interdependencies are absent, or (iii) SNR is low. In fact, for very low SNR and inhomogeneous populations it showed better performance than almost all other methods and was only rivaled by TA (Figure 3A,C). Ultimately, the choice between the different methods studied in this paper should be informed by the investigator’s assumption about the heterogeneity of the population, the assumed SNR level and whether or not she/he wishes to obtain Bayesian inference about the posterior densities of the parameters (which is possible for TA, PVWA and BPA but not for classic RFX). The analyses presented in this paper hopefully assist the reader in making this choice.