Abstract
An ultrasensitive cantilever, oscillating parallel to a surface in vacuum, is used to probe weak thermal electric field gradient fluctuations over thin polymer films. We measure the power spectrum of cantilever frequency fluctuations as a function of cantilever height and voltage over polymers of various compositions and thicknesses. The data are well described by a linear-response theory that calculates stochastic electric fields arising from thermally-driven dielectric fluctuations.
Development of a wide range of electrical, optical, magnetic, and biological sensors and devices requires new approaches to mapping properties of films. A large collection of scanned probe microscopies now exists for generating nanometer-resolution surface maps of chemical forces,1–3 magnetization,4,5 electrostatic potential,6,7 and capacitance.6,8 A scanned probe approach to collecting dielectric spectra has recently been demonstrated.9,10 Developments in the fabrication of attonewton-sensitivity cantilevers11,12 have created new possibilities for ultrasensitive detection and nanometer-resolution imaging of magnetic resonance,13,14 dopant density in semiconductors,15 electric field fluctuations over metals16 and in dielectric films,17–19 and — as we will show here in experiments on polymers — electric field gradient fluctuations.
Non-contact imaging of dissipation, and hence local fluctuations, by scanned probe microscopy was first accomplished by Denk and Pohl, who detected electrical dissipation in GaAs as a sample-induced change in the mechanical quality factor of a charged atomic force microscope cantilever.20 Scanned probe studies of electrical dissipation due to eddy current damping in metals,21 bias-induced free carriers22,23 and dopant-induced free-carriers15 in semiconductors have since been reported, as has imaging of magnetic dissipation due to domain wall motion in ferromagnets.24,25
Stipe et al., in their study of the noncontact friction experienced by an ultrasensitive cantilever over a gold surface in high vacuum16 applied a fluctuation-dissipation relation connecting the noncontact friction coefficient Γ to the fluctuating electric field δEx(t) that couples to the tip charge qc:
| (1) |
with kB Boltzmann’s constant, T the temperature, fc the cantilever frequency, CδEx (t) ≡ 〈δEx(t) δEx(0)〉 the equilibrium correlation function of the fluctuating electric field at the cantilever tip generated by the sample, and δEx the component of the electric field parallel to the interface. These ultrasensitive measurements of noncontact friction have motivated subsequent theoretical26–30 and experimental work17–19,31,32 devoted to understanding the possible sources of electric field fluctuations over a metal sample.
Kuehn et al. used ultrasensitive cantilevers11,12 in a non-contact friction measurement to quantify fluctuating electric fields over polymer samples.17 These measurements were analyzed by calculating Γ from eq 1, with CδEx (t) determined from a dielectric continuum model.18,19 In this picture, the cantilever friction arises from thermal dielectric fluctuations in the polymer film, and Γ is determined by the polymer’s complex-valued relative dielectric function at the cantilever frequency. Using measured values of the dielectric function, and an estimate of the tip-sample capacitance to relate the tip-sample voltage to qc, Kuehn et al. showed that eq 1 agreed well with the measured friction for three polymer species over a range of sample thicknesses and probe heights.
Israeloff and coworkers were the first to access the dielectric spectrum of a polymer by means of scanned-probe microscopy. They observed cantilever frequency fluctuations (jitter) above the surfaces of thin polymer films in vacuum.33–35 They interpreted these cantilever frequency fluctuations as generated by a fluctuating electrostatic potential arising from thermal dynamics in the film. In their analysis, the power spectrum of cantilever frequency fluctuations was related to the absorptive part of the dielectric function of the film,33–35 but the dependence of frequency noise on probe height and film thickness was not explicitly given.
An important difference between the measurements of Israeloff and coworkers33–35 and those presented here is the experimental geometry. In the measurements of Refs. 33–35, the cantilever tip moves perpendicular to the vacuum-polymer interface, as in most scanned-probe experiments, while in the measurements reported here, the cantilever tip moves parallel to the vacuum-polymer interface, as sketched in Fig. 1(a). In the case of perpendicular tip motion, the tip-sample capacitance and hence the tip charge qc can vary significantly over the period of the probe’s motion, while for parallel tip motion, qc may be assumed to be constant over the period of the probe’s motion. Yazdanian et al. recently reported an approach to calculating both cantilever frequency noise and noncontact friction in terms of the dielectric function, film thickness, and probe height.19 Calculations in Ref.19 were performed for the case of parallel tip motion, and the frequency jitter was found to be driven by fluctuations in the electric field gradient at the tip.
FIG. 1.
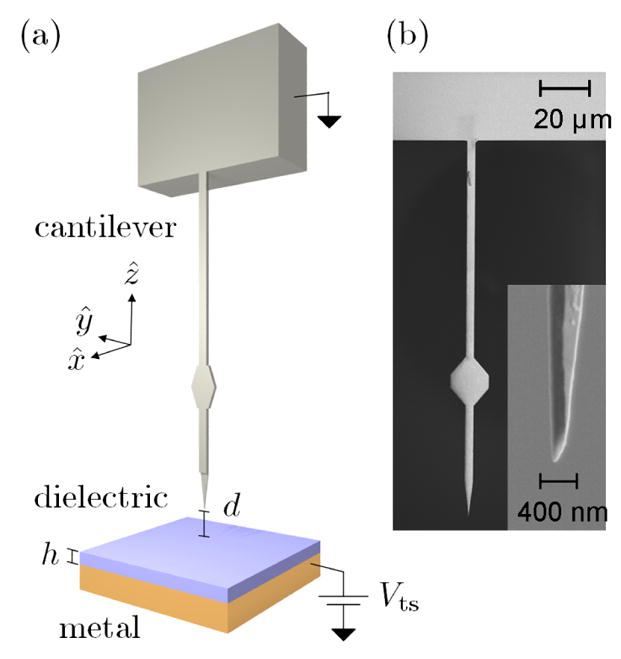
Experimental set-up. (a) A charged cantilever tip oscillates in the x direction, parallel to the sample surface, at a height z = d above the surface of a dielectric sample of thickness h. The tip is charged by applying a voltage Vts between the tip and a metal film under the sample. (b) Scanning electron micrograph of a representative cantilever. The hexagonal pad acts as a target for an optical fiber interferometer. Inset: Close-up of the cantilever tip. Here the cantilever is shown prior to coating its end with platinum using a shadow mask.
Generalizing this analysis to the case of perpendicular tip motion, we have found that the frequency jitter includes contributions from three mechanisms: (1) voltage fluctuations that couple to the second spatial derivative of the capacitance, as invoked by Israeloff and coworkers,33–35 (2) electric field fluctuations that couple to the gradient of the capacitance, and (3) fluctuations in the electric field gradient that couple to the tip charge as for the parallel geometry. If the spatial derivatives of the capacitance are negligible as for the case of the parallel geometry, only mechanism (3) remains. Thus frequency jitter with the perpendicular geometry of Refs. 33–35 and frequency jitter with the parallel geometry as reported here are actually different experimental observables with different information content.
For the configuration of Figure 1(a), we have shown19 that the power spectrum of cantilever frequency fluctuations Pδfc(f) can be written as
| (2) |
where we define the power spectrum as
| (3) |
Here kc is the cantilever spring constant and CδExx (t) ≡ 〈δExx(t)δExx(0)〉 is the equilibrium autocorrelation function of fluctuations in Exx ≡ ∂Ex/∂x, the electric field gradient at the probe tip. In Ref. 19 we evaluated CδExx (t) from a dielectric continuum model for the polymer film and found
| (4) |
| (5) |
| (6) |
The jitter power spectrum is related here to the tip-sample separation d, the sample thickness h, the cantilever force constant kc and frequency fc in the absence of the sample, the tip charge qc, and the complex-valued relative dielectric function of the sample ε(2πf). For known tip charge, qc, this expression contains no free parameters. The purpose of this paper is to make a rigorous comparison of eqs 4–6 to new measurements of the power spectrum of cantilever frequency fluctuations over polymer films of various composition as a function of height and film thickness.
Measurements were carried out with custom-fabricated silicon microcantilevers11,12,17 whose sensitivity is two orders of magnitude higher than commercial cantilevers. Figure 1(b) shows a scanning electron micrograph of a representative cantilever, made from single-crystal silicon. The cantilevers are L = 275 μm long, 7 μm wide, and 340 nm thick, with spring constants between 7.6×10−4 and 1.7×10−3 N/m, resonance frequencies between 5 and 6 kHz, and mechanical quality factors as high as 15000 in high vacuum (P = 10−6 mbar). By offsetting the optical mask during lithography,11,17 a tip width as small as ~100 nm could be achieved. The leading edge of the cantilever was thinned to 150 nm and coated with 15 nm of platinum using a shadow mask.11,17 The resulting metallized cantilever tip is reasonably well approximated as a sphere. A tip before metallization can be seen in the inset of Fig. 1(b).
The spring constant kc of each cantilever was measured by analyzing thermomechanical position fluctuations using the equipartition theorem.36 The mean-square amplitude of cantilever thermal vibrations, 〈 〉, was estimated from the area under an averaged position-fluctuation power spectrum, calculated from 25 transients lasting 25 s each. The spring constant was then computed as .
Films were prepared of three polymers: poly(methyl methacrylate), poly(vinyl acetate), and polystyrene (Table I). The polymers were spin-cast from toluene onto epitaxial Au(111)-on-mica substrates (Agilent; Part No. N9805B-FG) and their thickness measured by profilometry. The samples were then transferred to a high vacuum oven (P = 10−6 mbar) and annealed at Tg + 10°C for 12 hours to remove solvent and water. For Tg, we used glass transition temperatures published for polymers with molecular weights similar to ours.37–39 Dielectric spectra, ε(2πf), for PMMA and PVAc were measured in 440 nm thick polymer films using an impedance analyzer (Hewlett Packard; Model No. 4192 A LF).40 The spectrum of polystyrene was kindly provided by Professor Ranko Richert.41
TABLE I.
Polymers studied. Here εr is relative dielectric constant, Mw is weight-averaged molecular weight, Mw/Mn is polydispersity, Tg is glass transition temperature from Refs. 37–39, and S.P.P. stands for Scientific Polymer Products.
| mat’l | εr | Mw [kDa] | Mw/Mn | Tg [°C] | Mfgr. and Catalog No. |
|---|---|---|---|---|---|
| atactic PMMA | 3.9 | 145 | 1.05 | 115 | S.P.P. 942 |
| atactic PVAc | 3.4 | 140 | 3.1 | 35 | Aldrich 387924-500G |
| PS | 2.5 | 151 | 1.09 | 108 | S.P.P. 849 |
To study each film, a cantilever was mounted to a custom-built scanning probe microscope.19,40 Cantilever displacement was detected with an optical fiber interferometer operating at 1310 nm. The microscope had two levels of vibration isolation – custom-made stainless steel bellows and a commercial vibration isolation stage (Minus-k 250BM-3). A commercial nanopositioner (Attocube ANPz 51) was used to bring the cantilever into contact with the surface and to scan the tip-sample separation. The film surface (d = 0) was located by measuring cantilever quality factor Q, via a ringdown measurement, at various heights d; the surface was defined within ±2 nm as the height at which Q extrapolated to zero.16,17,40 This noncontact protocol for locating the surface was validated by bringing the cantilever towards the surface and watching with the interferometer for a characteristic dc displacement that occurs at d = 0 when the cantilever buckles upon touching the surface.
A cantilever was then brought to a calibrated distance d over a film and its tip charged by applying a voltage Vts between the cantilever and the gold of the substrate. To measure temporal fluctuations in the cantilever resonance frequency over a film, the cantilever was driven into self oscillation using a custom-built analog positive feedback loop.42 The resulting oscillation x(t) was digitized and passed through a 10th order Butterworth bandpass filter (center frequency fc, bandwidth ffilt = 2 × 2100 Hz). The instantaneous cantilever frequency fc(t) was determined from the filtered signal by means of a software frequency demodulator, as described in detail in the Supplement of Ref. 19. Averaged power spectra Pδfc of cantilever frequency fluctuations δfc(t) = fc(t) − 〈fc〉 were determined using Eq. 3; each spectrum was computed from, typically, Navg = 50 frequency transients lasting Tacq = 25s each. Bandpass filtering x(t) has the effect of lowpass filtering Pδfc. Using a high order filter is important to avoid contamination of low f Fourier components in Pδf by aliasing of instrument noise present on either side of fc in x(t). The non-contact friction coefficient was measured17 by recording the cantilever ringdown time τ and calculating .
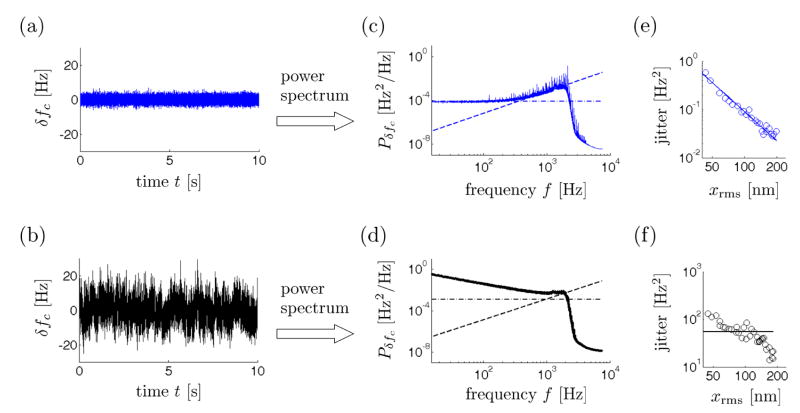
The data of Figure 2(a–b) confirm33–35 that a charged cantilever does indeed exhibit increased frequency fluctuations near the surface of a polymer film. The sample is a 200 nm thick film of PMMA. As the tip-sample separation is decreased from d = 2000 nm to d = 25 nm, the root-mean-square fluctuation in cantilever frequency increases over fourfold. With an ultrasensitive cantilever, this increase in frequency noise due to fluctuations in the film can be easily distinguished even with only 1 s of acquisition.
FIG. 2.
Cantilever frequency fluctuations over a 200 nm thick film of PMMA at large tip-sample separation (d = 2000 nm, upper panels, blue data) and small tip-sample separation (d = 25 nm, lower panels, black data). (a, b) Cantilever frequency fluctuations in a 2100 Hz bandwidth centered at the cantilever frequency. (c, d) Power spectra of cantilever frequency fluctuations. The lines show contributions to the cantilever frequency-fluctuation power spectra from detector noise (dashed) and thermomechanical position fluctuations (dot-dashed). Here fc = 4158Hz, kc = 0.87mN/m, and Q(d = 2000nm) = 4700 while Q(d = 25nm) = 500. The dot-dashed lines were computed using these values and eq 7. The dashed line was computed from eq 8 using the measured detector noise (d = 2000 nm) = 3.3 × 10−6 nm2/Hz and (d = 25 nm) = 6.6 × 10−6 nm2/Hz. (e, f) Cantilever frequency jitter in a 100 Hz bandwidth vs. root-mean-square cantilever amplitude. In (a–d), the cantilever amplitude was xrms = 70 nm-rms. Throughout, the tip-sample voltage was Vts = φ + 0.5 V where φ = − 0.1 V is the measured contact potential difference between the tip and the underlying gold substrate.
To better distinguish polymer-induced cantilever frequency noise from contributions originating in cantilever thermomechanical position fluctuations and detector noise, it is useful to examine the power spectrum of cantilever frequency fluctuations. In Fig. 2(c) we show the power spectrum of cantilever frequency fluctuations, Pδfc (f) vs. f, at a height d = 2000nm over a 200 nm thick film of PMMA. The horizontal dot-dashed line is the contribution to frequency noise expected from thermomechanical position fluctuations19,42,43:
| (7) |
where xrms is the root-mean-square amplitude of the driven cantilever. The dashed line in the figure is the detector’s contribution to frequency noise19,42,43:
| (8) |
where is detector noise written in terms of an equivalent fluctuation of the cantilever displacement. In the absence of a sample (or at large tip-sample separations), we find cantilever frequency fluctuations to be dominated by thermomechanical position fluctuations and detector noise, as seen in Fig. 2(c). Equations 7 and 8 together account, quantitatively, for the entire power spectrum of cantilever frequency fluctuations apparent in Fig. 2(c) at large tip-sample separation.
At small tip-sample separations, in contrast, the power spectrum of cantilever frequency fluctuations is much larger than expected from thermomechanical and detector noise alone. In Fig. 2(d) we show the power spectrum of cantilever frequency fluctuations at a height d = 25nm. Near f = 0, the frequency fluctuations have a power spectrum over 102 times larger than the thermomechanical and detector contributions. We attribute this excess frequency noise to tip-sample interactions. At d = 25 nm, with our ultrasensitive cantilevers, we can resolve Fourier components in sample-induced frequency noise up to a frequency of approximately f = 500Hz, a factor of twenty higher than was demonstrated in Ref. 35.
Having established that polymer-induced frequency fluctuations are large and detectable with excellent signal-to-noise using an ultrasensitive cantilever oscillating parallel to the sample surface, we are now ready to explore the dependence of frequency fluctuations on tip charge, tip-sample separation, and film composition and thickness. We will summarize these studies by plotting the frequency integral of the power spectrum of frequency fluctuations,
| (9) |
We refer to this quantity as “jitter”. In the hypothetical limit that fL → 0 and fU → ∞, this quantity equals 〈(δfc)2〉. We set the lower cutoff frequency to fL = 0 Hz except when comparing theory to experiment, in which case we set fL = 5 Hz to reject low-frequency noise in the measured dielectric function. The upper cutoff frequency, fU = 100 Hz, is necessary to reject high-frequency instrument noise present in the measurements (Fig. 2(c–d)).
In Fig. 2(e) we plot jitter at height d = 2000 nm over a PMMA film as a function of cantilever amplitude. The solid line on the log-log plot has slope −2, confirming that jitter ∝ , as expected from eq 7. The jitter vs. cantilever amplitude at small tip-sample separation, d = 25nm, can be seen in Fig. 2(f). At small cantilever amplitude, the jitter is approximately constant (solid line), in agreement with the continuum model of dielectric fluctuations used to derive eqs 4–6. At large xrms, however, the jitter in Fig. 2(f) decreases substantially. By introducing a wavevector-dependent dielectric constant, ε○(k, ω), into the theory of Ref. 19, we believe it should be possible to use data like that in Fig. 2(f) to obtain information about spatial-temporal correlations in the sample’s dielectric function — an exciting possibility.
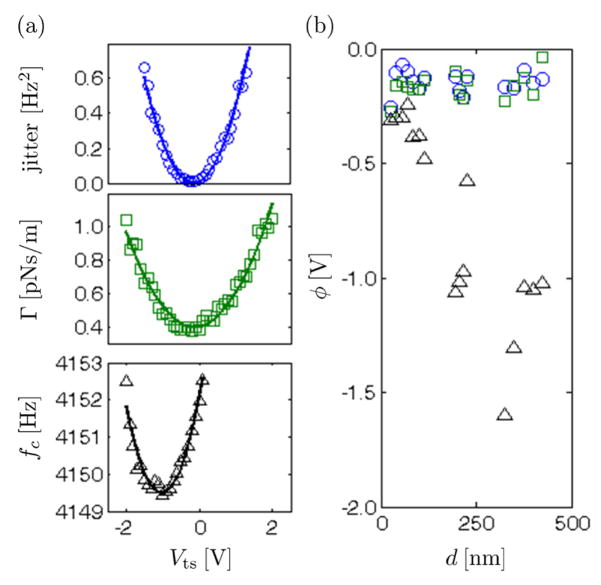
In Fig. 3 we plot frequency jitter vs. tip-sample voltage for a cantilever at various heights over a PMMA film. The applied voltage puts a charge on the tip qc = C(Vts − φ), where C is the tip-sample capacitance and φ is the difference in contact potential between tip and sample. From eqs 2 and 9 we expect jitter ∝ C2(Vts − φ)2. We can see in Fig. 3 that the jitter is indeed a quadratic function of the applied tip voltage. By fitting the data to a parabola we can extract the contact potential φ. We note that measured φ is not quite independent of tip-sample separation as one might expect; we will return to this observation below in discussing Fig. 6. That jitter depends quadratically on voltage confirms a key assumption of our theory19 — that cantilever frequency fluctuations can be calculated using linear-response theory.
FIG. 3.
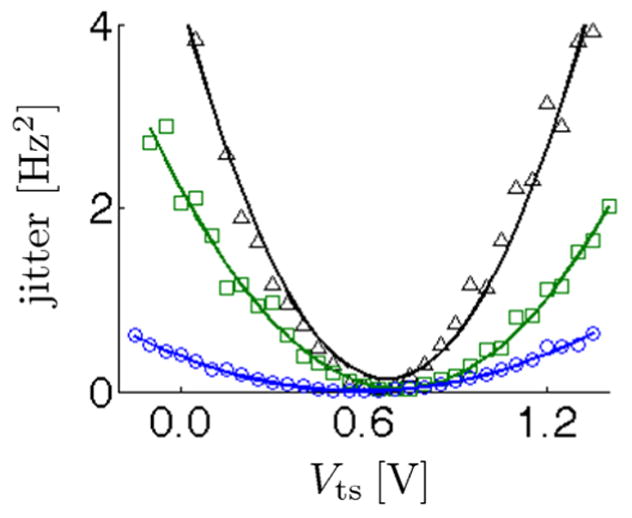
Frequency jitter vs. tip-sample voltage over a 466 nm thick PMMA film at various heights. Data (points) and parabola fits (lines) are shown for tip-sample heights of d = 75 nm (black triangles), d = 100 nm (green squares) and d = 250 nm (blue circles). The cantilever amplitude was xrms = 75 nm and the cutoff frequencies were fL = 0 Hz and fU = 100 Hz.
FIG. 6.
(a) Simultaneously-acquired jitter (blue circles), noncontact friction coefficient Γ (green squares), and cantilever frequency fc (black triangles) vs. tip-sample voltage Vts at a height d = 100 nm over a 200 nm thick film of PMMA. Solid-lines are parabolic fits. (b) The voltage at the parabola minimum, φ, as measured from the jitter (blue circles), noncontact friction coefficient (green squares), and frequency (black triangles) parabolas. The tip amplitude was xrms = 70nm-rms throughout; jitter was measured in a 100 Hz bandwidth (fL = 0 Hz and fU = 100 Hz).
We now compare the measured Pδfc to eq 4. In order to calculate qc, we approximate the charged tip of the cantilever as a sphere of radius R located a distance d above a dielectric slab of thickness h backed by a conductor.19,44,45 We use eqs 6.5 and 6.6 in Ref.19 to calculate the tip-sample capacitance C and then calculate the tip charge qc from C, the measured contact potential φ, and the applied tip-sample voltage Vts. We take the tip radius to be R = 70 nm, based on the scanning electron micrograph in Fig. 1(b).
In Fig. 4 we compare the measured and calculated Pδfc at a height d = 100 nm above a 200 nm thick PMMA film. The measured and calculated curves agree within better than a factor of two over more than two decades of frequency. A Pδfc ∝ 1/f line is plotted for comparison. We see that, in this experiment, the cantilever frequency-fluctuation power spectrum is well approximated as a 1/f spectrum for frequencies in the 5 to 500 Hz range, with small deviations from 1/f behavior apparent only below f ≈ 5 Hz.
FIG. 4.
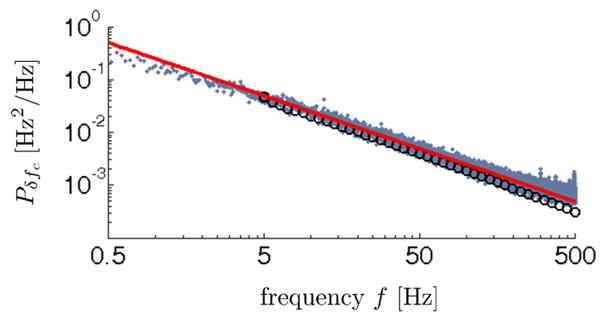
Observed and calculated power spectrum of cantilever frequency fluctuations at height d = 100 nm over a 200 nm thick PMMA film. The small blue-gray dots are the observed spectrum. The large black circles are the spectrum calculated from eqs 4–6, the measured dielectric spectrum, and the tip-sample capacitance model discussed in the text. The red line shows a 1/f spectrum, as a guide to the eye. Applied voltage Vts = 0.5 V + φ with φ = −0.1 V; and xrms = 70 nm-rms, Navg = 50, and Tacq = 25 s.
This finding is in qualitative agreement with the Pδfc ∝ ε″(f)/f behavior predicted by Walther et al.,33 given that the measured ε″ for our PMMA sample is approximately constant from f = 5 Hz to 500 Hz. Equations 4–6 also predict Pδfc ε″(f)/f for the limiting case ε″ (f) ≪ 1, valid for our measurements. Equations 4–6 predict quantitatively the absolute size of the observed frequency fluctuations
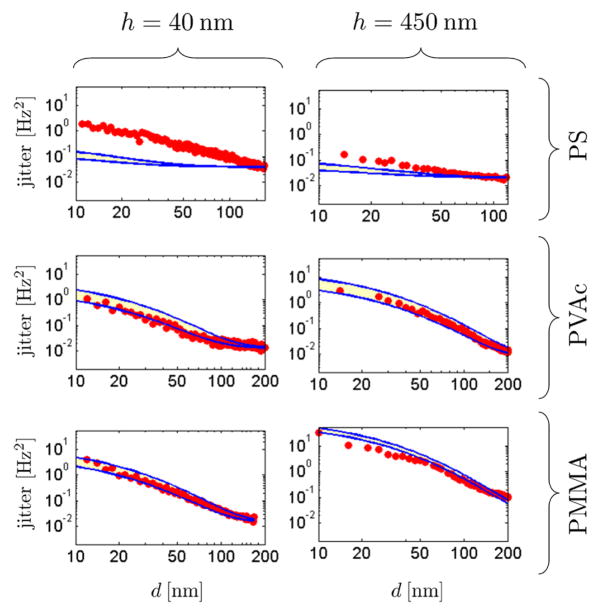
In Fig. 5 we use the measured contact potential, estimated capacitance, measured dielectric spectrum, and eqs 4 and 9 to predict jitter in a bandwidth from 5 to 100 Hz as a function of tip-sample separation d. In computing tip charge, we found it necessary to account for the height dependence of the contact potential φ shown in Fig. 3, as follows. In each sample φ was measured at 4 to 10 selected heights. Over the six samples studied at heights from d = 10 nm to over 200 nm, the observed φ ranged from 0.29 V to 0.95 V. In any one sample, a variation of ≤ 0.2 V was seen. In each sample, a high, low, and average contact potential (φhigh, φlow, and φavg) were identified. The applied voltage was set to Vts ≈ 0.5 V + φavg. To account for the observed variation in contact potential, for each sample two theory curves are calculated: one with φ = φlow and one with φ = φhigh. In Fig. 5 the region between these two curves is colored yellow.
FIG. 5.
Dependence of jitter on tip-sample separation for six polymer films. The film composition and thickness are indicated in the figure. The red dots are the jitter obtained from the measured power spectrum using fL = 5 Hz and fU = 100 Hz. The yellow regions are the predicted jitter, calculated as discussed in the text. The applied voltage was Vts ≈ 0.5 V + φavg where φavg is the height-averaged contact potential, measured independently in each sample. The cantilever amplitude was xrms = 70 nm-rms, Navg = 50, and Tacq = 1 s.
The results for six samples are shown in Fig. 5: films of PS (upper row), PVAc (middle row), and PMMA (lower row) of thickness h = 40nm (left column) and 450nm (right column). Theory correctly predicts the magnitude of the observed jitter and its dependence, qualitatively, on distance. Comparing films of the same composition, theory also predicts correctly whether the thick film or the thin film will have the larger jitter at close separation. This prediction cannot be made without a detailed calculation: the electric field gradient fluctuations are largest over the thick film, but at fixed tip-sample voltage the tip charge is less over the thick film and so the fluctuations couple less well to the cantilever; differences in kc must also be accounted for.
The agreement between theory and experiment is poorest in polystyrene, where theory underestimates the jitter observed at close separations by a factor of three in the thick film and by a factor of ten in the thin film. It is not surprising that of the three samples, polystyrene would show the worst agreement. The ε″ in polystyrene is very small and notoriously difficult to measure, and is likely therefore more sensitive to sample preparation than either PMMA and PVAc. Although we were able to obtain ε′ and ε″ for polystyrene of molecular weight comparable to ours,41 the sample was not identical to that used in our cantilever measurements. Neither ε′ nor ε″ for PS depend significantly on frequency over the relevant range. Treating these constants as adjustable parameters does not yield a dielectric function that reproduces the PS data for both thin and thick films with the same level of agreement shown for PVAc and PMMA. This suggests that dielectric fluctuations in the thin PS film are not well represented by bulk dielectric relaxation processes alone.
For the four PMMA and PVAc films, where ε′ and ε″ could be measured in identically-prepared samples, the measured and predicted jitter are in quantitative agreement. The magnitude of the jitter and its dependence on tip-sample separation is correctly predicted over two decades of jitter in both of these samples. The agreement between theory and measurement in Fig. 5 confirms33–35 that the jitter measurement probes low frequency polymer motions. In PMMA, for example, these low frequency motions include hindered rotations of polar side groups.46
The ability to detect minute electric field gradient fluctuations is greatly enhanced by using an ultrasensitive cantilever. To demonstrate this, let us define a spectral density of electric field gradient fluctuations PδExx by analogy with eq 3 and rewrite Pδfc (eq 2) in terms of PδExx. To determine the thermally-limited minimum detectable electric field gradient, we set Pδfc equal to (eq 7),
| (10) |
where we have written the result in terms of the dissipation constant using Γ = kc=2πfcQ. For a commercial electric force microscope cantilever, Γ = 1.5 × 10−9 Ns/m (fc = 75 kHz, kc = 3.5 N/m, and Q = 5 × 103). For an ultrasensitive cantilever, the friction coefficient can be as good as17 Γ = 5 × 10−13 Ns/m (fc = 7.4 kHz, kc = 0.7 mN/m, and Q = 3.1×104). We conclude that the ultrasensitive cantilever can resolve a 3000-fold smaller fluctuation PδExx than can a commercial cantilever operated in vacuum with the same tip charge and amplitude.
Above we inferred the contact potential φ from a plot of jitter vs. voltage acquired at selected tip-sample separations. We explored a much quicker, and in principle equivalent, method for measuring φ: recording frequency as a function of applied tip voltage. The voltage dependence of the non-contact friction coefficient was measured simultaneously as a control.
Figure 6(a) shows a plot of jitter, noncontact friction coefficient Γ, and frequency fc over a PMMA film as a function of tip-sample voltage Vts. The contact potential obtained by fitting the jitter vs. voltage data to a parabola is φjitter = − 0.14±0.02V. Fitting the Γ vs. Vts curve to a parabola gives a statistically equivalent result: φΓ = − 0.13±0.04V. While the cantilever frequency is also observed to be a parabolic function of voltage, the contact potential inferred from the fc vs. Vts curve is quite different: φfc = − 1.02 ± 0.03 V, twenty four standard deviations away from φjitter and φΓ.
Parabolas of jitter, Γ, and frequency fc were used to infer φjitter, φΓ, and φfc as a function of tip-sample separation for d = 25 to 500 nm over the PMMA sample. The results are summarized in Fig. 6(b). The contact potentials inferred from jitter and noncontact friction agreed within 0.1 V over the range of d and were essentially independent of tip-sample separation. While φfc agrees with φjitter and φΓ at very small tip-sample separations, it differs from φjitter and φΓ by as much as 1.5 V at a few hundred nanometer separation.
A similarly large height-dependent shift in contact potential has been seen by Rast et al.31 in measurements of the frequency of an ultrasensitive cantilever over a gold film in ultrahigh vacuum. This shift was ascribed31 to either patch charges47 on the gold or to surface contaminants. Neither hypothesis explains the discrepancy between φfc and φjitter or φΓ seen in Fig. 6. Silveira et al. have suggested that in an experiment with the cantilever oscillating perpendicular to the surface at constant voltage, the force (e.g., displacement) and frequency parabolas could have different minima in the presence of a height-dependent contact potential.48 An alternative hypothesis is that the frequency measurement is more sensitive to the presence of charge on the silicon body of the cantilever, which has a different work function from the platinum tip, than are the measurements of friction and jitter.
Figures 4 and 5 are the central results of this letter. They show that our linear-response theory19 accurately predicts the dependence of cantilever frequency noise on polymer composition, tip-sample separation, and film thickness, as well as predicting the shape of the frequency-fluctuation power spectrum. The inputs to the theory — the polymer’s low-frequency dielectric spectrum and the tip diameter, used to estimate the capacitance — were measured independently. The comparison to theory thus involves no free parameters. Taken together with the results of Refs. 17 and 18, the data presented here suggest that a single unified theory describes noncontact friction (due to electric field fluctuations) and frequency jitter (due to electric field gradient fluctuations) in thin polymer films.
Cantilever dissipation probes only the Fourier component of electric field fluctuations at the cantilever frequency.16,17,40 In contrast, the entire low frequency spectrum of electric field gradient fluctuations is encoded in cantilever frequency noise.33–35,49 Our results show that ultrasensitive cantilevers are a particularly broadband detector, capable of quantifying electric field gradient fluctuations from below 10−2 Hz to nearly 103 Hz. Operating the cantilever in the parallel geometry of Fig. 1 makes it possible to straightforwardly interpret frequency noise in terms of an electric field gradient fluctuation. Our findings motivate using an ultrasensitive cantilever to test microscopic models of other fluctuations, such as charge fluctuations in heterogeneous electronic materials.
Supplementary Material
Acknowledgments
We thank Professor Ranko Richert for a polystyrene dielectric spectrum. SMY acknowledges the National Science Foundation through the Cornell Center for Nanoscale Systems (EEC-0117770 and EEC-0646547) and grants DMR-0134956 and DMR-0706508. NH acknowledges the U.S. Army Research Office Multi-University Research Initiative (W911NF-05-1-0403) and the Principality of Liechtenstein. SK acknowledges the National Institutes of Health (5R01GM-070012) and the Society of Analytical Chemists of Pittsburgh. RFL acknowledges the National Science Foundation (CHE-0413992 and CHE-0743299). JAM acknowledges the National Institutes of Health (5R01GM-070012), the Army Research Office Multi-University Research Initiative (W911NF-05-1-0403), and the National Science Foundation (DMR-0134956). This work was performed in part at the Cornell NanoScale Science and Technology Facility, a member of the National Nanotechnology Infrastructure Network, supported by the National Science Foundation (ECS-0335765).
Footnotes
Supporting Information Available: Details of the protocol used to determine cantilever spring constant; dielectric spectroscopy data; and data ruling out alternative frequency fluctuation mechanisms.19 This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Binnig G, Quate C, Gerber C. Phys Rev Lett. 1986;56:930 –933. doi: 10.1103/PhysRevLett.56.930. [DOI] [PubMed] [Google Scholar]
- 2.Martin Y, Williams C, Wickramasinghe H. J Appl Phys. 1987;61:4723 – 4729. [Google Scholar]
- 3.Frisbie C, Rozsnyai L, Noy A, Wrighton M, Lieber C. Science. 1994;265:2071 – 2074. doi: 10.1126/science.265.5181.2071. [DOI] [PubMed] [Google Scholar]
- 4.Martin Y, Wickramasinghe H. Appl Phys Lett. 1987;50:1455 –1457. [Google Scholar]
- 5.Rugar D, Mamin H, Guethner P, Lambert SE, Stern J, McFadyen I, Yogi T. J Appl Phys. 1990;68:1169 – 1183. [Google Scholar]
- 6.Martin Y, Abraham D, Wickramasinghe H. Appl Phys Lett. 1988;52:1103 –1105. [Google Scholar]
- 7.Nonnenmacher M, O’Boyle M, Wickramasinghe H. Appl Phys Lett. 1991;58:2921 – 2923. [Google Scholar]
- 8.Kalinin S, Gruverman A. Scanning Probe Microscopy: Electrical and Electromechanical Phenomena at the Nanoscale. Springer Verlag; New York: 2005. [Google Scholar]
- 9.Crider PS, Majewski MR, Zhang J, Ouckris H, Israeloff NE. Appl Phys Lett. 2007;91:013102. [Google Scholar]
- 10.Crider PS, Majewski MR, Zhang J, Ouckris H, Israeloff NE. J Chem Phys. 2008;128:044908. doi: 10.1063/1.2825301. [DOI] [PubMed] [Google Scholar]
- 11.Stowe TD, Yasumura K, Kenny TW, Botkin D, Wago K, Rugar D. Appl Phys Lett. 1997;71:288 – 290. [Google Scholar]
- 12.Jenkins NE, DeFlores LP, Allen J, Ng TN, Garner SR, Kuehn S, Dawlaty JM, Marohn JA. J Vac Sci Technol B. 2004;22:909 – 915. [Google Scholar]
- 13.Rugar D, Budakian R, Mamin HJ, Chui BW. Nature. 2004;430:329 – 332. doi: 10.1038/nature02658. [DOI] [PubMed] [Google Scholar]
- 14.Kuehn S, Hickman SA, Marohn JA. J Chem Phys. 2008;128:052208. doi: 10.1063/1.2834737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Stowe TD, Kenny TW, Thomson DJ, Rugar D. Appl Phys Lett. 1999;75:2785 – 2787. [Google Scholar]
- 16.Stipe BC, Mamin HJ, Stowe TD, Kenny TW, Rugar D. Phys Rev Lett. 2001;8709:6801. doi: 10.1103/PhysRevLett.86.2874. [DOI] [PubMed] [Google Scholar]
- 17.Kuehn S, Loring RF, Marohn JA. Phys Rev Lett. 2006;96:156103. doi: 10.1103/PhysRevLett.96.156103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kuehn S, Marohn JA, Loring RF. J Phys Chem B. 2006;110:14525 – 14528. doi: 10.1021/jp061865n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yazdanian SM, Marohn JA, Loring RF. J Chem Phys. 2008;128:224706. doi: 10.1063/1.2932254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Denk W, Pohl DW. Appl Phys Lett. 1991;59:2171 – 2173. [Google Scholar]
- 21.Hoffmann B, Houbertz R, Hartmann U. Appl Phys A. 1998;66:S409 – S413. [Google Scholar]
- 22.Park JY, Ogletree DF, Thiel PA, Salmeron M. Phys Rev B. 2007;76:064108. [Google Scholar]
- 23.Qi Y, Park JY, Hendriksen BLM, Ogletree DF, Salmeron M. Phys Rev B. 2008;77:184105. [Google Scholar]
- 24.Grütter P, Liu Y, LeBlanc P, Durig U. Appl Phys Lett. 1997;71:279 – 281. [Google Scholar]
- 25.Liu Y, Grütter P. J Appl Phys. 1998;83:5922 – 5926. [Google Scholar]
- 26.Volokitin A, Persson B. Phys Rev Lett. 2003;91:106101. doi: 10.1103/PhysRevLett.91.106101. [DOI] [PubMed] [Google Scholar]
- 27.Zurita-Sanchez J, Greffet J, Novotny L. Phys Rev A. 2004;69:022902. [Google Scholar]
- 28.Chumak A, Milonni P, Berman G. Phys Rev B. 2004;70:085407. [Google Scholar]
- 29.Volokitin A, Persson B. Phys Rev Lett. 2005;94:086104. doi: 10.1103/PhysRevLett.94.086104. [DOI] [PubMed] [Google Scholar]
- 30.Volokitin A, Persson B, Ueba H. Phys Rev B. 2006;73:165423. [Google Scholar]
- 31.Rast S, Gysin U, Ruff P, Gerber C, Meyer E, Lee D. Nanotechnology. 2006;17:S189 – S194. doi: 10.1088/0957-4484/17/7/S15. [DOI] [PubMed] [Google Scholar]
- 32.Labaziewicz J, Ge Y, Leibrandt DR, Wang SX, Shewmon R, Chuang IL. Phys Rev Lett. 2008;101:180602. doi: 10.1103/PhysRevLett.101.180602. [DOI] [PubMed] [Google Scholar]
- 33.Walther LE, Russell EV, Israeloff NE, Gomariz HA. Appl Phys Lett. 1998;72:3223 – 3225. [Google Scholar]
- 34.Russell EV, Israeloff NE, Walther LE, Gomariz HA. Phys Rev Lett. 1998;81:1461 –1464. [Google Scholar]
- 35.Russell EV, Israeloff NE. Nature. 2000;408:695 – 698. doi: 10.1038/35047037. [DOI] [PubMed] [Google Scholar]
- 36.Hutter J, Bechhoefer J. Rev Sci Instrum. 1993;64:1868 –1873. [Google Scholar]
- 37.Keddie J, Jones R, Cory R. Faraday Discuss. 1994;98:219 –230. [Google Scholar]
- 38.Fukao K, Uno S, Miyamoto Y, Hoshino A, Miyaji H. J Non-Cryst Solids. 2002. pp. 307–310.pp. 517–523. [Google Scholar]
- 39.Wada Y, Hirose H, Asano T, Fukutomi S. J Phys Soc Japan. 1959;14:1064 –1072. [Google Scholar]
- 40.Kuehn S. Ph D Thesis. Cornell University; New York: 2007. Force-gradient detected nuclear magnetic resonance and the origins of noncontact friction. [Google Scholar]
- 41.Richert R. (personal communication) [Google Scholar]
- 42.Albrecht TR, Grütter P, Horne D, Rugar D. J Appl Phys. 1991;69:668 – 673. [Google Scholar]
- 43.Obukhov Y, Fong KC, Daughton D, Hammel PC. J Appl Phys. 2007;101:034315. [Google Scholar]
- 44.Terris BD, Stern JE, Rugar D, Mamin HJ. Phys Rev Lett. 1989;63:2669 – 2672. doi: 10.1103/PhysRevLett.63.2669. [DOI] [PubMed] [Google Scholar]
- 45.Cherniavskaya O, Chen L, Weng V, Yuditsky L, Brus LE. J Phys Chem B. 2002;107:1525 – 1531. [Google Scholar]
- 46.Bergman R, Alvarez F, Alegria A, Colmenero J. J Chem Phys. 1998;109:7546 – 7555. [Google Scholar]
- 47.Burnham NA, Colton RJ, Pollock HM. Phys Rev Lett. 1992;69:144 –147. doi: 10.1103/PhysRevLett.69.144. [DOI] [PubMed] [Google Scholar]
- 48.Silveira WR, Muller EM, Ng T-N, Dunlap DH, Marohn JA. In: Scanning Probe Microscopy: Electrical and Electromechanical Phenomena at the Nanoscale. Kalinin SV, Gruverman A, editors. II. Springer; New York: 2007. [Google Scholar]; Chapter “High-sensitivity electric force microscopy of organic electronic materials and devices”. :788. [Google Scholar]
- 49.Crider PS, Israeloff NE. Nano Lett. 2006;6:887 – 889. doi: 10.1021/nl060558q. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.