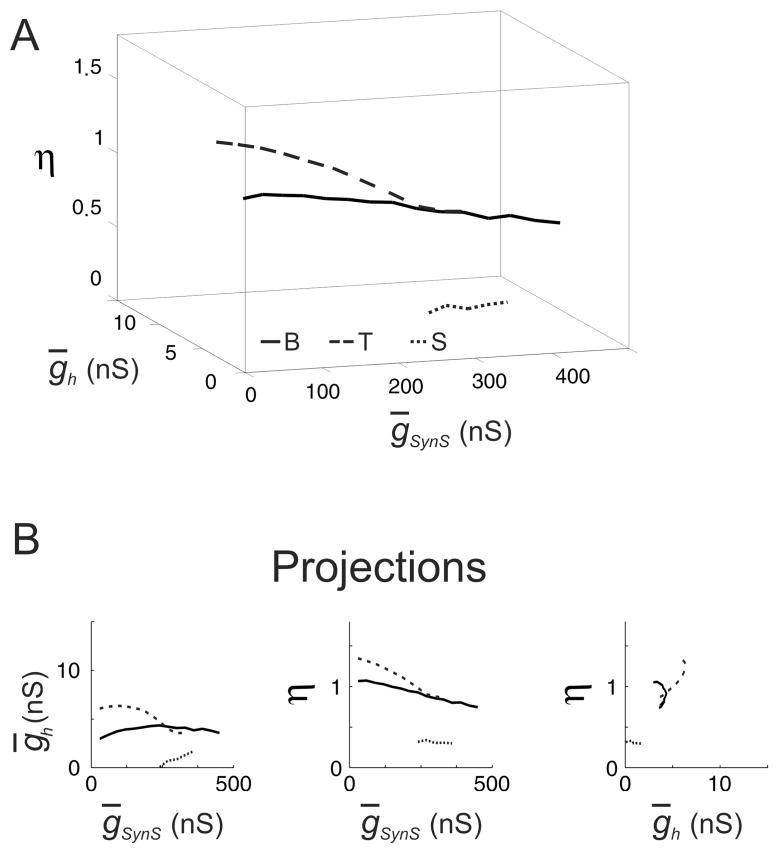
FIG. 4.
The isocurves of the constant period and spike frequency of the HCO model for three networks with the same target values of the period and spike frequency, C-isocurves. The network models were different in the parameters of the leak current, (ḡL, EL), which were (9.9 nS, −63.5 mV), solid curve, (8 nS, −60 mV), dashed curve, and (9.9 nS, −65.8 mV), dotted curve. As in Fig. 3, these three pairs of parameters corresponded to three types of endogenous neuronal dynamics, bursting, tonic spiking, and silence, provided all the other parameters of the model had canonical values. The target values of the period and frequency were 7.91 sec and 8.82 Hz for the all three networks. (A) The C-isocurves in the space of ḡSynS, ḡh, and η Note, that the three isocurves do not cross at the point, corresponding to the canonical values ḡSynS = 150 nS, ḡh = 4nS, and η = 1. The HCOs of tonically spiking neurons and silent neurons could have the same values of period and frequency for the canonical values of ḡSynS, ḡh, and η as the HCO composed of bursters. In fact, in the case of tonically spiking neurons, there were no values of ḡh, and η for which the HCO model could have target values of the period and burst frequency for ḡSynS = 150 nS. (B) Planar projections of the isocurves. Note, that the dependence between ḡSynS and η was qualitatively the same for all the three types of networks: η decreased proportionally to the increase of ḡSynS. However, the dependence between ḡSynS and η for the tonically spiking neurons shifted to smaller values of η. Note that a range of ḡh which could be tolerated by the network of tonically spiking neurons, was smaller in this case compared to Fig. 3.