Imaging Electric Properties of Biological Tissues by RF Field Mapping in MRI

Abstract

The electric properties (EPs) of biological tissue, i.e., the electric conductivity and permittivity, can provide important information in the diagnosis of various diseases. The EPs also play an important role in specific absorption rate (SAR) calculation, a major concern in high-field Magnetic Resonance Imaging (MRI), as well as in non-medical areas such as wireless-telecommunications. The high-field MRI system is accompanied by significant wave propagation effects, and the radio frequency (RF) radiation is dependent on the EPs of biological tissue. Based on the measurement of the active transverse magnetic component of the applied RF field (known as B₁-mapping technique), we propose a dual-excitation algorithm, which uses two sets of measured B₁ data to noninvasively reconstruct the electric properties of biological tissues. The Finite Element Method (FEM) was utilized in three-dimensional (3D) modeling and B₁ field calculation. A series of computer simulations were conducted to evaluate the feasibility and performance of the proposed method on a 3D head model within a transverse electromagnetic (TEM) coil and a birdcage (BC) coil. Using a TEM coil, when noise free, the reconstructed EP distribution of tissues in the brain has relative errors of 12% ∼ 28% and correlated coefficients of greater than 0.91. Compared with other B₁-mapping based reconstruction algorithms, our approach provides superior performance without the need for iterative computations. The present simulation results suggest that good reconstruction of electric properties from B1 mapping can be achieved.

I. Introduction

The electric properties (EPs; conductivity σ and permittivity ε_r) of biological tissues at radio and microwave frequencies have been the subject of research for over four decades [1]. A comprehensive survey to date was conducted by Gabriel et al. [2-4], which covered a large selection of healthy tissue over a wide spectrum of frequencies (10Hz-20GHz). A few studies have also been conducted on EPs of a variety of cancerous tissue types at radio and microwave frequencies [5],[6],[7]. These studies have consistently shown that the EPs of cancerous tissues are three or more times greater than those of healthy tissue, and so it is anticipated that such EP information could be used in cancer detection. In addition, EPs are a determinant factor for the specific absorption rate (SAR), which is a major concern of safety in high-field Magnetic Resonance Imaging (MRI) systems and a critical problem in non-medical areas such as wireless-telecommunications.

In the past two decades, many efforts have been made to produce cross-sectional images of EPs in vivo by means of Electrical Impedance Tomography (EIT) [8-10] and its variants using magnetic induction (MIT) [11]. Both EIT and MIT are cost-effective and can provide dynamic information in regard to tissue EPs, but they are limited by low spatial resolution due to the surface measurements and the need to solve an ill-posed inverse problem. A technique called “Magnetic Resonance Electrical Impedance Tomography (MREIT)”, which is based on the Magnetic Resonance Current Density Imaging (MRCDI) technique [12] and measures current injection inducted MR phase shifts, has been pursued [13-16]. While MREIT eliminates the need to solve the ill-posed inverse problem and provides high spatial resolution in imaging electrical conductivity in vivo, it requires current injection into the body within an MRI scanner, which limits its applicability in medical applications. Another recently developed approach, Magnetoacoustic Tomography with Magnetic Induction (MAT-MI), offers the promise of obtaining high resolution tissue electrical conductivity profiles [17-20]. In MAT-MI, an object is placed in a static magnetic field and a pulsed magnetic field is applied to induce acoustic signals, which are then detected to reconstruct the tissue conductivity distribution. However, there have been no in vivo experiments reported so far.

Haacke et al. proposed a method of extracting EPs from MRI images [21]. They found that in 1.5T (and above) MRI systems, the wavelength of the radio frequency (RF) radiation was of the order of the body size, leading to a distortion of the RF field inside the irradiated object. By using an iterative sensitivity-matrix algorithm, these authors suggested that the EPs can be estimated using MRI images that reflect the disrupted RF profile. Wen later pointed out that the perturbation of the RF field in high-field MRI directly related to the conductivity and permittivity distribution within the sample, and a modified Helmholtz equation based non-iterative algorithm was proposed and tested in phantom experiments using 1.5T and 4.7T MRI [22]. Recently, using an iterative algorithm derived from Ampere's Law, Katscher et al. conducted an in vivo experiment using a 3T MRI system to image the EPs within a human head and leg [23], and named this approach “Magnetic Resonance Electric Properties Tomography (MREPT)”.

Signal intensity (SI) nonuniformity is distinct in high-field MRI systems. It can arise from a variety of factors, including imperfections in the scanner hardware and interactions between the magnetic field and biological tissues. Among these factors, electromagnetic (EM) interactions with the object have been shown to be the primary cause of SI nonuniformity for volume coils. It was reported that in 1.5T MRI systems, loaded birdcage (BC) coils had in-plane uniformity with 20% variation compared with as little as 1% variation when unloaded [24]. Through a series of experimental and simulation studies, it has been shown that the magnetic field distribution in the transverse plane of the coil is strongly dependent on the EPs of the biological tissues being studied [25]; moreover, the magnetic field distribution inside the RF coil at a high field can be studied and explained using Maxwell equations [26,27]. These findings have provided us with the mathematical framework to link EP distribution with MRI images.

The B₁-mapping technique [28-30] was developed to measure the rotating RF field components: the transmitted and received fields in RF coils. With the principle of reciprocity [31], the Cartesian transverse components of the RF magnetic field, H_x and H_y, can be derived. MREPT utilizes these two measurements to reconstruct the EP values within biological tissues, differing from other noninvasive imaging techniques in that no electrode mounting is required and no external energy is introduced into the body during MRI scanning. It can be performed using a standard MRI system with a regular volume coil, and its spatial resolution is determined by MRI images and the quality of the applied B₁-mapping technique [23].

In the present study, a new non-iterative dual-excitation MREPT algorithm to image the tissue EPs is proposed, and the finite element method (FEM) [32] is utilized in RF coil modeling and B₁ field calculation. The performance of the proposed MREPT algorithm is evaluated using a five-tissue 3D anatomically accurate head model, a shielded 12-rung birdcage, and a transverse electromagnetic (TEM) coil.

II. Dual-excitation MREPT approach

A. Computation in high-frequency time-harmonic EM field – the forward problem

The RF field excited in MRI coils can be treated as a time-harmonic EM field [27]. Assuming the object of interest to be isotropic, and using the generalized Ampere circuit law and Faraday's magnetic induction law in a time-harmonic EM field, Helmholtz equation can be derived as [33]

$$\nabla \times [{\mu }_r^{-1}·(\nabla \times \mathbf{\text{E}})]-k_0^2{\epsilon }_c·\mathbf{\text{E}}=-j\omega {\mu }_0{\mathbf{\text{J}}}_s$$ (1)

where E is the electric field vector, J_s the excitation current density in the coil, μ₀ the free space permeability, μ_r the relative permeability, ω the operating angular frequency, k₀ the vacuum wave number defined by $k_0=\omega \sqrt{{\epsilon }_0{\mu }_0}$ with ε₀ as the free space permittivity, and ε_c the complex permittivity ε_c = ε_rε₀ − jσ/ω with ε_r as the relative permittivity. Using the results of the electric field vector E, the magnetic field strength H can be obtained from [33]

$$\mathbf{\text{H}}=j{(\omega {\mu }_0{\mu }_r)}^{-1}·(\nabla \times \mathbf{\text{E}})$$ (2)

The finite element method is normally used to solve electromagnetic problems, and with its flexibility in grid size, FEM can deal with objects having irregular geometries with good accuracy. In the present study, all EM fields were calculated through (1) and (2) by means of FEM using ANSYS 11.0 (ANSYS, Inc., PA, USA) software with its “high-frequency harmonic EM analysis”, whereas the postprocessing of EM field data was completed using MATLAB 2008a (The Mathworks Inc., Natick, MA).

The B₁-mapping technique measures rotating RF field components: the transmitted ${\mathit{\text{H}}}_1^{+}$ and received field ${\mathit{\text{H}}}_1^{-}$ in RF coils. The principle of reciprocity [31] links magnetic field components in Cartesian and rotating frames via

$$\{\begin{array}{c}{\mathit{\text{H}}}_1^{+}=(H_x+j{H}_y)/2\\ {\mathit{\text{H}}}_1^{-}={(H_x-j{H}_y)}^{\ast }/2\end{array}$$ (3)

where H_x and H_y are the x and y oriented RF magnetic fields created by the coil. We use (2) to derive these transverse magnetic components, and MREPT utilizes these two measurements to reconstruct the EP values of biological tissues.

B. Dual-excitation algorithm – the inverse problem

Consider the magnetic permeability inside biological tissues to be equal to that in a vacuum. Ampere's Law reads

$$\nabla \times \mathbf{\text{H}}=\sigma \mathbf{\text{E}}+j\omega {\epsilon }_r{\epsilon }_0\mathbf{\text{E}}$$ (4)

Using the complex permittivity ε_c = ε_rε₀ − jσ/ω, we have

$$\nabla \times \mathbf{\text{H}}=j\omega {\epsilon }_c\mathbf{\text{E}}$$ (5)

Taking the curl of both sides of (5) and substituting with ∇ × E = − jωμ₀H, we get

$$-{\nabla }^2\mathbf{\text{H}}={\omega }^2{\mu }_0{\epsilon }_c·\mathbf{\text{H}}+j\omega (\nabla {\epsilon }_c)\times \mathbf{\text{E}}$$ (6)

or its matrix form

$$\left[\begin{array}{c}-{\nabla }^2{H}_x\\ -{\nabla }^2{H}_y\\ -{\nabla }^2{H}_z\end{array}\right]={\omega }^2{\mu }_0{\epsilon }_c\left[\begin{array}{c}{H}_x\\ H_y\\ H_z\end{array}\right]+j\omega \left[\begin{array}{ccc}0& E_z& -E_y\\ -E_z& 0& E_x\\ E_y& -E_x& 0\end{array}\right]\left[\begin{array}{c}\partial {\epsilon }_c/\partial x\\ \partial {\epsilon }_c/\partial y\\ \partial {\epsilon }_c/\partial z\end{array}\right]$$ (7)

According to Ampere's Law, we replace the electric field components with magnetic field components as follows

$$\{\begin{array}{c}{E}_x=(\partial H_z/\partial y-\partial H_y/\partial z)/j\omega {\epsilon }_c\\ E_y=(\partial H_x/\partial z-\partial H_z/\partial x)/j\omega {\epsilon }_c\\ E_z=(\partial H_y/\partial x-\partial H_x/\partial y)/j\omega {\epsilon }_c\end{array}$$ (8)

For regular birdcage coils, the axial z component of the end-ring generated magnetic field (H_z) is nonproductive for NMR excitation, and can become a source of ohmic loss to induced conduction currents in the tissue load conductor. To solve this problem, the TEM resonator was developed [34], in which the coil's return path follows the shield rather than the end rings, and a rung-current-generated transverse magnetic field without the counterproductive end-ring currents is achieved. In this case, we can neglect the H_z component in (8), and rewrite (7) as

$$\{\begin{array}{cc}-{\nabla }^2{H}_x& ={\omega }^2{\mu }_0{H}_x{\epsilon }_c-(\partial H_x/\partial z)[(\partial {\epsilon }_c/\partial z)/{\epsilon }_c]\\ & +(\partial H_y/\partial x-\partial H_x/\partial y)[(\partial {\epsilon }_c/\partial y)/{\epsilon }_c]\\ -{\nabla }^2{H}_y& ={\omega }^2{\mu }_0{H}_y{\epsilon }_c-(\partial H_y/\partial z)[(\partial {\epsilon }_c/\partial z)/{\epsilon }_c]\\ & +(\partial H_y/\partial x-\partial H_x/\partial y)[(\partial {\epsilon }_c/\partial x)/{\epsilon }_c]\end{array}$$ (9)

In (9), H_x and H_y distributions correspond to B₁-mapping results, while ε_c, (∂ε_c/∂x)/ε_c, (∂ε_c/∂y)/ε_c and (∂ε_c/∂z)/ε_c are unknown. Upon acquiring another set of H_x ∼ H_y data, we can form a set of linear equations with four equations and four unknown variables, and thus ε_c can be solved.

Two methods can be adopted to acquire two sets of H_x ∼ H_y data: (a) adjusting the RF coil excitation modes, such as linear (vertical and/or horizontal polarization) and/or quadrature modes [35], to excite the imaging object twice, separately, but with the same subject orientation; or (b) rotating the subject along the z-axis by an angle. In the present study, we used the linear excitation mode to generate two polarizations by switching the current feed points to positions 90 degrees apart from each other.

III. Materials and Methods

A. FEM Model of the Head and Coil

T1-weighted MRI images (128×128×72, 2×2×2mm³) of a human head, which covered the entire brain, were acquired from a 3T Siemens MRI system. The head images were then segmented into five tissues: scalp, skull, CSF, WM and GM. The structural information was imported into ANSYS software, and a five-tissue anatomically accurate head model was constructed using a hexahedral element with a mesh size of 2×2×2mm³, which is equivalent to the voxel size of MRI images.

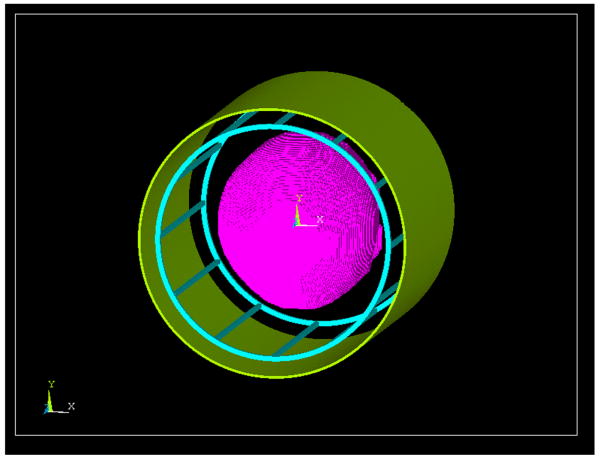
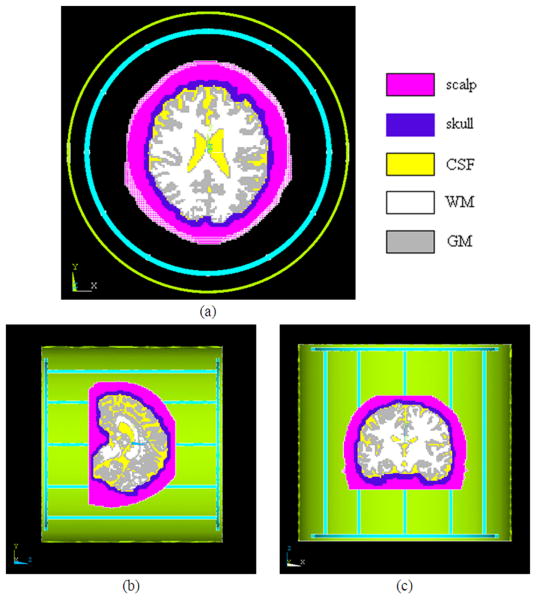
A 12-rung birdcage coil and a TEM coil with diameters of 28cm and lengths of 28cm were modeled. Either coil was enclosed by a cylindrical shield having a diameter of 32cm and a length of 30cm. Both the coils and the shield(s) were meshed with the tetrahedral element and assigned with copper material. Fig. 1 illustrates the FEM models of the head and shielded birdcage coil in ANSYS, and Fig. 2 shows the structural views on the axial, sagittal and coronal planes.

Fig. 1.

Overview of the head FEM model and a 12-rung shielded birdcage coil FEM model (green: copper shield, cyan: rungs and end-rings, magenta: head)

Fig. 2.

Axial (a), sagittal (b) and coronal (c) views of the FEM models. The head model was meshed with hexahedral element while the coil with tetrahedral element.

Since all RF coils are basically open structures, the field generated by a coil radiates into a large space. However, a numerical simulation can be performed only inside a finite space. Therefore, we must first truncate the simulation space by using an air volume to enclose the solution area. In order to reduce the artificial field reflection produced by the volume, we used a Perfectly Matched Layer (PML) [36] to surround the artificial surface of the air volume. For our shielded coils, the shield provided the truncation at which the boundary condition n̂ × E = 0 should be applied [35]. Both air and PML volumes were discretized with the tetrahedral element.

B. Coil Excitation

To perform a linear excitation, the equivalent circuit model [35] was utilized to calculate the electric current in each rung. All of the capacitors in the coil were replaced with current sources at the required resonant frequency. For the birdcage coil, the current $I_i^{\mathit{\text{rung}}}$ flowing in the ith rung is

$$I_i^{\mathit{\text{rung}}}=I_{0}sin[(i-0.5)\pi /6]$$ (10)

where I₀ denotes the maximum current. In our study, I₀ was assumed to be unit current, so the current flowing in the end-rings between the ith and (i+1)th rungs is

$$I_i^{\mathit{\text{end–ring}}}=\pm cos(i·\pi /6)/0.52$$ (11)

For the TEM coil, the current in each end-ring was assigned to be zero. Similar current configurations can also be found in [37].

π/2 and π/6 offset was added on the phase of the current flowing in the coil, separately, to simulate the current feed point switching. Three coil excitation schemes are listed in TABLE I.

Table I.

Specifications of Coil Excitation Schemes

	current in the ith rung	current feed point	generated magnetic field
Scheme 1 (S1)	$I_i^{\mathit{\text{rung}}}=I_{0}sin[(i‐0.5)\pi /6]$	--	$H_x^1$ and $H_y^1$
Scheme 2 (S2)	$I_i^{\mathit{\text{rung}}}=I_{0}sin[(i‐0.5)\pi /6+\pi /2]$	90° apart from that of scheme 1	$H_x^2$ and $H_y^2$
Scheme 3 (S3)	$I_i^{\mathit{\text{rung}}}=I_{0}sin[(i‐0.5)\pi /6+\pi /6]$	30° apart from that of scheme 1	$H_x^3$ and $H_y^3$

C. Simulation Protocols

Simulations were conducted in 3T (128MHz) environment. The corresponding target EP values for different head tissues were derived from the 4-Cole-Cole Model [4] and are listed in Table II.

Table II.

EP Values of Head Tissues

Human head	σ (S/m)	εr
Scalp	0.54	62
Skull	0.12	21
CSF	2.14	84
White Matter	0.34	52
Gray Matter	0.59	73

Using ANSYS software as the forward solver, we generated the simulated data of H_x and H_y by different coil excitation schemes, correspondingly. Simulations were conducted on both the birdcage coil and TEM coil to evaluate the influence of neglecting the H_z component in (9).

We define relative error (RE) and correlation coefficient (CC) of the reconstructed EPs images as

$$\begin{array}{l}{\text{RE}}_{{\sigma }_{\mathit{\text{tissue}}}}=\sqrt{\sum _{i=1}^N{({\sigma }_i^{\ast }-{\sigma }_{\mathit{\text{tissue}}})}^2/{\sigma }_{\mathit{\text{tissue}}}^2}\\ {\text{RE}}_{{\epsilon }_{\mathit{\text{tissue}}}}=\sqrt{\sum _{i=1}^N{({\epsilon }_i^{\ast }-{\epsilon }_{\mathit{\text{tissue}}})}^2/{\epsilon }_{\mathit{\text{tissue}}}^2}\\ {\text{CC}}_{{\sigma }_{\mathit{\text{tissue}}}}=\sum _{i=1}^N({\sigma }_i^{\ast }·{\sigma }_{\mathit{\text{tissue}}})/\sqrt{N{({\sigma }_{\mathit{\text{tissue}}})}^2·\sum _{i=1}^N{({\sigma }_i^{\ast })}^2}\\ {\text{CC}}_{{\epsilon }_{\mathit{\text{tissue}}}}=\sum _{i=1}^N({\epsilon }_i^{\ast }·{\epsilon }_{\mathit{\text{tissue}}})/\sqrt{N{({\epsilon }_{\mathit{\text{tissue}}})}^2·\sum _{i=1}^N{({\epsilon }_i^{\ast })}^2}\end{array}$$ (12)

where σ_tissue and ε_tissue are the target EP values, and ${\sigma }_i^{\ast }$ and ${\epsilon }_i^{\ast }$ are the estimated values in the ith pixels within the specified tissue.

In order to test the noise tolerance of the proposed algorithm, we added Gaussian white noise (GWN) to the simulated B₁ field data. From (3) we get the circularly-polarized components of the B₁ field, then add GWN to the amplitude and phase of ${\mathit{\text{H}}}_1^{+}$ and ${\mathit{\text{H}}}_1^{-}$, respectively. The noise level is evaluated by SNR_B1, which is defined as follows

$${\text{SNR}}_{\text{B}1}=A/s_{\mathit{\text{amp}}}$$ (13)

where A is the amplitude of the noise-free B₁ field voxel signal and s_amp is the standard deviation (STD) of amplitude noise. In the present study, we assumed SNR_B1=200, 150 and 100. Note that here, SNR_B1 is different from the commonly denoted SNR of MRI systems (SNR_MRI). A related description can be found in the Discussion and Appendix.

The Wiener adaptive lowpass-filter was applied to pre-process the “contaminated” B₁ maps, and (3) was re-used to derive the H_x and H_y components.

IV. Simulation Results

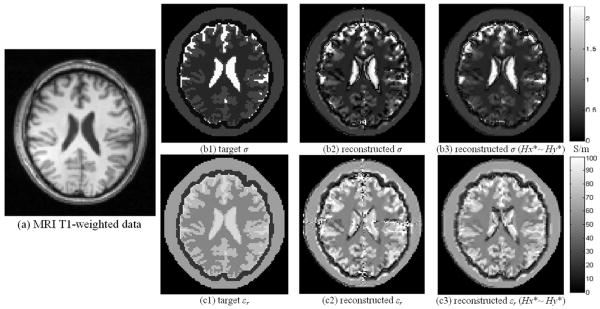
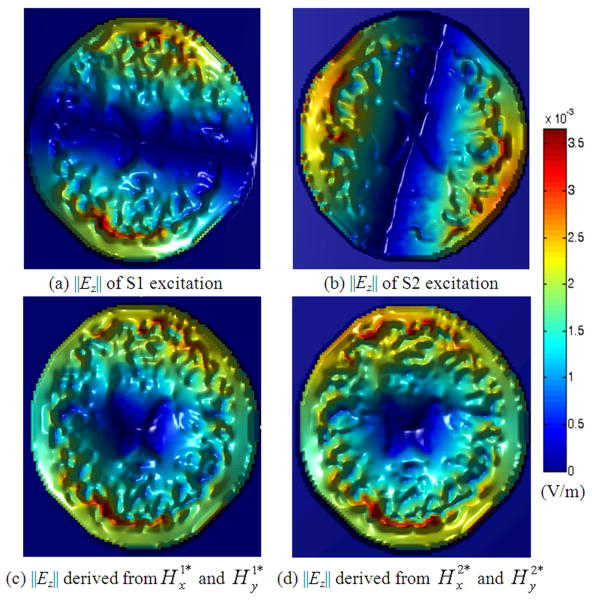
We chose the central slice (z=0) of the head model as the slice of interest, and the corresponding MRI T1-weighted image is depicted in Fig. 3 (a). Figs. 3 (b1) and (c1) draw the target EP distributions after image segmentation. Using the 28cm-long TEM coil, with $H_x^1\sim H_y^1$ and $H_x^1\sim H_y^2$ data acquired from coil excitation schemes S1 and S2, the reconstructed EP distributions are shown in (b2) and (c2). Two bright stripe-like artifacts along the x- and y-axes are observed in above results, and this phenomenon resulted from the characteristics of the E_z distribution inside the linearly polarized RF coil. Figs. 4 (a) and (b) depict the modulus of the E_z distribution on the central axial slice within the head using S1 and S2 excitations, in which the E_z modulus varied rapidly and dropped to zero in the area across the x-axis in (a) and the y-axis in (b). We define D_H = (∂H_y/∂x − ∂H_x/∂y), and D_H has the same modulus distribution with E_z according to (8). Since D_H acts as a denominator in our algorithm as (9) indicates, its “zero” area would introduce numerical errors, which are observed in the reconstruction results in Fig. 3 as two bright stripe-like artifacts.

Fig. 3.

MRI T1-weighted image (a) of the slice of interest, segmented target EP distributions (b1) &. (c1), reconstructed EP distributions (b2) &. (c2), and reconstructed EP distribution (b3) &. (c3) using H_x ∼ H_y data when noise free. Using the 28cm-long TEM coil, coil excitation schemes S1 and S2 were applied. Two bright stripe-like artifacts along x- and y-axes can be observed in (b2) and (c2).

Fig. 4.

‖E_z‖ distribution with the TEM coil when noise-free. Coil excitation schemes S1 and S2 were applied. (a) and (b) depict ‖E_z‖ distribution for each excitation scheme, and (c) and (d) show the ‖E_z‖ distribution corresponding to our newly produced B₁ field. Much lower intensity can be observed along x- and y-axes in (a) and (b), and in the central area in (c) and (d).

To solve the above problem, we produced two new sets of $H_x^{\ast }\sim H_y^{\ast }$ data by

$$\{\begin{array}{c}{H}_x^{1\ast }=(H_x^1+j{H}_x^2)/2\\ H_y^{1\ast }=(H_y^1+j{H}_y^2)/2\end{array}\text{and}\{\begin{array}{c}{H}_x^{2\ast }=(H_x^1-j{H}_x^2)/2\\ H_y^{2\ast }=(H_y^1-j{H}_y^2)/2\end{array}$$ (14)

In a linear medium, the system described by Maxwell's equations is a linear system; according to the superposition principle, $H_x^{\ast }$ and $H_y^{\ast }$ still hold for (9). Figs. 4 (c) and (d) show the ‖E_z‖ distribution corresponding to the new $H_x^{\ast }\sim H_y^{\ast }$ data, and Figs. 3 (b3) and (c3) show the reconstructed EP results using $H_x^{\ast }\sim H_y^{\ast }$ data when noise-free. The bright stripe-like artifacts disappear in the reconstructed images; however, there are still little artifacts in the reconstructed images, and they mainly resulted from much lower intensity of the ‖E_z‖ distribution in the central area, as Figs. 4 (c) and (d) depict, which is about 1/100 of the periphery intensity. Reconstruction results for CSF, WM and GM tissues are listed in TABLE III, and their relative errors range within 12% ∼ 28% while correlated coefficients all above 0.91. Similar $H_x^{\ast }\sim H_y^{\ast }$ data processing have been applied in the following simulations.

Table III.

Relative Errors and Correlation Coefficients of Reconstructed Electric Properties without and With H_Z Component Using Tem and Birdcage Coils

REs / CCs		28cm TEM without HZ		28cm BC without HZ		28cm BC with HZ		12cm BC without HZ
CSF	σ	27.1%	0.971	30.1%	0.899	28.2%	0.943	39.4%	0.8525
	εr	24.9%	0.936	26.3%	0.902	24.3%	0.920	38.1%	0.8908
WM	σ	21.4%	0.940	28.6%	0.898	25.1%	0.908	38.9%	0.8430
	εr	12.7%	0.982	15.3%	0.963	12.6%	0.987	28.6%	0.9258
GM	σ	28.6%	0.913	32.2%	0.888	27.7%	0.919	40.6%	0.8513
	εr	18.0%	0.969	18.8%	0.958	16.5%	0.974	39.1%	0.8585

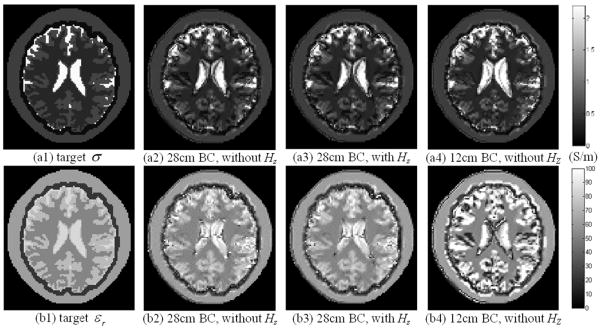
In our algorithm, ∂H_z/∂y and ∂H_z/∂x are assumed to be negligible. Since birdcage coils have been widely used in clinical applications, it is necessary to evaluate the H_Z effects for regular birdcage coils. We applied the dual-excitation algorithm on the 28cm-long birdcage, and we also took ∂H_z/∂y and ∂H_z/∂x into equation (9) to finish the reconstruction using the same coil. In addition, we constructed a 12cm-long birdcage coil (with the same other geometrical parameters and configurations as the 28cm-long birdcage coil) to evaluate its performance. Coil excitation schemes S1 and S2 were applied. Reconstructed EPs distribution and simulation results are shown and summarized in Fig. 5 and TABLE III, respectively. It can be observed that, when H_Z component was considered we could surely improve EPs reconstruction results. However, while the experimental measurement of H_Z component is not feasible in MRI, it is also reasonable to assume H_Z = 0 within a common birdcage coil which could also provide well-differentiated structural information of biological tissues.

Fig. 5.

Reconstructed electric property distribution within a 28cm-long and a 12cm-long birdcage coil. Upper row: conductivity, bottom row: relative permittivity. From left to right: target EP distribution, reconstruction results without and with H_Z component in the birdcage coils, respectively.

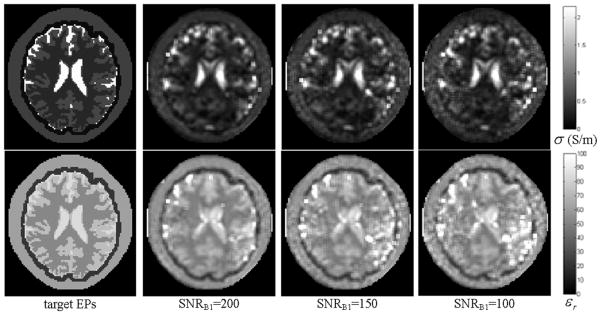
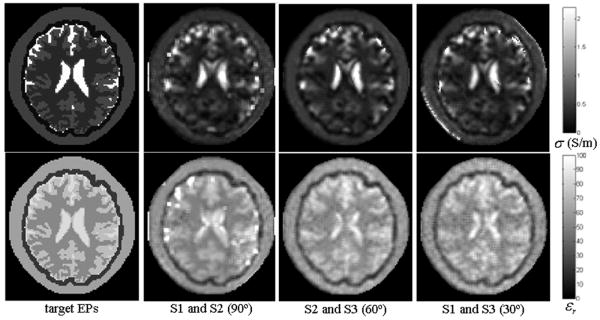
Fig. 6 shows the reconstructed EPs distribution when noise was added with SNR_B1=200, 150 and 100. The corresponding REs and CCs are summarized in TABLE IV. The 28cm-long TEM coil and S1 and S2 coil excitations were used. We also applied S2 and S3, S1 and S3 -- choosing two adjacent rungs as current feed points individually -- to excite the TEM coil with noise (SNR_B1=200). A comparison of the reconstruction results is depicted in Fig. 7. It can be observed that, when added with noise, all the tissues could be differentiated in the reconstruction results; and similar tissue patterns could also be produced while different coil excitation scheme combinations were utilized.

Fig. 6.

Reconstructed electric property distribution within a 28cm-long TEM coil. Upper row: conductivity, bottom row: relative permittivity. From left to right: target EP distribution, reconstruction results with decreasing SNR_B1.

Table IV.

Relative Errors and Correlation Coefficients of Reconstructed Electric Property Distribution with Decreasing SNR_B1.

REs / CCs		SNRB1=200		SNRB1=150		SNRB1=100
CSF	σ	46.4%	0.690	50.1%	0.679	67.1%	0.657
	εr	28.6%	0.751	34.4%	0.701	56.8%	0.659
WM	σ	39.1%	0.788	53.2%	0.749	74.4%	0.735
	εr	27.4%	0.901	33.8%	0.874	45.1%	0.821
GM	σ	49.1%	0.761	60.2%	0.732	74.1%	0.714
	εr	24.6%	0.861	40.9%	0.852	46.2%	0.811

Fig. 7.

Reconstructed electric property distribution with different coil excitation scheme combinations. Upper row: conductivity, bottom row: relative permittivity. From left to right: target EP distribution and reconstructed distribution with different phase offset of the current flowing in the coil.

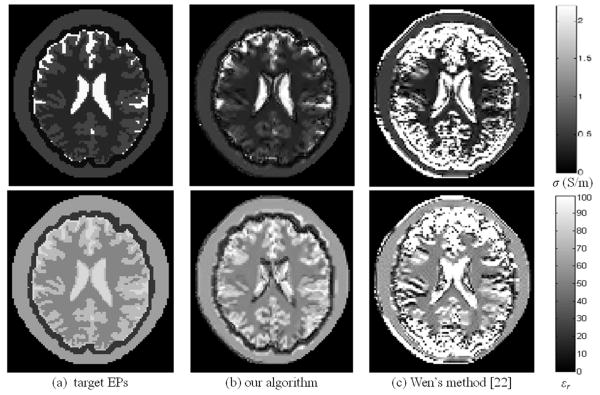
We also applied Wen's method in [22] to the TEM model by S1 and S2 excitations to reconstruct the EPs distribution. Fig. 8 shows the comparison of the reconstruction results when noise-free. It can be seen that we obtained better results around the tissue boundary regions, and this is because the term of jω(∇ε_c) × E of (6) was not taken into account in the modified Helmholtz equation in Wen's method.

Fig. 8.

Reconstructed electric property distribution with the TEM coil when noise-free, and coil excitation schemes S1 and S2 were applied (upper row: σ distribution, bottom row: ε_r distribution; from left to right: target EPs, using our algorithm, and using Wen's method [22]).

V. Discussion

Since the conductivity and permittivity values of tissues change with their physiological and pathological conditions, EP maps could provide useful diagnostic information. MREPT promises to reconstruct not only the conductivity distribution, as EIT, MIT, MREIT and MAT-MI aim to do, but also the permittivity distribution within biological tissues, thus enriching our observations of their conditions. In addition, as it is based on B₁-mapping, which has been developed and pursued for decades, MREPT does not require electrode mounting or external energy deposition, which pose potential safety concerns. It could provide a high spatial resolution in imaging EPs with the aid of MRI. In the present study, we have proposed a new dual-excitation MREPT algorithm, and as our simulation results indicate, the dual-excitation algorithm furnishes us with a practical approach to reconstructing the conductivity and permittivity distributions within a human head while avoiding the need to solve the ill-posed inverse problem present in traditional EIT. The desirable reconstruction results of tissues with heavier implications in physiology and pathology (such as CSF, WM and GM) suggest that MREPT imaging deserves further investigation, can be extended to other organs of the human body, and may have wide clinical applications.

In our algorithm, the z component of the magnetic field intensity H_z is neglected. Our simulation results suggest that the dual-excitation algorithm still works well, even using a typical birdcage coils (Fig. 5) in which the H_z component prominently exists and is mainly generated by end-rings. Using a TEM coil, we can get better reconstruction EP images with higher accuracy.

To eliminate the bright stripe-like artifacts in Fig. 2, we produced two new sets of $H_x^{\ast }\sim H_y^{\ast }$ according to the superposition principle. Alternatively, to generate a similar ‖E_z‖ distribution as in Figs. 3 (c) and (d), we may also excite the coil by quadrature polarization which is commonly utilized in commercial RF coils. However, since our algorithm needs to excite the coil twice, at least three current feed points will be required to perform the quadrature excitation twice. Therefore, our approach of using data acquired from two linear excitations appears to be more feasible and easy to implement.

In contrast to the previously proposed MREPT algorithms in [21] and [23], our approach does not require iterative computation which needs precise coil and subject modeling and is time consuming. Compared with the method in [22], ours is more capable to deal with regions where the EPs distribute inhomogeneously and discontinuously. Fig. 8 illustrates this point.

Uniqueness of solution is an important issue in inverse problems. We applied three coil excitation schemes, and conducted the reconstruction procedures by choosing two 30°-apart (adjacent), 60°-apart and 90°-apart current feed points. It is shown in Fig. 7 that, under either excitation combination with noise added, our algorithm works well and produces overall similar distributions of the EPs. While these results suggest robustness and potential uniqueness characteristic of our algorithm, it is also indicated that when the switching current feed point is infeasible, our algorithm is still effective by careful subject rotation over a small angle inside the coil. In the future, the theoretical study on the uniqueness of the MREPT problem remains to be further performed.

In previous B₁ field simulation studies, the EP values were preset according to experimentally measured data [39] or the published 4-Cole-Cole dispersion relation [3]. However, in many instances, these two data are not in good agreement. Our algorithm will provide another effective way to accurately predict the EP values of biological tissues, and will also substantially benefit future studies in the MRI domain as well as other areas that involve EP configuration in the range of radio frequency.

For isotropic biological tissues, the SAR is defined by

$$\text{SAR}=\sigma (E_x^2+E_y^2+E_z^2)/2\rho$$ (15)

where ρ is the tissue density and is determined through experimental measurement. Once we get the B₁ distribution, the EP values can be obtained from the dual-excitation algorithm. Since H_x and H_y are more dominant in a birdcage and TEM coil, the electric field can be determined by Ampere's Law without H_z component, and we can directly calculate the SAR distribution. Thus, the evaluation of heat effects becomes more convenient.

In our algorithm, the Laplacian operation ∇²H amplifies noise effect. Thus the present algorithm is relatively sensitive to noise, as shown in Table IV when SNR drops. We have applied Wiener filtering over B₁ images; in addition, other feasible ways can be used to reduce noise level in experiment, such as taking multi-MRI scans in experiments and average B₁ images. Furthermore, for common B₁ mapping techniques, the scanning parameters are usually chosen as TR ≫ T1 ≫ TE, and the MRI image signal intensity depends on $\Vert {\mathit{\text{H}}}_1^{+}\Vert$ and $\Vert {\mathit{\text{H}}}_1^{-}\Vert$ via [21, 23, 38]

$$\text{SI}\propto M_0·sin(\gamma \Vert {\mathit{\text{H}}}_1^{+}\Vert \tau )\Vert {\mathit{\text{H}}}_1^{-}\Vert$$ (16)

where M₀ is the equilibrium magnetization, γ the gyromagnetic ratio of ¹H, and τ the duration of rectangular RF pulse. For small flip angle pulse, (16) can be written as

$$\text{SI}\propto \gamma ·\tau ·M_0(\Vert {\mathit{\text{H}}}_1^{+}\Vert ·\Vert {\mathit{\text{H}}}_1^{-}\Vert )$$ (17)

and image signal intensity is propositional to $\Vert {\mathit{\text{H}}}_1^{+}\Vert ·\Vert {\mathit{\text{H}}}_1^{-}\Vert$. When we add noise into $\Vert {\mathit{\text{H}}}_1^{+}\Vert$ and $\Vert {\mathit{\text{H}}}_1^{-}\Vert$ leveled by SNR_B1, it can be proved that the corresponding SNR_MRI will be lower than SNR_B1 (see Appendix); in other words, SNR_B1 is $\sqrt{2}$ times higher than SNR_MRI. Moreover, note that we only consider noise in the B₁ field in such a case; since there are other noise sources in the MRI signal detection process, such as thermal fluctuation and electronics factors, SNR_B1 is even higher than SNR_MRI. Therefore, our assumption that SNR_B1 equals to 100 ∼ 200 is reasonable for regular MRI scanning.

A multi-port quadrature coil can be driven at each one point by well-controlled RF drive circuit [34], thus it is applicable to acquire different B₁ data to finish the reconstruction. Besides, our algorithm requires B₁ field measurements. Until now, many B₁-mapping techniques have been proposed, and the measurement of B₁ field intensity has been well established, while phase measurement has been studied by few groups [22, 23, 40]. Recently, a novel B₁ phase mapping method was developed in local B₁ shimming studies for transceiver arrays [41], and it provides us with the possibility for accurate B₁ phase mapping. In the future, more efforts should be focused on the pursuit of B₁ complex image mapping in order to improve the efficiency and accuracy of the MREPT technique.

Appendix: Derivation of SNR_MRI From SNR_B1

Noise in B1 field is leveled by SNR_B1 in (13) via

$${\text{SNR}}_{\text{B}1}=\{\begin{array}{c}\Vert H_1^{+}\Vert /s_1\\ \Vert H_1^{‐}\Vert /s_2\end{array}$$ (18)

where $\Vert {\mathit{\text{H}}}_1^{+}\Vert$ and $\Vert {\mathit{\text{H}}}_1^{‐}\Vert$ are noise-free voxel intensity, and s₁ and s₂ are the STD of two uncorrelated GWN added into $\Vert {\mathit{\text{H}}}_1^{+}\Vert$ and $\Vert {\mathit{\text{H}}}_1^{‐}\Vert$, respectively. We use n₁ and n₂ to represent these two noise values. Then we have

$$(\Vert H_1^{+}\Vert +n_1)·(\Vert H_1^{‐}\Vert +n_2)=\Vert H_1^{+}\Vert ·\Vert H_1^{‐}\Vert +\Vert H_1^{+}\Vert ·n_2+\Vert H_1^{‐}\Vert ·n_1+n_1·n_2$$ (19)

with the variance as

$$\begin{array}{l}var(\Vert H_1^{+}\Vert ·\Vert H_1^{‐}\Vert +\Vert H_1^{+}\Vert ·n_2+\Vert H_1^{‐}\Vert ·n_1+n_1·n_2)\\ ={\Vert H_1^{+}\Vert }^2·var(n_2)+{\Vert H_1^{‐}\Vert }^2·var(n_1)+var(n_1)·var(n_2)\\ =s_2^2·{\Vert H_1^{+}\Vert }^2+s_1^2·{\Vert H_1^{‐}\Vert }^2+s_1^2·s_2^2\\ ={\Vert H_1^{+}\Vert }^2·{\Vert H_1^{‐}\Vert }^2(1/{\text{SNR}}_{\text{B}1}^2+1/{\text{SNR}}_{\text{B}1}^2+1/{\text{SNR}}_{\text{B}1}^4)\\ \approx 2{\Vert H_1^{+}\Vert }^2·{\Vert H_1^{‐}\Vert }^2/{\text{SNR}}_{\text{B}1}^2\end{array}$$ (20)

and the corresponding SNR_MRI can be derived from (17) and (20) by

$$\begin{array}{ll}{\text{SNR}}_{\text{MRI}}\hfill & =\text{SI}/\text{STD}(\text{SI})\\ & =(\Vert H_1^{+}\Vert ·\Vert H_1^{‐}\Vert )/(\sqrt{2}\Vert H_1^{+}\Vert ·\Vert H_1^{‐}\Vert /{\text{SNR}}_{\text{B}1})\\ & ={\text{SNR}}_{\text{B}1}/\sqrt{2}\end{array}$$ (21)