The Charge-Transfer Properties of the S₂ State of Fucoxanthin in Solution and in Fucoxanthin Chlorophyll-a/c₂ Protein (FCP) Based on Stark Spectroscopy and Molecular-Orbital Theory

Abstract

The membrane-intrinsic light harvesting complex from the diatom Cyclotella meneghiniana, fucoxanthin chlorophyll-a/c₂ protein (FCP), is characterized by Stark spectroscopy to obtain a quantitative measure of the excited-state dipolar properties of the constituent pigments. The electro-optical properties of the carotenoid fucoxanthin (Fx), the primary light harvester in FCP, were determined from the Stark spectrum measured in a MeTHF glass (77 K) and compared to the results from electronic-structure calculations. On photon absorption by Fx, a 17 D change in the static dipole moment (|Δμ⃗|_exp), and a somewhat larger |Δμ⃗|_exp at the red edge, are measured for the S₀ → S₂ $(1^1{\mathrm{A}}_{\mathrm{g}}^{-}-\text{like}\to 1^1{\mathrm{B}}_{\mathrm{u}}^{*+}-\text{like})$ transition. The significant change in dipolar properties demonstrates that Fx undergoes photoinduced charge transfer (CT), and underscores the influence of the S₂ state on the polarity-dependent excited-state dynamics of Fx that has so far been attributed to, and discussed in terms of, the S₀ and the S₁/ICT states. MNDO-PSDCI and SACCI-CISD calculations indicate that the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state intrinsically possesses a dipole moment much smaller than the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state, suggesting that solvent fields promote the mixing of these two states and accounts for the large dipole moments measured here for the S₀ → S₂ transition. These CT properties of the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state of Fx, which are further enhanced in the protein, underpin its photosynthetic capabilities for light harvesting and energy transfer (ET). In FCP, the CT properties of the Fx’s vary according to the energetic position: between 450 and 500 nm there appear to be two sets of Fx’s that exhibit |Δμ⃗|_exp values on the order of 5 and 15 D, whereas the red-most Fx’s, that are very efficient in ET to chlorophyll-a (Chl-a), exhibit strikingly large |Δμ⃗|_exp values on the order of 40 D. Such magnitudes of |ΔΔμ⃗|_exp suggest a mechanism to enhance Coulombic coupling to promote ET from the S₂ state of Fx to Chl-a. These three sets of Fx’s, including a fourth red Fx, are identified by modeling the Stark spectrum of FCP using the Stark spectrum of Fx in MeTHF. In contrast to the Fx’s in the protein, the electrostatic properties of the Chl’s in FCP are comparatively much smaller. For the Q_y band of Chl-a, a |Δμ⃗|_exp of 0.92 D and a change in polarizability $({\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}})$ of 20 ų, indicate that the Chl-a’s are monomeric in nature and decoupled from each other.

Introduction

Diatoms are heterokontic algae responsible for about 25% of the primary biomass production on earth.¹ In both brown algae and diatoms, the latter which are unicellular eukaryotes, the membrane-bound light-harvesting complex (LHC), fucoxanthin chlorophyll-a/c protein (FCP), performs the primary step of absorbing and transferring solar energy in the photosynthetic cycle. The high degree of shared homology, and the common light-harvesting function between FCP and the LHC’s of higher plant thylakoid systems (LHCII),² has often led to cross referencing to LHCII, about which much is known, including its crystal structure,³ to better understand the properties of the pigments in FCP. In FCP, two of the three trans-membrane α-helices, and presumably the pigment binding sites therein, are the same as in LHCII.² Pigment compositions however differ, which limits the use of LHCII as a structural template to surmise the origin of the spectroscopic properties of the individual pigments in FCP. In particular, carotenoids are used in lieu of chlorophylls as the primary light harvesters in FCP, reflecting the adaptation of diatoms, and other organisms such as dinoflagellates, to survive in their marine environment.⁴ Thus, independent characterization of the photophysical properties of the carotenoid in FCP, that is, fucoxanthin (Fx), is important to understand the process and mechanism behind the first step of photosynthesis in diatoms and brown algae.

The role conferred on carotenoids in marine organisms, including Fx in diatoms and peridinin in dinoflagellates, is not only promoted by their increased content relative to the chlorophylls, but also by a structural modification to include a carbonyl moiety in conjugation with the polyene backbone (Scheme 1 in Supporting Information). This results in extending their light-absorbing capability into the blue-green range (λ_max ≈ 500 nm) required for successful photosynthesis in the oceans, and moreover makes the carotenoids efficient channels for transferring this absorbed energy to chlorophyll-a (Chl-a). This functionality of carotenoids may be better understood from the description of their spectral properties, by reference to the C_2h point group of linear polyenes, where the strongly allowed π−π* transition is not to the lowest-energy singlet S₁ state (2¹Ag), which is symmetry forbidden and not accessible by one-photon absorption from the ground state, but to a higher state, that is, S₀ → S_n (often n = 2), a 1¹A_g⃗ 1¹Bu-type transition. Note however that carotenoids, and in particular carbonyl-containing carotenoids such as Fx, are polar and asymmetric, and the description of their excited-state potential energy surface (PES) using the higher symmetry C_2h point group is an approximation. The corresponding labels for the ground- and first two excited-states are $1^1{\mathrm{A}}_{\mathrm{g}}^{-},2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like and $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like, respectively. The spectroscopic character of the excited states are influenced more by the configurational properties, denoted by their “ionic” (+) and ”covalent” (−) labels, than by their symmetric (g) versus unsymmetric (u) descriptions.^5,6

Besides the importance of Fx in the light-harvesting and energy-transfer function of FCP,^6–8 much interest in its intrinsic electronic properties has followed closely on the heels of peridinin, which has been extensively studied both in solution⁹ and in the water-soluble peridinin chlorophyll-a protein (PCP).^10–12 The similarity between Fx and peridinin is also mirrored in the carotenoid siphonaxanthin, found in green alga.¹³ Of particular interest, and relevance, is the presence of a ubiquitous intramolecular charge-transfer (ICT) state,¹⁴ that sets these carbonyl-containing carotenoids apart from others.^7,15 This ICT state, which is strongly coupled to the S₁ state and more generally referred to as the S₁/ICT state,¹⁶ functions with more than 90% efficiency to transfer energy to Chl-a in PCP.¹¹ Transient absorption (TA) studies on the membrane-intrinsic LHC’s of both dinoflagellates¹⁷ and diatoms, that is, FCP,⁸ have also demonstrated the presence and necessity of the so-called S₁/ICT state to carry out ET to Chl-a. The functional importance of this ICT state motivated a Stark-effect study on peridinin¹⁸ from which the changes in static dipole moment (|Δμ⃗|_exp) and polarizability $({\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\mathit{\text{exp}}})$, on absorption, were obtained. In the case of peridinin, it was presumed that even a very weakly absorbing ICT state would produce a large Stark signal. Instead the S₂ state itself was found to possess significant CT character. Given that Fx is structurally similar to peridinin, and its polarity sensitive excited-state dynamics have also been attributed to an ICT state,¹⁴ the current Stark-effect study aims to uncover whether the electronic properties of the S₂ state in Fx may also be implicated in its excited-state reactivity.¹⁸ The nature and origin of the CT properties of the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state are examined in greater detail for Fx with the help of electronic-structure calculations including MNDO-PSDCI, SACCI-CISD, and TD-DFT methods. The current Stark-effect study in conjunction with electronic-structure calculations on Fx provides a detailed characterization of the electronic properties of this carotenoid outside the protein environment, to ultimately understand how it functions within the protein.

The FCP complex studied here is isolated from the centric diatom Cyclotella meneghiniana.^19,20 It is composed of oligomers (FCPb complexes) built of 2–3 units of trimers exclusively consisting of 19 kDa subunits (fcp5), in addition to independent trimeric FCPa complexes that are mostly composed of 18 kDa polypeptides (fcp1–3) and some 19 kDa peptides (fcp6/7).¹⁹ These differences do not affect the steady-state absorption and fluorescence spectra, which are very similar for the oligomers and trimers, and only the CD signals differ.¹⁹ The evaluation of the electrostatic properties from the Stark spectra of FCP, and of isolated Fx, is expected to lead to a better understanding of the mechanism that controls pigment functionality in FCP. The dipolar properties that are evaluated from Stark spectra²¹ can also be used to probe intermolecular interactions that are affected by the electronic interactions in the binding site and the proximity of pigments in the protein complex.

In addition to Fx, chlorophylls comprise more than half the pigments in FCP and serve to harvest solar energy and subsequently transfer the energy from the light-harvesting complex to the reaction center. FCP also differs from LHCII in its chlorophyll composition: chlorophyll-c₂ (Chl-c₂) replaces chlorophyll-b (Chl-b) thereby increasing the ability of FCP to capture light more efficiently in the Soret region due to the higher extinction coefficient of Chl-c₂. Although not the focus of the current study, the electronic properties of Chl-a and Chl-c₂ are also measured and used to understand how the pigments interact electrostatically. In addition to Fx in FCP, there are trace amounts of the carotenoid diadinoxanthin (Ddx), which not only functions as a precursor to the formation of Fx, but is also implicated in the xanthophyll cycle in diatoms and dinoflagellates.²² The de-epoxidation of Ddx to form diatoxanthin (Dtx) correlates to the conversion of violaxanthin to zeaxanthin in higher plants and the “nonphotochemical” quenching (npq) process that protects the organism from the effects of excess light absorption. However, the Ddx content, and more so Dtx, is too low in the FCP preparations studied here, and its electrostatic properties therefore cannot be accurately determined.

Materials and Methods

FCP and Fucoxanthin (Fx) Extraction

FCPs were isolated from the diatom Cyclotella meneghiniana, as described earlier.¹⁹ In brief, isolated thylakoid membranes were solubilized at 0.125 mg Chl-a/ml with 10 mM β-1,4-dodecyl maltoside (DDM) for 20 min on ice. They were then loaded on top of a continuous sucrose gradient achieved by a freeze-thaw cycle of a solution of 19% (w/v) sucrose in 10 mM Mes, pH 6.5, 2 mM KCl (buffer 1). Separation was carried out by centrifugation using a swing-out rotor at 200000g for 16 h, which was shown to be sufficient to reach equilibrium. Two bands of brown color were obtained in the upper part of the gradient. The lower band was harvested and concentrated using Amicon filtration devices with a cutoff of 30 kDa, and stored at −20 °C until use. The samples contained mostly FCPb higher oligomers accompanied by some FCPa trimers as proven by gel filtration.¹⁹ This was confirmed by SDS-PAGE, demonstrating the presence of mainly the 19 kDa subunit and some 18 kDa subunits. Steady-state absorption and fluorescence spectra were obtained at room temperature to verify the functional intactness of the FCPs.

Fx was isolated from the same organism as FCP. To this end cells were broken in 25 mM Tris, 1 mM dithiothreitol, pH 7.5, and spun at 70000g for 1 h. The resulting pellet was resuspended in 100% of ice-cold acetone and shortly spun, and the supernatant was collected. The pellet was extracted again with acetone, and the combined supernatants were dried using Sephadex G25 material. The crude pigment extract was dried in a rotary evaporator and redissolved in a small volume of acetone. Fx was separated by HPLC using a preparative column of the same specifications as described in ref 19. Eluted fucoxanthin from several runs was collected, the solvent was evaporated, and the samples were stored dry in the dark until use. To check for purity, analytical HPLC was carried out,¹⁹ which showed that over 99% of the Fx was in all-trans configuration. Fx concentration was determined in 100% acetone at 448 nm (∊ = 166 L/g cm).²³

Analyzing Stark (Electroabsorption) Spectra

The change in the absorption in response to an external electric field is precisely known as electroabsorption, but “Stark effect” is the terminology that has been widely used for such experiments on photosynthetic pigments and proteins and will be used here for practical purposes. The Stark effect on the absorption spectrum, A(ν̃), of an ensemble of molecules, is determined from the change in the intensity of the light, normalized by the total light intensity, transmitted through the sample in the presence of an external field where the change in absorbance (ΔA(ν̃)), averaged over all orientations, is²¹

$$\begin{array}{l}-\mathrm{\Delta }A(\tilde{v})={\overrightarrow{F}}_{\text{eff}}^2[a_{\chi }A(\tilde{v})+\frac{b_{\chi }\tilde{v}}{15h}\left\{\frac{\partial }{\partial \tilde{v}}\left(\frac{A(\tilde{v})}{\tilde{v}}\right)\right\}+\hfill \\ \hfill \frac{c_{\chi }\tilde{v}}{30h^2}\left\{\frac{{\partial }^2}{\partial {\tilde{v}}^2}\left(\frac{A(\tilde{v})}{\tilde{v}}\right)\right\}]\end{array}$$ (1)

The change in the absorbance, a function of energy (ν̃), is proportional to the square of the effective field (F⃗_eff) at the site of the solute, and to the weighted sum of the (field-free) absorption line shape A(ν̃) and first and second derivative functions of A(ν̃). The effective field, F⃗_eff = f_c × F⃗_ext, arises from the enhancement of the external field due to the polarization of the solvent, where f_c is the cavity-field factor,²¹ and F⃗_ext is the external applied field. When the angle between the applied AC electric-field vector and the electric-field vector of the polarized light, χ, is set at 54.7° (magic angle), the coefficients of the derivatives of A(ν̃) are related to the electrostatic properties of interest:

$$a_{54.7}=\frac{1}{30|\overrightarrow{m}{|}^2}{\displaystyle \sum _{\mathit{\text{ij}}}[10A_{\mathit{\text{ij}}}^2]+\frac{1}{15|\overrightarrow{m}{|}^2}{\displaystyle \sum _{\mathit{\text{ij}}}[10B_{\mathit{\text{ijj}}}]}}$$ (2)

$$b_{54.7}=\frac{1}{|\overrightarrow{m}{|}^2}{\displaystyle \sum _{\mathit{\text{ij}}}[10m_i{A}_{\mathit{\text{ij}}}\mathrm{\Delta }{\mu }_j]+\frac{15}{2}\overline{\mathrm{\Delta }{\alpha }_{\text{el}}}}$$ (3)

$$c_{54.7}=5|\mathrm{\Delta }\mu {|}^2$$ (4)

These equations do not include the temperature-dependent β term, which reduces to zero if the molecules remain randomly oriented in the presence of the external field,^21,24 which is found to be the case in rigid glassy matrices,²⁵ but may not necessarily apply in the protein environment. The coefficient a_54.7 (eq 1), usually very small compared to b_54.7 and c_54.7, is related to the electric-field induced change in the transition moment, m⃗: m⃗(F⃗_eff) = m⃗ + A•F⃗_eff + F⃗_eff•B • F⃗_eff, where A and B are the transition-polarizability and hyperpolarizability tensors, respectively. The first-derivative coefficient, b_54.7, is related to the second-rank tensor ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{el}}$, which in eq 3 is expressed as the average change in electronic polarizability between the ground and excited states. The scalar quantity ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{el}}=1/3\mathit{\text{Tr}}{(\overline{\mathrm{\Delta }\mathrm{\alpha }})}_{\text{el}})$. The experimental electro-optical parameter extracted from b_54.7 may however differ from ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{el}}$ if the extracted parameter contains non-negligible contributions from the cross term comprising the tensor element of A.^18,26 The latter term is often neglected to be able to obtain ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{el}}$ directly from b_54.7, and the shortcomings of this assumption have been clearly explained in other publications^25,27–29 and is particularly relevant if |Δμ⃗| is large.³⁰ The experimental parameter extracted from our fits is therefore denoted as ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$, to distinguish it from the pure electronic polarizability:

$${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}=\mathrm{\Delta }{\mathrm{\alpha }}_{\text{el}}+\frac{2}{15|\overrightarrow{m}{|}^2}{\displaystyle \sum _{\mathit{\text{ij}}}[10m_i{A}_{\mathit{\text{ij}}}\mathrm{\Delta }{\mu }_j]}$$ (5)

In contrast to ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$, the magnitude of the change in the static dipole moment, |Δμ⃗|, can be unambiguously determined from the square root of the coefficient of the second derivative at χ = 54.7° (eq 4). However, only the magnitude, and not the sign, of Δμ can be determined from the Stark signal, because the Liptay analysis assumes the molecules in the sample to be “frozen” in an isotropic orientation, both in the presence and absence of the external field.^21,24 Additional measurements with χ = 90° may yield the values for |m̂ • Δμ⃗|, from which the angle between |Δμ⃗| and the transition dipole moment, m̂, may be obtained. The coefficients of the derivatives, a_χ, b_χ, and c_χ, are extracted by means of a linear least-squares (LLSQ) fit of the electro-absorption signal to the sum of A(ν̃), and the first and second derivatives ofA(ν̃). The values of ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$ and |Δμ⃗|_exp, reported in Table 1 and Table 2, are the average of at least three independent measurements, and the error bars should be understood to reflect the precision of the experimental results obtained using the Liptay spectral analysis, which has been extensively applied to photosynthetic systems by Boxer and co-workers, ²⁸ among others.^31,32 Other analytical methods may however offer a different interpretation of the molecular parameters, which would affect their accuracy beyond that suggested by the error bars in Table 1 and Table 2.³⁰ The subscript “exp” indicates that these parameters include an enhancement due to the cavity-field factor, f_c. Therefore, the values of ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$ and |Δμ⃗|_exp should be divided by f_c ² and f_c, respectively, and their corresponding units expressed as ų/f_c ² and Debye/f_c, although f_c is omitted for clarity in the text. The cavity field factor, f_c, may be estimated from, ε₀ = ε₀(ε₀ − A_i(ε₀ − 1)),³³ where the shape factor A is defined in terms of the semiaxis, i, of the ellipsoidal cavity, in which fucoxanthin may be accommodated. Here, with semiaxes lengths of a_x = 15 Å and a_y = a_z = 5 Å, obtained from the MNDOCI calculations for Fx, a 10% augmentation of the electrostatic parameters is expected due to f_c. (Using molecular dimensions of a_x = 16.5 Å and a_y = a_z = 3.5 Å, obtained by roughly picking the end-to-end distances on the optimized Fx structure, the enhancement due to f_c is expected to be only 5%.)

TABLE 1.

Electronic Properties of Fucoxanthin (Fx) in MeTHF at 77 K

	fitFx-1a	fitFx-2B blue banda	red band
ν̃max (λmax) 298 Kb	22145 (451.5)
ν̃max (λmax) 7 Kb	21345 (468.5)	21345 (468.5)	19761 (506.0)
|Δμ⃗|exp (D)c	17.0 ± 0.08	15.4 ± 0.8	21.9 ± 0.8
|m̂ ·Δμ⃗|/| μ⃗|c	0.92 ± 0.07	0.90 ± 0.07	0.91 ± 0.09
${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$ (Å3)c	−680 ± 60	−1000 ± 100	−790 ± 40

^aFit_Fx-1 is the fit of the Stark spectrum to the absorption band (Figure 2b), and fit_Fx-2B is the fit to the red (sum of gaussians 1 and “g2a”) and blue (the sum of gaussians “g2b” to 5) bands shown in Figure 2c.

^bThe absorption maxima, ν˜_max, are reported in wavenumbers (cm⁻¹) and in nanometers (λ_max) in parentheses

^cThe experimental values of |μ⃗|_exp and |m̂ ·Δμ⃗|/|Δμ⃗| correspond to the difference dipole moment and the angle between |Δμ⃗| and the unit vector in the direction of the transition moment, m̂, respectively, between the ground (S₀) and excited (S₂) states. The latter value is ~20°. The $({\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}})$ value is an experimentally derived parameter that includes a transition-moment polarizability component. The electrostatic properties are enhanced by the cavity field factor: |Δμ⃗|_exp to f_c, and $({\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}})$ to f_c² (see Materials and Methods).

TABLE 2.

Electronic Properties of FCP in Glycerol/Buffer Glass at 77 K

	I A/B (Fx)	II A/B (Fx)		III (Fx)		IV (Chl Soret)
	fit-FCPA/B	fit-FCPA	fit-FCPB	fit-FCPA	fit-FCPB	fit-FCPA	Fit-FCPB
ν̃max a77 K	18320	19250		21460	20300	22883
(λmax)	(546)	(519)		(466)	(493)	(437)
|Δμ⃗|exp b(D)	37–45	4–7	10–14	4–6	15–18	4–6	2–4
${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$ b(Å3)	−1500 ± 500	450 ± 150	−1400 ± 600	−250 ± 50	850 ± 150	135 ± 35	30 ± 10

^aAbsorption maxima, ν̃_max, reported in wavenumbers (cm⁻¹) and in nanometers (λ_max) in parentheses, are the maxima of bands I, II, and III (situated in Fx absorbing regions) from fits-FCP_A and -FCP_B (see Results), except for IV which is the maximum of the absorption band in the Soret region.

^bThe experimental values of |Δμ⃗|_exp and ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$ for FCP, obtained in a glycerol/buffer glass at 77 K, are the same as described in the footnote, and include an enhancement due to f_c, and f_c ², respectively (see Materials and Methods).

Note that the dipolar properties have to be interpreted within the imprecision inherent in (a) analyzing overlapping absorption bands,^24,30 and (b) a slight orientation (a few degrees) of the pigments occurring in the presence of the external electric field,^25,27,34 which is often the case in multichromophore systems. Thus the dipolar values obtained for chromophores in the protein matrices should be considered as estimates unless their absorption bands are clearly resolved.

Sample and Instrumentation

Fucoxanthin was dissolved in MeTHF (Aldrich) at room temperature and inserted into a sample cell as described in ref 18. MeTHF was refluxed for 1–2 h and redistilled. The sample was not exposed to ambient light and was prepared quickly to minimize exposure to air. The protein samples were dissolved in nearly equal parts (v/v) of buffer 1 and 0.03% DDM to glycerol to yield ODs between 0.2 and 0.3 for the Soret band. Kapton tape (≈55 µm) and double-sided sticky tape (≈95 µm) were used as path length spacers for MeTHF and glycerol/buffer solutions, respectively. The external angle between the sample and the light beam is set at ~45°, for the magic angle measurements, by taking into account the refractive indices of liquid nitrogen (LN2) and of MeTHF (n = 1.79) at 77 K.³⁵

Electronic Structure Calculations

The electronic properties of the fucoxanthin chromophore were studied by using MNDO-PSDCI,^36–40 SAC-CI^41,42 and TD-DFT^43–45 molecular orbital theory. All calculations were based on a ground-state B3LYP/6-31G(d) minimized geometry.⁴⁶ The MNDO-PSDCI calculations included the eight highest energy occupied π orbitals, the three highest energy occupied σ orbitals, the eight lowest energy unoccupied π orbitals and the lowest energy unoccupied σ orbital. Full single and double CI was carried out within the π system and full single CI within the σ system. In some calculations, quadruple configurations involving the π orbitals were introduced by using a coupled cluster perturbative approximation. The one photon spectra and the output from the molecular orbital calculations were analyzed by using MathScriptor, which also generated Figure 5 and Figure 6. The MNDO-PSDCI and MathScriptor programs are available by contacting RR Birge (rbirge@uconn.edu). The TD-DFT calculations used various functionals ranging from low-correlation PBE1PBE to the high correlation SVWN (or LSDA) functionals.^44,45 The SAC-CI calculations were carried out using the D95 basis set and included energy-selected single and double CI with the highest energy unoccupied and the lowest energy unoccupied orbitals.^41,42 The ground-state minimizations, SAC-CI and TD-DFT calculations were carried out within the Gaussian 03 program.⁴⁶

Figure 5.

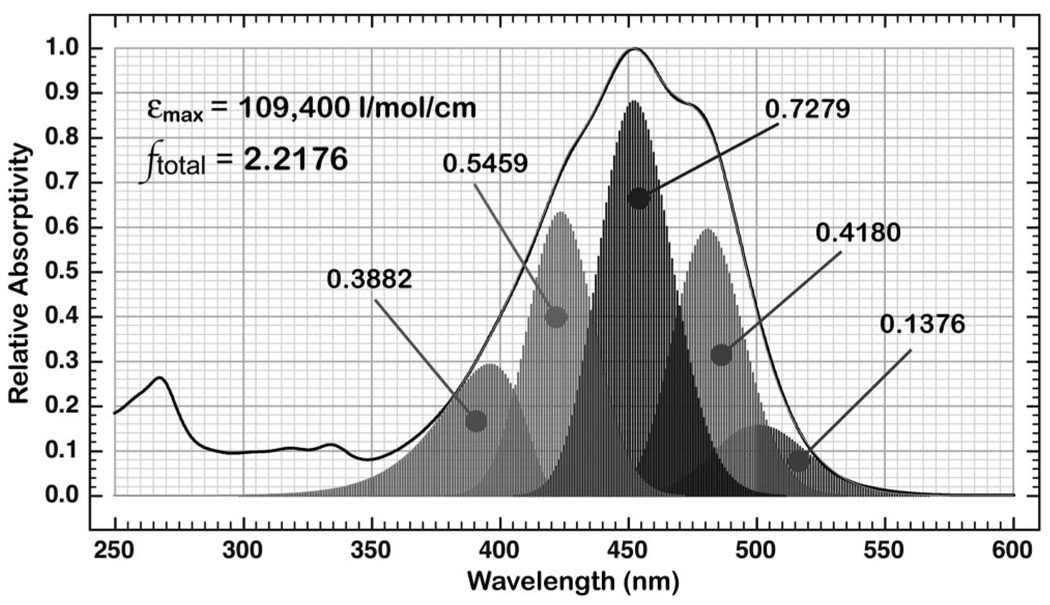
Analysis of the oscillator strength of the λ_max band of Fx based on a fit to five component log-normal bands. The oscillator strength contributed by each component band is indicated and the sum of all five bands yields a value of 2.2176.

Figure 6.

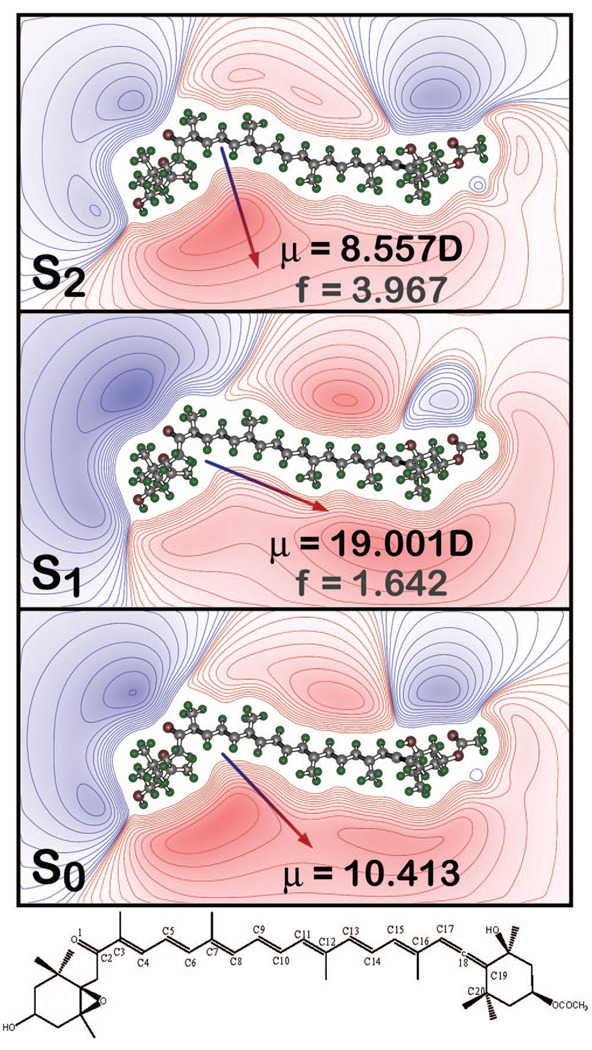
Charge shift upon excitation into the low-lying strongly allowed state based on the mulliken charges from the SACCI-CISD calculations. The arrows (head positive) indicate the dipole moment (S₀) or the changes in the dipole moments upon excitation (S₁ and S₂). Red contour lines indicate regions of excess positive charge and blue contour lines indicate regions of excess negative charge. The chemical stick figure of Fx is shown at the bottom. The distance between O1 (carbonyl oxygen) and C10 is ~9.5 Å and between O1 and C17 (of the allene) is ~18 Å.

Solvent Shift Analysis

The solvent shift analysis carried out on Fx is similar to that performed for peridinin where the difference in energy, hν̃_tot, between the condensed phase, hν̃_ab, and the gas phase, hν̃₀, reported in Table 6, is estimated from dipole reorganization energies and by treating the solvent as a dielectric continuum.^18,29 The solute is modeled as a polarizable point dipole in the center of an ellipsoidal or a spherical cavity. In contrast to the Onsager or Lorenz model,³³ the formulation used here from ref 47, to calculate the total solvent hν̃_ab, is exact to first order in polarizability. (The free energy cost for polarizing the medium (the self-energy) to equilibrate to the solute dipole, can also be determined from this formulation.) The theoretically evaluated solvent shifts relative to hexane, hΔν̃_hex, may be directly compared to the experimental values of hΔν̃^exp in Table 6. The semiaxes of the ellipsoid are set as a_x = 15 Å and a_y = a_z = 5 Å (see above). In a spherical cavity a radius of 15 Å, that is, a_x = a_y = a_z, is used to accommodate the long axis of Fx.

TABLE 6.

Solvent Shift Analysis for Fucoxanthin^a

	1	2	3	4	5	6	7	8	9
nb	1.37	1.374	1.498	1.41	1.40		1.359	1.53	1.34
∊0 b	1.9	1.895	2.275	5.4	7.6		20.7	25.2	35.9
λmax c0–1	446	450	461	451	459	446	443		447
λmaxc 0–0	477	478	485	475		473	467		470
hΔν̃expd 0–1	0	−200	−730	−249	−636	0	+151		−51
hΔν̃expd 0–0	0	−44	−346	+88	+ 177	+ 448			+ 312
		(I) μg = [−6.13, 5.55, −1.77], μe = μg + 5 D, αg = 129 Å3, and αe = 291 Å3
hν̃tote	−68	−68	−84	−141	−154		−177	− 179	−182
hΔν̃hex e	0	0.3	−16	−72	−86		−108	−111	−114
		(II) μg = [−6.13, 5.55, −1.77], μe = μg + 10 D, αg = 129 Å3, and αe = 291 Å3
hν̃tote	−214	−214	−245	−347	−371		−411	−415	−421
hΔν̃hex e	0	0.5	−31	−133	−157		−197	−201	−207

^aThe experimental solvents shifts are reported for: (1) n-hexane,²³ (2) 3-methyl pentane,¹⁵,⁷⁶ (3) benzene,⁷⁶,⁷⁷ (4) methyl tetrahydrofuran, (5) tetrahydrofuran, (6) petroleum ether,⁷⁶,⁷⁷ (7) acetone,23 and (9) acetonitrile. A variation of ± 0.2 nm corresponds to an energy difference of ca. (20–25 cm⁻¹. Benzonitrile (8), with intermediate solvent parameters^bis included for comparison.

^bThe refractive index (n) and the static dielectric constant (ε₀) are listed for the above solvents except petroleum ether.

^cThe experimental values for the 0–1 (absorption maxima) and the 0–0ands are listed in wavelength units (nm) for these solvents.

^dThe energy difference relative to n-hexane for these 0–0 and 0–1 bands, hΔν̃^exp, are listed in wavenumbers (cm⁻¹).

^eThe calculated energy difference between the condensed and gas phases and the shift relative that in hexane are reported as hν̃^tot and hΔν̃_hex, respectively. The solvent shifts are evaluated for Fx in an ellipsoidal cavity with semiaxes of 15 × 5 × 5 ų are evaluated using the ground-state dipole moment from MNDOCI calculations and by setting (I) μ_e = μ_g + 5 D and (II) μ_e = μ_g + 10 D, along the x direction (see Results). The ground- and excited-state polarizabilities are obtained from the MNDOCI calculations using an 8 × 8 basis ≈10 Å.

Results

Absorption Spectra of Fucoxanthin in MeTHF and FCP

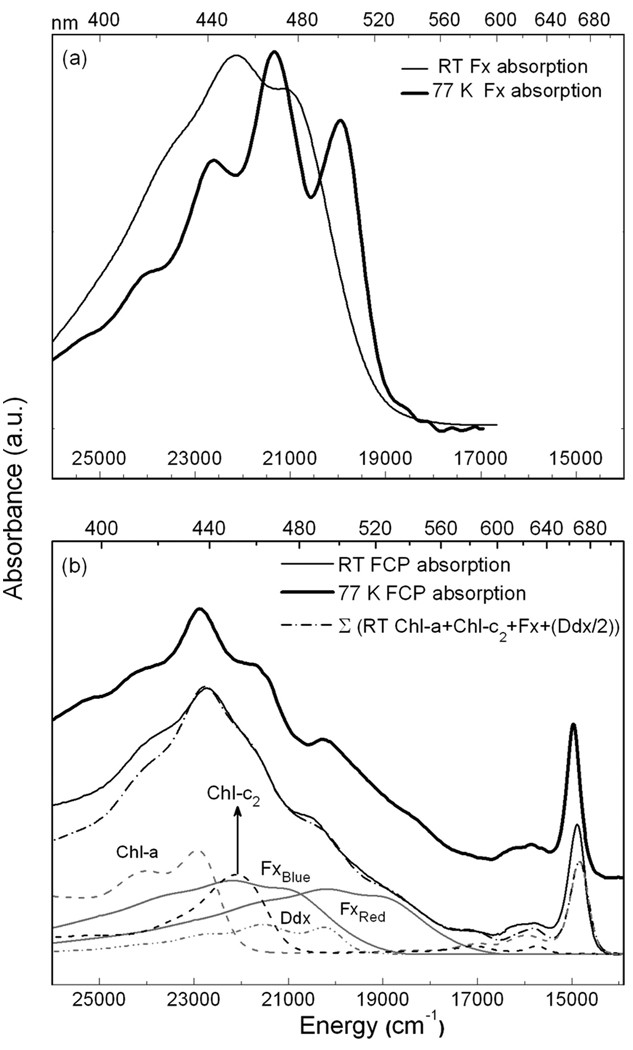
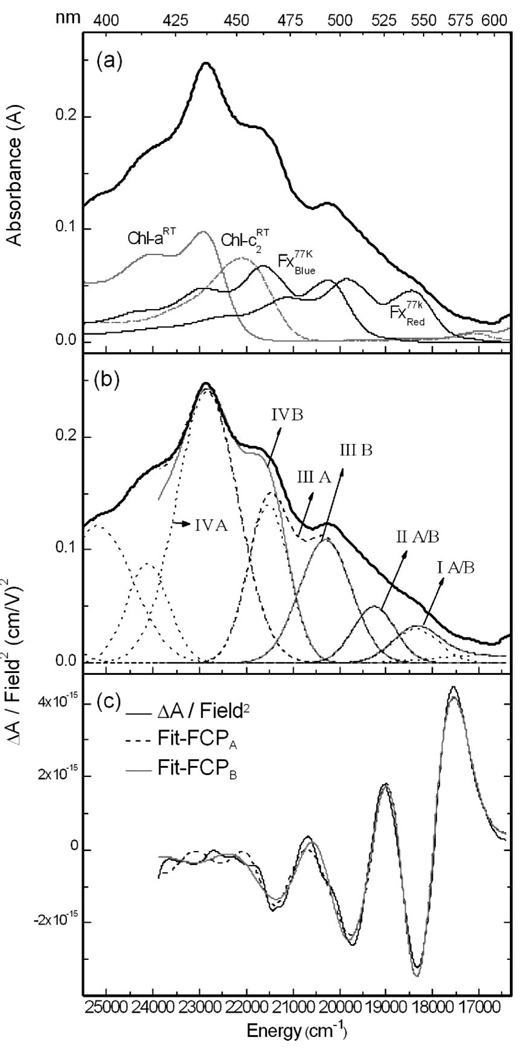
The absorption spectra of Fx in MeTHF and FCP are shown in Figure 1a and Figure 1b, respectively, at room temperature, rt, (dark-solid line) and at 77 K (light-solid line). Lowering the temperature to 77 K produces a large red shift in the absorption maximum of Fx from 451.5 to 468.5 nm (~800 cm⁻¹). Such an effect, observed in carotenoids^15,18 and other systems on glass formation of organic solvents and polymers,²⁴ may be used to understand environmental effects in the protein where similarly large red shifts are observed. The increase in resolution at 77 K reveals the 0–0 band of Fx at 501 nm, which was visible as a shoulder at rt (~479 nm). The vibronic progression, on the order of 1400 cm⁻¹, is typically a mixture of C=C and C–C stretching modes. Also visible, is a small absorption tail (>19000 cm⁻¹) that may be due to a conformer, or state, that is stabilized and/or gains oscillator strength at 77 K. Whether the tailing absorption at the red edge truly originates from a distinct state/species will be ascertained from the Stark spectrum.

Figure 1.

The absorption spectra at rt (light solid line) and at 77 K (dark solid lines) are shown in (a) for Fx in MeTHF and in (b) for FCP in glycerol/buffer glass. Also shown in panel b with a dot-dash line is the weighted sum of the rt absorption spectra of the constituent pigments, Chl-a in 80% acetone, Chl-c₂ in diethyl ether, and Fx in MeTHF, that have been shifted as listed in Table 3. The absorption of Ddx in 100% acetone was not shifted (λ_max = 465 nm).

In contrast to Fx, the absorption spectrum of FCP, composed of the overlapping absorptions of Fx, Chl-a and Chl-c₂ present in a stoichiometric ratio of 4:4:1, respectively,¹⁹ does not show significant differences between rt and 77 K. Nevertheless, the individual pigments may undergo changes that are not apparent in the overall absorption of FCP, because of the relatively small intensity of the individual pigment absorptions, or because shifts in the overlapping absorptions cancel each other out. Such may be the case in the carotenoid-absorbing region (400–550 nm) of the FCP spectrum. At 77 K, there is a loss in intensity around 480 nm with a concomitant increase in intensity around 490 nm, which may be attributed to a red shift of an underlying Fx absorption. Indeed, the 0-0 band of Fx in MeTHF at 77 K spectrum (dark solid line in Figure 1a) matches the shoulder that is evident at ~500 nm in the 77 K FCP spectrum (dark solid line in Figure 1b). Similarly, the shoulder at ~540 nm that is faintly evident in the FCP spectrum could occur because of the red shift of a more red absorbing Fx.

The effect of lowering the temperature in the chlorophyll absorbing regions is less pronounced than in the carotenoid region. In the Soret region, there is a 1–2 nm blue shift to 437 nm, which is accompanied by a similar 50–60 cm⁻¹ blue shift of the Chl-a Q_y band, from 672 to 668 nm. (Note that this FCP spectrum is obtained in a glycerol-buffer solution (55:45, v/w), where the addition of glycerol to the buffer solution shifts the absorption maximum by ca, −10 cm⁻¹ at rt.) The absorption between 600 and 640 nm primarily arises from Chl-a, and to a lesser extent from Chl-c₂. The Q_y band of Chl-c₂, which has a much smaller oscillator strength than that of Chl-a, is at ~630 nm and the Q_x band is at ~580 nm somewhat different from that in 90% acetone, where they are at 582.5 and 631, respectively.⁴⁸ In the 77 K spectra, a peak is clearly visible at 632 nm and can be attributed to the Q_y band of Chl-c₂. However, the Stark signal from this band is very weak, and is significantly overlapped with Chl-a vibronic bands, which prevents us from obtaining reliable electrostatic parameters for the Q_y band of Chl-c₂.

To better locate the individual carotenoid and chlorophyll absorptions, and to estimate their electronic influence in a given energetic region, a simple fit to the absorption line shape of FCP at rt is generated using the pigment absorptions in solution (compare light-dash line to light solid line in Figure 2b). Although there are nine pigments, four absorption spectra, one each of Chl-a and -c₂ and two of Fx, suffice to reproduce the absorption of FCP. (Lacking additional information regarding the molecular structure and local environment about all the pigments, it would be too speculative to introduce more degrees of freedom to model nine pigment absorption bands.) The rt spectra of the pigments were shifted and weighted simply by using their absorptions in solution, without recourse to a rigorous algorithm (Table 3). Guidelines for the relative pigment intensities were obtained from stoichiometric analysis of the FCP complex in ref 8. Multiplying the extinction coefficients, normalized by the molecular weights, by the 4:4:1 stoichiometric ratio for Fx:Chl-a:Chl-c₂, suggests relative intensities of 1.00: 0.58:0.56. In the fit to the absorption of FCP at rt, a ratio of 1.00:0.66:0.54:0.10 is obtained for the intensities of Fx:Chl-a: Chl-c₂:Ddx (Figure 2b), which is in reasonable agreement with the ratio of 1.00:0.60:0.63:0.10 obtained using the exact stoichiometric ratio.⁸ The solvent spectra of the pigments have been shifted in wavenumbers, which is linear in energy, rather than in nonlinear wavelength units. The absorption spectra of Chl-a in 80% acetone (λ_max = 432 nm) and Chl-c₂ in diethyl ether (λ_max = 451 nm) have been shifted by −215 and −110 cm⁻¹, respectively, whereas that of Fx in MeTHF (λ_max = 452 nm) has been shifted by +50 cm⁻¹ (Fx_blue) and by −2000 cm⁻¹ (Fx_red). These values are listed in Table 3. The positioning of the Chl-a spectrum, based on the goodness of fit to the absorption of FCP in the Soret region, results in the Q_y band of Chl-a in solution (λ_max = 664 nm in 80% acetone) being offset from that in the protein by ca. −40 cm⁻¹ (gray dashed line, which overlaps the dot-dash line in Figure 1b). This mismatch of the Soret and Q_y band energies in the two environments could arise if these two electronic transitions have different electrostatic properties, which would result in different solvation energies of each band in the protein environment.

Figure 2.

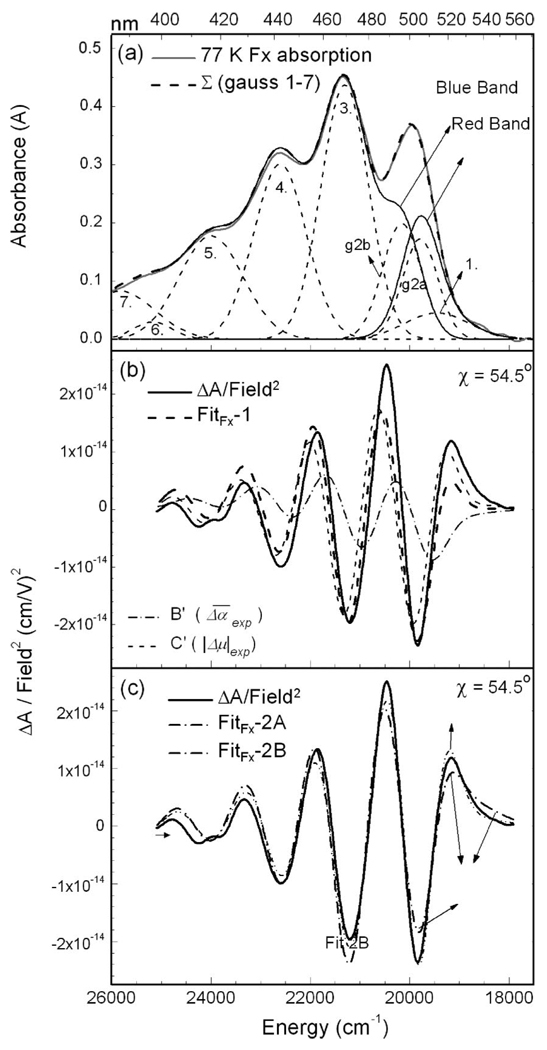
In (a) the absorption spectrum of Fx in MeTHF glass at 77 K is shown in light-gray line, along with the gaussians that model the absorption (light-dotted line numbered 1–5) and the sum of these gaussian functions (dark-dashed lines). (b) Fit_Fx-1: the field-normalized Stark spectrum (dark solid line), fit (dark dashed line), first- (B′ in light dot-dash line) and second- (C′ in light dashed line) derivative components of the fit to the Stark spectrum are shown at χ = 54.5° (see eq 1). In panel c, the Stark signal (dark solid line) is fit by deconvolving the absorption into two bands: in Fit_Fx-2A the two bands correspond to gaussian 1 and to the sum of gaussians 2–5. In Fit_Fx-2B, the two bands correspond to the sum of gaussians 1 and “g2a” (red band in panel a) and to the sum of gaussians “g2b”–5 (blue band in panel a).

TABLE 3.

Absorption Maxima of Pigments in Solution and in the Fits

	ν̃max (λmax)a	ν̃max (λmax)b	ν̃max (λmax)
Fxcin MeTHF rt	22123 (452)	22168 (451)
		20157 (496)
Fxc in MeTHF 77 K	21322 (469)		19823 (505),
			21618 (463)d
			20322 (492),
			19572 (510)e
Chl-ac Soret rt	23148 (432)	22927 (436)	22927 (436)
Chl-ac Qy rt	15060 (664)	14838 (674)	14838 (674)
Chl-c2 c Soret rt	22173 (451)	22077 (453)	22077 (453)
Chl-c2 c Qy rt	15848 (631)	15740 (635)	15740 (635)

^aRoom temperature (rt) absorption maxima of the pigments in FCP are reported in wavenumbers (ν̃_max) and in nm in parentheses (λ_max).

^bThe maxima of the shifted pigment spectra used to fit to the rt absorption of FCP (Figure 1b).

^cThe pigment absorptions are of fucoxanthin in methyl tetrahydrofuran (MeTHF), Chl-a in 80% acetone and Chl- c₂ in diethyl ether.

^dThe maxima of the shifted 77 K-absorption spectrum of Fx used to fit the 77 K spectrum of FCP in Figure 3a

^eThe maxima of the two additional 77 K-Fx spectra used to fit the Stark signal in Figure 4.

Stark Spectrum of Fx in MeTHF

In Figure 2, the fits to the Stark spectrum of Fx in MeTHF obtained by two different methods are shown. The absorption spectrum is first fitted to a sum of 7 gaussians to obtain a smooth line shape and a better fit to the Stark spectrum. The 4 most intense gaussians are centered at ~ 19950, 21300, 22600, and 24000 cm⁻¹, in general agreement with Frank et al.¹⁵ An additional low-intensity gaussian was included to better reproduce the shape of the absorption spectrum at the red edge (~18700 cm⁻¹). The gaussians at ~ 25400 and 25800 cm⁻¹, although not used in any of the fits to the Stark spectrum, are included for completeness. The weighted sum of the derivatives of the absorption line shape is then fit to the Stark signal. This fit, Fit_Fx-1, makes use of a single function, A(ν̃) (eq 1), to model the absorption. The overall shape and magnitude of the Stark spectrum are well reproduced above 20500 cm⁻¹, and the electronic properties from this fit are reported in Table 1. The fit to the red edge (18000–20500 cm⁻¹) is treated separately below. The change in static dipole moment (|μ⃗|_exp) obtained from this fit is 17 ± 0.8 D, which although somewhat smaller than that of peridinin,¹⁸ attests to the previously unknown charge-transfer character of the S₀ → S₂ transition of Fx. In addition, a value of 0.92 ± 0.7 is obtained for m̂•Δμ⃗|/|Δμ⃗|, indicating that the angle between the transition-dipole and (static) difference-dipole moments is ~20°. The experimental parameter corresponding to the change in polarizability, ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$, is found to be −700 ų. The large negative value of ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$ suggests a contribution from A_ij (eq 5), and is discussed below.

Electrostatic Properties of Red-Edge Absorption of Fx

As noted above, the fit at the red edge is poor, and the amplitude of the Stark signal is visibly greater than the fit (compare dashed and solid lines in Figure 2b) suggesting that the CT character at the red edge is larger than that obtained from Fit_Fx-1. To determine the unique electronic properties of the red-absorbing state, the absorption in this region is separated from the main band, and the Stark spectrum is fit to two A(ν̃) functions.^18,24 Two sets of a_χ, b_χ and c_χ values are obtained from this fit and the electronic properties of each band are determined. The Stark spectrum is first fit simultaneously to gaussian 1, and to the sum of gaussians 2–5 (Fit_Fx-2A in Figure 2c). A |μ⃗|_exp value on the order of 40 D is obtained for gaussian 1 and the higher-energy band, the sum of gaussians 2–5, exhibits a slight decrease from 17 D (Fit_Fx-1) to 15 D. However, the maximum and minimum of the Stark signal at the red edge are still not well reproduced (Fit_Fx-2A in Figure 2c), and a better fit is possible if the influence of the red transition is extended further into the main absorption band, for instance, by modeling a broader and/or more intense red absorption. Gaussian 2 (ν_max = 19950 cm⁻¹) was thus arbitrarily separated into two bands (denoted “g2a” and “g2b” in Figure 2a), such that g2a was summed with gaussian 1 to model the red-edge transition (red band in Figure 2a), and the sum of the remaining gaussians (g2b to 5) models the main band (blue band in Figure 2a). Indeed, Fit_Fx-2B is better than Fit_Fx-2A (see Figure 2c). The 16 D |Δμ⃗|_exp for the blue band is similar to that from Fits_Fx-1 and -2A, whereas the 22 D |Δμ⃗|_exp for the red band is much smaller than that obtained in Fit_Fx-2A. The red band is less strongly overlapped with the blue band in Fit_Fx-2B, and the parameters obtained from this LLSQ fit less over-determined, and therefore more reliable than from Fit_Fx-2A.

For Fx in MeTHF, the discrepancy in the 1-band fit is much less pronounced than for peridinin in ethylene glycol (EG)¹² and is clearly localized at the red edge. The glass is formed by “instantaneous” immersion in LN2 using freshly distilled MeTHF, decreasing the likelihood of trapping a thermodynamically unfavorable conformer. In contrast to the hydrogen-bonding environment of EG, which was expected to promote the formation of ground-state conformers, the small, aprotic MeTHF molecules are not expected to do so. Moreover, the value of |m̂•Δμ⃗|/|Δμ⃗| ratio is ~ 0.91 for both the red and blue bands of Fx (Table 1) suggesting that the species that give rise to the absorptions are not distorted, and maintain an all-trans conformation in the MeTHF glass. Therefore, the red-edge absorption (19000–21000 cm⁻¹), which differs electronically from the bulk, likely originates from a low-energy vibronic or electronic state.

Stark Spectra of FCP

In Figure 3, the absorption and Stark spectra of FCP at 77 K are shown. A priori, the Stark spectrum of FCP cannot be fit to the absorption to yield a single set of |Δμ⃗|_exp and ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$ values, because the absorption between 17000 and 26000 cm⁻¹ does not originate from a single entity in a uniform environment, but from nine pigments. The fit to the FCP absorption at rt (Figure 1b) suggests that at least four of these pigments, 2 Fx’s, 1 Chl-a, and 1 Chl-c₂, have distinct electronic properties. Differences between the electrostatic properties of the two other Fx’s, and three other Chl-a’s, may be manifested in the Stark spectrum, despite their presumably similar absorptions. To determine the origin of the Stark spectrum in a given energetic range, the rt Chl spectra, same as in Figure 1b, and the 77 K Fx spectrum shifted by +300 cm⁻¹ (Fx_red) and −1500 cm⁻¹ (Fx_blue), the sum of which is close to the 77 K FCP absorption, are superimposed on the 77 K absorption of FCP (Figure 3a).

Figure 3.

In panels a and b, the absorption spectrum of FCP at 77 K in glycerol/buffer glass (dark-solid line) is shown in the region of Fx and Chl Soret absorptions, onto which is superimposed the rt spectra of Chl-a in acetone and Chl-c₂ in diethyl ether (Figure 1b) and the 77 K absorption of Fx in MeTHF (λ_max = 469 nm) shifted by +300 cm⁻¹ (Fx_blue) and −1500 cm⁻¹ (Fx_red). In panel b, the absorption spectrum of FCP is deconvolved into two sets of four bands: IA–IVA (dashed lines) and IB–IVB (dark-solid gray lines) (see Results). Also shown are the gaussians (light dotted lines) used to fit the absorption spectrum. (c) The field-normalized Stark spectrum at χ = 54.5° (dark-solid line) and the fits to the spectrum using bands IA–IVA (Fit-FCP_A in dashed line) and bands IB–IVB (Fit-FCP_B in gray solid line) are shown

The FCP absorption is first fit to (nine) gaussians (see light dotted lines in Figure 3b) and then broken up into bands that are composed of one or more of these gaussian functions, to fit the Stark signal.^24,30 Two equally good fits to the Stark spectrum, FCP_A and FCP_B (Figure 3c), can be obtained using four bands generated from two different combinations of gaussians. In both Fit-FCP_A and -FCP_B, the first two bands, I and II, are the same (Figure 3b). Band I is the sum of the first two gaussians, and II is the third Gaussian. Bands III and IV can however be constructed in two different ways: for Fit-FCP_A, band IIIA is the sum of gaussians 4 and 5, and band IVA the sum of gaussians 6 and 7, and for Fit-FCP_B, band IIIB is gaussian 4, and IVB is the sum of gaussians 5, 6, and 7. Note that the Stark signal below 450 nm is nearly zero and very noisy and the solution to the fit in this region corresponding to Chl-a and partly to Chl-c₂, is not reliable. Fits-FCP_A and -FCP_B, obtained using 12 free parameters (four a_χ, b_χ, and c_χ’s), yield distinct |Δμ⃗|_exp and ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$ values for bands I–IV (Table 2). Bands I, II, and III, situated between 16000 and 22000 cm⁻¹, encompass the region where the Fx’s absorb (Figure 3a) and the absorption of the Chl’s (21000–24000 cm⁻¹) is primarily contained in band IV (A and B). However, in Fit-FCP_A, most of the Chl-c₂ absorption is enveloped by band IIIA, in which its electrostatic properties will be primarily manifested. Whereas, the results for band IVB will be influenced by Fx_blue (Figure 3a).

In Fit-FCP_A (dashed line in Figure 4c), the largest change in dipole moment, on the order of 37–45 D, is obtained for band IA (18000–19000 cm⁻¹), whereas a significantly smaller change in dipole moment on the order of 4–7 D is obtained for band IIA (19000–21000 cm⁻¹). The |Δμ⃗|_exp value for IIIA (>21000 cm⁻¹), on the order of 14–17 D, is similar to that for Fx in the MeTHF glass (Fit 1 in Table 1). In Fit-FCP_B (gray solid line in Figure 3c) the properties of band IB, corresponding to the red-absorbing Fx, are the same as in Fit-FCP_A. However band IIB now has a much larger |Δμ⃗| on the order of 12 D. Although band IIB is the same as IIA, the weighting of the fit parameters are dependent on the shape and intensity of the adjacent band. Indeed, band IIIB is smaller than IIIA and Fit-FCP_B yields a |Δμ⃗|_exp of ~16 D for IIIB, which is much larger than for IIIA and similar to that found for Fx in MeTHF. Note that Chl-c₂ absorption does not contribute to IIIB as it does to IIIA. The results for band IV, which primarily corresponds to chlorophyll (Soret) absorption, has a small Stark signal, is quite noisy, and the |Δμ⃗|_exp values, on the order of 4 D, are less reliable than for the lower energy bands.

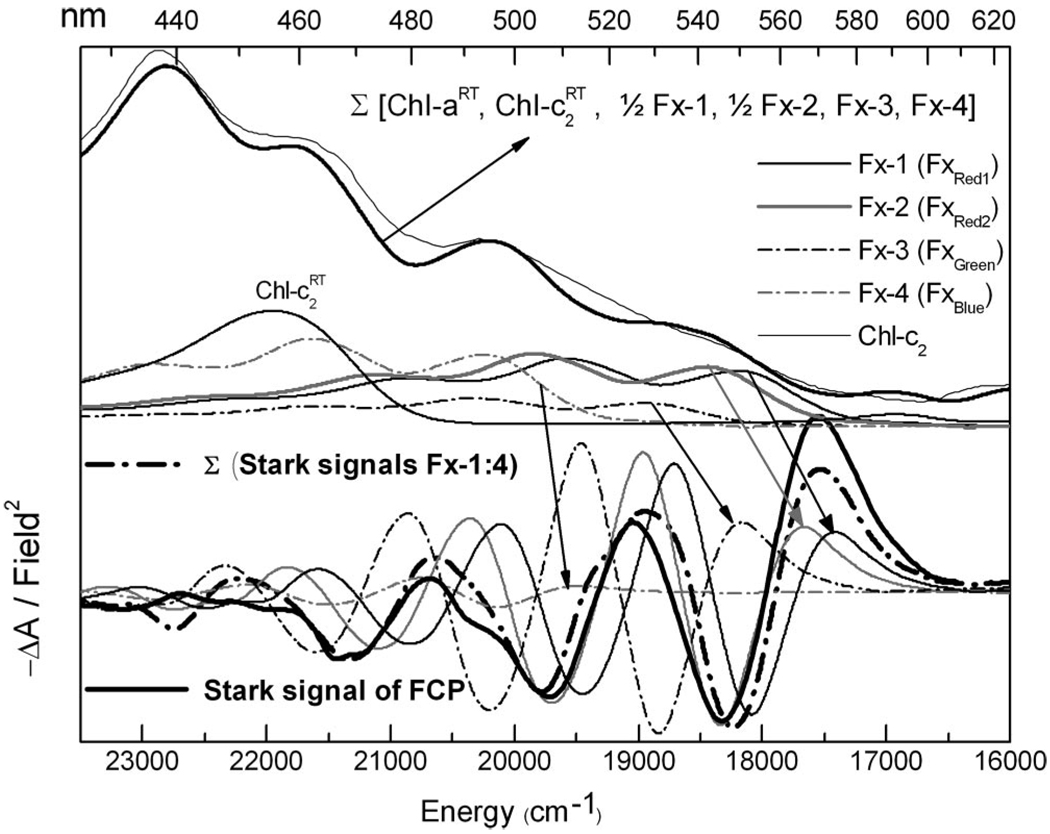
Figure 4.

At the top are shown the absorption spectrum of FCP (light-solid line) and sum (dark-solid line) of the rt Chl spectra and four weighted and shifted 77 K spectra of Fx in MeTHF. The absorption of Chl-c₂ (light-solid line) and the four Fx spectra (λ_max = 511, 505, 492, and 463 nm), which correspond to the scaled and shifted Stark spectra of Fx, relative to that in MeTHF (Table 1), are shown in the bottom half of the figure (see arrows). The absorption and Stark spectra of these four Fx’s are Fx-1 in black solid line, shifted by −1750 cm⁻¹; Fx-2 in gray solid line, −1500 cm⁻¹; Fx-3 in black dot-dash line, −1000 cm⁻¹; and Fx-4 in gray dot-dash line, +300 cm⁻¹ (Table 3). The sum of these four Stark spectra (dark dot-dash line) closely matches the Stark spectrum of FCP (dark-solid line) shown below (see Discussion).

The experimental parameter of ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$ (eq 5) of these bands are listed in Table 3 and vary between −1500 ų for band I and 30 ų for band IV. The values of ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$ for bands II and III vary significantly between Fit-FCP_A and Fit-FCP_B and do not offer a useful physical parameter for analysis. The non-physical values of ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$ are typical of where overlapping bands are fit to the Stark spectrum^24,30 but are included here for completeness.

In contrast to the Soret band, the Stark signal of the Chl-a Q_y band (Supporting Information) has a much higher signal/noise ratio because of its narrowness, and higher lamp output. Indeed, the fit to the Q_y absorption unambiguously yields a change in dipole moment |Δμ⃗|_exp of 0.92 ± 0.2 D and a ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$ of 20 ± 5 ų. There is some asymmetry in the fit at the red edge (14500–14800 cm⁻¹), which suggests the presence of another Chl-a.^8,19,20 However, the deviation from the fit is small, indicating that the electrostatic properties of the red-edge Chl-a are on the same order of magnitude as that of the bulk of the Chl-a’s. Attempts to fit the Stark spectrum, by modeling a second Q_y transition at the red edge, did not yield physically reasonable parameters for the lower energy band and was not pursued further.

Calculations on Fucoxanthin

The properties of the two lowest-lying excited singlet states as calculated by the various molecular-orbital methods are summarized in Table 5. Using the same B3LYP/6-31G(d) minimized energy geometry, the various methods consistently yield a relatively large value of 9 D for the ground-state dipole moment of Fx. The description of the excited states however differ in the energies and dipolar properties calculated for the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like (S₁) and the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like (S₂) states. The MNDO-PSDCI calculations predict a lowest-lying $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state with a small oscillator strength (f_osc ≈ 0.022) where the separation between the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state and the excited $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state, based on the CISD calculation, is ~800 cm⁻¹ (Table 5). A coupled-cluster perturbative calculation increases the calculated separation to ~2200 cm⁻¹ and predicts a drastic lowering of the oscillator strength of the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state to 0.022, from 0.47 (MNDOCI⁺ in Table 4).

TABLE 5.

Key Configurations for Excitation into the Two Lowest Excited Singlet States^a

single excitations		double excitations
excitation	eigenvector	excitation	eigenvector
	Key Excitations into the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$ -like State
HOMO→LUMO	0.6183	HOMO→LUMO; HOMO→LUMO	0.4041
HOMO−1→LUMO	0.2937	HOMO→LUMO+1;HOMO−1→LUMO	0.2520
HOMO→LUMO+1	−0.2693
HOMO−1→LUMO+1	0.2068
	Key Excitations into the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$ -like State
HOMO→LUMO	0.7028	HOMO→LUMO; HOMO→LUMO	−0.3226
HOMO−1→LUMO	−0.3275	HOMO→LUMO; HOMO−1→LUMO	0.1621
HOMO→LUMO+1	0.2790	HOMO→LUMO+1; HOMO→LUMO	−0.1431

^aThe key singles and doubles configurations, from MNDO-CI calculations for excitation into S₁ ($2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$ -like) and S₂($1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$ -like) show that 39.8% of $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$ -like state excitations and 26.7% of $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$ -like state excitations were double excitations. These configuration do not include contributions of less than 2% to either excitation.

TABLE 4.

Calculated Properties of the Two Lowest-Lying Excited Singlet States of Fucoxanthin

theoretical method			μg S0 (D)	ΔE $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$ (eV)	fosc $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$	ΔE $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$ (eV)	fosc $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$	Δμ $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$ ←S0(D)	Δμ $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$ ←S0(D)
MNDOCIa	AM1	Slater	8.461	2.628	0.471	2.728	2.532	+ 8.755	−2.365
MNDOCIb	AM1	Slater	8.461	2.541	0.158	2.690	2.697	+ 5.969	+ 0.820
MNDOCI+c	AM1	Slater	8.453	2.432	0.022	2.712	2.910	+ 2.737	+ 4.050
SACCI-CISDd	RHF	D95	10.41	3.796	1.642	3.967	3.263	+ 9.869	−3.502
TD-DFTe	PBE1 PBE	6-31G(d)	8.984	3.107	0.216	2.468	3.594	−1.850	+ 19.55
TD-DFTe	B3LYP	6-31G(d)	9.041	2.941	0.294	2.398	3.447	−3.902	+ 14.60
TD-DFTe	SVWN	6-31G(d)	9.364	1.933	0.004	2.087	2.197	+ 33.10	+ 46.68
expt f				~ 2.4	<0.2	2.737	2.218

^aFull single and double CI for an orbital basis set of the eight highest energy occupied and eight lowest energy unoccupied π orbitals plus single CI involving the three highest energy occupied σ and single lowest energy unoccupied σ orbitals (CISD 8π × 8π + CIS 3 × 1 = 99 singles + 2048 doubles).

^bAs in footnote a but with CISD 9π × 9π + CIS 3 × 1 = 120 singles + 3080 doubles.

^cAs in footnote a but with partial inclusion of quadruples via coupled-cluster perturbation.

^dSACCI-CISD based on the 52 highest energy occupied and 52 lowest energy unoccupied orbitals with full single and partial double CI (2704 singles + 15939 doubles).

^eExcited state dipole moments are calculated by using the one-particle CI density.

^fTransition energies (ΔE ≈ 8062 cm⁻¹) and oscillator strengths (f_osc) based on fucoxanthin in THF assuming molar absorptivity of 109400 L/mol/cm.⁷⁵ The transition energy of the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$ -like state is estimated on the basis of fluorescence studies.

Using the calculated oscillator strengths and the transition energies, the absorption band of Fx is fit to a five-component log-normal set of vibronic bands. The sum of the oscillator strengths of the component bands yields a value of 2.218 (Figure 5). Note the presence of the small band at ~500 nm (f_osc = 0.138), which may be associated with the lowest-lying “forbidden” $2^1{A}_g^{*-}$-like state. A portion of the intensity of the highest energy band (f_osc = 0.388) may be associated with a higher energy state. If both assumptions are correct, the oscillator strength of the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state may be as low as 1.89. This analysis suggests that the oscillator strength of the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state is between 1.89 and 2.22 (Table 4), which corresponds to a transition dipole moment between 13.5 and 14.6 D.

The key values obtained from the calculations, relevant to the current study, are the dipolar properties of the two lowest excited singlet states, which are listed in Table 4, relative to the ground-state value calculated for a given method. Although the MNDO-PSDCI calculations predict that the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state has a larger dipole moment in all cases explored, the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state is calculated to have a dipole moment smaller than the ground-state when the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state is nearby. The SACCI calculations were limited to single and double CI and mirror the standard MNDO-PSDCI calculations. In Figure 6, the charge shift upon excitation into the low-lying strongly allowed $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state is shown for the MNDO-PSDCI calculations using an 8 × 8 basis π-orbital set, and the arrow indicates the direction of the net shift of electron density on excitation. A net shift in negative charge away from the carbonyl group is responsible for lowering the dipole moment of the excited state. When a larger (9 × 9) basis set CISD calculation is carried out within MNDO-PSDCI theory, contributions from additional double excitations reverse this charge shift and yield an enhanced dipole moment for the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state (Table 4). Hartree–Fock (HF) CISD methods are thus somewhat ambiguous about the dipole moment change upon excitation into the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state. In contrast, due to the importance of doubly excited configurations, the lowest-lying ”forbidden” $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state is consistently predicted to have a large dipole moment.

Besides the static dipole moment, the polarizabilities have also been calculated and are listed below for the ground and first two excited singlet states, with the xx, yy, and zz components in parentheses:

$$\begin{array}{cc}\hfill \mathrm{\alpha }({\mathrm{S}}_0)\hfill & \hfill =129.25{\mathrm{\AA }}^3(246.22,81.66,59.88)\hfill \\ \hfill {\mathrm{\alpha }}^{*}(S_0)\hfill & \hfill =49.84{\mathrm{\AA }}^3(135.30,12.87,1.33)\hfill \\ {\mathrm{\alpha }}^{*}(2^1{\mathrm{A}}_{\mathrm{g}}^{*-}-\text{like})\hfill & =149.11{\mathrm{\AA }}^3(434.99,11.67,0.68)\hfill \\ {\mathrm{\alpha }}^{*}(1^1{\mathrm{B}}_{\mathrm{u}}^{*+}-\text{like})\hfill & =251.56{\mathrm{\AA }}^3(720.65,32.23,1.80)\hfill \end{array}$$

where the electronic polarizabilities indicated by α* are for the π-system only.

The fact that the MNDO-PSDCI calculations indicate that the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state has an extremely large polarizability of 251.56 ų, relative to the ground state (129.25 ų), is notable. In contrast, the polarizability of the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state is only 149.11 ų. Because all of the reported experiments are on a chromophore in solution, or in a protein, the polarizability of the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state may be manifested in the measured values of the static dipole moments, via interaction with the solvent reaction field.

A TD-DFT study was also carried out to provide contrast and perspective on the above Hartree–Fock calculations (Table 4). Three functionals that were used to explore different levels of correlation include, PBE1PBE, B3LYP, and SVWN (also called LSDA).^{43–45,49–57} The SVWN functional provides enhanced electron correlation and is the only functional that generates a lowest-lying $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like. However, this functional overcorrelates the excited states and the two lowest-lying singlet states are predicted at energies nearly 0.6 eV (~5600 cm⁻¹) too low for Fx. In contrast, our studies on carotenoids find that the PBE1PBE method is the best choice for studying the allowed states of carotenoids.⁵⁸ Whereas, this functional yields a reasonable value for the transition energy of the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state, its oscillator strength is overestimated. A key problem with TD-DFT methods is its tendency to overestimate the charge-transfer character of electronic transitions in large, conjugated polar molecules⁴³ and the estimation of the dipole moment for the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state, a priori, is expected to be quite large. Indeed, these calculations predict dipole moment changes into the low-lying strongly allowed $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state that are significantly larger than those predicted by the Hartree–Fock (HF) methods (SAC-CISD and MNDO-PSDCI). Nevertheless, the dipole moment changes of 15–20 D obtained by using the PBE1PBE and B3LYP functionals are actually in better agreement with the experimental results. Notably, the dipole moment of the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state is smaller than the ground-state when it is calculated to be above the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state, but larger if it is below the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state (SVWN functional). The dipole moments for the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like and $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like states from the latter calculations are in fact significantly larger (30–45 D) than in the ground state (Table 4). In contrast, both semiempirical and ab initio HF calculations, where the ordering of the states is correctly predicted, a majority of the dipole moment change upon excitation is found between the ground-state and the lowest-lying $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state. Note that the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state also exhibits an increase in dipole moment in these HF calculations, if the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state is lowered in energy. However, the nature of this coupling is not fully understood.

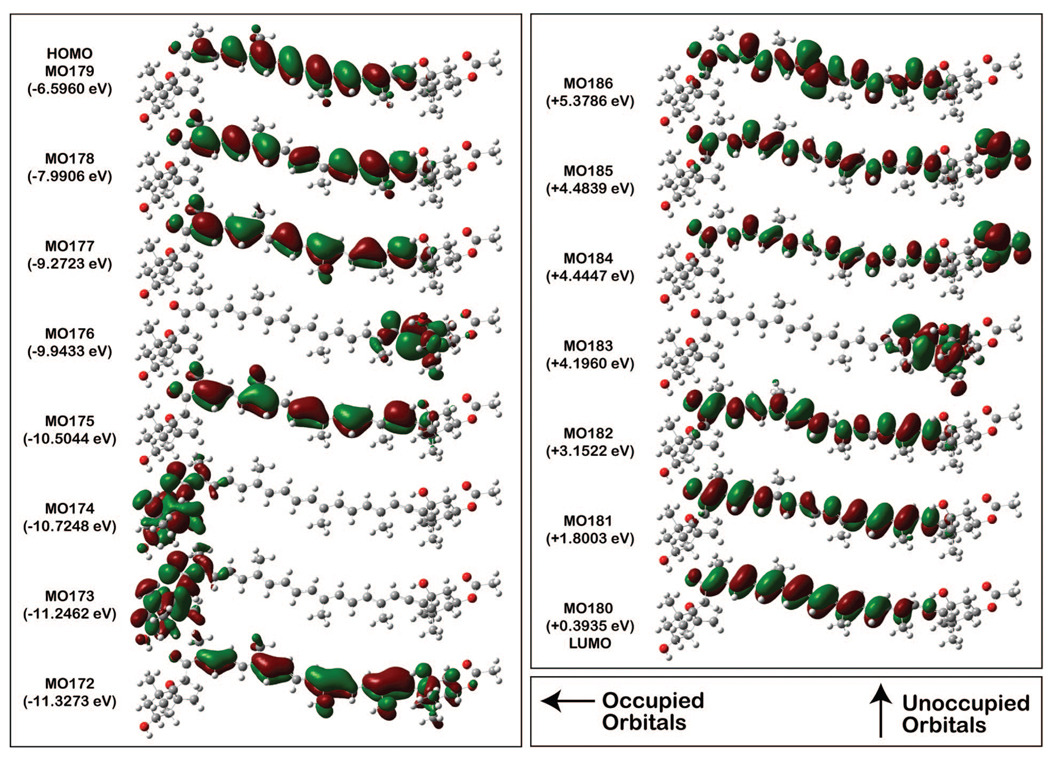
Because of the importance of double CI in describing the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state, we will limit our analysis of the configurational characteristics to the MNDO-PSDCI and SAC-CI methods, which both include doubles. The configurational properties for the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like and the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like states from SAC-CI calculations (Table 5) indicate remarkable similarities: the key single and double configurations are identical, and many of the secondary configurations match. Of the single excitation promotions that contribute to the S₀ → S₂ transition, ≈ 50% is from the highest-occupied molecular orbital (HOMO) to the lowest-unoccupied MO (LUMO), and an additional 20% of the transition originates in the HOMO and terminates in the LUMO. Double excitations account for much of the remaining 30% of promotions. Note too, that the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state has roughly 13% more double character than the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state, and this is responsible for its lower energy and lower oscillator strength. In Figure 7, the occupied and unoccupied molecular orbitals based on the D96 orbitals used in the SACCI-CISD calculations, which are visually similar to the Slater orbitals used in the MNDO-PSDCI calculations, are shown. Note that the three highest-energy occupied, and three lowest-energy unoccupied, MOs are π orbitals that exhibit electron densities that are fairly evenly distributed along the polyene chain. These orbitals are the primary orbitals involved in the low-lying electronic states (Table 5). Calculations also show that the π-orbitals of the allene group are fully rotated and oriented perpendicular to that of the polyene backbone and do not participate in the spectroscopy of this carotenoid. The localized π system of the allene is orthogonal to the polyene π system and the small amount of electron density (<0.05%), of the polyene π orbitals on the allene carbons, are a spillover into the σ system, identical to that which occurs for the methyl groups.

Figure 7.

Occupied (left) and unoccupied (right) molecular orbitals based on the D95 orbitals used in the SACCI-CISD calculations. These are visually similar to the Slater orbitals used in the MNDO-PSDCI calculations.

Solvent-Shift Analysis

The solvation energies for the gas-phase electronic energies are calculated using the gas-phase dipole moments and polarizabilities for the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like and the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like states from MNDOCI calculations (Supporting Information). Using the results from the MNDOCI calculations, where the dipole moment of the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state is less than the ground state (8 × 8 basis of π orbitals), there is a shift to higher energy with increasing solvent polarity, which is opposite to the experimental results for the absorption maximum. In contrast, the calculated solvent shifts indicate a decrease in energy with increasing solvent polarity, in agreement with experiment, when the dipole moment of the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state is greater than that of S₀ (9 × 9 basis set). However, the hΔν̃_hex values for the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state were much smaller than experiment. Clearly, μ_e must be greater than μ_g to match the experimental shift of the absorption maximum (0–1 band), with increasing solvent polarity (Table 6). Solvent shifts were thus evaluated to obtain the best match to experiment by setting the value of μ⃗_e by arbitrarily augmenting the value of μ⃗_g, first by 5 D and then by 10 D, along the x-axis direction. The shifts relative to n-hexane (hΔν̃_hex) were then calculated²⁹ and compared to the experimental values for the solvents listed in Table 6. We find that a 5 D Δμ yields solvent shifts that are generally smaller than experiment, but mimic the shift in acetonitrile relative to n-hexane. In contrast, the 10 D value incorporated for Δμ is in agreement with the solvent shift seen for MeTHF relative to n-hexane.

Discussion

The Electronic Properties of the S₂ State of Fx in Solution

The main visible transition in Fx, the symmetry allowed $1^1{\mathrm{A}}_{\mathrm{g}}^{-}-\text{like}\to 1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like (S₀ → S₂), is a typical, broad carotenoid band with distinct vibronic features. In MeTHF, the fit to the Stark spectrum of Fx yields an absolute value of 17 D for the change in dipole moment (|Δμ⃗|_exp) between the ground-state and the Franck–Condon region of the S₂ state, thus characterizing the S₀ → S₂ transition as a charge-transfer (CT) transition. Whether μ_e > μ_g, cannot be determined from the Stark signal and is instead inferred from the shift of the absorption to lower energy with increasing polarity, both in solution^14,59 and on the formation of the MeTHF glass at 77 K (Table 1). Therefore the calculated value of 9 D for μ_g (Table 4) implies a μ_e of at least 24 D, when accounting for a cavity-field enhancement by 10%. A 17 D |Δμ⃗|_exp implies that one unit of charge is transferred over 3.5 Å on photon absorption by Fx. On the basis of electronegativities, the likeliest electron acceptor is the oxygen of the carbonyl group (O1 in Figure 6). Therefore, charge shift from the “center of mass” of charge, localized over the polyene backbone in the ground state (Figure 7), to O1, suggests that ~0.35 units of a charge is transferred over ~10 Å.

The dipole moments from MNDOCI and SACCI calculations however predict very small changes in dipole moment on excitation into the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state, and furthermore the dipole moment of $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state is smaller than in the ground state. Given that the electron densities of the key molecular orbitals that contribute to the S₀ → S₂ transition are distributed along the polyene chain, these promotions will not produce a significant change in dipole moment (Figure 6). A Mulliken charge density difference analysis of the SAC-CI results (Supporting Information) provides insight into the origin of the discrepancy of the dipole moment differences. The carbonyl group, which is conjugated into the π-system of the polyene backbone, is a strong electron-withdrawing group and it is surprising that there is no noticeable increase in negative charge predicted for O1 on excitation into the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state. Instead, the charge density difference is localized in the center of the polyene backbone with a large oscillation in charge-density difference, from positive to negative, between adjacent carbons atoms in the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state. Whereas, in the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state, the oscillating charge density difference in the central part of the polyene backbone is accompanied by a small but distinct net shift in charge from the allene end of the polyene backbone toward the carbonyl oxygen (see Supporting Information). In contrast to the MNDO-PSDCI and SAC-CI results, the TD-DFT calculations do identify the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state as the one that possesses CT character (Table 4), where the shift in charge is from the allene group toward the carbonyl oxygen, rather than strong oscillatory changes in charge differences in the central part of the polyene backbone, (see Supporting Information) and accounts for the large dipole moment in the TD-DFT (PBE1PBE) calculations.

Although TDDFT calculations are known to overestimate the CT properties,⁴³ the better match to the experimental dipole moment difference experiment compared to MNDOCI calculations appears to originate in the identity of the primary charge donator and acceptor, and therefore the distance over which charge is transferred, rather than the magnitude of charge that is shifted on photon absorption. Therefore, a net charge shift toward the oxygen atom of the carbonyl group, and not away from it as suggested by MNDOCI calculations (Figure 6), could account for the large change in dipole moment measured here. In contrast to the TD-DFT calculations, MNDO- and SAC-CI calculations do predict the correct ordering of states and increasing correlation does lead to an increasingly larger dipole moment for the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state upon excitation. Therefore, the difference between experiment and theoretical estimations of the properties for the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state is likely not due to a failure of MNDOCI theory, but that the dipolar properties of the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state need to be interpreted in conjuction with that for the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state (discussed further below) where the electronic properties of the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like and the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like states are expected to be modulated by the solvent environment.

Another measure of coupling between energetically nearby electronic states can be obtained from the change in electronic polarizability, where strong coupling between S₂ and S₁ may be manifested as a very small or even negative ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{el}}$.^29,60,61 Indeed the experimental parameter ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$ is negative. However, the magnitude is too large (−680 ų) to be physically realistic, even if $\overline{\mathrm{\Delta }{\mathrm{\alpha }}_{\mathrm{e}}}<\overline{\mathrm{\Delta }{\mathrm{\alpha }}_{\mathrm{g}}}$, which strongly suggests that the transition moment polarizability term (A_ij) contributes to ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$ (eq 5). A_ij cannot be estimated from the current setup and method of analysis, unless the transition-moment hyperpolarizability (B_ijj) is presumed negligible (eq 2). The a_54.7 term (eq 2) is however large and negative, suggesting that A_ij could also be negative and the likely source of the large and physically unrealistic values for ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$ (Table 1). The decrease in A_ij, and the oscillator strength, in the presence of the external field could be similar to the decrease the oscillator strength of the closely related retinal with increasing solvent refractive index.⁶² A description to evaluate A_ij and ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{el}}$ are provided in ref 30 for a two-level system, but would be hazardous to apply to a system such as fucoxanthin where the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state is mixed with the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state.⁶³ However, ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$ cannot be used beyond this point to derive a useful physical description of Fx and will not be discussed any further.

Impact and Origin of the Large Dipole Moment of S₂

Transient absorption (TA) studies of other carbonyl-containing carotenoids, including Fx, elucidated, and drew attention to, their polarity-dependent dynamics that led to the identification of a distinct ICT state in all of them.^14,64,65 In FCP, this ICT state of Fx was shown to transfer energy with more than 90% efficiency to Chl-a.⁸ Thus far, much of the dynamics and polarity-dependent changes observed for Fx, and other carbonyl-containing carotenoids, has been attributed to the CT character of the ground-state and of the S₁/ICT state, whereas that of the S₂ state has been considered negligible and has not been taken into consideration when discussing the excited-state reactivity of these carotenoids.¹⁴ However, up to 40% of ET in FCP is achieved from S₂ directly to Chl-a,⁸ which is even more than in PCP.¹¹ Note that although |Δμ⃗|_exp of Fx is ~6 D smaller than that of peridinin, the μ_g of peridinin is ~5 D smaller than Fx.³⁸ The role of the S₂ state is often not discussed because of its rather short excited-state lifetime and weak solvatochromic response. However, the |Δμ⃗|_exp value of 17 D found for Fx clearly attests to the polar nature of the Franck–Condon region of the S₂ state produced on photon absorption, and should have a profound effect on the excited-state reactivity of Fx.

Calculations provide additional information about the nature of the Franck–Condon region of the excited states of Fx, but a direct comparison to the experimental results would need to take into account the effect of the solvent reaction field on the calculated dipolar properties of Fx that are obtained under vacuum conditions. Here, MNDO calculations consistently find the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state to have a (much) larger dipole moment than the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state. However, the mixing between these “covalent” and “ionic” states is so great that it is difficult to present an argument based on configurational interactions to explain why the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state has a larger dipole moment than the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state. In fact, increase in correlation (MNDOCI+ calculations in Table 4) results in lowering the energy of the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state accompanied by a loss in oscillator strength and ionic character being transferred to the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state to produce a dipole moment larger than in the ground state (Table 4).

The $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like and $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like states are actually of the same symmetry, or more precisely, C₁ (no symmetry). The C_2h-like symmetry labels that we use are only applicable to linear polyenes, and in polar, asymmetric polyenes such as Fx (μ_g ≈ 9 D), all the excited states are extensively mixed and will vary as a function of the solvent environment. Although MNDO-PSDCI calculations indicate that the covalent $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state possesses considerable “ionic” character, the solvent environment significantly affects the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state with increasing solvent polarizability (refractive index) at rt⁶⁶ and on glass formation (Table 1), indicating that the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state also possesses typical “ionic” character. Furthermore, mixing of the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like and $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like states is manifested in the two-photon fluorescence excitation spectra of Fx,⁶⁴ and supports the suggestion that experimental results for the dipolar properties likely reflect the effects of mixing between these two states.

A rough estimate for the mixing between the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like and $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like states may be discerned from the solvation of the ground-state dipole moment. Note that for an electronic transition in the condensed phase, the solvent field arising from both the orientational and electronic polarization is equilibrated with the ground-state dipole moment and polarizability. Whereas, in the Franck–Condon region only the electronic polarization component, arising from the high-frequency dielectric, is able to follow the change in the electronic charge distribution to equilibrate with the excited-state dipole moment and polarizability. At 77 K, MeTHF is estimated to have a reaction field of ~2.5 × 10⁷ volts/cm (∊₀ ≈ 19 and a refractive index of ~1.7). The large xx component in the polarizability tensor indicates that interaction with the solvent field would produce an induced dipole moment aligned primarily along the x-direction. The dipole moment enhancement, resulting from interaction of the solvent reaction field with the polarizability of the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state (~400 ų) of Fx, is estimated to enhance the dipole moment difference by ~5 D, along the same axis as the ground-state dipole moment,⁶⁷ with the proviso that the orientations of the induced dipoles, relative to the external field, are randomized. ⁶⁸ Thus, even though a small (static) dipole moment is calculated, it is obtained under vacuum conditions and is not necessarily representative of the dipole moment measured in the presence of the solvent reaction field.

In addition to the information to being able to compare the experimental and theoretical predictions for the dipolar properties of the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state, calculations also shed light on the origin of the heterogeneity in the Stark signal of Fx at the red edge (>20000 cm⁻¹). Most of the theoretical calculations are in general agreement on one aspect of the Fx excited-state properties, in that the lowest-lying excited singlet state carries the largest change in dipole moment. The somewhat larger change in dipole moment estimated for the red edge band (Table 1) could be attributed to contributions from the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state, which lies below the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state, but yet has sufficient oscillator strength to contribute to the observed Stark shift. Analysis of the λ_max band (Figure 5), in terms of log-normal vibronic bands, indicates the presence of a low-energy band (f_osc = 0.1376) that does not fit a normal vibronic progression. We suggest that this band may be associated with the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state. One way to better probe the differences between the red edge and the main manifold would be from transient absorption spectra generated using multiple excitation wavelengths.

The anomalous CT properties at the red edge of the absorption are also reflected in the solvatochromic effect of Fx. The shift of the 0–0 band differs, with increasing solvent polarity (∊₀), clearly differs from that of the 0–1 band (Table 6). In fact, the 0–0 band exhibits a solvatochromism opposite to that of the 0–1 band, which could be an indication that mixing with the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state affects the electronic properties of the 0–0 band. In fact the blue shift of the absorption maximum of Fx in acetonitrile to that in a less polar solvent, such as MeTHF, might suggests that μ_e < μ_g. However, comparing the absorption maximum in MeTHF relative to n-hexane, or in MeTHF at 77 K versus at rt, where the solvent refractive index and/or static dielectric constant (∊₀) increase, the red shift of the absorption maximum is consistent with μ_e > μ_g. The calculated solvent shifts indicate that a 5–10 D Δμ could account for the experimentally observed values (Table 6). Broadly, one may suggest that the larger solvent shifts predicted for the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state, which are closer to the experimental results for the absorption maximum, could indicate borrowing of CT character from the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state by the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state.

On the basis of the results from calculations and the results from Stark experiment, the identity of the ICT state depends on the description of the S₁ and S₂ states and on which one of these states is identified to intrinsically carry CT character. MNDOCI calculations indicate that it is the S₁ state that is polar, and that S₂ borrows CT character from S₁. Presumably, increased mixing occurs in more polar solvents. However, this results in the contradictory picture, both in theory (Supporting Information) and in experiment,¹⁴ of an increased energy gap between S₁ and S₂. If S₂ gains CT character due to mixing with S₁, the local field of the solvent (or protein) environment would certainly be implicated in this process. As recently discussed for noncarbonyl containing carotenoids, coupling between these two states could also be promoted by distortions along the single bonds of the polyene backbone.⁵ Alternatively, the S₂ state could be the one that intrinsically possesses CT character, as suggested by the typical ”ionic” and ”covalent” characteristics predicted by TD-DFT calculations for the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}-\text{and}{2}^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like states, respectively. Furthermore, the sub-100 fs decay of S₂ into ICT does not rule out the possibility that the ICT state corresponds to a vibronic level of S₂, which may intrinsically possess the CT properties characteristic of the ICT state, or instead may be strongly coupled to S₁ to produce the S₁/ICT state.

The Electronic Properties of the Fucoxanthins in FCP

Early investigations on the energy-transfer pathways of the carotenoids in FCPA complexes, isolated from the brown alga D. dichotoma, led to the finding by Mimura et al.⁴ that ET to Chl-a did not primarily occur from the S₂ state as it does in its noncarbonyl containing counterpart, neoxanthin.^7,69 Implicitly implicated in the efficient light harvesting and ET efficiencies of Fx, as well as of peridinin and siphonaxanthin, is the carbonyl group conjugated to the polyene backbone.¹⁴ The results from the Stark spectrum of Fx, discussed above, further support this proposition, and underpin the functionality of the Fx’s in FCP.

In FCP, two distinct populations of Fx’s, Fx_blue and Fx_red, are identified from the fit to the absorption spectrum at rt to be present in nearly equal amounts. Their energetic locations reflect their distinctly different conformations and/or local environments, with Fx_red being better solvated and stabilized than Fx_blue. (Red shifts can generally be accounted for by an increase in polarity of the environment and/or closer electrostatic interaction with adjacent molecules, which is strongly dependent on the dipolar properties of the solute and solvent.) Indeed, the pronounced charge-transfer character of Fx_red is evident in the ~40 D |Δμ⃗|_exp of band I (Figure 3b), which is significantly larger than that estimated for the red-edge absorption of the carotenoid lutein, which lacks a carbonyl group, in LHCII.³² Note that both here and elsewhere, the Stark-spectrum analysis of these red-absorbing carotenoids is derived for a red-edge band that more closely approximates the width of a vibronic (likely the 0–0 band) rather than an electronic transition, and should be interpreted as such. The lower absorption maxima of Fx_red suggests that these Fx’s have longer conjugation lengths, which is by the relatively lower Raman frequency of the C=C stretch (unpublished), which could act like a molecular wire to shift charge over a longer distance than in Fx_blue, which could thus account for its much smaller change in dipole moment.

Strong Coulombic coupling between the S₂ state of Fx and Chl-a would be promoted by the large excited-state dipole moment (55 D) of these red Fx’s and could explain the ultrafast ET to Chl-a,⁸ before internal conversion to the S₁/ICT state. Indeed in this short time window, up to 40% of the absorbed energy is transferred to Chl-a, which supports the picture of strong coupling between the S₂ state of Fx and Chl-a. (The large |Δμ⃗|_exp (~40 D) indicates that the Fx_red’s are very polarizable in the excited-state and the induced dipole moment, which is directly related to the transition dipole moment expressed in the Förster energy transfer formula.¹²) Also to be considered is the solvating effect of nearby pigments, amino acid residues of the trans-membrane polypeptide, or even water molecules.⁷⁰ Here, for example, the local field in the proximity of a Chl-a, with a ground-state dipole moment of about 5 D,⁷¹ would be on the order of 3 × 10⁶ V/cm (similar to hexane) at a distance of 10 Å, and 2 orders of magnitude larger, 4 × 10⁸ V/cm (similar to acetonitrile), when it is 2 Å away. These values are estimated using the simple approximation of 2 μ/r³ for a spherical cavity.³³ Note that specific alignment, as in LHCII,³ could result in π-stacking between the porphyrin ring of Chl-a/c₂ and the polyene backbone of Fx to more strongly couple the two systems. The orientation of the adjacent molecule could provide a directing field that promotes charge transfer toward the carbonyl group and increase ET efficiency.

Another impact of the large |Δμ⃗| of Fx_red can be seen in two-photon spectra in which the type II process is active.³⁸ The two-photon fluorescence spectrum of a Fx-containing thylakoid, from the diatom P. tricornutum,⁶⁴ is quite similar to that of PCP³⁸ in that there is strong overlap between the two-photon fluorescence excitation and the single-photon absorption profiles. The type II process is manifested if the one-photon allowed state has a large dipole. In fact, the |Δμ⃗|_exp measured for band I (Fx_red) in FCP is a factor of 2 larger than that measured for Fx in MeTHF, implying up to 0.85 units, transferred over 10 Å, and would suggest even stronger coupling between S₂ and S₁ (or S₁/ICT) state in the protein environment to promote internal conversion (IC) to transfer the remaining 60% of absorbed energy to Chl-a.⁸ Increased coupling between the S₁/ICT and S₂ states could account for the substantially larger |Δμ⃗|_exp of band I, where S₂ borrows CT character from the S₁ state more efficiently than in solution. A small geometry distortion of Fx_red or, binding-site induced field effects could enhance coupling between the S₂ and ICT states. The properties of band I in FCP are not only comparable to LHCs containing peridinin, but also to the LHCs of green algae containing siphonaxanthin.¹³ In fact, the dynamics and transient-absorption spectra of Fx more closely resemble that of siphonaxanthin, than of peridinin.¹⁴

In contrast to Fx_red, the higher-energy Fx’s, whose properties are best simulated by band III (Figure 3a), appear to have significantly smaller CT properties. In Fit-FCP_A, band IIIA approximately corresponds to the 0–0 and 0–1 bands of Fx_blue, and the |Δμ⃗|_exp value obtained is about one-third of the 15 D value estimated for Fx in MeTHF. Although this |Δμ⃗|_exp may be indicative of Fx_blue being in a less polar site than in MeTHF, band IIIA is in an energetic region that is strongly overlapped with that of Chl-c₂ (Figure 3a). The attenuation of the Stark signal in this region and the electrostatic properties derived for band IIIA may thus correspond to the Soret band of Chl-c₂ rather than to Fx_blue. In Fit-FCP_B, band IIIB has minimal overlap with Chl-c₂ and only comprises the 0–0 band of Fx_blue and in this case, the change in dipole moment is similar to that of Fx in MeTHF (Table 1). If indeed band IIIB is more representative of Fx_blue than band IIIA, such a dipole moment change, albeit much smaller than in the Fx_red’s, would continue to aid ET from the Fx_blue’s to Chl-a, or possibly to the Fx_red’s.

Steady-state spectroscopy studies on FCP complexes from C. meneghiniana showed that Fx and Chl-c₂ independently transferred energy to Chl-a,^8,19 similar to that observed long ago in FCP complexes from D. dichotoma.⁴ However, the Fx_blue’s could also transfer their absorbed energy to the Fx’s lower in the energy scaffold. In fact, circular dichroism (CD) spectra show evidence for (strong) excitonic interaction between 430–500 nm, which was previously attributed to the interaction between Fx and Chl-a,¹⁹ but could actually be indicative of ET among the blue Fx’s. The maximum positive signal at +440 nm, with a shoulder at +412 nm, could well correspond to the 0–1 and 0–2 bands of a blue Fx (ΔE ≈ 1400 cm⁻¹), which appears to be distinct from the Fx_blue used in the fits both at rt and at 77 K. Although the minimum of the CD band is at −476 nm, the presence of the shoulder at −465 nm suggests that the maximum of the other Fx may be the Fx_blue modeled here. Furthermore, the intensity of the CD signal is related to the sine of the angle between the transition dipole moments of the two interacting molecules and suggests that the polyene backbones of these two Fx’s are far from parallel to each other. These two blue Fx’s are likely bound in the FCP complex similar to the two luteins in LHCII: next to the two α-helices that form a cross-brace and are conserved in FCP.³ Like the two luteins, these two Fx’s could serve to provide stability to the complexes, as well be involved in photoprotection.⁷² Furthermore, increased excitonic interaction between these two Fx’s could result in a diminution of their static dipole moments and explain the weak Stark signals seen in the region of Fx_blue absorption.

In addition to Fx_red and Fx_blue, there appears to be a third Fx, modeled by band II, which is situated in the region of overlap between these Fx’s. Band II exhibits properties distinct from those of bands I and III; summing band II with band I, or alternatively with band III, resulted in very poor fits in these energetic regions. A good fit to the Stark spectrum was obtained only when bands I, II, and III were deconvolved and fit separately. This suggests that between 18500 and 21000 cm⁻¹, bands I, II, and III (or gaussians 2, 3, and 4), each contain contributions from pigments with distinctly different electrostatic properties. Note that in the fit to the absorption of FCP, the modeled Fx absorptions takes into account only 2 out of 4 Fx’s. The uniqueness of band II could thus be indicative of the presence of a third Fx, distinct from Fx_red and Fx_blue.

Modeling Fx’s in the Stark Signal of FCP

To determine whether more than two different types of Fx’s could contribute to the Stark signal measured for FCP, we tried to reproduce the Stark signal of FCP in Figure 4 by appropriately shifting and scaling the Stark signal of Fx in MeTHF. Using Fx_red and Fx_blue as a starting point, the Stark spectrum of Fx in MeTHF was shifted by −1500 and +300 cm⁻¹ (Fx-2 and Fx-4, respectively, in Figure 4) and attenuated according to the absorption intensities (not shown). The sum of Fx-1 and Fx-4 very poorly reproduce the Stark signal, and two additional Fx Stark spectra, shifted by −1750 cm⁻¹ (Fx-1), and by +1000 cm⁻¹ (Fx-3), were included to produce a reasonable approximation of the Stark signal of FCP (compare dark dot-dash and solid lines in Figure 4). In this fit, the two red-most Fx’s, Fx_red1 and Fx_red2, cannot be definitively stated to be electronically different as spectral broadening has not been taken into account. Note that an increase in polarity not only red shifts an absorption spectrum, if μ_e > μ_g, but also leads to greater inhomogeneous broadening and loss of structure.⁷³ The absorptions of Fx-1 and Fx-2 (Figure 4), may thus correspond to the broadened absorption of a single Fx_red. Importantly, the inclusion of band II in the fit to the Stark spectrum appears to be justified based on the need to include Fx-3 (Fx_green) in modeling the Stark signal in this region. There is a small possibility that this Fx_green, which lies between Fx_red and Fx_blue, may be the one that is excitonically coupled to Fx_blue (see discussion above) to yield the large CD signal. Additionally, if the origin of the large CD signal is due to two different Fx_blue’s, then one must consider the possibility that there are more than four Fx’s per polypeptide in FCP.

The fit to the Stark signal (Figure 4) and the dipolar properties derived by using different combinations of bands to fit the Stark spectrum of FCP suggests the presence of at least three, if not four, electrostatically distinct Fx’s that may be found in nonidentical sites and/or conformations in FCP. These differences among the Fx’s, notably their different absorptions and electrostatic properties, reflect the extent to which the protein environment fine-tunes the properties of Fx to best harness its potential for light harvesting. A case in point is the absorption of the Fx_red’s, which are more than 1500–2000 cm⁻¹ below that of Fx in the MeTHF glass, suggesting that their local environment may have an effective refractive index >1.75. However, as the solvent shift analysis showed, it is not only the polarizability (refractive index) of the environment, but also the static dielectric constant, that is, the polarity of the environment that has a significant effect on the absorption maximum. Given the large ground- and excited-state dipole moments of Fx, this result is not surprising. A rough estimate for the refractive index and ∊₀ of the local environment of the Fx_red’s may be made from the solvent shift that would arise using our calculated and experimental results for the dipole moments and polarizabilities. However, with a refractive index of 1.5,⁷⁰ or even 1.75 as in a MeTHF glass, and an ∊₀ of 35, as in acetonitrile, only a 600 cm⁻¹ shift relative to hexane is obtained, using a μ_g of 9 D and μ_e = 50 D. The only way to account for the 3000 cm⁻¹ shift in energy of the Fx_red’s relative to Fx in hexane, would be to shrink the solute cavity. A decrease of 6 Å along the x-axis of the ellipsoidal cavity would produce such a shift. However, even if the Fx’s were somewhat distorted beyond the polyene backbone, which must presumably maintain an all-trans geometry, it should not shrink the length along the x direction by more than 1–2 Å and there is no obvious justification for reducing the cavity size by up to 6 Å. The red shift of the Fx’s in the protein cavity must thus arise from additional environmental effects. For example, the protein environment could control the magnitudes of the dipole moments by the location and alignment of polar side groups next to Fx in a way that stabilizes the polyene backbone, and perhaps more importantly, to shift charge toward the carbonyl oxygen on photon absorption.

Electronic Properties of Chlorophylls in FCP

The fit to the Chl-a Q_y band is quite good, because the narrow absorption band generates a large Stark signal and provides a precise measure of the dipolar properties. A change in dipole moment of only 0.92 D measured here for the Q_y band of Chl-a, is somewhat larger than the 0.6 D found in some LHCIIb samples³² and more similar to others.⁷⁴ These differences between these results are however too small to be significant, within the error margins, regarding the magnitude of charge transfer implied by these|Δμ⃗|_exp’s. The value of 0.92 D constitutes ~0.2 unit of charge moving over 1 Å on photon absorption. For the Q_y transition of Chl-a, charge transfer from magnesium to the C9 carbonyl oxygen, over ~7 Å, would suggest only a 0.03 unit of charge motion. The ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$ value of 20 ų for Chl-a, in FCP, is half-that measured in LHCIIb,³² and indicates that the excitation of Chl-a is unlikely to be delocalized beyond a single Chl-a molecule, if the electronic polarizability is qualitatively visualized as the volume of the electron density over which the excitation may be (de)localized. Delocalization of excitation over another chlorophyll molecule should be on the order of their molecular volumes. The localized nature of Chl-a that is suggested here is in agreement with that determined for “monomeric” Chl-a in LHCII.⁷⁴ The slight asymmetry in the fit at red edge (14500–14800 cm⁻¹) suggests the presence of another electronically distinct Chl-a, whose electrostatic properties should be on the same order of magnitude as that of the bulk of the Chl-a’s that absorb at higher energy. The rather small dipole moment of Chl-a highlights the importance of the large dipole moment possessed by Fx to bring about efficient ET.

The electrostatic properties of the Soret band of the chlorophylls, and in particular Chl-c₂, may be best discerned from band IVB, although this band also contains a significant contribution from Fx (see Figure 3a: 21000–24000 cm⁻¹). The difference dipole moment of ~4 D obtained, if assigned purely to the Soret transition of Chl-c₂, is rather small compared to Fx. This value suggests that the nearly perfect efficiency of ET from Chl-c₂ and Chl-a must be aided by the close proximity of the two molecules. A future publication will explore the structural differences of the Chl’s in greater detail using Raman spectroscopy.

Conclusions

The electrostatic properties of fucoxanthin have been determined in MeTHF at 77 K, and show that excitation from S₀ → S₂ $(1^1{\mathrm{A}}_{\mathrm{g}}^{-}-\text{like}\to 1^1{\mathrm{B}}_{\mathrm{u}}^{*+}-\text{like})$ produces a 17 D |Δμ⃗|_exp. Fucoxanthin thus undergoes photoinduced charge transfer, suggesting that the interaction between the initially excited-state and the S₁/ICT states would be affected by the large dipole moment of the S₂ state (ca. 25–27 D). Furthermore, red-edge excitation of Fx (>19000 cm⁻¹) results in a larger |Δμ⃗|_exp (>22 D), which could provide a faster channel for ET. Given that the angle between |Δμ⃗|_exp and the transition dipole moment is the same (20°) for both these states, they originate from a species with the same molecular geometry. The Δμ value from TD-DFT (PBE1PBE or B3LYP) calculations are in agreement with experiment and suggest an overall shift in charge from the allene end of the polyene backbone toward the carbonyl oxygen upon excitation into the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state. MNDOCI calculations, which correctly predict the energetic ordering of the states, yield a small dipole moment change for the S₀ → S₂ transition. Although large CT character was not evident for the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state from MNDOCI calculations, a complex interaction with the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state, for which a large dipole moment is calculated, is suggested because increasing correlation not only increases the energy gap between these states, but also results in CT character being transferred to the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state. The solvent or protein environment is thus expected to significantly couple these two states such that the $1^1{\mathrm{B}}_{\mathrm{u}}^{*+}$-like state “inherits” the CT character of the $2^1{\mathrm{A}}_{\mathrm{g}}^{*-}$-like state to allow it to accomplish ET from the S₂ state to Chl-a in FCP.

In FCP, three Fx’s species possessing distinct electrostatic properties are identified, with a broad distinction between two populations, the red-absorbing Fx_red’s and the higher-energy Fx_blues’s. The Fx_red’s are distinguished by their |Δμ⃗|_exp values on the order of 40 D, which are a factor of 2–4 larger than of the Fx_blue’s. Such a large change in dipole moment is expected to play an important role in inducing strong coupling of Fx_red to Chl-a, via Coulombic interactions, and promote ET directly from the S₂ state of Fx. In contrast, the Fx_blue’s, that are less efficient at ET to Chl-a, have much smaller |Δμ⃗|_exp’s and may be involved in transferring their absorbed energy to Fx_red. Overall, the electrostatic properties uncovered for the S₂ state of Fx, both in solution and at different (energetic) locations in FCP, underscore the role of the S₂ state in initiating the cascade of ET events to Chl-a. The |Δμ⃗|_exp of 0.92 D, and ${\overline{\mathrm{\Delta }\mathrm{\alpha }}}_{\text{exp}}$ of 20 ų, determined for the Q_y band, attests to the monomeric nature of Chl-a in the FCP complexes and further demonstrates that much of the coupling strength between Fx and Chl-a is likely provided by Fx. The Soret absorption band of Chl-c₂ also appears to have a relatively small change in dipole moment (2–4 D) and suggests that ET to Chl-a, from Chl-c₂, should be assisted by the close proximity of the chlorophylls.