Mapping the dynamics of ligand reorganization via ¹³CH₃ and ¹³CH₂ relaxation dispersion at natural abundance

Abstract

Flexible ligands pose challenges to standard structure-activity studies since they frequently reorganize their conformations upon protein binding and catalysis. Here, we demonstrate the utility of side chain ¹³C relaxation dispersion measurements to identify and quantify the conformational dynamics that drive this reorganization. The dispersion measurements probe methylene ¹³CH₂ and methyl ¹³CH₃ groups; the latter are highly prevalent side chain moieties in known drugs. Combining these side chain studies with existing backbone dispersion studies enables a comprehensive investigation of µs–ms conformational dynamics related to binding and catalysis. We perform these measurements at natural ¹³C abundance, in congruence with common pharmaceutical research settings. We illustrate these methods through a study of the interaction of a phosphopeptide ligand with the peptidyl-prolyl isomerase, Pin1. The results illuminate the side-chain moieties that undergo conformational readjustments upon complex formation. In particular, we find evidence that multiple exchange processes influence the side chain dispersion profiles. Collectively, our studies illustrate how side-chain relaxation dispersion can shed light on ligand conformational transitions required for activity, and thereby suggest strategies for its optimization.

Introduction

In drug discovery, traditional structure-activity-relationship (SAR) investigations search for correlations between ligand structure and biological activity to drive ligand optimization. But such investigations can become complicated if the ligand can adopt more than one structure—that is, when the ligand is flexible. In such cases, the relationship between structure and activity can become ambiguous.

This ambiguity is a genuine concern in drug design: one often encounters flexible ligands in the course of lead generation and iterative optimization. Such ligands may be chemical probes used to extract functional information, or lead compounds under the process of optimization. Flexible ligands are also prominent in current drugs. Examples include peptido-mimetic compounds, such as Telaprevir, a current Phase III clinical candidate for HCV protease (Perni et al. 2007), as well as HIV-1 protease inhibitors (King et al. 2004). These ligands retain a number of rotatable bonds, whose torsion angle mobility allows for conformational readjustments upon protein binding. Indeed, an analysis of 150 crystal structures of flexible drug-like molecules bound to their protein targets by Perola and Charifson show that the bound ligand conformations often do not correspond to the calculated conformational energy minima of the free ligand (Perola and Charifson 2004). This means flexible ligands frequently undergo conformational reorganization upon binding. Such re-organization can lead to confounding or non-intuitive SAR.

To optimize the binding properties of flexible ligands, it would be useful to have methods that can describe in a site-specific manner where and how the ligand reorganizes upon complex formation. Such methods could illuminate which degrees of freedom come into play, what their relative amplitudes of motion are, and how they transform the free ligand conformational ensemble into the presumably narrower bound ligand ensemble. The resulting information could help estimate the reduction in the accessible ligand conformational space caused by binding, and provide insight into the ligand conformational entropy changes.

Accordingly, we have approached the problem of characterizing ligand conformational reorganization by exploiting the well-known power of NMR nuclear spin relaxation measurements to profile molecular dynamics. In particular, we have used ¹³C relaxation measurements to profile the internal flexibility of ligands in their free versus protein-complexed states. ¹³C relaxation parameters are appealing because they can be interpreted in a site-specific manner, and carbons are prevalent in drug-like molecules. Previously, we demonstrated methods to probe faster ps-ns motions of aromatic ¹³C methine (CH) nuclei, using natural abundance exchange-transferred cross-correlated relaxation (Peng 2003). More recently, we demonstrated the utility of natural abundance ¹³C Carr-Purcell-Meiboom-Gill (CPMG) relaxation dispersion measurements to probe the slower µs-ms exchange-dynamics of methine (CH) ¹³Cα nuclei in peptide ligands upon protein binding (Zintsmaster et al. 2008).

Here, we look beyond the methine CH moiety to the methyl CH₃ and methylene CH₂ moieties. A retrospective study of the comprehensive medicinal chemistry (CMC) database by Bemis and Murcko show that CH₃ moieties are among the most common side chains in drug-like molecules (Bemis and Murcko 1999). Methylene CH₂ groups may be part of linkers or non-aromatic ring structures (Bemis and Murcko 1996). The prevalence of these moieties makes them worthy probes of ligand flexibility for molecules of pharmaceutical interest.

We demonstrate here the ability for natural abundance ¹³C dispersion measurements of side-chain CH₃ and CH₂ groups to illuminate the µs-ms conformational transitions required of the ligand for biological activity. This entails ¹³C relaxation dispersion studies of the interaction between the 18.4 kDa peptidyl-prolyl isomerase, Pin1, and a 10-residue phosphopeptide ligand that contains the target sequence from the Pin1 substrate, Cdc25 phosphatase. As with our previous studies, we work at natural ¹³C abundance (> 1%). While the dispersion methods are, of course, applicable to isotope-enriched ligands, such ligands are uncommon in pharmaceutical research settings, due to considerations of cost and synthetic complexity. Hence, it is important to demonstrate the feasibility of these dispersion experiments at ¹³C natural abundance. Historically, natural abundance measurements required ultra-high ligand concentrations (>10 mM). Fortunately, the availability of high magnetic fields and cryogenically-cooled probes have reduced these requirements to 1–2 mM. A notable side-benefit of natural abundance ¹³C is that homonuclear ¹³C–¹³C dipolar and scalar couplings, which can complicate relaxation measurements, are effectively eliminated.

Under ideal conditions, ¹³C dispersion experiments can provide the ¹³C chemical shift changes associated with complex formation. ¹³C chemical shifts are widely recognized as probes of local conformation (Cornilescu et al. 1999; de Dios et al. 1993; Spera and Bax 1991; Wishart and Sykes 1994; Xu and Case 2002) and there is now intense interest in chemical shifts as the principal drivers of overall protein conformation (Cavalli et al. 2007; Shen et al. 2008) and conformational fluctuations (Berjanskii and Wishart 2006). In this context, the ¹³CH₃ and ¹³CH₂ dispersion studies disclosed here shed light on side-chain moieties that must undergo conformational readjustments upon complex formation. Our broader aim is to combine the ligand dynamics perspective gained from ligand ¹³C relaxation measurements (for both backbone and side chain), with the protein dynamics perspective gained from more widespread protein studies. Combining the ligand and protein perspectives should provide a more comprehensive database for learning how to cope with non-intuitive SAR caused by ligand and/or protein flexibility.

Our report proceeds as follows. After a description of material and methods, we describe the Pin1/ligand system. We then present the results of the relaxation dispersion measurements for both ¹³CH₃ and ¹³CH₂ groups at two static field strengths and two temperatures. We discuss the extracted exchange parameters, and what they imply about complex formation. This includes follow-up studies involving a truncated construct of Pin1. We conclude with comments on the significance of these results in terms of a methodology for describing ligand conformational reorganization.

Materials and methods

Samples

NMR samples consisted of a 10-residue phosphopeptide ligand in the absence or presence of U-¹⁵N, 70%-²D human Pin1. The phosphopeptide, E1-Q2-P3-L4-pT5-P6-V7-T8-D9-L10 (purchased from QCB) contains the Pin1 pT-P target sequence from the mitotic phosphatase, Cdc25, a well-established Pin1 target (Crenshaw et al. 1998; Zhou et al. 2000).

U- ¹⁵N and 70% ²D Human Pin1 (1–163) and the truncated construct, Pin1-PPIase (40–163) were overexpressed in E coli strain BL21 (DE3) and purified chromatographically from the bacterial lysate. The truncated construct omits the first 39 residues corresponding to the WW domain (vide infra). U- ¹⁵N and 70% ²D enrichment was achieved by growing the cells in M9 media (90% D₂O) containing ¹⁵NH₄Cl as the sole nitrogen source. Details have been given elsewhere (Namanja et al. 2007). The 70% perdeuteration of the Pin1 aliphatic carbons reduces intermolecular proton dipolar relaxation losses that would otherwise compromise sensitivity, and further promotes selective ligand detection.

Samples containing Pin1 and the Cdc25 ligand consisted of 50 µM Pin1 and 2 mM Cdc25. Samples of the isolated ligand consisted of just 2 mM Cdc25. For all samples, the buffer conditions were 30 mM deutero-imidazole pH 6.6, 30 mM sodium chloride, 0.03% sodium azide, 1 mM deutero-dithiothreitol and 10% D₂O.

Correct folding of Pin1 was assessed from the ¹⁵N–¹H chemical shift dispersion in 2-D ¹⁵N-¹H TROSY-HSQC spectra. Pin1 isomerase activity was confirmed from 2-D ¹H-¹H EXSY exchange cross-peaks between ligand ¹H resonances corresponding to the trans and cis isomers. Integration of the 1-D ¹H resonances of the trans and cis resonances at 295 K indicated ~ 10% cis population.

NMR experiments

We recorded all spectra on Bruker Avance systems (16.4 T and 18.8 T) equipped with TCI cryoprobes. We used established proton-detected pulse schemes to measure ¹³C relaxation dispersion for both methyl ¹³CH₃ and methylene ¹³CH₂ carbons. For the methyl ¹³CH₃ experiments, we used the sequence by Lundström et al. (Lundström et al. 2007). For the ¹³CH₂ experiments, we used the sequence by Mulder et al. (Mulder et al. 2001b). Both experiments use the relaxation-compensated Carr-Purcell-Meiboom-Gill (CPMG) spin-locking (Carr and Purcell 1954; Meiboom and Gill 1958), originally developed by Loria et al. (Loria et al. 1999). The relaxation-compensated schemes remove the dependence of the transverse relaxation rate on the CPMG inter-pulse delay, t_cp, caused by oscillation between in-phase and antiphase coherences. The compensation thus assures that any variations in transverse relaxation rates with t_cp reflect bona fide chemical exchange.

The dispersion experiments produce 2-D ¹³C–¹H spectra in which the cross-peak intensity of each ¹³C nucleus is modulated by exp(−R_2effT_RELAX). R_2eff is a rate constant that describes the effective transverse relaxation during a CPMG spin-lock of fixed length, T_RELAX. For the dispersion studies, the key experimental parameter is the effective frequency of the CPMG spin-lock, ν_eff = 1/2t_cp. The dispersion studies consist of measuring a series of 2-D spectra that correspond to increasing ν_eff (decreasing t_cp). Analyses of the cross-peak intensities over the series produces for each ¹³C a R_2eff versus ν_eff profile. Those carbons with R_2eff versus ν_eff profiles displaying dispersion—a frequency dependence—are sites of chemical exchange, and are subjected to subsequent model-fitting for the extraction of site-specific exchange dynamics.

Generally, our dispersion studies included measurements at two static fields: 16.4T (700 MHz ¹H Larmor frequency) and 18.8T (800 MHz ¹H Larmor frequency). ¹³C hard pulses were applied at 17.86 kHz. The CPMG refocusing 180°s were applied at a lower strength of 6.7 kHz. In each dispersion series, we recorded duplicates of the reference spectra (spectra in which the CPMG is omitted) for subsequent uncertainty estimates.

¹³CH₃ methyl dispersion experiments were acquired with the ¹³C carrier centered at 17.4 ppm and a ¹³C sweep-width of 18.2 ppm. Unless the temperature is specified explicitly below, the same parameters were used at both 278 and 295 K. We generally acquired 32 scans per increment, and a total of 26 complex points, resulting in 1 h per 2-D spectrum. For Cdc25 in the presence of full-length Pin1, we used T_RELAX = 88.1 ms, and the ν_eff = 1/2t_cp values were as follows: 46, 92, 139, 187, 235, 284, 334, 385, 436, 487, and 540 Hz. For Cdc25 in the presence of Pin1-PPIase, we used a longer T_RELAX = 120 ms, with ν_eff = 34, 67, 102, 136, 171, 206, 242, 278, 314, 351, 426, 502, and 540 Hz. For the isolated ligand we took a smaller range of ν_eff samples, after observing no significant changes between the lowest and highest ν_eff values. At 278 K, 16.4 T, T_RELAX = 120 ms, and ν_eff values included 34, 67, 102, 136, 351, 426, and 540 Hz, while at 295 K, 16.4T, T_RELAX = 88.1 ms, and ν_eff values were 46, 92, 187, and 540 Hz.

For the ¹³CH₂ methylene dispersion experiments, the ¹³C carrier was centered at 48 ppm. For Cdc25 in the presence of full-length Pin1, we used T_RELAX = 40.0 ms, with ν_eff = 1/2t_cp values as follows: 50, 102, 153, 206, 260, 314, 369, 426, 483, and 540 Hz. At 16.4 T, 295 K we took 384 scans per increment (5.6 h per 2-D); in all other series we acquired 256 scans per increment (3.7 h per 2-D). In all cases, we collected a total of 14 complex points over a ¹³C sweep-width of 56.8 ppm. For Cdc25 in the presence of Pin1-PPIase, we used a longer T_RELAX = 64 ms, with ν_eff = 31, 63, 95, 127, 193, 328, 468, and 540 Hz. For the isolated Cdc25 ligand, we saw no significant intensity changes between the highest and lowest ν_eff values, and so used a smaller sampling of ν_eff values. At 278 K, 16.4T, we used T_RELAX = 40 ms with ν_eff = 50, 206, 314, 426, and 540 Hz. At 295 K, 16.4T, we used T_RELAX = 64 ms, with ν_eff = 31, 63, 95, 127, 193, 328, 468, and 540 Hz.

We also performed ¹H–¹H EXSY spectra to verify Pin1 isomerase activity on the Cdc25 phosphopeptide substrate. The exchange mixing time employed a continuous-wave spin-lock (as in ROESY), bracketed by 4 ms ¹H adiabatic rotations (Mulder et al. 1998). The spin-lock field strength was 2.0 kHz, and was centered on the methyl protons of pT5. These protons showed resolved ¹H resonances corresponding to the major trans and minor cis populations in 1-D spectra. Exchange mixing times (i.e. the entire time interval between the t₁ and t₂ chemical-shift evolution periods), included: 22, 31, 41, 61 (2×), 72 (2×), 81 (2×), 101, 121 (2×), 171, and 221 ms. Selective gradient-echo sandwiches (p90—gradient—sel-p180—gradient) prior to t₁ and t₂ allowed narrower spectral widths of 3.57 ppm in both dimension. The sel-p180 was an 8 ms REBURP pulse with a peak amplitude of 500 Hz (Geen and Freeman 1991).

Data reduction

All spectra were processed using Bruker Topspin 1.3 software. Subsequent measurement of cross-peak intensities, extraction of relaxation rates, and fitting of exchange parameters used in-house C-programs.

For resolved ¹³C–¹H cross-peaks, we obtained R_2eff versus ν_eff = 1/2t_cp profiles from the relation R_2eff(1/2t_cp) = −1/T_RELAX × ln{I(1/2t_cp)/I_ref} (Mulder et al. 2001a). I(1/2t_cp) and I_ref are the cross-peak intensities in the presence and absence of the CPMG spin-lock. Uncertainties in the rate constants were estimated by Monte Carlo simulations, based on spectral duplicates.

We fit the resulting R_2eff versus ν_eff profiles to the general two-state exchange model, using the Carver-Richards expressions (Carver and Richards 1972; Millet et al. 2000). The Carver-Richards expressions apply to all time scales of exchange, and consist of four adjustable parameters: the net exchange rate constant, k_ex; the fractional population of the minor species, p_B; the chemical shift difference between the two putative states, Δ_ppm; and R_2,0, the nominal non-exchange contributions to R_2eff, including relaxation caused by heteronuclear dipole-dipole interactions and anisotropic chemical shielding. To find the optimal parameters, we used in-house software to minimize the χ² error via a grid-search algorithm (Bevington 1969). For global fits, we kept k_ex and p_B the same for all ¹³C nuclei, while letting Δ_ppm and R_2,0 vary in a site-specific manner. Uncertainties in the resulting parameters were estimated by jack-knife simulations.

We obtained independent estimates of the exchange rate constants for cis-trans isomerization using aforementioned series of 2-D ¹H–¹H EXSY spectra. We fit the ratio of the exchange cross-peak intensity over the diagonal cross-peak intensity as a function of mixing time to the two-state EXSY expressions of Ernst et al. (Ernst et al. 1987) This yielded rate constants k_tc (trans to cis) and k_ct (cis to trans). From these rate constants, we obtained the net cis-trans isomerization rate constant k_ex,EXSY = k_tc + k_ct, which is the rate constant appropriate for comparison with k_ex extracted from ¹³C relaxation dispersion. Uncertainties in the rate constant were estimated via Monte Carlo simulations based on spectral duplicates.

Results and discussion

Our ¹³C dispersion experiments focus on the interaction of a ten-residue phosphopeptide, E1-Q2-P3-L4-pT5-P6-V7-T8-D9-L10, with the protein, Pin1. Pin1 is an 18.4 kDa peptidyl-prolyl isomerase that accelerates the cis-trans isomerization of phosphorylated-Threonine/Serine-Proline (pT/S-P) motifs in other cell signaling proteins (Lu et al. 2007). Pin1 has a modular design, consisting of a catalytic peptidyl-prolyl isomerase (PPIase) domain that is flexibly linked to a smaller WW domain. The PPIase domain is solely responsible for isomerase activity, while the WW domain functions as a docking module specific for pT/S-P motifs.

Our phosphopeptide ligand represents a pT-P motif from the mitotic phosphatase Cdc25, a well-known Pin1 target (Crenshaw et al. 1998; Zhou et al. 2000). Its Pin1 binding affinity is characterized by K_D = 8 ± 2 µM at 295 K (imidazole buffer pH 6.6). The K_D was determined by fitting Pin1 ¹⁵N–¹H chemical shift perturbations versus ligand concentration in the course of a ligand titration (Namanja 2009). Additionally, previous NMR studies of this phosphopeptide confirm the interaction of the pT5-P6 linkage with Pin1 (Namanja et al. 2007; Wintjens et al. 2001). Moreover, our own ¹H–¹H EXSY experiments show explicit cis-trans isomerization (vide infra). Thus, the Cdc25 phosphopeptide/Pin1 system is an illuminating choice for our dispersion studies, since we know at the outset that their mutual interaction perturbs the ligand conformational ensemble.

We measured ¹³C relaxation dispersion profiles, at natural ¹³C abundance ( ~ 1%), for methyl and methylene carbons of the Cdc25 ligand, using established 2-D ¹³C–¹H proton-detected pulse schemes. We examined the ligand in its isolated (free) state, and in the presence of Pin1. Samples containing both protein and ligand had a 40-fold molar excess of Cdc25 ligand (2 mM) over protein (50 µM). Since the total ligand concentration is much greater than K_D (8 ± 2 µM at 295 K, imidazole buffer, pH 6.6) we can safely neglect the free Pin1 concentration. The 40-fold ligand molar excess of ligand also serves to enhance the selective observation of ligand ¹³C resonances.

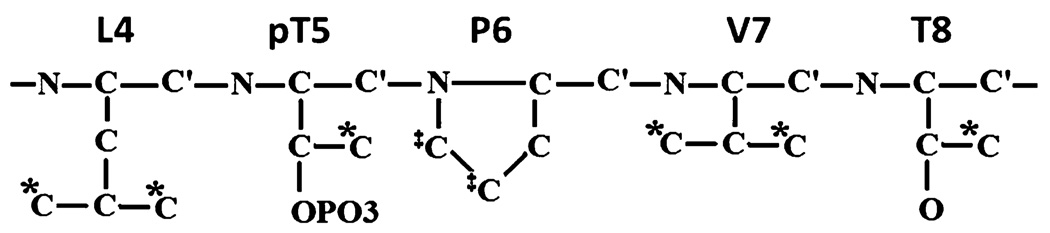
Figure 1 schematizes the five core residues of the Cdc25 ligand. The asterisks and double-daggers highlight the side-chain methyl and methylene carbons, respectively. Critically, methylene and methyl carbons bracket the isomerization epicenter—the pT5-P6 peptide linkage. Thus, it is reasonable to investigate the potential of these side-chain carbons as probes of µs-ms exchange dynamics via ¹³C relaxation dispersion measurements.

Fig. 1.

Schematic of the five core residues of Cdc25 phosphopeptide ligand, EQPLpTPVDL. Asterisks and daggers denote the methyl and methylene carbons highlighted in the ¹³C dispersion studies

Methyl dispersion measurements

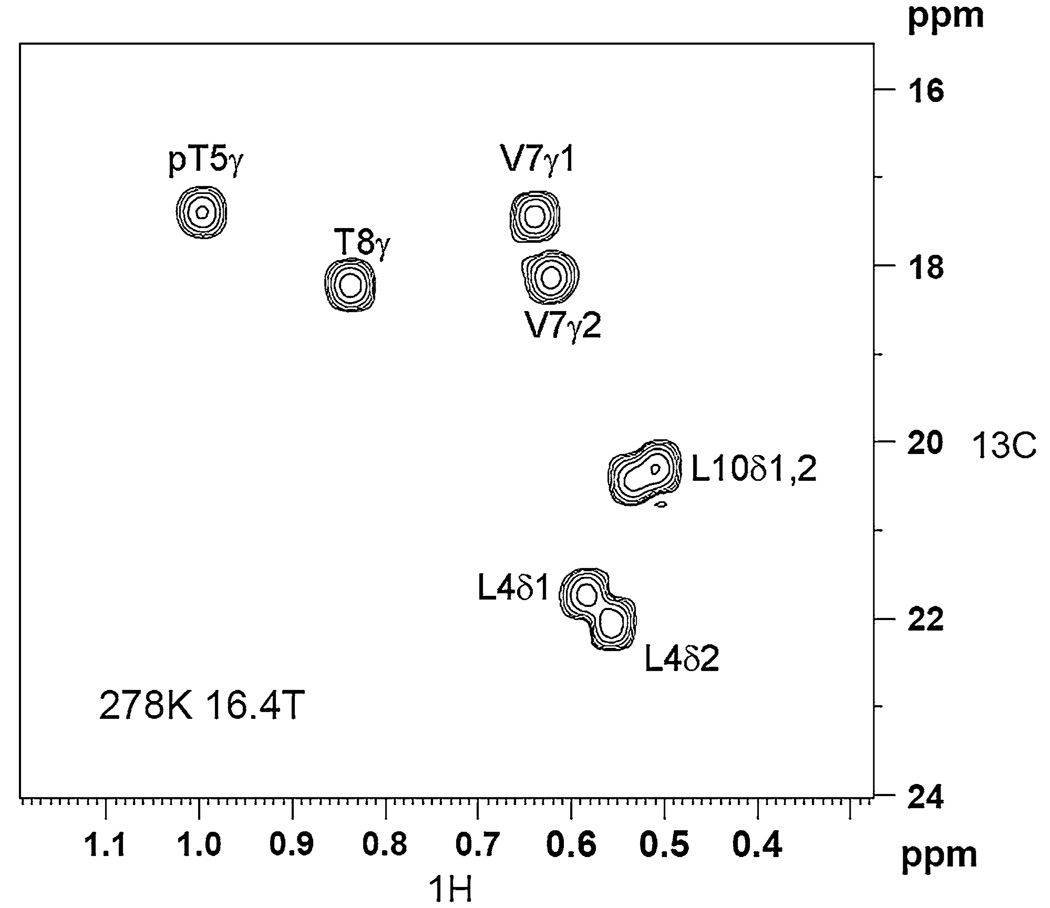
We used the 2-D ¹³C-¹H relaxation dispersion scheme of Lundström et al. (Lundström et al. 2007) for our studies of the Cdc25 ligand methyl carbons. Cdc25 ligand has eight methyl groups. Six of those eight give sufficiently resolved ¹³C–¹H cross-peaks in the corresponding dispersion spectra sufficient for analyses: L4-Cδ₁/δ₂, T5-Cγ, V7-Cγ₁/γ₂, and T8-Cγ. The Cδ methyl cross-peaks of L10 suffered severe overlap and were excluded from further analyses. Figure 2 shows an example spectrum of the Cdc25 methyls (in the presence of Pin1) at 16.4T (700 MHz ¹H Larmor frequency), with t_cp set to its longest value of 5.46 ms. The measurement time was 1 hr. We do not yet have stereospecific methyl carbon assignments, and so δ₁/δ₂ and γ₁/γ₂ simply indicate ¹³C–¹H cross-peaks that are downfield versus upfield along the ¹H chemical shift axis. For both the isolated ligand and the ligand in the presence of Pin1, we observe only one ¹³C–¹H cross-peak per methyl group.

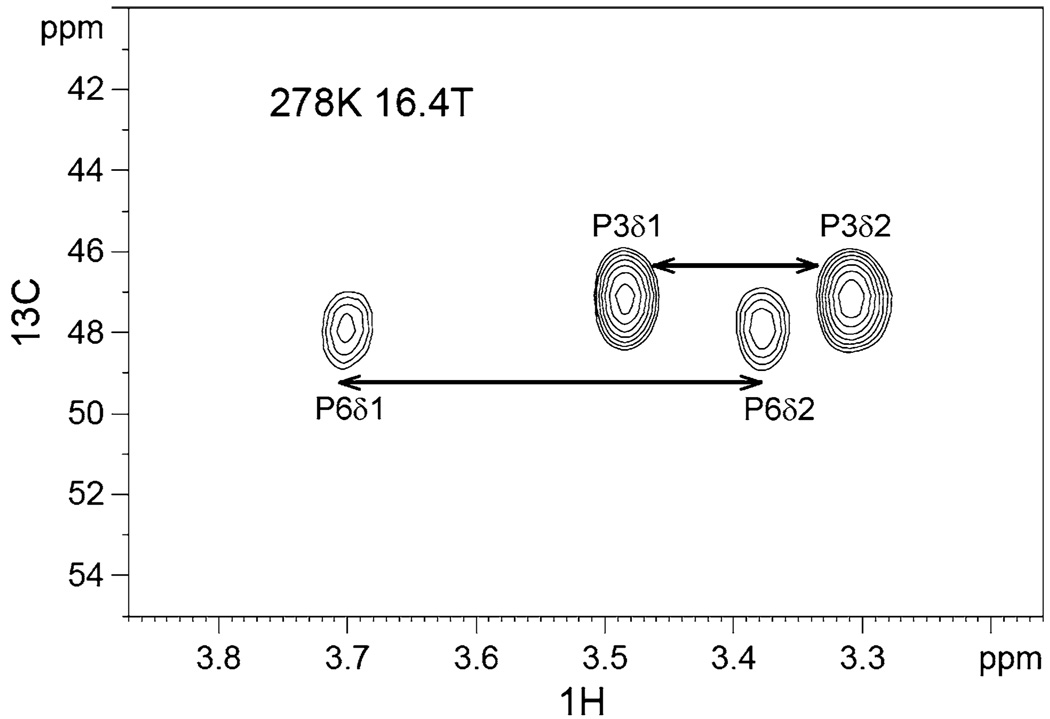
Fig. 2.

Example spectrum from the natural abundance ¹³CH₃ methyl dispersion measurements of the Cdc25 ligand (2 mM), in the presence of 50 µM U-¹⁵N/70%²D Pin1. The spectrum is recorded at 278 K, 16.4 T. The 2-D represents the lowest CPMG frequency ν_eff = 46 Hz. The total CPMG duration was 88 ms

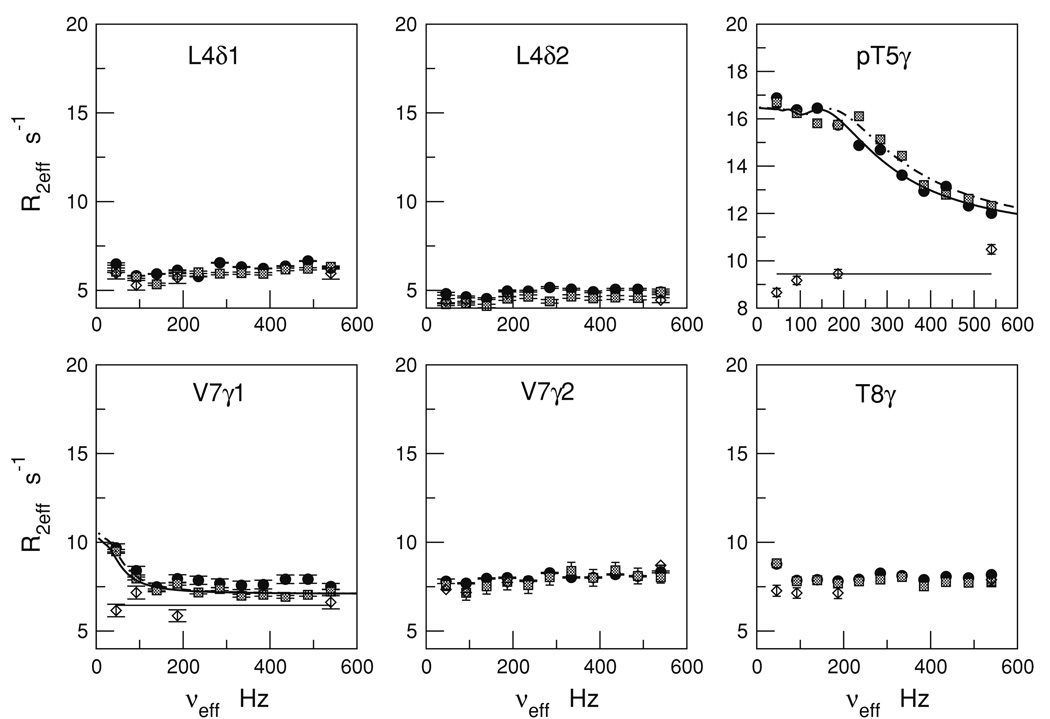
Figure 3 summarizes the R_2eff versus ν_eff profiles for the six well-resolved methyl cross-peaks of the Cdc25 ligand at 278 K. The profiles include dispersion measurements at both 16.4 T (filled circles), and at 18.8 T (hatched squares).

Fig. 3.

¹³CH₃ CPMG relaxation dispersion profiles for the Cdc25 ligand methyls with and without Pin1 at 278 K. The profiles are R_2eff versus ν_eff = 1/2t_cp where, t_cp is the delay between consecutive 180 pulses in the CPMG spin-lock. Ligand R_2eff in the presence of Pin1 are indicated by filled circles (16.4 T) and hatched squares (18.8 T). Free ligand R_2eff (Pin1 absent) at 16.4 T are indicated by the diamonds. The curves are fits to the two-state exchange model using the Carver-Richards expressions (see text). The horizontal lines are the average R_2eff values for the free ligand

The isolated ligand shows no significant dispersion—the R_2,eff versus ν_eff profiles are essentially flat for all methyls. These individual and average values are indicated by the open diamonds and solid horizontal lines, respectively, in Fig. 3. The average and rmsd values of R_2eff at 278 K are as follows: L4-Cδ₁ (5.7 ± 0.2 s⁻¹), L4-Cδ₂ (4.5 ± 0.1 s⁻¹), T5-Cγ (9.4 ± 0.5 ⁻¹), V7-Cγ₁ (6.5 ± 0.4 ⁻¹), V7-Cγ₂ (7.7 ± 0.4 ⁻¹), and T8-Cγ (7.4 ± 0.2 ⁻¹). In the absence of exchange broadening, R_2eff should reflect the ps-ns reorientational dynamics of the methyl ¹³C–¹H bond vectors. Hence, the variations in the free ligand R_2eff most likely reflect the different number of torsion angles separating them from the ligand backbone.

The situation changes in the presence of Pin1. Most methyl carbons remain unaffected. However, pT5-Cγ and V7-Cγ₁ show strong dispersion responses. These dispersion responses occur only upon introduction of Pin1, and are thus a direct consequence of Pin1/Cdc25 ligand interaction. More precisely, interaction with Pin1 at 278 K results in a ligand exchange process that modulates the isotropic ¹³C chemical shifts of both pT5-Cγ and V7-Cγ₁.

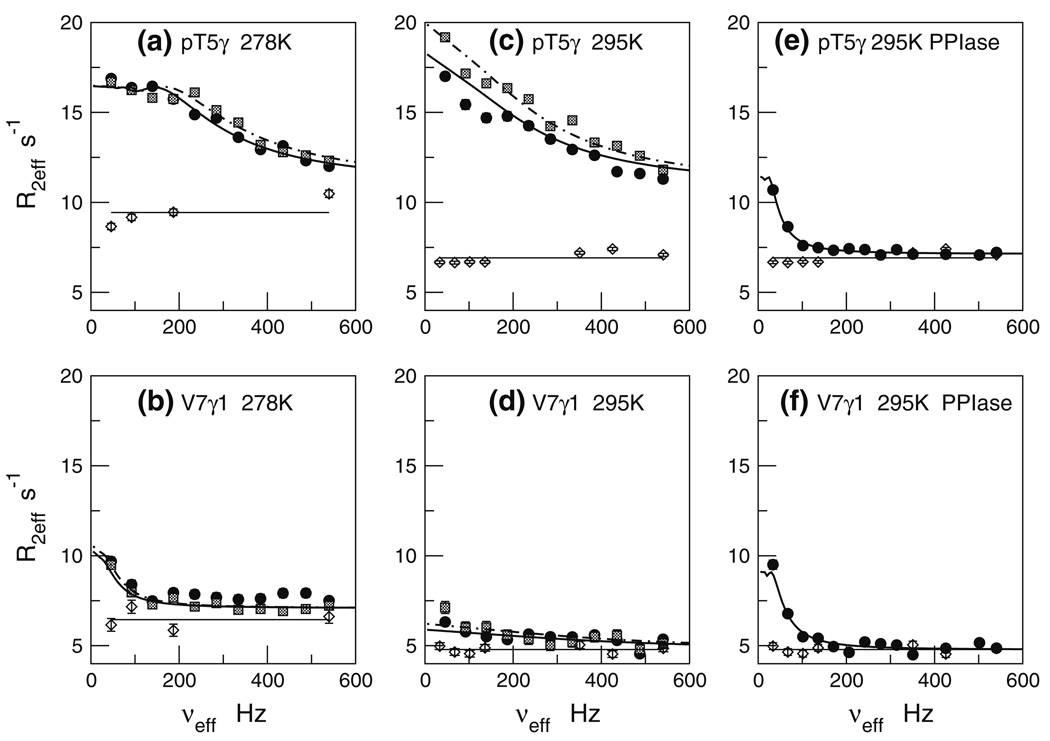
We repeated the methyl dispersion experiments at higher temperature of 295 K. As before, pT5-Cγ and V7-Cγ₁ show clear dispersion profiles, while the other methyls are unresponsive. Figure 4 juxtaposes the R_2eff vs ν_eff profiles at 278 K (panels a, b) versus 295 K (panels c, d), respectively. For pT5-Cγ, we see somewhat larger R_2eff values at 295 K, suggestive of faster chemical exchange at 295 K versus 278 K.

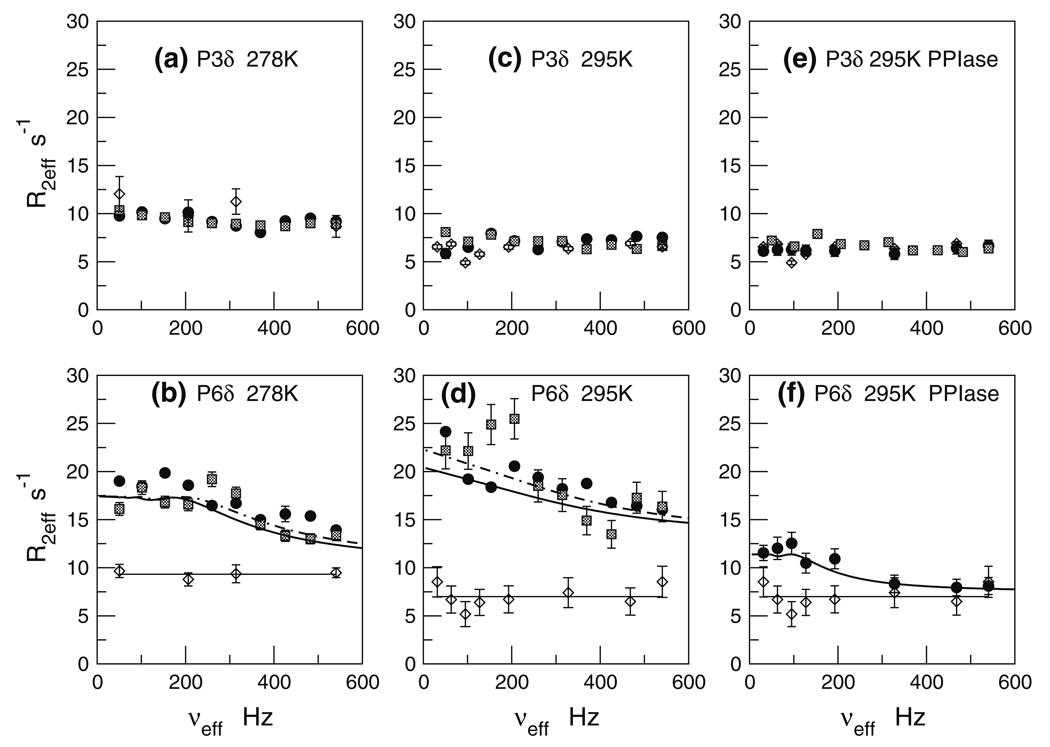
Fig. 4.

¹³CH₃ CPMG relaxation dispersion profiles for pT5-Cγ and V7-Cγ₁ under various conditions. Panels a, b: ligand +/− full-length Pin1 at 278 K; Panels c, d: ligand +/− full-length Pin1 at 295 K; Panels e, f: ligand +/− Pin1-PPIase at 295 K. Symbols, curves, and horizontal lines have the same meaning as in Fig. 3

The selective dispersion pT5-Cγ and V7-Cγ₁ raises the question: what distinguishes these methyls from other ligand methyls in the context of the Pin1/ligand interaction? To address this question, we can turn to the solution structure of the Cdc25 phosphopeptide ligand complexed with the Pin1-WW domain (Wintjens et al. 2001; PDB ID code 1I8G). This structure shows that pT5-Cγ and V7-Cγ₁ are intimately involved in the protein-ligand contact interface, while the other methyl groups are remote. To the extent that these same interactions are preserved when Cdc25 is complexed with the full-length Pin1, this structure provides a basis for understanding the selective dispersion responses of pT5-Cγ and V7-Cγ₁.

Methylene dispersion measurements

For the methylene dispersion measurements, we used the 2-D relaxation dispersion scheme of Mulder et al. which was originally demonstrated on protein ¹⁵NH₂ groups (Mulder et al. 2001b). The ¹³C methylene chemical shifts span a considerable range of ~ 25 ppm. If one is to perform CPMG spin-locking for all methylenes over this range and simultaneously avoid off-resonance artifacts, then the prudent course would be to carry out multiple CPMG dispersion studies with the CPMG spin-lock carrier centered at multiple positions. However, for the Cdc25 ligand, the ¹³C methylene experiments proved considerably less sensitive than the ¹³C methyl experiments. The lower sensitivity limited the time available for multiple CPMG studies. Thus, we focus here only on the proline methylene carbons, P3-Cδ and P6-Cδ, which have nearly the same ¹³C chemical shifts. Notably, P6-Cδ is a priori of interest since it is part of the signature pT-P motif that undergoes Pin1-catalyzed cis-trans isomerization. Figure 5 shows an example spectrum of P3-Cδ and P6-Cδ (in the presence of Pin1), with t_cp set to its longest value of 4.96 ms.

Fig. 5.

Example spectrum from the natural abundance ¹³CH₂ methylene dispersion measurements of the Cdc25 ligand (2 mM), in the presence of 50 µM U-¹⁵N/70%²D Pin1. The spectrum is recorded at 278 K, 16.4 T. The 2-D represents the lowest CPMG frequency ν_eff = 50 Hz. The total CPMG duration was 40 ms. P6-Cδ clearly suffers line-broadening relative to P3-Cδ

We note that the sensitivity of the methylene experiment is further compromised by the fact that the NMR signal from one methylene carbon is divided among two ¹³C–¹H correlations. Thus, as a compensatory measure, we first added the two cross-peak integrals of each methylene prior to extraction of the R_2,eff relaxation rate constants.

Figure 6a and b shows the resulting R_2,eff versus ν_eff profiles at 278 K. The scatter and error bars reflect the lower sensitivity of the methylene experiments, relative to the methyl dispersion. For the isolated ligand, we observe no significant dispersion for either P3-Cδ or P6-Cδ. The R_2,eff versus ν_eff profiles are essentially flat for both methylenes. The average and rmsd values for R_2eff at 278 K are similar for both methylenes: P3-Cδ (10.4 ± 0.9 s⁻¹) and P6-Cδ (9.3 ± 0.3 s⁻¹).

Fig. 6.

¹³CH₂ CPMG relaxation dispersion profiles for P3-Cδ and P6-Cδ under various conditions. Panels a, b: ligand +/− full-length Pin1 at 278 K; Panels c, d: ligand +/− full-length Pin1 at 295 K; Panels e, f: ligand +/− Pin1-PPIase at 295 K. Symbols, curves, and horizontal lines have the same meaning as in Fig. 3. P3-Cδ retains R_2eff values of the free ligand under all conditions

Upon interaction with Pin1, there is a marked change: P6-Cδ shows clear dispersion. By contrast, P3-Cδ remains unaffected. Indeed, this differential behavior is foreshadowed by the differential line-broadening of P6 in Fig. 5.

We repeated the methylene dispersion experiments at the higher temperature of 295 K, and the results are in Fig. 6c and d. The selective dispersion response of P6-Cδ, while noisy, is nevertheless present. The larger scatter and error bars for the 18.8T R_2eff values (hatched squares) are due mainly to poor solvent suppression. We note that the 295 K R_2eff values (Fig. 6c, d) increase from those at 278 K (Fig. 6a, b). This R_2eff increase supports the notion of slow exchange for P6-Cδ at 278 K, nudging towards faster exchange at 295 K. By contrast, the R_2eff of the isolated ligand decreases relative to that at 278 K. Such decreases are of course expected if the free ligand R_2eff lacks contributions from chemical exchange broadening. Then, R_2eff reflects mainly ps-ns motions of the CH bond vector, and so the lower R_2eff likely reflects primarily more rapid tumbling of the ligand at 295 versus 278 K.

The clear dispersion response of P6-Cδ, and the utter lack of response by P3-Cδ is consistent with P6-Cδ being part of the pT-P motif targeted by Pin1. Moreover, the solution structure of the Pin1-WW/Cdc25 ligand complex shows that P6-Cδ forms the central portion of the binding interface, while the P3-Cδ is comparatively remote (Wintjens et al. 2001). Thus, preferential chemical shift modulation of P6-Cδ over P3-Cδ is reasonable.

Extraction of exchange parameters

The above side chain R_2eff vs ν_eff profiles show that the natural abundance ¹³CH₃ and ¹³CH₂ dispersion data are sensitive to the µs-ms dynamics associated with complex formation of a ligand. Specifically, in the presence of Pin1, the methyl carbons of the Cdc25 ligand T5-Cγ and V7-Cγ₁ as well as its methylene carbon P6-Cδ, show temperature-sensitive dispersion profiles. By contrast, the isolated ligand shows no dispersion. Interaction of the Cdc25 ligand with Pin1 selectively modulates the chemical shifts of T5-Cγ, V7-Cγ₁ and P6-Cδ. All of these carbons reside within or flank the pT5-P6 imide linkage, which undergoes Pin1-catalyzed cis-trans isomerization. Additionally, previous structural studies show that these carbons reside within side-chains that make contact with Pin1 (Wintjens et al. 2001). ¹³C chemical shifts are sensitive probes of local structure (torsion angles; Cavalli et al. 2007; Shen et al. 2008; Wishart and Sykes 1994; Xu and Case 2002); hence, the side-chain dispersion profiles reflect, at least in part, ligand conformational reorganization caused by complex formation with Pin1.

To extract quantitative exchange parameters, we fit the R_2eff versus ν_eff dispersion profiles to model functions corresponding to the simplest scenario of two-state exchange. We applied the Carver-Richards model expressions, which contains four adjustable parameters: the net exchange rate constant k_ex, the minor state fractional population p_B, the chemical shift difference between the two states Δ_ppm, and finally the nominal non-exchange relaxation rate R_2,0, which is independent of ν_eff = 1/2t_cp.

For initial guidance, we turned to our recent dispersion measurements of the backbone methine ¹³Cα carbons, for the very same Pin1/Cdc25 interaction (Zintsmaster et al. 2008). In that previous study, Carver-Richards fits of the individual ¹³Cα methines (L4, pT5, P6, and P8) gave very similar exchange parameters. The similarity suggested the appropriateness of a global fit, in which the ¹³Cα nuclei share the same exchange rate constant k_ex and minor species fraction, p_B, but vary site-specifically for the parameters Δ_ppm and R_2,0. Accordingly, after a global fit analysis, we find a global exchange rate constant k_ex = 477 ± 25 s⁻¹ and a minor state fractional population of p_B = 2.4 ± 0.2%. The results are listed in Table 1. Notably, the p_B = 2.4 ± 0.1% coincides with bound ligand fraction, assuming Pin1-saturated conditions. As stated, this assumption is well-founded since our total ligand concentration (2 mM) is much greater than K_D (8 ± 2 µM). It is therefore reasonable to identify the minor state sensed in the backbone dispersion studies as the Pin1-bound ligand. The strong dependence of ¹³Cα shifts on local torsion angles (φ, ψ, χ₁) is well-established (Cornilescu et al. 1999; de Dios et al. 1993; Spera and Bax 1991; Vila and Scheraga 2008; Xu and Case 2002); hence, the methine dispersion likely reflects backbone torsion angle distortions of the ligand upon Pin1 complex formation.

Table 1.

Ligand backbone ¹³Cα global exchange parameters at 278 K

Cα	kex (r/s)	pB	Δppm	R2,0 s−1
L4	477 ± 25	0.024 ± 0.001	1.66 ± 0.04	9.5 ± 0.3
pT5	477 ± 25	0.024 ± 0.001	0.52 ± 0.02	11.7 ± 0.1
P6	477 ± 25	0.024 ± 0.001	0.66 ± 0.02	11.1 ± 0.1
T8	477 ± 25	0.024 ± 0.001	0.67 ± 0.02	8.5 ± 0.1

We then used the backbone-derived k_ex and p_B values as initial values for the side-chain ¹³CH₃ and ¹³CH₂ dispersion data. To our frustration, we found that enforcing one, but not both of these backbone ¹³Cα-derived global values produced satisfactory fits. Nevertheless, we reasoned that it was prudent to identify the minor state as the bound ligand fraction, just as in the backbone studies. Consequently, we set p_B = 2.4% and proceeded with the parameter-fitting. The solid and dashed-dotted curves in Fig. 4 and Fig. 6 shows fits for p_B = 2.4 ± 0.1%; and the results are listed in Table 2. They suggest that at 278 K, T5-Cγ, V7-Cγ1, and P6-Cδ undergo slow exchange on the ¹³C chemical-shift time scale, and transition to fast exchange at 295 K. Specifically, at 278 K, the side chain k_ex rate constants range from 200 to 300 s⁻¹, while at 295 K they range from ~ 1,400 to ~ 2,500 s⁻¹.

Table 2.

Ligand ¹³CH₃ and ¹³CH₂ exchange parameters with full-length Pin1 (Assumes p_B = 0.024 ± 0.001)

Carbon	T (K)	kex (r/s)	Δppm	R2,0 s−1
pT5-Cγ, methyl	278	230 ± 6	1.64 ± 0.30	11.0 ± 0.1
V7-Cγ1, methyl	278	200 ± 7	0.26 ± 0.01	7.1 ± 0.2
P6-Cδ, methylene	278	299 ± 15	1.93 ± 0.08	10.4 ± 0.4
pT5-Cγ, methyl	295	1,360 ± 246	0.67 ± 0.05	10.9 ± 0.5
V7-Cγ1, methyl	295	2,480 ± 570	0.31 ± 0.05	4.8 ± 0.2
P6-Cδ, methylene	295	2,080 ± 233	0.79 ± 0.05	13.1 ± 0.34

What exchange processes underlie the dispersion profiles? At least two processes must be considered: binding to Pin1, and cis-trans isomerization by Pin1. We estimated the cis-trans isomerzation rates from 2-D ¹H–¹H EXSY spectra of Pin1, focusing on the protons directly attached to pT5-Cγ. The EXSY exchange rate constants, k_ex,EXSY, are calculated from exchange cross-peaks that connect major (pT5-Hγ_trans) and minor (pT5-Hγ_cis)) resonances of pT5 (spectra not shown). Hence, k_ex,EXSY is a more exclusive reporter of cis-trans isomerization. We found k_ex,EXSY = 5.5 ± 0.3 s⁻¹ (278 K) to k_ex,EXSY = 8.8 ± 0.4 s⁻¹ (295 K). These values are quite low compared to the ¹³C side-chain dispersion derived k_ex values in Table 2. Thus, the k_ex values from the side-chain ¹³CH₃ and ¹³CH₂ dispersion profiles, as well as the backbone, most likely reflect binding rather than cis-trans isomerization. This is reasonable, given that exchange rate constant for ligand binding, under protein saturated conditions, is k_ex,binding = k_onK_D. Assuming the on-rate k_on is diffusion-limited, then k_on ≤ 1 × 10⁸ M⁻¹ s⁻¹ (Davis et al. 1994). As stated, the Cdc25 ligand K_D = 8 ± 2 µM, and so we would expect k_ex,binding to be ≤800 s⁻¹. This estimate is in far better agreement with the side chain ¹³C dispersion derived k_ex values of 200–300 s⁻¹ and the backbone k^ex values of 477 ± 25 s⁻¹. At the same time we acknowledge the mismatch between these side chain and backbone k_ex values. The mismatch suggests that side chain and backbone experience different exchange processes.

Further interpretation of these results demands caution. As stated, Pin1 consists of two domains: a catalytic PPIase domain, and the smaller WW domain. Both domains can bind the pT-P motif. The distinction is that the PPIase domain is solely responsible for cis-trans isomerization. Thus, the ¹³C dispersion data could reflect interaction with either the PPIase or WW domain active sites. Moreover, the complex formation with the PPIase domain could involve conformational adjustments pertinent to both binding and cis-trans isomerization. These issues raise the possibility that the dispersion profiles in Fig. 4a–d and in Fig. 6a–d reflect more than one exchange process—that is, the exchange scheme may involve more than two chemical states.

Comparison with truncated Pin1 construct indicates multiple exchange processes

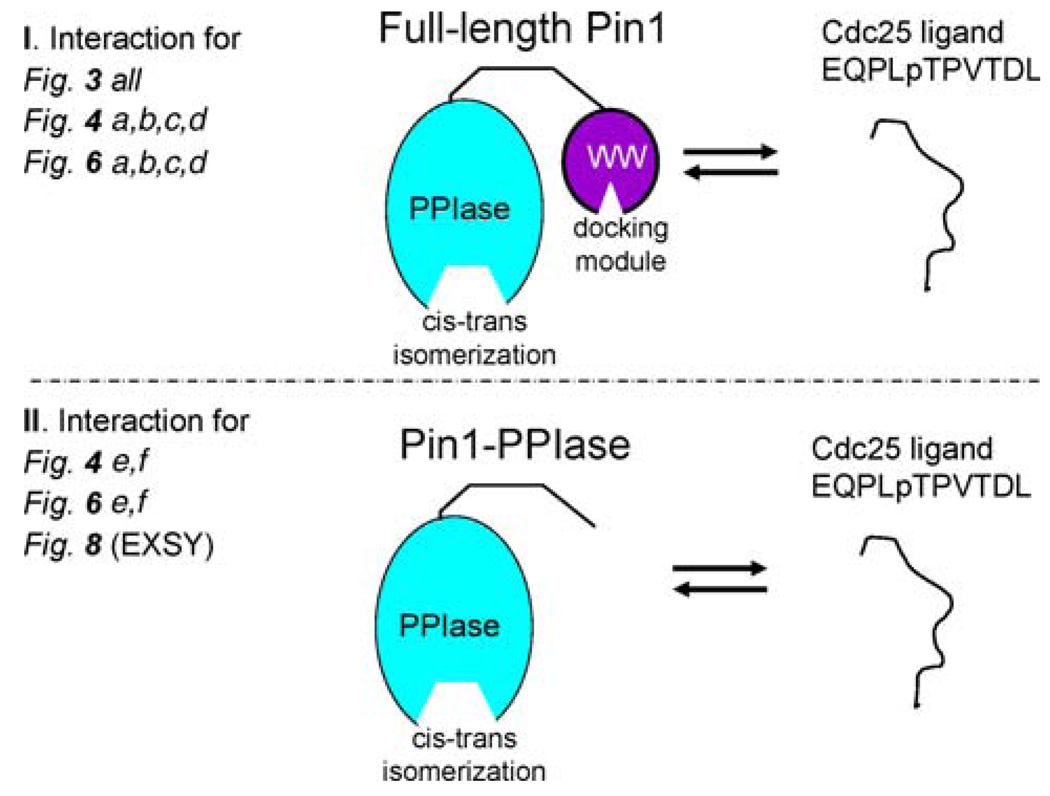
To shed light on the above possibility, we generated a truncated Pin1 construct that omits the Pin1-WW domain. We refer to this shortened construct as Pin1-PPIase. Pin1-PPIase is necessary and sufficient for in vitro isomerase activity (Labeikovsky et al. 2007; Verdecia et al. 2000). This construct removes the effects of WW domain binding; hence, the ¹³C dispersion profiles solely reflect interaction with the PPIase active site. Figure 7 schematizes this shorter construct, and contrasts it with the full-length situation above. Henceforth, Pin1-PPIase refers to the bottom panel of Fig. 7, while Pin1 (i.e., the full-length protein that has been discussed in the preceding sections above) refers to the top panel of Fig. 7.

Fig. 7.

Schematic of interactions described in this study. The top interaction (I): ligand +/− full-length Pin1. Full-length Pin1 has two domains, both of which can individually bind the ligand; the smaller WW domain (purple), which serves as a pure docking module, and the larger PPIase domain (aqua), which is solely responsible for cis-trans isomerization. The full-length Pin1 interaction is pertinent to the ¹³C dispersion studies in all of Fig. 3, Fig. 4a–d, and Fig. 6a–d. The bottom interaction (II): ligand +/− Pin1-PPIase. The shorter Pin1-PPIase construct omits the WW domain, thus simplifying the system to just the active site of the PPIase domain. The Pin1-PPIase interaction is pertinent to the ¹³C dispersion studies profiled in Fig. 4e and f and 6e, f, as well as the 2-D ¹H–¹H EXSY study of Fig. 8

We repeated the ¹³C methyl and methylene dispersion experiments for the Cdc25 ligand at 295 K, 16.4 T (700 MHz) in the presence of Pin1-PPIase. The resulting R_2eff versus ν_eff dispersion are in Fig. 4e and f and Fig. 6f. Comparisons with Fig. 4c, d for the methyls, and Fig. 6d for the methylenes, show that the Pin1-PPIase profiles are markedly different from that seen with full-length Pin1. These differences are particularly evident for the methyls. First, the maximum R_2eff value for pT5-Cγ in Pin1-PPIase (panel e) is much lower than that previously seen for full-length Pin1 (panel c). Second, the dispersion curve descends to its plateau at much lower frequency (ν_eff < 100 Hz) than in full-length Pin1, suggesting a significantly slower k_ex value. Third, the R_2eff values at higher ν_eff (shorter t_cp) are now same as that of the isolated (free) Cdc25 ligand. This last point is critical: recall the free ligand shows no significant dispersion. Hence, we are assured that the plateau R_2eff values for pT5-Cγ and V7-Cγ₁ in Fig. 4e and f are “exchange-free”. In the case of interactions with full-length Pin1, only V7-C γ1 at 295 K came close to such behavior.

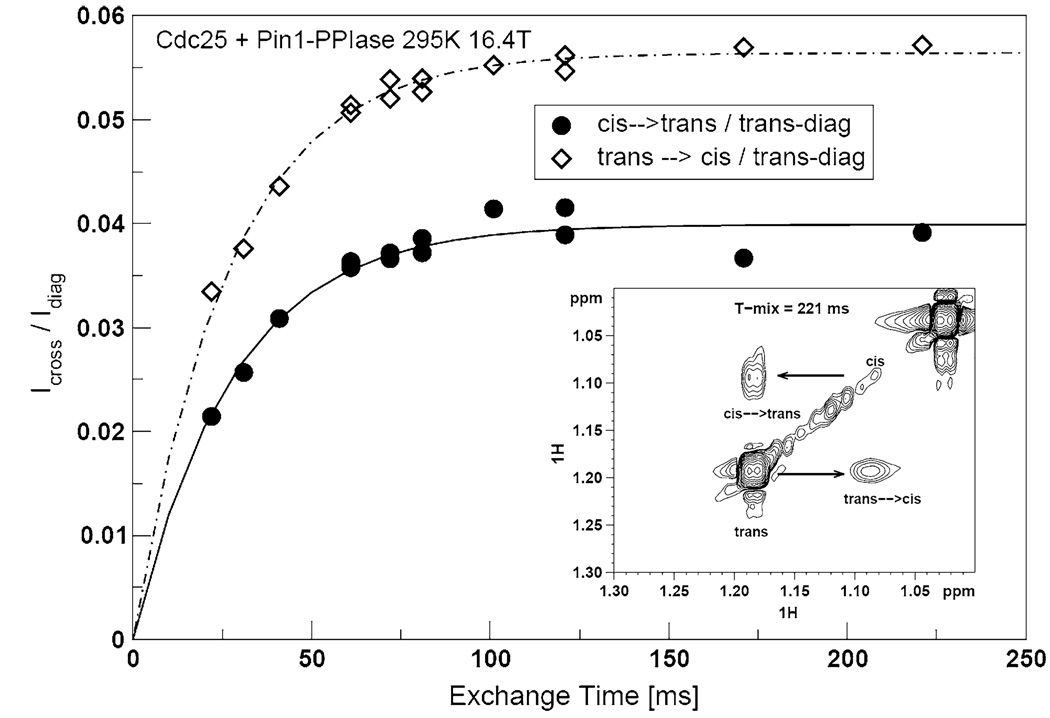
We then tried to fit the pT5-¹³Cγ and V7-¹³Cγ1 methyl dispersion profiles to the Carver-Richards two-state exchange model. The k_ex values, previously obtained from the studies with full-length Pin1 (Fig. 4c, d), were far too large to produce satisfactory fits. Consequently, we tried the cis-trans isomerization rate constant, k_ex,EXSY = 37 ± 1.1 s⁻¹, obtained from the 2-D ¹H–¹H EXSY spectra of pT5-¹Hγ, in the presence of the shorter Pin1-PPIase construct at 295 K. (Note that this EXSY experiment, performed on the truncated Pin1-PPIase construct, is distinct from that already described for full-length Pin1). Figure 8 shows an example of the EXSY spectra and corresponding build-up curves. We also used the free ligand average R_2eff for the initial value of R_2,0. The results of the parameter search are the curves in Fig. 4e and f and Fig. 6f. The numerical values are listed in Table 3. The cis-trans isomerization exchange rate fits the methyl T5-Cγ, V7-Cγ₁ profiles and P6-Cδ methylene profile remarkably well. Moreover, we find that the minor state fractional population p_B is ~ 11 ± 2%. This percentage is in excellent agreement with the minor cis populations of the Cdc25 ligand estimated from integrations of the 1-D 1H spectrum. Hence, in the simplified system consisting of the truncated Pin1-PPiase construct, the ¹H–¹H EXSY and side chain ¹³CH₃ and ¹³CH₂ dispersion data report on the same exchange process: cis-trans isomerization of the pT-P motif in Cdc25 by Pin1-PPIase.

Fig. 8.

Example of ¹H–¹H EXSY of 2 mM Cdc25 in the presence of 50µM Pin1-PPIase at 295 K, 16.4 T. The build-up curves and spectra for methyl protons of pT5

Table 3.

Ligand ¹³CH₃ and ¹³CH₂ exchange parameters with Pin1-PPIase at 295 K and 16.4 T

Carbon	kex (r/s)	pB	Δppm	R2,0 s−1
pT5-Cγ, methyl	40 ± 2	0.11 ± 0.002	0.26 ± 0.02	7.1 ± 0.1
V7-Cγ1, methyl	40 ± 2	0.11 ± 0.002	0.33 ± 0.03	4.8 ± 0.1
P6-Cδ, methylene	39 ± 2	0.10 ± 0.002	1.05 ± 0.42	7.5 ± 0.8

The new information provided by the ¹³C side-chain dispersion that is not available from the ¹H–¹H EXSY data are the ¹³C chemical shift differences between the cis and trans conformers. The ¹³C chemical shifts are sensitive to local structure; hence, the dispersion data provides potential insight into the side-chain conformational transitions needed for cis-trans isomerization.

Note that we do not directly observe minor cis ¹³C methyl cross-peaks in the 2-D ¹³C–¹H dispersion spectra—they are “invisible” (Mulder et al. 2001a). This is likely due to the sensitivity associated with natural abundance ¹³C, and the expected greater broadening of the minor species in a two-state exchange scenario that is slow on the chemical shift time scale (Ishima and Torchia 1999; Millet et al. 2000). The ability of these dispersion measurements to provide information concerning the side-chain ¹³C chemical shifts—site specific conformational parameters—sheds new light on the exchange process.

In summary, the results from the truncated Pin1-PPIase construct (Fig. 4e, f, and Fig. 6f) strongly suggest that the dispersion profiles for Cdc25 in the presence of full-length Pin1 (Fig. 4a–d, Fig. 6a–d.) reflect more than one exchange process. In essence, the dispersion data from the truncated Pin1-PPIase construct exposes an otherwise “invisible” exchange process masked within the dispersion profiles obtained from full-length Pin1. Thus, the exchange parameters obtained for these profiles are meaningful if the exchange behavior is that of a quasi-two-state process; such a scenario is conceivable if the constituent exchange processes have very different k_ex values (Grey et al. 2003). This is likely the case here since cis-trans isomerization and binding rates differ by at least an order of magnitude.

Concluding remarks

The results of this work show that ¹³CH₃ and ¹³CH₂ relaxation dispersion studies can give insights into the µs-ms conformational transitions (reorganization) required of a ligand for biological activity. In particular, via studies of the interaction between Pin1 and its Cdc25 ligand, we have shown that the dispersion studies can give insight into the ligand motions necessary for protein complex formation and catalysis The resulting dispersion data yields site-specific exchange rate constants, populations, and critically, ¹³C chemical shift differences, which are in principle sensitive to changes in the ligand conformational ensemble.

A caveat should be noted: while side-chain ¹³C chemical shifts are sensitive to local conformation (e.g., side-chain torsion angles), environmental factors (e.g., electric fields, ring current shifts, and changes in solvent exposure) can also play a role. From the dispersion data alone, it is not obvious whether conformational or environmental influences dominate. Recent computational and solid-state NMR studies lend support for the conformational dependence for methyl ¹³C shift changes (Hong et al. 2009; London et al. 2008). Nevertheless, a conformational interpretation of our side chain ¹³C relaxation dispersion requires caution. Complementary dispersion experiments of the Pin1 catalytic site, as well as ligand NOESY experiments should help shed light on the dominant chemical shift effects.

From the narrower perspective of understanding the Pin1/Cdc25 ligand interaction, clearly more work remains to be done. For example, we must further measure Cdc25 ligand dispersion in the presence of Pin1-WW domain. Combining such studies with those of the isolated Pin1-PPIase domain above should help enable a more quantitative deconvolution of the dispersion data seen in the presence of full-length Pin1, and help rationalize the apparent differences between backbone and side chain exchange parameters. Such work is in progress. Nevertheless, to the extent that the chemical shifts are dominated by conformational effects, the data presented thus far clearly shows that functionally relevant conformational transitions of the ligand can be described by side-chain relaxation dispersion.

In our study, we have focused on a flexible, peptidic ligand with modest (µM) binding affinity. Such ligands are common in the early stages of drug discovery. What about tight binding (e.g., nano-molar) ligands? In this case, the concentration of the ligand is that of the target protein. Hence, the above dispersion experiments would require either higher protein concentrations ( ~ 500 µM), or isotope-labeled ligands. While we pointed above to the typical paucity of labeled ligands in pharmaceutical research settings, it is also true that if the ligand actually is a tighter binder, then there is likely to be greater interest in taking extra measures to synthesize labeled ligands.

Flexible drug-like molecules typically adopt bound conformations that do not correspond to the conformational energy minima of the free state (Perola and Charifson 2004). This means complex formation introduces new intermolecular interactions that distort conformational energy landscape of the ligand. In turn, this distortion drives conformational reorganization of the ligand upon complex formation. Such re-organization can be thought of as “induced fit” if the free ligand conformational ensemble lacks the bound conformer(s), or “conformational selection” if the free ligand ensemble already fleetingly samples its bound conformer(s). In either scenario, the ¹³CH₃ and ¹³CH₂ relaxation dispersion studies can serve as tools to describe the underlying conformational transitions associated with this re-organization.

We are particularly encouraged by the effectiveness of the ¹³CH₃ dispersion measurements. In typical pharmaceutical research settings, isotope-enriched ligands are a rarity due to cost and syntheses considerations, and this elevates the necessity for ¹³C experiments to be performed at natural abundance. The high sensitivity afforded by the methyl moiety is well-suited to such natural abundance ¹³C work. Moreover, methyls are among the most prevalent side chains in drug-like molecules (Bemis and Murcko 1999). Hence, the methyl dispersion experiments should find applicability to a broad range of ligand classes relevant for drug research.

Finally, while our illustration has focused on the Pin1/Cdc25 system,we stress that this strategy is relevant for ligand re-organization problems, in general. In fact, by combining these side-chain ¹³C dispersion parameters with those of the backbone (Zintsmaster et al. 2008), it should be possible to get a more detailed picture of the conformational distortions the ligand undergoes upon formation of the protein-ligand complex. This may be particularly useful when the three-dimensional structure of the drug-target is unavailable, and therefore, ligand-based approaches focused on pharmacophore development must be adopted (see e.g., van Drie 2003). Integral membrane proteins, such as GPCRs are a well-known example. Alternatively, ligand re-organization may also be important for membrane binding or membrane permeability. Knowing where and how a flexible ligand undergoes conformational changes as a consequence of crossing biological barriers may suggest design strategies for improving ADME properties and oral bioavailability (Navia and Chaturvedi 1996; Veber et al. 2002). In this context, the ¹³C dispersion experiments described above can shed light on the site-specific conformational changes required for complex formation and drug delivery and thus, help guide strategies of ligand modification aimed at improving activity.