Force Generation in Lamellipodia Is a Probabilistic Process with Fast Growth and Retraction Events

Abstract

Polymerization of actin filaments is the primary source of motility in lamellipodia and it is controlled by a variety of regulatory proteins. The underlying molecular mechanisms are only partially understood and a precise determination of dynamical properties of force generation is necessary. Using optical tweezers, we have measured with millisecond (ms) temporal resolution and picoNewton (pN) sensitivity the force-velocity (Fv) relationship and the power dissipated by lamellipodia of dorsal root ganglia neurons. When force and velocity are averaged over 3–5 s, the Fv relationships can be flat. On a finer timescale, random occurrence of fast growth and subsecond retractions become predominant. The maximal power dissipated by lamellipodia over a silica bead with a diameter of 1 μm is 10⁻¹⁶ W. Our results clarify the dynamical properties of force generation: i), force generation is a probabilistic process; ii), underlying biological events have a bandwidth up to at least 10 Hz; and iii), fast growth of lamellipodia leading edge alternates with local retractions.

Introduction

Neurons are among the most specialized cells in living organisms and are capable of self-organization in complex networks. To self-organize, neurons protrude neurites, highly motile structures that explore the environment in search of appropriate chemical cues necessary for the formation of correct synaptic connections (1,2). Neurite exploration is guided by the growth cone located at the neurite tip (3–5) that is formed by an extended lamellipodium from which thin filopodia emerge (6). Filopodia tips can move at a velocity that can reach 0.8–1 μm/s and their motility is at the basis of the efficient formation of neural networks. The primary source of motility in growth cones is the polymerization of actin filaments (7–9), a process controlled by a variety of regulatory proteins (10). The addition of actin polymers to actin filaments in close contact with the membrane pushes the cellular membrane forward exerting a protrusive force (11,12).

The overall dynamics regulating this process is not yet clear, and mathematical modeling provides a way to link known molecular events to force generation (13). A key outcome of these models is represented by the Fv relationships, describing how the force (F) exerted by the actin filament network is related to the velocity (v) of their growing ends (7,14–19). Fluctuations of contact between the tips of actin filaments and the surrounding membrane is an essential feature of Brownian ratchet models (7,15,16) leading to Fv relationships in which v decreases exponentially with increasing values of F. In autocatalytic models (14,16,17), when an obstacle is encountered, the actin network—due to the activity of controlling proteins—originates new branches, so that the velocity v remains constant for increasing values of F.

Previous determinations of the Fv relationships (20) with an atomic force microscope (AFM) cantilever (21,22) had a limited time resolution and were obtained either in vitro or in migrating keratocytes exerting forces in the nanoNewton range. In this work, using optical tweezers (23–25), we provide an experimental characterization of Fv relationships in neuronal growth cones with millisecond resolution and picoNewton sensitivity. Bold notations x, v, and F indicate vectorial quantities, and x, v, and F indicate either the modulus or a component of these vectors. This experimental technique enabled us to determine the three components of the force exerted by a lamellipodium, F = (F_x, F_y, F_z), from rat dorsal root ganglia (DRG) and of the velocity of its leading edge, v = (v_x, v_y, v_z). From these vectorial quantities, we have derived properties of force generation in lamellipodia, with important biological consequences. We found that force generation in lamellipodia is an intrinsically multiscale process. At a temporal resolution of 3–5 s, the exerted force can increase, maintaining a constant velocity. At a millisecond resolution, a much more complex behavior is observed, with random occurrence of fast growths and subsecond retractions. Our results show that autocatalytic models (14,16,17) of force generation are correct in a mean or average approximation. At a higher temporal resolution, the network of actin filaments evolves in a much more complex manner that can be characterized only probabilistically.

Materials and Methods

Neuron preparation

Wistar rats at postnatal days 10–12 (P10–P12) were sacrificed by decapitation after anesthesia with CO₂ in accordance with the Italian Animal Welfare Act. After dissection, DRGs were incubated with trypsin (0.5 mg/ml; Sigma Aldrich, Milan, Italy), collagenase (1 mg/ml; Sigma Aldrich), and DNase (0.1 mg/ml; Sigma Aldrich) in 5 ml Neurobasal medium (Gibco, Invitrogen, Milan, Italy) in a shaking bath (37°C for 35–40 min). After mechanical dissociation, they were centrifuged at 300 rpm, resuspended in culture medium, and plated on poly-L-lysine-coated (0.5 μg/ml; Sigma Aldrich) coverslips. Neurons were incubated for 24–48 h and nerve growth factor (50 ng/ml; Alomone Labs, Jerusalem, Israel) was added before performing the measurements.

Optical tweezers setup

The optical tweezers set-up was built as described by Cojoc et al. (25). Briefly, the trapping source was an ytterbium fiber laser operating at 1064 nm (IPG Laser GmbH, Burbach, Germany), which was sent onto an inverted microscope (IX81, Olympus, Milan, Italy) to the focusing objective (Olympus 100× oil, NA 1.4), as shown in the schematic diagram of Fig. S1 in the Supporting Material. The dish containing the differentiating neurons and the beads (PSI-1.0NH2, G. Kisker GbR, Steinfurt, Germany) was placed on the microscope stage, which could be moved by a three-axis piezoelectric nanocube (17 MAX 301, Melles Griot, Albuquerque, NM). The temperature of the dish was kept at 37°C by a Peltier device. The dish was maintained in an environment with a controlled level of CO₂ (5%) and moisture (95%). The bead position x = (x, y, z) was determined along all the axes with an accuracy of 2 nm using back focal plane detection, which relies on the interference between forward scattered light from the bead and unscattered light (24,26,27). The back focal plane of the condenser was imaged onto a quadrant photodiode (QPD) (C5460SPL 6041, Hamamatsu, Milan, Italy), and the light intensity was converted to differential outputs digitized at 20 kHz and low-pass filtered at 5 kHz. The z position of the bead was determined using the Gouy phase-shift effect (24). The trap stiffness, K_x,y,z = (k_x, k_y, k_z), and the detector sensitivity were calibrated using the power spectrum method (24). Detector sensitivity was also checked by measuring voltage signals originating from displacements of a bead stuck to the coverslip obtained with the three-axis piezoelectric nanocube. The force exerted by the lamellipodium, F, was taken as equal to −F_trap. When the displacement of the bead from its equilibrium position inside the trap, d = (d_x, d_y, d_z), was <400 nm, F_trap = (F_x, F_y, F_z) was calculated as F_x = d_xk_x, F_y= d_yk_y, and F_z = d_zk_z (24). All experiments of force recordings were monitored by video imaging with a charge-coupled device (CCD) camera at a frame rate of 5 Hz. Visual inspection of recorded images made it possible to discard from the analysis all force recordings during which visible debris interfered with the optical determination of bead position x.

Bandwidth of biological events underlying force generation

A reliable and accurate computation of Fv relationships from the bead displacement x and force F requires a careful analysis of time series obtained from digitization of the three components of x. When the velocity, v = (v_x, v_y, v_z), is derived from the bead displacement x by numerical differentiation, it is necessary to low-pass filter the original data, as spurious high frequencies amplify noise (28). To find the appropriate cut-off frequency, we investigated the bandwidth of biological events underlying force generation. We computed and compared the power spectrum density of forces measured far from any neuron (PSD_noise(f); Fig. 1 a, red traces)—originating from Brownian fluctuations and instrumental noise—and the PSD_push(f) of forces measured when the leading edge of the lamellipodium pushed the bead (Fig. 1 a, blue traces). PSD_noise(f) and PSD_push(f) are very similar, and almost indistinguishable for f > 30 Hz, but at frequencies below 1 Hz the energy of PSD_push(f) is at least 30 times larger than that caused by Brownian collisions. The analysis of PSD_noise(f) and PSD_push(f) in 14 experiments indicates that the bandwidth of biological events underlying force generation in DRG lamellipodia extends up to 10 Hz. Therefore, events occurring on a timescale of 100 ms cannot be neglected, and force generation needs to be analyzed at a higher temporal resolution than in previous investigations.

Figure 1.

Computation of Fv relationships. (a) Power spectrum density of forces measured far from the lamellipodium (red trace) and when the lamellipodium pushed the bead (blue trace), computed from the red and blue traces, respectively, shown in the inset. Green, pink, and black arrows indicate 0.2, 1, and 10 Hz, respectively. (b) Fv relationships computed with Gaussian filtering at 0.2 Hz (green) and linear regression with W = 10,000 (gray), as described in Materials and Methods. The green dotted line represents −3σ_v at the 0.2-Hz bandwidth (where σ_v was calculated from bead fluctuations measured away from the lamellipodia). (c) Relationship between the standard deviations of velocity distribution as a function of smoothing for two values of the trap stiffness, 0.005 pN/nm (squares) and 0.045 pN/nm (circles).

Computation of Fv relationships

The velocity, v = (v_x, v_y, v_z), of the bead was obtained by numerical differentiation of its sampled position x = (x(n), y(n), z(n)) n = 1,…N. Numerical differentiation was computed either by convolution of position components x(n), y(n), and z(n) with the derivative of a Gaussian filter 1/[σ(2π)^1/2] exp(−t²/σ²) (Gaussian filtering) or by linear regression. Gaussian filters corresponding to cut-off frequencies of 0.2, 1, and 10 Hz were used (see Figs. 4–6). In the linear regression method, the components v_x(n), v_y(n), and v_z(n) of velocity v were calculated by a linear least-square fit of the equations x(n) = a_x + v_x(n) (i − n)Δt, y(n) = a_y + v_y(n) (i − n)Δt, and z(n) = a_z + v_z(n) (i − n)Δt with i = −W,…,W, where Δt was the sampling interval. The two parameters a_x and v_x(n) were determined by minimizing the cost function

$$\left[v_x,a_x\right]=\underset{[v,a_x]}{\mathrm{arg\; min}}\left[\sum _{i=n-W}^{n+W}{\left(a_x+v_x(i-n)\Delta t-y\left(i\right)\right)}^2\right]\text{.}$$

a_y and v_y(n), and a_z and v_z(n), were determined in a similar way. Computation of derivatives with the linear regression method depended on the number of samples, W.

Figure 4.

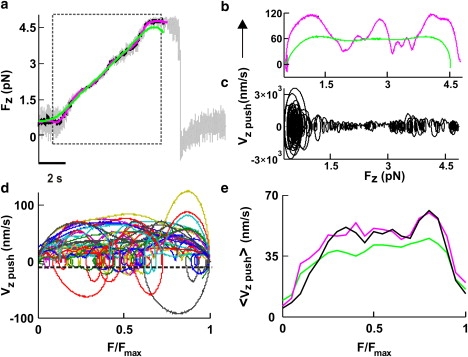
Fv relationships when lamellipodia lifted up the bead along the z direction. (a) The F_z component of the force when the lamellipodium of Fig. 2 pushed the bead vertically. The dotted box indicates the section of force measurement used to compute the Fv relationship after Gaussian filtering at 0.2 (green), 1 (pink), and 10 Hz (black). (b and c) Fv relationships obtained after smoothing at 0.2 Hz (b, green trace) and 1 Hz (b, pink trace) and at 10 Hz (c). (d) Superimposed Fv relationships from 29 experiments normalized to F_max from data filtered at 0.2 Hz. The black line represents −3σ_v at the 0.2-Hz bandwidth (where σ_v was calculated from bead fluctuations measured away from the lamellipodia). (e) <Fv>_x relationships normalized to F_max. Data were filtered up to a bandwidth of X Hz. <Fv>_0.2 (green), <Fv>₁ (pink), and <Fv>₁₀ (black).

Figure 5.

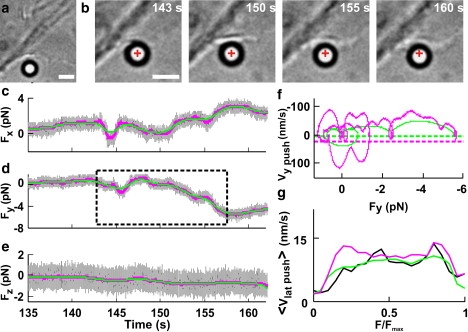
Fv relationships when a lamellipodium pushed the bead laterally along the xy direction. (a) Low-resolution image of a lamellipodium near the trapped bead. Scale bar, 2 μm. (b) Micrographs of the lamellipodium pushing the bead laterally during its protrusion. Images were taken at different times during force generation (see c–e). The cross indicates the center of the optical trap. Scale bar, 2 μm. (c–e) The three force components, F_x, F_y, and F_z (gray traces), without filtering and after Gaussian filtering at 0.2 and 1 Hz (green and pink traces, respectively). The dotted box in d indicates the section of the recording used to compute the Fv relationships in f. (f) Fv relationships computed with Gaussian filtering at 0.2 and 1 Hz (green and pink traces, respectively) from a lateral component of the force F_y. Dotted green and pink lines represent −3σ_v at the 0.2- and 1-Hz bandwidths, respectively (where σ_v was calculated from bead fluctuations measured away from the lamellipodia). During the push, F_y becomes negative, and transient retractions are therefore associated with positive velocities. (g) <Fv>_x relationships normalized to F_max from 22 experiments. Data were filtered up to a bandwidth of X Hz. <Fv>_0.2 (green), <Fv>₁ (pink), and <Fv>₁₀ (black).

Figure 6.

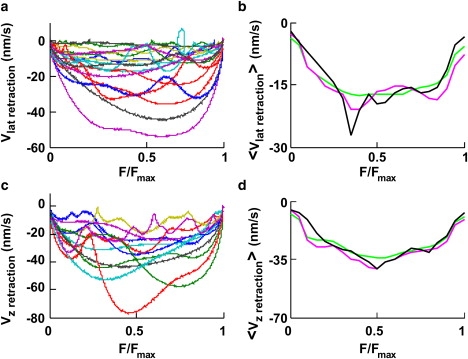
Fv relationships during retractions. (a and c) Superimposed Fv relationships from 18 lateral and 12 vertical retractions, respectively, from data filtered at 0.2 Hz. F is normalized to F_max. (b and d) <Fv>_x relationships for lateral (21 experiments) and vertical (22 experiments) retractions, respectively. Data were filtered up to a bandwidth of X Hz. <Fv>_0.2 (green trace), <Fv>₁ (pink trace), and <Fv>₁₀ (black trace).

Fv relationships computed from vertical and lateral pushes had periods of negative velocity (see Figs. 4 c and 5 f), corresponding to transient retractions of the lamellipodium leading edge. When the velocity reverses its direction, becoming negative, the same force can be exerted for two different values of the velocity, leading to the appearance of loops in Fv relationships (see Fig. 4 c), typical of systems exhibiting hysteresis (21). Because of the limited spatial and temporal resolution of the CCD camera used in this study, these transient retractions could not be confirmed by video imaging. Therefore, we asked whether these loops could originate from numerical artifacts and noise fluctuations. Indeed, the numerical computation of derivatives from noisy data is ill-conditioned (28), and negative velocities could be produced by the specific method used to compute the velocity from the displacement. For this reason, we compared two different methods to obtain the velocity, v, from the displacement: Gaussian filtering and linear regression. In these two methods, the timescale is given by the cut-off frequency of the Gaussian function and by the number of points in the window (W), respectively. Fv relationships obtained from the same force measurement sampled at 10 kHz with the linear regression method with W = 10,000 (Fig. 1 b, gray trace) and obtained by using a Gaussian filter with a cut-off frequency of 0.2 Hz (Fig. 1 b, green trace) had the same shape and number of loops.

As numerical differentiation is very sensitive to noise and amplifies its high-frequency components, we investigated to what extent loops could be caused by Brownian fluctuations. We computed Fv relationships from force measurements obtained far from lamellipodia. The obtained velocity was Gaussian-distributed around 0, with a standard deviation of σ_v increasing with the bandwidth of Gaussian filtering, depending also on the trap stiffness (Fig. 1 c). Periods with a negative velocity observed during vertical and lateral pushes, during which v was <−3σ_v, could not be ascribed to Brownian fluctuations, and all negative velocities exceeding −3σ_v lines (Fig. 1 b, horizontal lines; and see Figs. 4 d and 5 f,) were caused by transient retractions of the lamellipodium.

AFM imaging

The three-dimensional (3D) structure of DRG lamellipodia (Fig. 2 a) was determined by using AFM, as shown in. Before imaging with AFM, DRG neurons were fixed with glutaraldehyde (Sigma Aldrich). DRG growth cones were imaged using a commercial AFM (Nanowizard II, JPK, Berlin, Germany) combined with an inverted optical microscope (Axiovert 200, Zeiss, Milan, Italy). Soft tips with low force constant (OBL, 0.03N/m; Veeco, Santa Barbara, CA) were utilized, and forces were kept between 100 pN and 1 nN during scanning.

Figure 2.

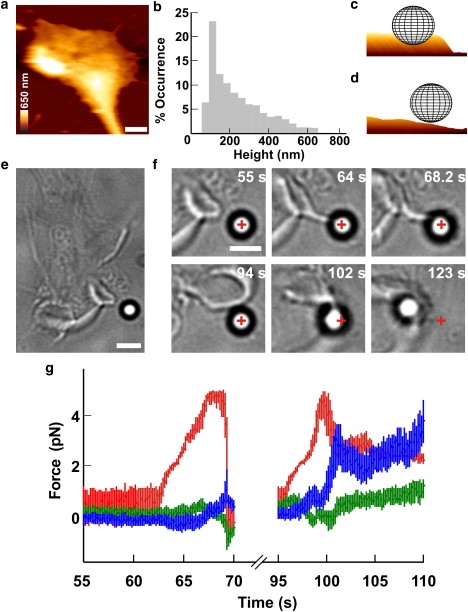
Push and retraction by a lamellipodium. (a) AFM image of a lamellipodium. The height is coded as in the colored scale bar and horizontal white scale bar, 2 μm. (b) Occurrence histogram of measured height of lamellipodium leading edges from seven growth cones. (c and d) Three-dimensional representations of a 1-μm bead in front of a thick (c) and a thin (d) lamellipodium. (e) Low-resolution image of a lamellipodium in front of a bead trapped with an infrared laser. Scale bar, 2 μm. (f) Successive frames showing the lamellipodium (55 s) growing toward the bead (64 s) and lifting it up (68.2 s). Subsequently, the lamellipodium retracted (94 s) and grew under the bead pulling it out of the trap during retraction (102–123 s). The cross indicates the center of the optical trap. Scale bar, 2 μm. (g) The three components F_x (blue), F_y (green), and F_z (red) of the force when the lamellipodium pushed the bead vertically (55–70 s) and when the lamellipodium lifted up and retracted (95–110 s).

Results

DRG neurons isolated from P10–P12 rats were plated on poly-L-lysine-coated glass coverslips positioned on the stage of an inverted microscope used for imaging and measuring forces (see Materials and Methods). After 1 or 2 days of incubation, neurites emerged from the DRG soma and their motion was analyzed. Filopodia and lamellipodia moved rapidly, exploring the 3D space in all directions. DRG lamellipodia were imaged with AFM (Fig. 2 a) and the height of their leading edges varied from 45 to 660 nm (Fig. 2 b). Silica beads of 1-μm diameter were trapped with a 1064 nm infrared (IR) laser tweezers and positioned in front of the leading edge of a lamellipodium (Fig. 2 e). When the center of the bead is located at ∼800 nm above the coverslip, a thick lamellipodium can push the bead (Fig. 2 c). Visual inspection of lamellipodia indicates the existence of several stereotyped behaviors (29): the lamellipodium grows underneath the bead without displacing it (Fig. 2 d and Fig. S2); the bead adheres to the cell membrane, and when the lamellipodium retracts, the bead is removed from the trap (Fig. 2 f, 102 s); the lamellipodium grows underneath the bead, displacing it upward (Fig. 2 f, 68.2 s) (30); or the lamellipodium pushes the bead forward exerting a force in the direction of its growth (see Fig. 3, a and b). Often, two or more of these stereotyped behaviors were observed in the same experiment. In the example of Fig. 2 f, the lamellipodium initially pushed the bead upward (Fig. 2 g, 64–68.2 s) and, after the lamellipodium retracted the bead, returned inside the trap (94 s). After a few seconds, the lamellipodium lifted up the bead again, and, because of the presence of adhesion forces, the bead remained attached to the lamellipodium membrane. Finally, the lamellipodium retracted, pulling the bead away from its trap (Fig. 2 g, 95–110 s). Adhesion of the bead to the lamellipodium was often irreversible and could not be detached from the lamellipodium by increasing the power of the laser beam, but in other experiments, adhesion was reversible and the bead detached spontaneously. In all experiments, the growth cone behavior was followed with video imaging and the displacement of the bead, x = (x, y, z), was measured with a high temporal resolution using a QPD. The z axis is perpendicular to the coverslip and parallel to the IR laser beam used for trapping. By determining the trap stiffness, k = (k_x, k_y, k_z), F was obtained as (−xk_x, −yk_y, −zk_z) (24,27).

Figure 3.

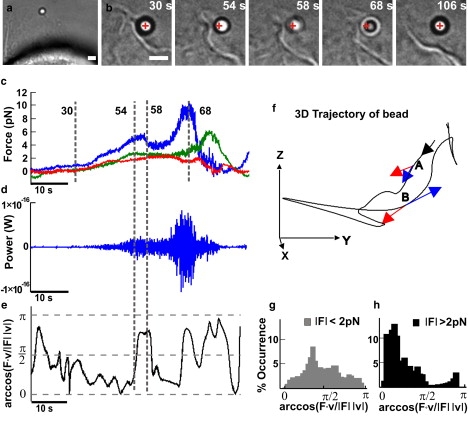
Mechanics of collisions between lamellipodia and beads. (a) Low-resolution image of a lamellipodium pushing a trapped bead. Scale bar, 2 μm. (b) Successive frames taken at different times during the push. The cross indicates the center of the optical trap. Scale bar, 2 μm. (c) The three components of the force, F_x (blue), F_y (green), and F_z (red), exerted by a lamellipodium during the push smoothed at 10 Hz. (d) Instantaneous power F·v acting on the bead. (e) Time evolution of arccos(F·v/|F| |v|) during the push. Data obtained after smoothing at 0.2 Hz. (f) The trajectory of the bead in a 3D space. The black arrow indicates the direction of the trajectory. Red and blue arrows on A and B indicate the instantaneous F and v, respectively, at the two times corresponding to 54 and 58 s in c–e. When F and v are parallel, arccos(F·v/|F| |v|) is close to 0, and when F and v are antiparallel, arccos(F·v/|F| |v|) is close to π. (g) Histogram of the arccos(F·v/|F| |v|) when |F| was <2 pN. (h) Histogram of the arccos(F·v/|F| |v|) when |F| was >2 pN.

In what follows we will compute and analyze properties of the Fv relationships for the four most common stereotyped behaviors:

• Vertical pushes (42 experiments): when lamellipodia lifted the bead upward (Fig. 2 f, 55–68.2 s) and F changed primarily along the z component (Fig. 2 g, 64-68.2 s);

• Lateral pushes (22 experiments): when lamellipodia pushed the bead laterally in the xy plane (see Fig. 5 b), whereas F changed primarily along the x and y components (see Fig. 5, c–e);

• Vertical retractions (22 experiments): when the bead was displaced vertically toward the bottom of the coverslip after bead adhesion to the growth cone membrane and lamellipodia retraction. In these cases, either the lamellipodium grew under the bead or the bead was attracted toward the lamellipodium membrane by interactions with protruding structures such as ruffles (30);

• Lateral retractions (21 experiments): when the bead was displaced laterally after adhesion to lamellipodia (Fig. 2 f, 94–123 s and Fig. 2 g, 95–110 s).

The computation of Fv relationships from measured x and F requires careful data processing, as described in Materials and Methods (see Fig. 1). Before computing Fv relationships for the four stereotyped behaviors, it is necessary to analyze in detail the mechanics of collisions between beads and lamellipodia.

Mechanics of collisions between beads and lamellipodia

When the lamellipodium leading edge (Fig. 3 a) pushed the bead (Fig. 3 b), F_x, F_y, and F_z often change almost independently, reaching their maximum amplitude at different times (Fig. 3 c). In these cases, the bead moves along a trajectory that often changes its direction (Fig. 3 f, black trace). To investigate quantitatively the nature of these events, it is useful to monitor the vectors F and v, with their modulus and direction. The power dissipated by the lamellipodium is the scalar product F · v. The amplitude of the instantaneous velocity depends on the bandwidth used for filtering the data, and F · v reaches values up to 2.5 × 10⁻¹⁸ W when v is computed at a bandwidth of 0.2 Hz, but up to 10⁻¹⁶ W at a bandwidth up to 10 Hz (Fig. 3 d). The analysis of the angle ϕ between F and v provides information useful for understanding the mechanics of collision between beads and lamellipodia: when ϕ is close to 0 the lamellipodium pushes the bead and performs a positive work, and when ϕ is close to π, the lamellipodium retracts. When ϕ is close to π/2, lamellipodia do not carry out any work. A negligible work is performed primarily in two cases: first, when the lamellipodium exerts a force comparable to that caused by Brownian collisions with water molecules; and second, when the bead slides over the lamellipodium, F becomes orthogonal to v, and no work is done. The angle ϕ was determined by arccos(F · v/|F| |v|) (Fig. 3 e). When the modulus of F was >2 pN, ϕ was usually close to either 0 or π (Fig. 3 h), indicating that F and v have the same or opposite direction.

In contrast, when the modulus of F is <2 pN (Fig. 3 g), the value of ϕ is usually close to π/2. A sudden change of the bead motion (as shown in Fig. 3 f) could be caused either by a momentary sliding of the bead over the lamellipodium or by a transient retraction of the lamellipodium leading edge. The position of the lamellipodium was followed by video imaging with a CCD camera (see Fig. 3, a and b), and we could verify by visual inspection that the bead was always in contact with the lamellipodium leading edge. In addition, these two mechanisms can be easily distinguished by observing the work done: if the bead slides over the lamellipodium, no work is done and ϕ remains close to π/2. If, instead, the lamellipodium transiently retracts, the work done by the lamellipodium is negative, and ϕ remains close to π. Using this procedure, we verified that periods with negative velocity analyzed in Figs. 3–6, were indeed associated with values of ϕ close to π and that therefore they were not caused by an occasional sliding of the bead but by transient retractions of the lamellipodium leading edge.

During pushes, Fv relationships are flat only on average and growth alternates with transient retractions

When lamellipodia pushed the bead upward, they exerted forces up to 20 pN, and often only the F_z component of the force changed (Fig. 2 g, 64–68.2 s). In 5 of 42 vertical pushes, as in the experiment illustrated in Fig. 2 g, when the bead displacement was low-pass filtered at 0.2 Hz (Fig. 4 a, green trace), corresponding to a temporal averaging over a time window of 3–5 s, the computed velocity, v_{z push}, had little oscillations around an almost constant value. The obtained Fv relationship (Fig. 4 b, green trace), after an initial rise, was almost flat, indicating that the lamellipodium can increase the exerted force while lifting the bead away from the surface with an almost constant velocity. Nearly identical results were obtained when Fv relationships were computed from the modulus of F and not from a single component (F_z).

In 37 of 42 experiments, the Fv relationships exhibited transient periods where the velocity oscillated and could even reverse its direction, leading to the appearance of loops in Fv relationships (Fig. 4, c and d). We computed Fv relationships from the experiment of Fig. 4 a after smoothing at 0.2 (Fig. 4 b, green trace), 1 (Fig. 4 b, pink trace), and 10 Hz (Fig. 4 c). When data were smoothed at 1 and 10 Hz, the velocity oscillated around a constant value of ∼60 nm/s, reaching occasional peak values from 0.12 (Fig. 4 b, pink trace) to 3 μm/s (Fig. 4 c), respectively.

The Fv relationships from individual experiments were normalized to F_max, defined as the maximal force beyond which the lamellipodium leading edge does not advance and the velocity is consistently negative for at least 10 s. Normalized Fv relationships, even those obtained from data filtered at 0.2 Hz, varied significantly in different experiments (Fig. 4 d), suggesting that force generation is not a deterministic but a probabilistic process. To characterize the underlying probabilistic dynamics, we determined average Fv relationships, <Fv>, in vertical pushes for data filtered at 0.2, 1, and 10 Hz. The three average Fv relationships exhibited the same overall behavior (Fig. 4 e), with the velocity increasing together with the force, up to ∼65 nm/s, and remaining approximately constant up to F_max. Therefore, the <Fv> for vertical pushes is flat.

In some experiments, the lamellipodium (Fig. 5 a) caused a pure lateral displacement (Fig. 5 b) so that only F_x and F_y changed appreciably (Fig. 5, c and d), whereas F_z remained constant (Fig. 5 e). In Fv relationships computed from these lateral pushes (Fig. 5 f), clear loops were detected, as observed in vertical pushes (Fig. 4, c and d).

The number of loops in the Fv relationships computed for both the F_x and F_y components increased when the bandwidth of Gaussian filtering increased from 0.2 to 1 Hz (Fig. 5 f, green and pink traces, respectively). As in the case of the vertical push, normalized Fv relationships for lateral pushes in individual experiments were different. <Fv> relationships for lateral pushes filtered at 0.2, 1, and 10 Hz (Fig. 5 g) exhibited the same overall behavior, with a mean velocity of ∼15 nm/s. As illustrated in the 3D representation of Fig. 2 d, a thin lamellipodium can grow under the bead without displacing it (see also Fig. S2); therefore, the measured mean velocity during lateral pushes could be lower than that for vertical pushes (65 nm/s) because fast lateral pushes of thin lamellipodia could not be measured.

Fv relationships during retractions

Molecular mechanisms underlying both vertical and lateral pushes primarily involve actin filament polymerization, and it is not surprising that <Fv> relationships for vertical and lateral pushes have a similar shape (compare Figs. 4 e and 5 g), but a different dynamics could be expected when the bead is pulled by a lamellipodium. Therefore, we computed <Fv> relationships during vertical and lateral retractions.

Individual normalized Fv relationships obtained during lateral and vertical retractions (Fig. 6, a and c) varied in different experiments. In 22 out of 22 vertical retractions, when data were filtered at 0.2 Hz, the velocity was consistently negative and did not change its direction. In contrast, during lateral retractions, the velocity transiently reversed its direction in 3 out of 21 experiments. <Fv> relationships for retractions (Fig. 6, b and d) exhibited the same overall behavior, but with a mean velocity of about −15 and −35 nm/s for lateral and vertical retractions, respectively. Having observed that the lamellipodium leading edge could invert its velocity direction, we asked whether these transient inversions of the velocity had different properties during pushes and retractions, and whether they occurred more frequently near the maximal measured force, F_max. When data were filtered at 0.2 Hz, transient inversions of the velocity were evident for vertical and lateral pushes and for lateral retractions but completely absent for vertical retractions (Fig. 6 c). In contrast, at a bandwidth of 10 Hz, transient inversions were observed for vertical and lateral pushes and retractions (data not shown). The occurrence of a transient inversion of the velocity depends smoothly on F/F_max (Fig. 4 d), indicating that transient retractions are not triggered by a strong load but originate from a random process.

Discussion

This study provides a precise characterization of force generation in DRG lamellipodia with millisecond time resolution and picoNewton sensitivity. Previous measurements made with the cantilever of an AFM were restricted to a temporal resolution in the second range and were obtained in migrating keratocytes producing forces in the nN range (22). Using optical tweezers, we measured force generation in DRG growth cones, and we could characterize several physical properties of the molecular network underlying force generation. As shown in Fig. 1 a (see Materials and Methods), relevant biological events occur on a timescale of <100 ms, and different dynamical properties are seen at a timescale of 3–5 s. Our results show that i), force generation is not a deterministic mechanism but follows a probabilistic process; ii), underlying dynamical events occur on different timescales varying from 100 ms to 5 s; iii), fast growths alternate with local retractions of the lamellipodium leading edge. These results give new insight on dynamical properties of force generation in neuronal growth cone lamellipodia and the biochemical network controlling them (10,31,32).

Physical properties of force generation

The maximal force exerted by lamellipodia pushing on a bead with a diameter of 1 μm was ∼20 pN (25). In some experiments, this force clearly stopped the lamellipodium growth and could be identified as the stall force, F_stall, i.e., the force capable of blocking protrusion. As lamellipodia very often retract spontaneously, in most experiments, F_stall is expected to be larger than the measured maximum force, F_max. The contact area between pushing lamellipodia and beads was determined by the analysis of video images of the event under examination. For all frames i corresponding to a detectable force measured with the QPD, we determined the arc Γ_i of the bead in close contact with the leading edge of the lamellipodium and the corresponding angle 2θ_i on the bead center (Fig. 7, a–c, red).

Figure 7.

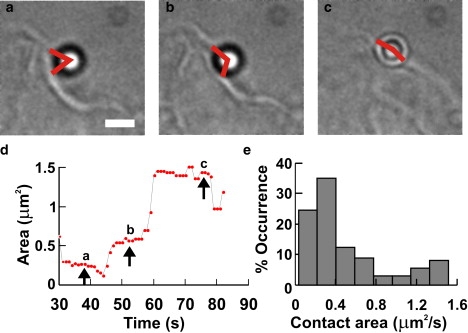
Contact area between a pushing lamellpodium and the bead. (a–c) Micrographs of a lamellipodium pushing the bead at different times (see timescale in d). Scale bar, 2 μm. Red angles drawn by eye. (d) Time evolution of estimated contact area, S_c, during the push. (e) Histograms of the value of S_c obtained from four experiments during which a lamellipodium pushed the bead.

Then the contact surface at frame i, S_c(i), is assumed to be equal to the corresponding spherical cap of the bead. Simple geometrical formulae indicate that S_c(i) = 2π(1 − cosθ_i)r², where r is the bead radius. Fig. 7 d reproduces the time evolution of the estimated value of S_c when a lamellipodium pushed a bead. The value of S_c varied from 0.25 to 1.57 μm² (Fig. 7 e). Therefore, the maximal pressure exerted by DRG lamellipodia was 20–80 pN/μm². The maximum power/unit area exerted by lamellipodia was calculated to be 1-4 × 10⁻¹⁶ W/μm². Hydrolysis of one molecule of ATP provides energy of ∼10⁻¹⁹ J (33), and if this energy is converted into work with an efficiency of 60%, the hydrolysis of ∼0.25–1 × 10⁴ s⁻¹ of ATP molecules/μm² is necessary to produce the measured power. The number of actin filaments in keratocyte and fibroblast lamellipodia has been estimated to be of the order of 100/μm² (22). Therefore, the number of elementary motors/μm² is likely to be of the order of 100, where each elementary motor consumes ∼25–100 ATP molecules/s. These numbers should be compared with measurements obtained in the analysis undertaken in this study. One actin monomer is ∼2 nm long, and if the consumption of one ATP is necessary for the addition of one actin monomer, actin filaments will grow at a velocity of 50–200 nm/s, very similar to the velocity of vertically pushing lamellipodia (Fig. 4). When these filaments elongate, the net protrusive force exerted across the membrane depends on a number of factors; in fact, when an actin monomer is added to an actin filament, an increase of the protrusive force depends on the angle between the filament and the membrane and on the rigidity of the membrane itself. Moreover, the observation that the load force necessary to stall the growth of a bundle of actin filaments is very similar to that for a single actin filament (34) indicates that the addition of actin monomers into nearby filaments does not necessarily lead to a linear summation of the protrusive force exerted by the polymerization of a single filament. As these factors could vary in different cells, it is not surprising that F_stall in DRG lamellipodia, here reported, is smaller than the value of 2 nN observed in migrating keratocytes (22). In migrating keratocytes, the hydrodynamic load generated by a fluid flow producing an opposing force of just some pN/μm² arrests the forward movement of lamellipodia, suggesting that measurements of protrusive force at the leading edge are difficult to interpret because of the interplay between protrusion and adhesion (35).

The measure with optical tweezers here reported underestimates the velocity of protruding lamellipodia. The center of the bead is usually trapped at a distance varying from 600 to 900 nm from the underlying coverslip; as the radius of the bead is 500 nm, the height of the free space under the bead is between 100 and 400 nm. The height of protruding lamellipodia varies between 45 and 660 nm (Fig. 2 b), and thin lamellipodia therefore can grow below the bead without pushing it. This is the situation of many fast growing lamellipodia and is illustrated in Fig. S2 a, which shows a lamellipodium growing under the bead. In this experiment, and in several other cases, no significant bead displacement was measured (Fig. S2 b). We compared the maximal lateral velocity—obtained by the analysis of image sequences—in the same sample: the measured maximal lateral velocity of 15 thin protruding lamellipodia was 30 ± 22 nm/s and the same quantity for lamellipodia displacing a bead trapped in front of them was 15 ± 3 nm/s. The difference is ascribed to the larger protruding velocity of thin lamellipodia and the action of the bead-stalling protrusion. Therefore measured velocities in Fv relationships here reported are underestimated.

Fv relationships

Fv relationships were computed for vertical (Fig. 4) and lateral pushes (Fig. 5) and for vertical and lateral retractions (Fig. 6). In all these cases, <Fv> relationships exhibited a flat shape, during which the mean velocity remained constant while the force increased. The mean velocity for vertical pushes and retractions was 65 and 35 nm/s respectively. Vertical pushes were usually faster than lateral pushes. However, the lower measured mean velocity for lateral pushes could be caused by an experimental limitation of our measuring system: as illustrated in Fig. 2 d and Fig. S2, a fast-advancing lamellipodium with a height of <150 nm could grow under the bead without displacing it.

When position and force were filtered at 0.2 Hz, in some experiments, pushing lamellipodia exerted increasing force while maintaining a constant velocity (Fig. 4 b). In the great majority of the experiments performed, however, force generation was characterized by large fluctuations of the velocity. This observation shows that force generation in lamellipodia is probabilistic in nature and that only <Fv> relationships (Fig. 4 e) exhibit a flat shape, during which the mean velocity remains constant while the force can increase. Therefore, autocatalytic models correctly describe force generation only in a mean approximation. In individual experiments, the velocity does not remain constant but oscillates and can change its direction. During these events, the actin filaments network retracts, possibly due to local catastrophe or organized depolymerization controlled by cofilin and other severing proteins (10). Therefore, force generation is not a smooth process but is characterized by a random alternation of fast growths and retractions of the lamellipodium leading edge.

Possible mechanisms underlying transient inversions

What could be the mechanism underlying the unstable dynamics responsible for transient inversions of the velocity during growth and retraction? Several mechanisms could contribute to measured transient inversions of the velocity. In many experiments, we observed a combination of vertical and lateral pushes in which the bead could detach transiently from the lamellipodium leading edge. In our analysis, we carefully selected and analyzed pure lateral pushes during which we did not detect any vertical displacement. Indeed, in the experiment illustrated in Fig. 5, we did not measure any concomitant vertical shift at the time of the velocity reversal. In the reported Fv relationships there was no significant correlation between lateral and vertical bead movement at the times of velocity reversal.

It is also possible that the bead slides locally on the lamellipodium surface because of an improper “cupping” around the bead and because of local inhomogeneity of the cell membrane. In several of the experiments where transient inversions of the velocity were measured, we observed a strong adhesion of the bead to the lamellipodium membrane. In these experiments, the bead remained sealed on the leading edge and when the lamellipodium retracted the bead was pulled away from the optical trap (Fig. 2 f, 102 s). The possibility of local sliding is also addressed in Fig. 3. By analyzing the angle between the measured F and v, we could rule out a possible local sliding of the bead at the time of the velocity reversal. In these conditions, movements of the bead are likely to be caused primarily by movements of the actin network operating behind the membrane.

As shown in Figs. 4 and 5, transient inversions of the velocity are more frequent during pushes than when the lamellipodia retract (Fig. 6). This observation suggests that different dynamics control push and retraction. During pushes, proteins controlling the network of actin filaments, such as cofilin, could randomly sever a large branch of actin filaments, leading to a local catastrophe and causing a transient retraction of the lamellipodium leading edge. When lamellipodia retract, a more global catastrophe of the network of actin filaments is likely to occur.

Although the occurrence of local catastrophes seems the most likely mechanism underlying local transient retractions, the complexity of biological events underlying force generation suggests a multiple origin of the observed events. Indeed, transient retractions could also be caused by the retrograde actin flow and contraction of myosin II (36,37). The driving force behind retrograde flow of actin originates from myosin II contractility and “push” of the plus-end of actin assembly at the lamellipodium leading edge (38). It is possible that a sudden increase of retrograde flow of actin and/or a burst of myosin II contractility, accompanied by lack of firm attachment to the coverslip, lead to a transient retraction of the lamellipodium leading edge.

Also, the mechanical interaction between the cellular membrane and the network of actin filaments could give rise to transient retractions. Growing and branching of the actin filaments can become unstable due to resistance from membrane tension. Indeed, the maximum measured force, F_max, is ∼20–100 pN/μm², of the same order as the force exerted by a membrane with a surface tension, γ, equal to 0.005 k_BT/nm² axially deformed by 1 μm (39). The actin filament network is confronted with a membrane exerting a force similar to F_max, so that the actin filament network is only marginally stable and its propulsive force is almost counterbalanced by the membrane tension. Growing and retracting in conditions of marginal stability allows fast reactions and could provide lamellipodia with the flexibility necessary for their physiological functions.

The Fv relationships reported here were obtained in intact neurons where protrusion and retraction are controlled by a sophisticated machinery, and it is somehow surprising that average Fv relationships, <Fv>, are simple (Figs. 4–6).