Abstract
Using the harmonic-approximation approach of the accompanying paper and AM1 energy surfaces of terminally-blocked amino-acid residues, we determined physics-based side-chain-rotamer potentials and the side-chain virtual-bond-deformation potentials of 19 natural amino-acid residues with side chains. The potentials were approximated by analytical formulas and implemented in the UNRES mesoscopic dynamics program. For comparison, the corresponding statistical potentials were determined from 19,682 high-resolution protein structures. The low-free-energy region of both the AM1-derived and the statistical potentials is determined by the valence geometry and the L-chirality, and its size increases with side-chain flexibility and decreases with increasing virtual-bond-angle θ. The differences between the free energies of rotamers are greater for the AM1-derived potentials compared to the statistical potentials and, for alanine and other residues with small side chains, a region corresponding to the conformation has remarkably low free energy for the AM1-derived potentials, as opposed to the statistical potentials. These differences probably result from the interactions between neighboring residues and indicate the need for introduction of cooperative terms accounting for the coupling between side-chain-rotamer and backbone interactions. Both AM1-derived and statistical virtual-bond-deformation potentials are multimodal for flexible side chains and are topologically similar; however, the regions of minima of the statistical potentials are much narrower, which probably results from imposing restraints in structure determination. The force field with the new potentials was preliminarily optimized using the FBP WW domain (1E0L) and the engrailed homeodomain (1ENH) as training proteins and assessed to be reasonably transferable.
Keywords: protein folding, UNRES force field, local-interaction potentials, molecular quantum mechanics, harmonic approximation
1 Introduction
In the accompanying paper,1 we described the theory of our recently developed method to compute the potentials of mean force for the rotameric states and those for the deformation of the virtual bonds of the united side chains as functions of their location with respect to the frames (for the united side chain connected to ). We used the AM1 semiempirical method of molecular quantum mechanics2 to compute non-adiabatic energy surfaces of two sample terminally-blocked amino-acid residues, alanine and valine (where the energy was minimized with respect to all degrees of freedom except the angles λ(1) and λ(2) for rotation about the Cα ⋯ Cα virtual-bond axes and the χ angles of the side chains corresponding to the rotation of non-hydrogen atoms; the λ(1), λ(2), and χ angles formed a multidimensional grid). Use of a harmonic approximation enabled us to estimate the energy values outside the grid points and, consequently, to compute statistical sums over the sections of the energy surface corresponding to a given local geometry of a triad plus the ith side-chain center (SCi). By comparing the PMF's computed by using our harmonic approximation with those obtained by direct Monte Carlo integration over the AM1 energy surfaces for alanine and valine, we found that the harmonic-approximation PMF surfaces are more structured than the Monte Carlo surfaces but preserve their essential features, while using the Monte Carlo method to compute the PMF surfaces of all 19 natural amino-acid residues which possess side chains would be too expensive. Consequently, in this work, we apply the AM1 semiempirical method2 and the harmonic approximation to compute the side-chain rotamer and virtual-bond-deformation potentials of these 19 residues. Subsequently, we fitted analytical formulas to the potentials of mean force and incorporated the new potentials into UNRES. We also compared the determined potentials of mean force with the respective knowledge-based potentials determined from the structures in the Protein Data Bank (PDB).3
This paper is organized as follows. In section 2, we describe the procedure for calculating the energy surfaces, the analytical formulas for the potentials, and the fitting procedure. In section 3.1, we discuss briefly the resulting side-chain-rotamer potentials, compare them with the statistics-based PMF's derived from the PDB, and discuss the quality of fitting the PMF's with analytical functions; the same discussion of the virtual-bond-deformation potentials is presented in section 3.2. In section 3.3, we present preliminary results of optimization of the force field with the new potentials as well as the new virtual-bond-angle bending potentials determined in our recent work4 using two proteins: the engrailed homeodomain (PDB code: 1ENH; an α-helical protein) and the FBP-28 WW domain (PDB code: 1E0L; a 37-residue β-protein). In section 3.4, we demonstrate how the new potentials improved the stability of our mesoscopic MD algorithm5 compared to the use of the knowledge-based potentials. Finally, in section 4 we recapitulate the results and discuss possible future extension of the treatment of interactions involving side-chain-rotamer states in the UNRES model.
2 Methods
2.1 Calculation of the side-chain-rotamer and virtual-bond-deformation potentials
The UNRES force field is described in detail in our earlier work4, 6-15 and also recapitulated in the accompanying paper.1 As stated in the accompanying paper,1 the potentials of mean force of the rotameric states of the united side chain of type X, FX(θ, r̂SC), are functions of the Cartesian coordinates of the unit vector of a side chain in a local coordinate system based on three consecutive Cα atoms (r̂SC) and the corresponding virtual-bond-valence angle θ (Figure 1). The rotamer-energy contribution to the UNRES force field, Urot(θ, r̂SC) is obtained from FX(θ, r̂SC) by subtracting the potential of mean force corresponding to the virtual-bond-angle bending, F̄X′(θ) [see eq. (6) of the accompanying paper]. The virtual-bond-deformation potentials, Ubond(bSC), are defined as potentials of mean force dependent on the virtual-bond length bSC of a given side chain. The theory for computing the potentials of mean force, mentioned above, from the sections of the non-adiabatic energy surfaces of terminally-blocked amino-acid residues with the use of a harmonic approximation to estimate the energy values outside the grid points, is presented in the accompanying paper.1 The energy surfaces are expressed in the angles of rotation of the peptide groups about the virtual-bond Cα ⋯ Cα axes λ(1) and λ(2) (defined in reference 16 and also shown in Figure 2a of the accompanying paper) and in the angles of rotation about the side-chain bonds, χ1, χ2, …, χn (where n is the number of rotatable bonds in a side chain).
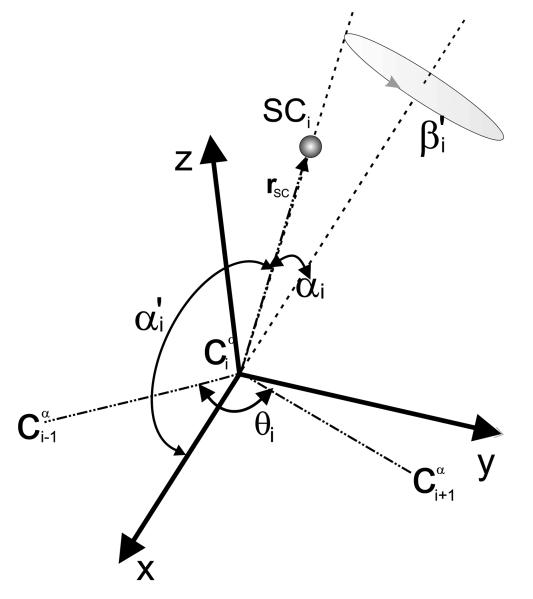
Fig. 1.
Illustration of the local coordinate system of a virtual-bond side chain. Dot-dashed lines indicate the virtual bonds. The atom is at the origin of the reference system, the x axis of the reference system is the bisector of the virtual-bond angle θ, the y axis lies in the plane of the three Cα atoms, is perpendicular to the x axis and directed from to . All three axes (x, y, and z) form a right-handed reference system. rSC is the vector pointing from to the geometric center of the side chain. The angle α′ is the planar angle between the bisector of the θ angle and the Cα ⋯ SC vector and the angle β′ is the angle of clockwise rotation of the Cα ⋯ SC virtual-bond axis about the bisector of the θ angle from the plane of the three Cα atoms, taking the position of SC in the plane closer to (with positive y) as reference (β′ = 0°).
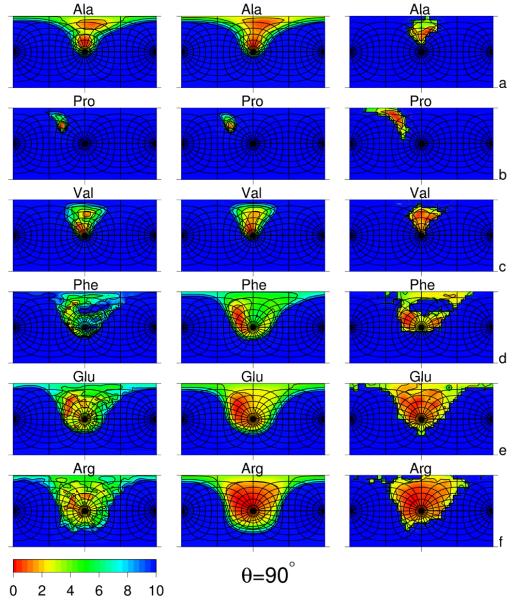
Fig. 2.
Side-chain-rotamer potential surfaces plotted in the angles α′ and β′ (cf. Figure 1) of selected amino-acid residues: Ala (a), Pro (b), Val (c), Phe (d), Glu (e), and Arg (f) computed from the respective non-adiabatic AM1 energy surfaces, using the harmonic-approximation procedure described in the accompanying paper1 (left panels), fitted to the AM1-derived surfaces using eq. (3) (middle panels), and derived from the PDB as statistical potentials (right panels) for the virtual-bond-valence angle θ = 90°. The “South Pole” (α′ = 180°) is the point in the center of each panel, and the “North Pole” (α′ = 0°) is in the middle of the left and of the right vertical side of the rectangle. The parallels (lines of constant α′) are the distorted circles centered about the “South Pole” (except the parallel corresponding to α′ = 90°, which is a square centered at the “South Pole”) and semicircles centered about the “North Pole”, except those corresponding to α′ = 90° (the “Equator”) which constitute two half-squares. The meridians are the lines intersecting the parallels and running between the “North Pole” and the “South Pole”. The parallels and the meridians are each spaced 15°. The horizontal half-line going from the center of each panel to the right corresponds to β′ = 0° and that going from the center to the left corresponds to β′ = 180°; β′ increases when rotating clockwise about the “South Pole”. For all residues, the data to calculate the statistical potentials were taken from residues not involved in regular secondary structures. The free-energy color scale is shown in the small left-bottom panel.
To evaluate FX(θ, r̂SC), we computed the energy surfaces of all natural terminally-blocked L-amino-acid residues as functions of λ(1), λ(2), and the χ angles involving non-hydrogen atoms by using the AM1 semiempirical method;2 these χ angles will later be referred to as the significant χ angles (thus, there is no significant χ angle for the alanine residue, there is one for cysteine, valine, and serine, etc.). The side chains of aspartic acid, glutamic acid, arginine, and lysine were taken in the neutral state to avoid overemphasizing electrostatic interactions of the side chains with the peptide backbone, which would arise because of not considering the electrostatic interactions with the solvent. Use of the ab initio approach was prohibitively expensive and it was found in earlier works11, 17 that the AM1 method gives qualitatively similar energy surfaces of terminally-blocked glycine, alanine, and proline to those computed with the ab initio method. Glycine was not considered, because it does not have a side chain. The grid sizes of dihedral-angle scanning and the numbers of grid points of the 19 natural amino-acid residues which possess a side chain are summarized in Table 1. For each grid point, a starting conformation was constructed based on the standard valence geometry; the conformation was subsequently energy-minimized in all internal coordinates except for the grid variables (λ(1), λ(2), χ1, χ2, ⋯, χn). After minimization, the energy Hessian was computed to enable us to use the harmonic approximation to compute the PMF's. We used the MOPAC'9318 program to carry out these calculations.
Table 1.
Grid sizes in λ(1), λ(2), the significant χ angles (involving rotation of non-hydrogen atoms), and the numbers of grid points for the 19 natural amino-acid residues with side chains (glycine is excluded because it does not have a side chain). The amino-acid residues are grouped according to the number of significant χ angles.
| Grid size (degrees) |
||||||||
|---|---|---|---|---|---|---|---|---|
| n χ a | λ (1) | λ (2) | χ 1 | χ 2 | χ 3 | χ 4 | Residue(s) | Ngridb |
| 0 | – | 30 | – | – | – | – | Pro | 12 |
| 30 | 30 | – | – | – | – | Ala | 144 | |
|
| ||||||||
| 1 | 30 | 30 | 30 | – | – | – | Cys, Ser, Thr, Val | 1728 |
|
| ||||||||
| 2 | 30 | 30 | 30 | 30 | – | – | Asn, Asp, His, Ile, Leu, Phe, Trp, Tyr | 20736 |
|
| ||||||||
| 3 | 30 | 30 | 30 | 30 | 60 | – | Glu, Gln, Met | 124416 |
|
| ||||||||
| 4 | 30 | 30 | 30 | 60 | 120 | 120 | Arg, Lys | 93312 |
Number of significant χ angles.
Number of grid points.
2.2 Determination of statistical side-chain-rotamer and virtual-bond potentials
In order to assess how the side-chain-rotamer PMF's determined from the AM1 energy surfaces of terminally-blocked amino-acid residues differ from the respective statistical potentials, we determined the statistical potentials from the PDB structures. We took 19,682 protein structures from the PDB, 14,454 of which were X-ray structures with resolution 2 Å or less and 5,228 were NMR structures. The full list of the proteins is in Table S1 of the Supplementary Material. To obtain statistical potentials as free as possible from the context of the protein structure, we considered only the residues not involved in secondary structure (helices and sheets). However, we observed little differences between the statistical rotamer potentials corresponding to residues in regular secondary structures and those outside them, respectively, and almost no differences between the statistical virtual-bond-deformation potentials obtained from residues in and outside regular secondary structures, respectively.
We collected three-dimensional histograms in the angles α′, β′, and θ, defining the orientation of a Cα ⋯ SC vector with respect to the frame of three consecutive Cαs (see Figure 1, and also Figures 1 and 2 of the accompanying paper), and one-dimensional distributions of the Cα ⋯ SC distances. Then, for a side chain of type X, the rotamer [Wrot(α′, β′, θ)] and virtual-bond-deformation [Wbond(d)] statistical potentials were calculated from eqs. (1) and (2), respectively.
| (1) |
where H(α′, β′, θ) is the normalized histogram at a given triple of angles α′, β′, and θ. The grid in α′, β′, and θ was 10°, R is the universal gas constant and T is the absolute temperature; we assumed T = 298°K. The histogram value in eq. (1) is divided by sin α′ because the surface element in polar coordinates is equal to dS = sin α′dα′dβ′.
| (2) |
where H(d) is the normalized histogram at virtual-bond length d; the grid was 0.01 Å.
2.3 Fitting analytical formulas to the AM1-derived potentials of mean force
The energy of a side chain interacting with two neighboring peptide groups (Figure 1, and also Figure 2 of the accompanying paper) depends primarily on the van der Waals interactions between the atoms of the peptide-group centers and those of the side chain. Consequently, the simplest functional form could be composed of and , where d̄SCp1 and d̄SCp2 denote the average distance of the side-chain atom from the atoms of the peptide group between and or those between and , respectively, plus some simple harmonic terms to account for the deformation of the real valence angles. These average distances could be approximated by the distances between the UNRES side-chain center and the peptide (p) centers connected to . However, such a simple formula does not capture the complexity of the PMF surfaces of the side chains of terminally-blocked amino-acid residues. Therefore, we assumed a more complex functional form which includes inverse powers of d̄SCp1 and d̄SCp2 and polynomials in the coordinates of r̂SC. The functional form of Urot(θ, r̂SC) assumed in this work is expressed by eq. (3).
| (3) |
where (r̂1, r̂2, r̂3) are the Cartesian coordinates of r̂SC; the a′s, b′s, and c′s, as well as μ1, μ2, ε1, and ε2 are adjustable parameters, and d̄SCp1 and d̄SCp2 have the sense of average distances of the atoms of the first and the second peptide group, respectively, from the atoms of the respective side chain; they are computed from eqs. (4) and (5), respectively.
| (4) |
| (5) |
| (6) |
| (7) |
where d̄SC, d̄p/2, can be considered as average distances of the atoms of the side chain, and of the first or the second peptide group, respectively, from the origin of the local coordinate system (see Figure 1); however, the corresponding adjustable parameters, δp/2 and δSC are shifts of these distances from the midpoint between Cα and Cβ and that between the two consecutive Cα atoms, respectively, as defined by eqs. (6) and (7). The constant 0.1 has been introduced in the denominators of the expressions containing d̄SCp1, , d̄SCp2, and in eq. (3) to avoid problems with very small d′s in fitting.
For the virtual-bond-deformation potentials, which turned out to be multimodal for complex side chains, we assumed a Padé-like functional form, as expressed by eq. (8)
| (8) |
where the a′s, b°′s, and k′s are the adjustable parameters; the b°′s and k′s have the meaning of “unstrained” bond lengths and force constants corresponding to given series of rotamers of a side chain, and n is the number of terms in the expression. For n = 1, eq. (8) is reduced to a conventional harmonic expression.
We used the Levenberg-Marquardt method19 to fit the analytical expressions for Urot and Ubond to the respective potentials of mean force. For each side chain, we tried several sets of starting parameters, as well as starting from simpler functional forms and subsequently adding the next terms, to achieve the best fit.
2.4 Optimization of the force field
To introduce the new Urot and Ubond, as well as Ub potentials determined in our earlier work4 with UNRES, we used the hierarchical optimization method described in our earlier work10, 13, 20 and recently extended to optimization of force fields for canonical simulations.14 In this method, the force-field parameters are tuned to achieve foldability of the force field for one or more selected training proteins. The idea of the hierarchical approach is that partially-folded structures have free energies ordered according to the degree of native-likeness,10 understood in a discrete manner as the presence of given secondary-structure elements and, further, their packing. Each set of conformations with the same discrete degree of native-likeliness is termed a level. As a result of optimization, the free-energy differences between levels approach those found experimentally for the training proteins (if such data are available) or, at least, the target free-energy relations are established qualitatively so that the native-like level has the lowest free energy below the folding-transition temperature, the free energy of the native-like level equals the cumulative free energy of all other levels at the folding-transition temperature, and the native-like level is the highest in free energy above the folding-transition temperature.14
We optimized the UNRES force field with temperature-dependent terms corresponding to the cluster-cumulant factors of order greater than 2, as introduced in our recent work.14 The optimized parameters were energy-term weights with initial values taken from values optimized using the 1GAB protein in our recent work,14 the well-depths of the Gay-Berne potential for which the values determined from the PDB6 were taken as the initial values, and the coefficients of the second-order two-dimensional Fourier expansion of the local-interaction energy surfaces of terminally-blocked glycine, alanine, and proline, for which the values optimized in our earlier work13 were taken as initial values.
We used two training proteins: the engrailed homeodomain (a three-helix bundle; PDB code: 1ENH21) and the FBP WW domain (a three-stranded antiparallel β-sheet; PDB code: 1E0L22). The experimental free-energy profile of folding of 1E0L determined by fluorescence spectroscopy by Nguyen et al.23 was used, while the free-energy profile of folding of 1ENH was calculated by integration of the heat-capacity curve determined by Mayor et al.24 The target function in optimization and the optimization procedure were those described in our earlier work14 except that, for 1ENH, we added an additional term, containing the difference between the ensemble-averaged radius of gyration and the expected value of this quantity in the folded and in the unfolded state, to the optimized target function. This prevented the optimized energy function from producing collapsed structures at temperatures above the folding-transition temperatures. For the unfolded 1ENH, we took the experimental value (20 Å)24 of the radius of gyration. For the folded 1ENH, we took the radius of gyration calculated from the coordinates of the respective NMR structure, which was 10 Å. There are no experimental data on the radius of gyration of unfolded 1E0L but we assumed that inclusion of the data of one protein would suffice to prevent the energy function from producing over-collapsed unfolded structures. The multiplexed replica exchange (MREMD) method,25 which we recently implemented for UNRES,26, 27 was applied to generate decoy sets. We ran 2 replicas per temperature at 32 temperatures from T = 250 K to T = 500 K (a total of 64 replicas). The results were subsequently processed with the weighted histogram analysis method (WHAM)28 to compute ensemble-averaged quantities, as described in our earlier work.14
3 Results and Discussion
3.1 Side-chain-rotamer potentials
The maps of Urot computed from the AM1 energy surfaces, the fitted analytical potentials [eq. (3)], and the corresponding statistical potentials [eq. (1)], of six selected amino-acid residue types (Ala, Pro, Val, Phe, Glu and Arg) obtained for θ = 90° and θ = 140°, respectively, are shown in Figure 2 and Figure 3, respectively. The residue types were selected based on the number of significant χ angles considered in this work (from 0 to 4; see Table 1); additionally, proline was selected because of its great rigidity caused by the presence of a covalent link between the backbone and the side chain. Similar plots for all 19 amino-acid residues are presented in Figures S1 and S2 of the Supplementary Material. The coefficients of eqs. (3 - 7) are shown in Table S2 of Supplementary Material.
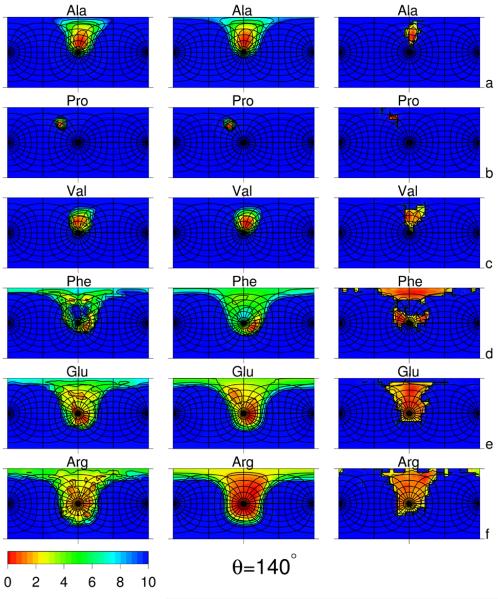
Fig. 3.
Side-chain-rotamers potential surfaces plotted in angles α′ and β′ (cf. Figure 1) of selected amino-acid residues: Ala (a), Pro (b), Val (c), Phe (d), Glu (e), and Arg (f) for virtual-bond-angle θ = 140°. See Figure 2 for detailed description. The data to calculate the statistical potentials were taken from residues not involved in regular secondary structures except proline for which all data were taken because of the small number of proline residues with θ ≈ 140°.
The following four general features of all rotamer-potential surfaces, regardless of the method of derivation (AM1 or statistical), can be pointed out:
The “northern hemisphere” (0 < α′ < 90°) except the neighborhood of the “Equator” is almost inaccessible. This is understandable, because small α′ angles correspond to side-chain atoms overlapping with the backbone peptide groups (e.g., as in the conformation for L-amino-acid residues with side chains larger than those of alanine, serine, and threonine).
The low-energy regions (located in the “southern hemisphere”) are shifted towards negative β′ angles; this feature results from the L-chirality of the natural amino-acid residues. Residues with small side chains (e.g., Ala and Val) populate the region with negative β′ almost exclusively, while those with large and flexible side chains (e.g., Arg) also populate regions with positive β′ around the “South Pole” (α′ = 180°).
The spread of the low-PMF region depends on the number of χ angles; it is narrowest for Ala which has no χ angles for which non-hydrogen atoms at the end of the side chain rotate, and it is very broad for arginine, which has four χ angles for which heavy side-chain atoms rotate. Additionally, the rotamers of proline are confined to a very narrow region centered at α′ = 105°, β′ = −150° because of a covalent constraint.
The low-PMF region becomes narrower when θ increases from 90° to 140°; this is because the position of the Cβ atom depends on the angles λ(1) and λ(2) more weakly with increasing values of θ.
The AM1-computed Urot surfaces of valine (Figure 2c and 3c; left panels), phenylalanine (Figure 2d and Figure 3d; left panels), glutamic acid (Figure 2e and Figure 3e; left panels), and arginine (Figure 2f and Figure 3f; left panels), as well as those of all residues with at least one χ angle governing the motion of non-hydrogen atoms (see the left panels of Figures S1 and S2 of Supplementary Material), contain many submaxima and subminima within the major minimum basins. As we concluded in the accompanying paper,1 this substructure is likely to be an artifact of applying the harmonic approximation to estimate energies outside the computed non-adiabatic AM1 energy surfaces. This assumption is supported by the fact that the respective statistical potentials (Figure 2 d – f and Figure 3 d – f, right panels) are smoother than those obtained from our procedure of grid summation over AM1 energy surfaces aided by use of the harmonic approximation (see the accompanying paper). As shown in Figure 2 and 3, the substructure disappears in the fitted analytical approximations to the Urot surfaces, preserving the basins of the major minima. Fitting the analytical expression given by eq. (3) in the middle panels of Figures 2 and 3, therefore, acts as a smoothing procedure, eliminating the artifacts of applying the harmonic approximation (which we had to apply because of the prohibitively high computational cost and huge estimated amount of wall-clock time to compute the respective PMF's by Monte Carlo simulations of terminally-blocked amino-acid residues with the AM1 Hamiltonian).
The fitted Urot surfaces are generally in good qualitative agreement with the corresponding statistical potentials. However, for alanine (Figure 2a and Figure 3a), it can be observed that the low-PMF regions in the statistical potentials are narrower than in the corresponding fitted PMF's. The narrowing of Urot basins is even more apparent, if we compare the Urot surfaces determined by direct Monte Carlo simulations shown in Figure 4 of the accompanying paper1 and the statistical potentials. The only basin remaining in the statistical rotameric potential of the Ala residue corresponds to large values of α′, while the large basin present in the AM1-derived potential for θ = 90°, which is centered at about α′ = 105°, disappears. The basin around α′ = 105° corresponds to the neighborhood of the conformation, which has an energy only 1.67 kcal/mol above the global minimum ( in the AM1 energy surface of terminally-blocked Ala) but is virtually inaccessible for L-Ala residues in proteins because of interactions with neighboring residues with larger side chains.
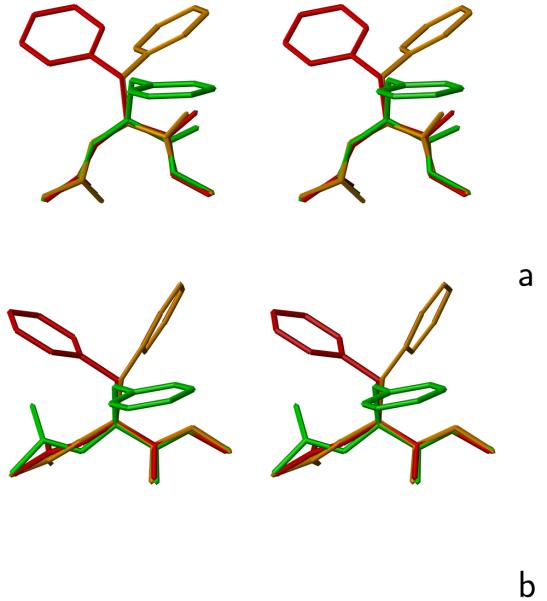
Fig. 4.
Representative rotamers of the Phe side chain for (a) θ ≈ 90° and (b) θ ≈ 140°. The rotamers of the side chain referred to in the text are color coded: red – rotamer 1, orange – rotamer 2, green – rotamer 3. The drawings were done with MOLMOL.29 The colors of the rotamers have been chosen to match their free energies, as shown in Figures 2d and 3d, middle panels.
In contrast to alanine, the surface of the statistical rotamer potential of proline (Figure 2 b, right panel) contains a broader basin than that of the AM1-derived potential (Figure 2 b, left panel). The angle α′ spreads from 70° to 130° while it stays around 120° for the AM1-derived potential. This difference can be attributed to greater distortion of the pyrollidine ring in the context of long-range interactions than in an isolated terminally-blocked proline residue.
For phenylalanine (Figure 2d and 3d), as well as for other residues with two χ angles (Figures S1 and S2 of Supplementary Material), the statistical potentials have more pronounced and more divided rotamer basins. The statistical potentials of these residues exhibit three major basins of rotamers at around (α′ = 150°, β′ = −150°), (α′ = 150°, β′ = 15°), and (α′ = 100°, β′ = −70°), respectively. The appearance of these three basins reflects the threefold potential of rotation about the Cα−Cβ bond (the χ1 angle). On the other hand, the basins are more differentiated by the free energy for the AM1-derived potentials compared to the statistical potentials. For θ = 90°, the first basin is the largest and has the lowest free energy. A plausible explanation of this observation is that the λ(1) and λ(2) (as well as the Φ and ψ) angles are smaller than 90° in absolute value for θ ≈ 90° (see, e.g., Figure 5 in ref. 16 and, because of the L-chirality of the natural amino acids, λ1 is negative. Therefore, for the first rotamer, the atoms of the backbone closest to those of the side chain are the amide nitrogen and amide hydrogen located between the and atoms, which form a group small in size and, therefore, not conflicting with side-chain atoms, as illustrated in Figure 4a as a sample conformation marked in red.
Fig. 5.
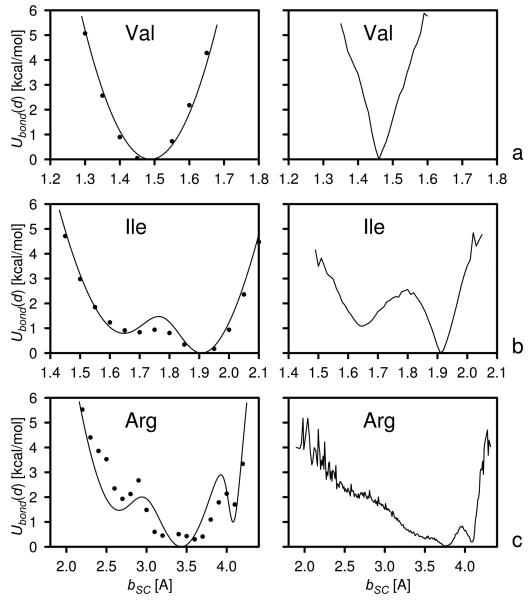
The Ubond curves of the side chains of selected amino-acid residues: Val (a), Ile (b), and Arg (c). Left panels: the potentials of mean force calculated from non-adiabatic AM1 energy surfaces with the use of the harmonic-approximation procedure described in the accompanying paper1 (filled circles) and by fitting eq. (8) to these surfaces (solid lines). Right panels: the corresponding statistical potentials (solid lines).
In the second rotamer (Figure 4a, orange drawing), the side-chain atoms are close to the carbonyl oxygen atom of the peptide group located between and which results in closer contacts between the backbone and side-chain atoms and, therefore, in both a narrower basin of this rotamer and a higher free energy compared to that of the basin of the first rotamer. In the statistical potential, the energy of the second rotamer is not increased much at the minimum, while it is increased by more than 2 kcal/mol in the AM1-derived potentials (Figure 2d); this observation can be explained by the influence of long-range interactions which are implicitly present in the statistical potentials. In the third rotamer, the side-chain atoms point towards the backbone (Figure 4a, green drawing) and are, therefore, close to the backbone atoms, which is manifested as more pronounced reduction of the size of the basin of the corresponding minimum and energy increase of the basin corresponding to this rotamer; again it is more pronounced in the AM1-derived potentials (Figure 2d).
For θ = 140°, the basins of all Phe rotamers have almost the same size and free energy in the statistical potential (Figure 3d). However, in the AM1-derived potentials, the second rotamer has the lowest free energy and the third rotamer is next in free energy. This is because the angles λ(1) and λ(2) are greater than 90° in absolute value and, therefore, the carbonyl group of the peptide unit located between and is closest to the side-chain atoms in the first rotamer (Figure 4b, red drawing), while the (smaller) amide group of the peptide unit located between and is the closest in the second rotamer. The lack of a remarkable free-energy difference between the three rotamers in the statistical potential, as opposed to the AM1-derived potential can be explained by the influence of interactions farther than within a single terminally-blocked residue; these interactions are manifested in the statistical potentials but not in the AM1-derived potentials.
The rotamer structure of the Urot free-energy surfaces of glutamic acid (Figure 2e and 3e) and other residues with three significant χ angles (Figures S1 and S2 of Supplementary Material) is much more diffuse because of greater flexibility of the side chains. However, the dominance of the first rotamer for θ = 90° and of the second rotamer observed for phenylalanine for θ = 140° is still observed for Glu (Figure 2e and 3e). For residues with four variable dihedral angles, arginine (Figure 2f and 3f) and lysine (Figures S2 and S2 of Supplementary Material) there is effectively one large basin with low free energy.
3.2 Virtual-bond-deformation potentials
Representative virtual-bond-deformation potential (Ubond) curves, obtained from the AM1 energy surfaces together with fitted curves described by eq. (8), and the corresponding statistical potentials for valine, isoleucine, and arginine, are shown in Figure 5. The force constant of the harmonic potential for deformation of the virtual Cα ⋯ Cα bonds bordering the peptide groups was calculated from eq. (33) of the accompanying paper,1 using the Hessian matrix calculated in this work with the quantum-mechanical ab initio method with the 6-31G** basis set for energy-minimized trans-N-acetyl-N′-methylacetamide. The equilibrium length of 3.8 Å of this virtual bond was kept from our previous work.6 The Ubond curves for all 19 natural amino-acid residues are shown in Figure S3 of the Supplementary Material. For illustration, we chose the residues representing unimodal (Val), bimodal (Ile), and more than bimodal (Arg) potentials. The coefficients of eq. (8) for all 19 natural amino-acid residues with side chains and of the trans peptide bond are summarized in Table 2. When fitting, we assumed no more than three terms in eq. (8), which corresponded to the number of dominant basins of minima in Ubond even for most structured curves; we assumed that the substructure could very well be an artifact of applying our harmonic-approximation-based procedure (see the accompanying paper) to compute the respective PMF's. Moreover, too rugged Ubond potentials could cause problems in integrating the equations of motion because of high forces coming from these potentials between the minima. It can be seen from the left panels of Figure 5 that, in spite of using a minimal number of terms, the fit is quite good even for the most structured PMF surface of arginine; the greater free-energy differences arise only in the higher-energy regions.
Table 2.
Parameters of eq. (8) obtained by fitting this equation to the AM1-derived PMF surfaces corresponding to Ubond.
| Residue | na | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [Å] | [kcal/mol × Å2] |
[kcal/mol] | [Å] | [kcal/mol × Å2] |
[kcal/mol] | [Å] | [kcal/mol × Å2] |
[kcal/mol] | ||
| pb | 1 | 3.800 | 41.7 | 0.000 | ||||||
| Cys | 1 | 1.396 | 243.1 | 0.000 | ||||||
| Met | 2 | 2.103 | 71.3 | 0.850 | 2.500 | 128.0 | 0.033 | |||
| Phe | 1 | 2.997 | 124.6 | 0.000 | ||||||
| Ile | 2 | 1.645 | 260.7 | 0.857 | 1.908 | 312.6 | .00010 | |||
| Leu | 2 | 1.782 | 638.3 | 2.360 | 2.086 | 160.4 | 0.409 | |||
| Val | 1 | 1.488 | 294.4 | 0.000 | ||||||
| Trp | 2 | 3.368 | 123.1 | 0.000 | 3.686 | 129.1 | .00049 | |||
| Tyr | 1 | 3.362 | 113.2 | 0.000 | ||||||
| Ala | 1 | 0.778 | 353.0 | 0.000 | ||||||
| Thr | 1 | 1.480 | 295.8 | 0.000 | ||||||
| Ser | 1 | 1.311 | 269.6 | 0.000 | ||||||
| Gln | 3 | 2.125 | 147.9 | 2.125 | 2.424 | 138.9 | .0333 | 2.776 | 383.8 | 0.000 |
| Asn | 1 | 2.008 | 161.4 | 0.000 | ||||||
| Glu | 3 | 2.093 | 131.2 | 1.943 | 2.425 | 146.5 | .0263 | 2.784 | 479.3 | 0.784 |
| Asp | 1 | 2.030 | 160.2 | 0.000 | ||||||
| His | 1 | 2.739 | 134.5 | 0.000 | ||||||
| Arg | 3 | 2.644 | 48.8 | 1.707 | 3.433 | 34.8 | .00123 | 4.080 | 899.9 | 1.175 |
| Lys | 3 | 2.379 | 99.0 | 1.974 | 2.704 | 157.5 | 0.546 | 3.073 | 164.7 | 0.055 |
| Pro | 1 | 1.422 | 605.2 | 0.000 |
Number of terms in eq. (8).
Trans peptide group.
It can be seen from Table 2 that the number of terms in eq. (8) is not directly related to the number of significant χ angles. The potentials are unimodal not only for Ala, Pro, Cys, Ser, Thr, and Val which have zero or one significant χ angle and where the distortion of the Cα ⋯ SC virtual bond length means distortion of the valence geometry but also for Asn, Asp, His, Phe, and Tyr which have two significant dihedral angles. The reason for this is that variation of the second dihedral angle (χ2) involves rotation of a rigid fragment about an axis which is equal to or close to its symmetry axis and, consequently, does not change the location of the side-chain center. The Ile, Leu, and Trp residues, for which the variation of χ2 changes the location of the side-chain center, exhibit clear bimodal Ubond potentials (see Figure 5b for an example). Residues with more than 2 significant χ angles have three major basins in the Ubond potentials (see Figure 5c for an example).
The regions of minima in the statistical potentials exhibit a V-like shape, which is most apparent for unimodal potentials (see the right panel of Figure 5 for an example). The V-like shape occurs even for alanine where the Cα ⋯ SC bond is half of the Cα−Cβ bond and the shape of its free-energy (effectively the potential-energy) curve could be expected to reflect the Morse potential curve near the equilibrium distance. The regions of minima in the statistical potentials are also much narrower compared to those derived from AM1 energy surfaces. The narrowing of the basins of minima certainly is the effect of applying restraints on bond lengths and bond angles and on some of the dihedral angles (or distances related to the bond and dihedral angles) in the refinement of X-ray or NMR structures.30, 31 The V-like shape of the statistical potentials should therefore be regarded as the effect of long-range interactions, which result in the distortion of bond lengths and bond angles. On the other hand, the number and positions of minima in the AM1-derived potentials correspond quite well to those in the statistical potentials.
The minima at the largest Cα ⋯ SC distances (corresponding to fully-extended side chains) in the bimodal and multimodal statistical Ubond potentials of the polar and charged residues (Glu, Gln, Arg, and Lys) have the lowest free energy. For the AM1-derived potentials of these residues, the free energy of the minima corresponding to more folded side-chain conformations is lower or only slightly higher than that of the extended conformations. The lower free energy of the minima corresponding to the extended side-chain conformations in the statistical potentials can readily be explained by better exposure of these side chains to the solvent when they are in extended conformations.
3.3 Optimization and tests of the force field
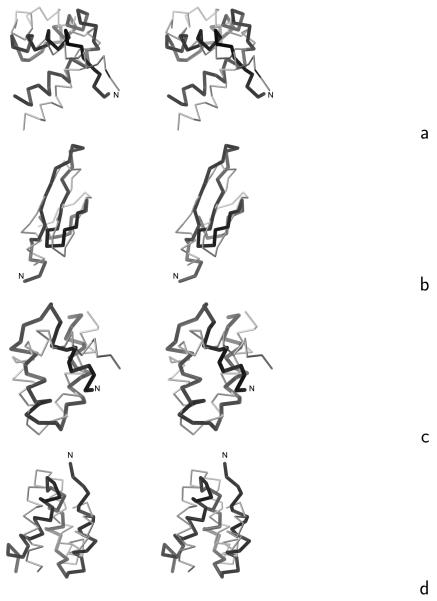
The initial and optimized energy-term weights (optimized using the 1ENH and 1E0L training proteins, as described in section 2.4) are summarized in Table 3, while the coefficients of the Fourier expansion of the energy surfaces of terminally-blocked amino-acid residues and the well-depths of the Gay-Berne potentials of side-chain interactions are summarized in Tables S3 and S4, respectively, of the Supplementary Material. We carried out 12 consecutive iterations of optimization obtaining a force field with folding-transition temperatures of Tf = 327 K for 1ENH, the experimental value24 being Tf = 325 K and Tf = 331 K for 1E0L, the experimental value23 being Tf = 339 K. The average structures of the dominant clusters of 1ENH and 1E0L below the folding-transition temperatures are shown in Figure 6a and b, respectively. Cluster analysis was carried out using the single-link method32, 33 and the average structures were determined and cluster probabilities calculated as described in our earlier work.14 The ensemble-averaged RMSD below the folding-transition temperature is about 6 Å for both proteins and the RMSD's from the averaged structures are 5.6 and 4.7 Å for 1ENH and 1E0L, respectively. Thus, the force field is a low-resolution force field for the training proteins. However, although further optimization using the procedure described in ref. 14, which is based on one starting set of energy-function parameters, resulted in gradually improved force-field resolution for the training proteins, this improvement was achieved at unacceptable expense of force-field transferability. We are now working on an improved optimization procedure, which is based on extensive search of energy-function-parameter space, and preliminary results are promising.34 Therefore, because the main purpose of this work was the design and parameterization of physics-based side-chain-rotamer and virtual-bond-deformation potentials, we leave detailed force-field optimization to our future work.
Table 3.
Initial and optimized energy-term weights (eq. 1 of the accompanynig paper4)
| weighta | initial | final |
|---|---|---|
| wSC | 1.11988 | 1.19736 |
| wSCp | 1.52281 | 1.99420 |
| 0.74945 | 1.42017 | |
| 0.11371 | 0.20992 | |
| wb | 1.10857 | 0.99918 |
| wrot | 0.16147 | 0.26686 |
| wtor | 1.95687 | 2.91850 |
| wtord | 1.62540 | 1.31981 |
| 0.24313 | 0.13636 | |
| 0.34502 | 0.04075 | |
| 1.74649 | 2.87486 | |
| 0.61716 | 1.76570 |
Fig. 6.
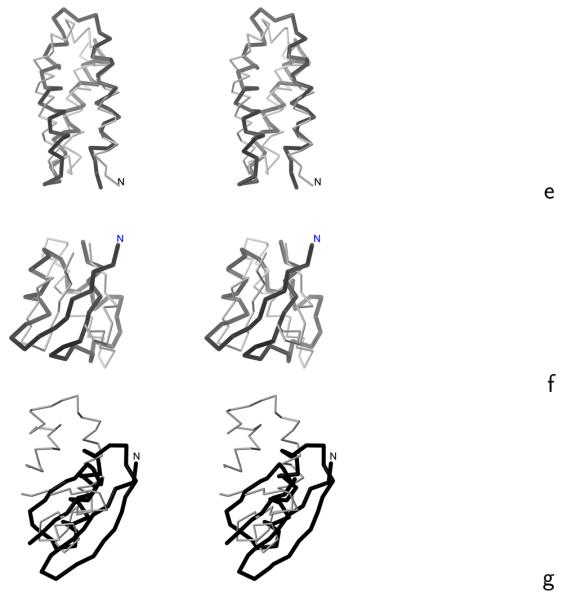
Stereoscopic views of the Cα traces of the average structures of the most native-like clusters of the proteins studied obtained in MREMD simulations with the UNRES force field incorporating the physics-based Ub potentials introduced in ref. 4 and the physics-based Urot and Ubond potentials introduced in this work (grey thin sticks) superposed on the Cα traces of the corresponding experimental structures (black thick sticks): (a) 1ENH, (b) 1E0L, (c) 1BDD, (d) 1GAB, (e) 1LQ7, (f) 1E0G, (g) 1PGA. For 1PGA only the fragments encompassing the middle helix and C-terminal β-hairpin (from residues 20 to 56) are superposed. The RMSD's between the computed and the experimental structures are listed in the ρave column of Table 4. The drawings were done with MOLMOL.29
We tested the transferability of the force field with 9 proteins of various structural classes: 1BDD, 1GAB, 1LQ7, 1KOY, 1CLB (α), 1E0G, 1PGA (α + β), 1I6C, and 1BK2 (β). Low-resolution native-like structures forming the most probable or the second most probable cluster were obtained for 1BDD, 1GAB, 1LQ7, and 1E0G. The average structures of these proteins obtained in simulations, superposed on the respective experimental structures, are shown in Figure 6c – f, while the ranks of native clusters, RMSD values, and the probabilities of the most native-like clusters are summarized in Table 4. For 1PGA, the native structure of which is composed of two β-hairpins forming a four-stranded β-sheet and a middle α-helix packed to it, the second cluster contains the middle helix and the C-terminal β-hairpin, while the N-terminal β-hairpin remains unfolded (Figure 6g). The simulated structures of the remaining proteins of the test set: 1KOY, 1CLB, 1I6C, and 1BK2 exhibited wrong secondary structure. Nevertheless, this first attempt at optimizing UNRES, with the old knowledge-based Ub, Urot, and Ubond terms, replaced with physics-based terms, has resulted in a force field of predictive power comparable to those derived by us earlier with knowledge-based local potentials.13, 14 Therefore, implicit consideration of protein context in the knowledge-based local potentials, which could be expected to result in better geometry and orientation of side chains, does not seem to be important.
Table 4.
Results of MREMD simulations of the training proteins 1ENH and 1E0L and the five test proteins for which native-like or partially native-like structures were obtained
| Protein | length | type | ρ cuta | Tclustb | rankc | %natived | ρ ¯ e | ρ minf | ρ aveg |
|---|---|---|---|---|---|---|---|---|---|
| 1ENH | 54 | α | 3.0 | 300 | 1 | 99 | 5.7 | 3.1 | 5.6 |
| 1E0L | 37 | α | 3.0 | 305 | 1 | 84 | 5.6 | 3.5 | 4.7 |
| 1BDD | 46 | α | 2.0 | 280 | 1 | 80 | 5.7 | 2.2 | 4.7 |
| 1GAB | 47 | α | 3.0 | 300 | 1 | 78 | 6.6 | 3.6 | 6.5 |
| 1LQ7 | 67 | α | 4.0 | 280 | 1 | 53 | 4.7 | 3.3 | 3.6 |
| 1E0G | 48 | α + β | 4.0 | 320 | 2 | 22 | 6.3 | 4.4 | 5.4 |
| 1PGA | 56 | α + β | 3.0 | 300 | 2 | 25 | 11.8 | 6.9 | 5.6h |
The RMSD cut-off in single-link clustering.
Temperature at which the probabilities of the clusters were calculated (always below the folding-transition temperature obtained from simulations as the position of the heat-capacity peak).
Rank of the native-like cluster (according to decreasing probability).
% occupancy of the native-like cluster at Tclust.
Ensemble-averaged RMSD (Å) over the conformations of the native-like cluster at Tclust.
Minimum RMSD (Å) obtained during the whole MREMD simulation.
RMSD (Å) of the average conformation of the native-like cluster.
Residues 20-56 were superposed to compute ρave.
3.4 Effect of introducing the new Urot potentials on the stability of mesoscopic dynamics with UNRES
In the implementation of earlier versions of UNRES, which contained old knowledge-based Urot potentials, the stability of the MD integration algorithm was a problem.5 The reason for this was that the old Urot potentials were expressed as logarithms of sums of Gaussians in the angles α′ and β′, which resulted in discontinuity of the forces and, thereby, instability of the integration algorithm.5 We minimized this problem by introducing a variable-time-step (VTS) algorithm5 and, subsequently, modifying the reversible reference system propagator (RESPA) version35 of the multiple-time-step (MTS) algorithm36 to obtain the adaptive multiple time step (A-MTS) algorithm.37 However, we noted that changing only the functional form of Urot to one with a stable Cartesian gradient will provide a real solution of the problem. The functional form introduced in this work and expressed by eq. (3) does not contain explicit polar angles α′ and β′ and, consequently, does not generate unstable gradients of Urot.
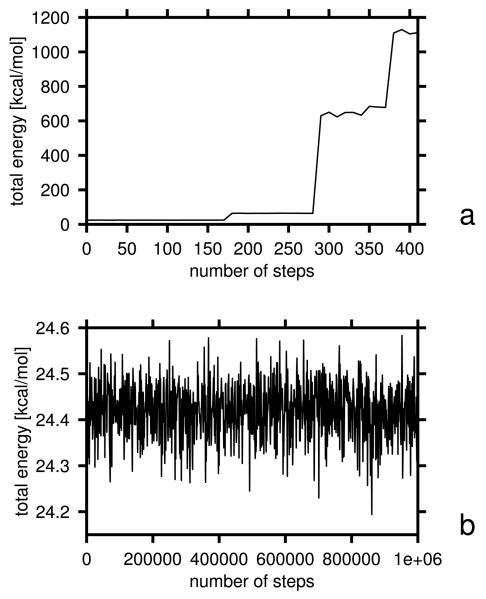
To compare the stability of the algorithm with old and new Urot, we ran 1,000,000 microcanonical MD steps on decaalanine, starting from an α-helical conformation, as in the test of energy conservation performed in our earlier work.37,38 The integration-time step was 4.89 fs (0.1 mtu; molecular time units5), which gives a total of 4.89 ns trajectory length. For the run with the old knowledge-based Urot, we used the force field optimized in our earlier work14 on 1GAB, while, for that with the new potentials, we used the force field optimized in this work (section 3.3). The total energy of the system is plotted as a function of the number of steps for the run with the old and new Urot potentials in Figure 7a and b, respectively. As can be seen from Figure 7a, the energy rises by over 1,000 kcal/mol after 400 MD steps for the old potentials, while it only oscillates about a value close to the initial value for the new potentials (Figure 7b). Thus, introduction of the Urot potentials of eq. (3) eliminated gradient instability, as expected. It should be noted, however, that this improvement was achieved by changing the functional form of Urot rather than by a physics-based origin of the new potentials. The Urot of eq. (3), fitted to statistical potentials, would also generate a stable gradient.
Fig. 7.
Plots of total energy vs. number of MD steps in microcanonical simulations of decaalanine with the time step δt = 4.89 fs in a run with (a) old Urot, Ubond, and Ub potentials and (b) and with the new potentials.
4 Conclusions
In this work, we determined and implemented in the UNRES force field new physics-based side-chain rotamer (Urot) and virtual-bond-distortion (Ubond) potentials, which replaced the knowledge-based potentials5, 7 used in the earlier MD implementations of UNRES.5, 14, 38, 39 We demonstrated (section 3.3) that, after initial optimization, the force field with the new Urot and Ubond potentials as well as with the new virtual-bond-angle-bending (Ub) potentials introduced in our earlier work,4 is reasonably transferable producing low-resolution stable native-like structures which form the most probable or second most probable clusters of conformations in unrestricted MD simulations of 4 out of 9 proteins outside the training set; for one more protein of α + β structural type (1PGA) the conformations of the second probable cluster capture part of the native structure. We are currently working on large-scale optimization of the force field based on extensive search of parameter space.34 Replacement of the old formulas for Urot, which contained explicit polar angles,7 with new ones [eq. (3)] expressed in the local Cartesian coordinates of the Cα ⋯ SC virtual-bond vectors, eliminated the persistent problem of the instability of the gradient of Urot in MD simulations observed in earlier version of UNRES MD which implemented the old Urot potentials.5
The Urot potentials determined from AM1 energy surfaces and the statistical potentials share many features, namely, location of the low-free-energy regions on the “southern hemisphere” of the (α′, β′) angle space, large bias towards negative β′ angles, reduction of the low-free-energy region with increasing angle θ, increasing spread of the low-free-energy region with the number of significant side-chain χ angles, and the appearance of three distinct major basins of minima corresponding to rotamers about the Cα−Cβ axis for residues with two significant χ angles. These general features result from the chemical structure and L-chirality of natural amino acids and are, therefore, independent of whether a residue is isolated or placed within a protein. However, the effect of protein context results in remarkable differences between the AM1-derived and statistical potentials. For alanine and other residues with small side chains, there is a well-defined minimum for α′ close to 105° in the Urot surface calculated at θ = 90°, which contains contributions from the region of the conformation, while this minimum does not appear in the statistical potentials (Figure 2a). The conformation has energy only 1.67 kcal/mol above the global minimum; it is also relatively low in energy in the ab initio energy surfaces of terminally-blocked L-alanine.11 For valine, which has a larger side chain, this minimum does not appear in the AM1-derived and statistical potentials.
As we demonstrated in the accompanying paper,1 including solvation at the mean-field level does not eliminate the minimum at α′, close to 105°. Moreover, backbone peptide groups are largely dehydrated in folded proteins.40 We can, therefore, conclude that residues surrounding alanine force this residue to avoid the conformation by forcing its peptide groups to assume the angles of rotation resulting in low local-interaction energy of the neighboring larger residues. Long-range interactions between the peptide groups of alanine and those of residues farther in sequence might also contribute here, because they influence the angles of rotation of the peptide group. However, because we derived the statistical potentials from the parts of PDB structures not involved in regular secondary structures, which minimizes the number of backbone hydrogen bonds between remote residues, the interactions within the nearest neighbors are, probably, the main source of context contribution to the statistical Urot potentials. The nearest-neighbor and long-range backbone hydrogen-bond interactions probably also account for much less pronounced differences in the free energy of different rotamers of side chains with two significant χ angles compared to AM1-derived Urot potentials, in which the rotamers are significantly differentiated by free energy (Figure 2c and 3c). This suggests that, in order to reproduce side-chain orientations correctly, it will be necessary to introduce cooperative terms between the rotamer states and backbone-local interactions. Possible candidates for such correlation contributions are the additional torsional potentials involving Cα ⋯ SC virtual bonds such as, e.g., potentials composed of terms accounting for the energetics of rotation about the Cα ⋯Cα ⋯Cα ⋯ SC, SC⋯Cα ⋯Cα ⋯Cα, and SC⋯Cα ⋯Cα ⋯SC virtual-bond axes. Work on these potentials is currently underway in our laboratory.
The Ubond potentials introduced in this work are qualitatively different from their harmonic-only predecessors introduced in the first version of UNRES MD.5 For larger side chains, the Ubond surface is definitely multimodal, which is reflected in the new potentials. The number and positions of minima in the AM1-derived potentials correspond to those in statistical potentials. However, the regions of minima in the statistical potentials are much narrower than the AM1-derived potentials and are V-shaped and not parabolic-shaped or Morse-curve-shaped, which is most likely the effect of applying restraints on bond lengths and bond angles in X-ray or NMR-structure refinement. To fit the region of a minimum in statistical Ubond even for simple residues such as alanine or valine, a force constant exceeding 1000 kcal/(mol×Å2) is required, which is clearly unphysical. Consequently, protein structural data do not appear to be a good source of data to derive virtual-bond-deformation potentials. Artifacts from restraints certainly influence other local statistical potentials (such as the Urot and Ub in UNRES) and it is, therefore, not clear how significant is the influence of restraints in structure refinement on the results of simulations with statistical potentials derived from protein structural data. Physics-based potentials which are free from such artifacts appear more reliable in this regard.
Finally, the harmonic approximation introduced in our earlier work4 and developed further in the accompanying paper1 appears to be a relatively fast and inexpensive tool to derive local coarse-grained potentials, and enables us to compute the respective energy surfaces at the quantum-mechanical level. If the PMF's were derived from Monte Carlo or molecular dynamics simulations, the use of molecular quantum mechanics would be impractical and the all-atom energy would have to be calculated with an all-atom force field, which is far less accurate. The harmonic-approximation method enables us to scan the entire energy surface of a system under study using a relatively small number of significant variables and treat the contributions of the other, rigid, variables in an approximate manner. It can, therefore, be applied generally to derive the local-interaction potentials for coarse-grained systems.
Supplementary Material
Acknowledgments
This work was supported by grants from the Polish Ministry of Science and Higher Education (0490/B/H03/2008/35), the National Institute of Health (GM-14312), and the National Science Foundation (MCB05-41633). This research was conducted by using the resources of (a) our 800-processor Beowulf cluster at Baker Laboratory of Chemistry, Cornell University, (b) the National Science Foundation Terascale Computing System at the Pittsburgh Supercomputer Center, (c) the John von Neumann Institute for Computing at the Central Institute for Applied Mathematics, Forschungszentrum Jülich, Germany, (d) our 45-processor Beowulf cluster at the Faculty of Chemistry, University of Gdańsk, (e) the Informatics Center of the Metropolitan Academic Network (IC MAN) in Gdańsk, and (f) the Interdisciplinary Center of Mathematical and Computer Modeling (ICM) at the University of Warsaw.
References
- 1.Kozłowska U, Liwo A, Scheraga HA. J. Comput. Chem. 2009 doi: 10.1002/jcc.21399. accompanying paper. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Stewart JJ. J. Comput.-Aided Molec. Design. 1990;4:1. doi: 10.1007/BF00128336. [DOI] [PubMed] [Google Scholar]
- 3.Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. Nucl. Acid Res. 2000;28:235. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kozłowska U, Liwo A, Scheraga HA. J. Phys.: Cond. Matter. 2007;19:285203. [Google Scholar]
- 5.Khalili M, Liwo A, Rakowski F, Grochowski P, Scheraga HA. J. Phys. Chem. B. 2005;109:13785. doi: 10.1021/jp058008o. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Liwo A, Ołdziej S, Pincus MR, Wawak RJ, Rackovsky S, Scheraga HA. J. Comput. Chem. 1997;18:849. [Google Scholar]
- 7.Liwo A, Pincus MR, Wawak RJ, Rackovsky S, Ołdziej S, Scheraga HA. J. Comput. Chem. 1997;18:874. [Google Scholar]
- 8.Liwo A, Kaźmierkiewicz R, Czaplewski C, Groth M, Ołdziej S, Wawak RJ, Rackovsky S, Pincus MR, Scheraga HA. J. Comput. Chem. 1998;19:259. [Google Scholar]
- 9.Liwo A, Czaplewski C, Pillardy J, Scheraga HA. J. Chem. Phys. 2001;115:2323. [Google Scholar]
- 10.Liwo A, Arłukowicz P, Czaplewski C, Ołdziej S, Pillardy J, Scheraga HA. Proc. Natl. Acad. Sci. U.S.A. 2002;99:1937. doi: 10.1073/pnas.032675399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ołdziej S, Kozłowska U, Liwo A, Scheraga HA. J. Phys. Chem. A. 2003;107:8035. [Google Scholar]
- 12.Liwo A, Ołdziej S, Czaplewski C, Kozłowska U, Scheraga HA. J. Phys. Chem. B. 2004;108:9421. [Google Scholar]
- 13.Ołdziej S, Ła̧giewka J, Liwo A, Czaplewski C, Chinchio M, Nanias M, Scheraga HA. J. Phys. Chem. B. 2004;108:16950. [Google Scholar]
- 14.Liwo A, Khalili M, Czaplewski C, Kalinowski S, Ołdziej S, Wachucik K, Scheraga HA. J. Phys. Chem. B. 2007;111:260. doi: 10.1021/jp065380a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Liwo A, Czaplewski C, Ołdziej S, Rojas AV, Kaźmierkiewicz R, Makowski M, Murarka RK, Scheraga HA. Simulation of protein structure and dynamics with the coarse-grained UNRES force field. In: Voth G, editor. Coarse-Graining of Condensed Phase and Biomolecular Systems. 2008. chapter 8, 1391, 2008. [Google Scholar]
- 16.Nishikawa K, Momany FA, Scheraga HA. Macromolecules. 1974;7:797. doi: 10.1021/ma60042a020. [DOI] [PubMed] [Google Scholar]
- 17.Rodríguez AM, Baldoni HA, Suvire F, Vázquez RN, Zamarbide G, Enriz RD, Farkas Ö, Perczel A, McAllister MA, Torday LL, Papp JG, Csizmadia IG. J. Mol. Struct. THEOCHEM. 1998;455:275. [Google Scholar]
- 18.MOPAC . Fujitsu Inc; 2003. [Google Scholar]
- 19.Marquardt DW. J. Soc. Indust. Appl. Math. 1963;11:431. [Google Scholar]
- 20.Ołdziej S, Liwo A, Czaplewski C, Pillardy J, Scheraga HA. J. Phys. Chem. B. 2004;108:16934. [Google Scholar]
- 21.Clarke ND, Kissinger CR, Desjarlais J, illiland GLG, Pabo CO. Protein Sci. 1994;3:1779. doi: 10.1002/pro.5560031018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Macias MJ, Gervais V, Civera C, Oschkinat H. Nat. Struct. Biol. 2000;7:375. doi: 10.1038/75144. [DOI] [PubMed] [Google Scholar]
- 23.Nguyen H, Jäger M, Moretto A, Gruebele M, Kelly JW. Proc. Natl. Acad. Sci. U.S.A. 2003;100:3948. doi: 10.1073/pnas.0538054100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mayor U, Grossman JG, Foster NW, Freund SMV, Fersht AR. J. Mol. Biol. 2003;333:977. doi: 10.1016/j.jmb.2003.08.062. [DOI] [PubMed] [Google Scholar]
- 25.Rhee YM, Pande VS. Biophys. J. 2003;84:775. doi: 10.1016/S0006-3495(03)74897-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nanias M, Czaplewski C, Scheraga HA. J. Chem. Theor. Comput. 2006;2:513. doi: 10.1021/ct050253o. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Czaplewski C, Kalinowski S, Liwo A, Scheraga HA. J. Chem. Theor. Comput. 2009;5:627. doi: 10.1021/ct800397z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kumar S, Bouzida D, Swendsen RH, Kollman PA, Rosenberg JM. J. Comput. Chem. 1992;13:1011. [Google Scholar]
- 29.Koradi R, Billeter M, Wüthrich K. J. Mol. Graphics. 1996;14:51. doi: 10.1016/0263-7855(96)00009-4. [DOI] [PubMed] [Google Scholar]
- 30.Hendrickson WA. Meth. Enzym. 1980;115:225. [Google Scholar]
- 31.Pearlman DA, Case DA, Caldwell JW, Ross WS, Cheatham TE, III, DeBolt S, Ferguson D, Seibel G, Kollman P. Comp. Phys. Commun. 1995;91:1. [Google Scholar]
- 32.Murtagh F. Multidimensional clustering algorithms. Physica-Verlag; Vienna: 1985. [Google Scholar]
- 33.Murtagh F, Heck A. Multivariate data analysis. Kluwer Academic Publishers; 1987. [Google Scholar]
- 34.He Y, Xiao Y, Liwo A, Scheraga HA. J. Comput. Chem. 2009 doi: 10.1002/jcc.21215. in press (Early View) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Tuckerman M, Berne BJ, Martyna GJ. J. Chem. Phys. 1992;97:1990. [Google Scholar]
- 36.Ciccotti G, Kalibaeva G. Phil. Trans. R. Soc. Lond. A. 2004;362:1583. doi: 10.1098/rsta.2004.1400. [DOI] [PubMed] [Google Scholar]
- 37.Rakowski F, Grochowski P, Lesyng B, Liwo A, Scheraga HA. J. Chem. Phys. 2006;125:204107. doi: 10.1063/1.2399526. [DOI] [PubMed] [Google Scholar]
- 38.Khalili M, Liwo A, Jagielska A, Scheraga HA. J. Phys. Chem. B. 2005;109:13798. doi: 10.1021/jp058007w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Liwo A, Khalili M, Scheraga HA. Proc. Natl. Acad. Sci. U.S.A. 2005;102:2362. doi: 10.1073/pnas.0408885102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Fernandez A, Kardos J, Goto Y. FEBS letters. 2003;536:197. doi: 10.1016/s0014-5793(03)00056-5. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.