Mechanical Property Characterization of Bilayered Tablets using Nondestructive Air-Coupled Acoustics

Abstract

A noncontact/nondestructive air-coupled acoustic technique to be potentially used in mechanical property determination of bilayer tablets is presented. In the reported experiments, a bilayer tablet is vibrated via an acoustic field of an air-coupled transducer in a frequency range sufficiently high to excite several vibrational modes (harmonics) of the tablet. The tablet vibrational transient responses at a number of measurement points on the tablet are acquired by a laser vibrometer in a noncontact manner. An iterative computational procedure based on the finite element method is utilized to extract the Young’s modulus, the Poisson’s ratio, and the mass density values of each layer material of a bilayer tablet from a subset of the measured resonance frequencies. For verification purposes, a contact ultrasonic technique based on the time-of-flight data of the longitudinal (pressure) and transverse (shear) acoustic waves in each layer of a bilayer tablet is also utilized. The extracted mechanical properties from the air-coupled acoustic data agree well with those determined from the contact ultrasonic measurements. The mechanical properties of solid oral dosage forms have been shown to impact its mechanical integrity, disintegration profile and the release rate of the drug in the digestive tract, thus potentially affecting its therapeutic response. The presented nondestructive technique provides greater insight into the mechanical properties of the bilayer tablets and has the potential to identify quality and performance problems related to the mechanical properties of the bilayer tablets early on the production process and, consequently, reduce associated cost and material waste.

INTRODUCTION

Today, the single most effective and repeatable solid oral dosage form for administering precise quantities of drug into the human blood stream accurately and reproducibly is the tablet. Solid oral dosage forms are the preferred route for many drugs and are still the most widely used formulations for new and existing complex-configuration dosage forms such as controlled-release (CR) (1–5), osmotic pumps (6), and dry-coated tablets (i.e., tablet within a tablet) (7,8). CR tablets are solid oral dosage forms from which the active drug is released over an extended period of time with the aim of decreasing the dosing frequency and reducing peak plasma concentrations. Because of the reduced fluctuation of the active drug in the blood stream, CR tablets are often deemed safer and more tolerable than conventional solid dosage forms, and have shown better patient compliance (9). With the advent of CR technology, due to the use of different materials and their complex geometric boundaries, the mechanical structures of these drug delivery systems have become quite intricate, requiring complicated tablet architectures as well as patient-friendly administration. Consequently, the CR drug delivery systems typically require more demanding mechanical testing, characterization, and monitoring techniques with faster response times than those possible with traditional measurement approaches (10–13).

In the past decade or so, it is observed that the interest in multilayered tablets as an oral CR system has substantially increased (1–5). Multilayered tablets have some key advantages compared to conventional (immediate-release) monolayer tablets. For instance, such tablets are commonly used to avoid chemical incompatibilities of formulation components by physical separation, and release profiles may be modified by combining layers with various release patterns, or by combining slow-release with immediate-release layers (7). Despite its various functional advantages, a number of issues associated with the mechanics and manufacturing of multilayered tablets have been reported in the recent years. Some of the major complications of multilayered tablets include insufficient hardness (4), inaccurate individual mass control (9), cross contamination between the layers (4–7), reduced yield, and their tendency to delaminate at the non-planer interface between the adjacent compacted layers (i.e., layer-separation) (4) during the various stages of production downstream of the compaction process. For instance, in 2005, the U.S. Food and Drug Administration (FDA) initiated seizures of some lots of Paxil CR® (Glaxo-Smith-Kline PLC, Brentford, England) CR bilayer tablets that were inadequately manufactured and announced that these tablets “could split apart and patients could receive a portion of the tablets that lacks any active ingredient, or alternatively a portion that contains active ingredient and does not have the intended controlled-release effect” (14). In this particular case, the residual stress distribution in the tablet is suspected to be a major cause of the loading of the particles and the resultant tablet inhomogeneity cause the tablet fracture and split apart (15). The fracture of multilayered tablets is often the result of an interfacial crack driven by residual stresses in the tablet propagating a finite distance within the tablet and leads to capping and lamination which may not always be immediately apparent immediately after compaction (4,15,16). It is known that occurrence of the fracture/crack at the interface causes a reduction in the overall elastic stiffness (Young’s modulus) and layered tablets become fragile and develop a tendency to fail. Therefore, while the therapeutic (chemical/pharmaceutical) functions of multilayered tablets are crucial, they need to have a certain degree of mechanical strength and ruggedness to survive normal processing, handling, packaging, and shipping stresses. Understanding what influences the stress state and mechanical properties of a multilayered tablet and develop specialized techniques for measuring those properties could then assist in the understanding of how, and why, defects such as capping, lamination, and cracking occur, which are significant practical problems for the pharmaceutical industry.

The FDA, with an interest in the improvement of manufacturing quality and development, has initiated a program entitled Process Analytical Technology (PAT) to address various aspects of manufacturing issues in the pharmaceutical industry and to forward the idea of improving the quality of the pharmaceutical products by a deeper understanding of the processes involved during manufacturing (17). The PAT framework encourages and advises the use of modern measurement and monitoring approaches such as the acoustic emission method (18,19), acoustic and ultrasonic characterization techniques (20–24), the near-infrared sensing (25), light-induced fluorescence characterization (26), Terahertz pulsed spectroscopy (27), laser-induced breakdown spectroscopy (28), X-ray fluorescence method (15), and Raman spectroscopy (29) for characterization and monitoring of tablets to ensure product quality by using on-, in-, and/or at-line measurements and through timely measurements (i.e., during processing) of critical quality and performance attributes of raw and in process materials and unit operations. The effectiveness of air-coupled acoustic technique, using an air-coupled excitation source and laser interferometric detection, has been demonstrated for the nondestructive characterization of the critical mechanical properties and coating thickness of enteric-coated monolayer tablets (21,22). In the current study, for the first time, the air-coupled acoustic technique is utilized for determining the Young’s modulus, the Poisson’s ratio, and the mass density values of the individual layer materials of a bilayer tablet. The bilayer test tablet is vibrated via an acoustic field generated by an air-coupled transducer in a frequency range sufficiently high to excite its several vibrational modes (harmonics). The transient vibrational responses of the bilayer tablet are acquired at a number of measurement points by a laser interferometer in a noncontact manner. An iterative computational procedure based on the finite element (FE) method, described below, is utilized to extract the mechanical properties of the bilayer tablet from a subset of its measured resonance frequencies. The mechanical properties extracted by this technique are compared to those obtained by a standard contact ultrasonic method based on time-of-flight (TOF) measurements and a good agreement is found.

MATERIALS AND METHODS

Materials

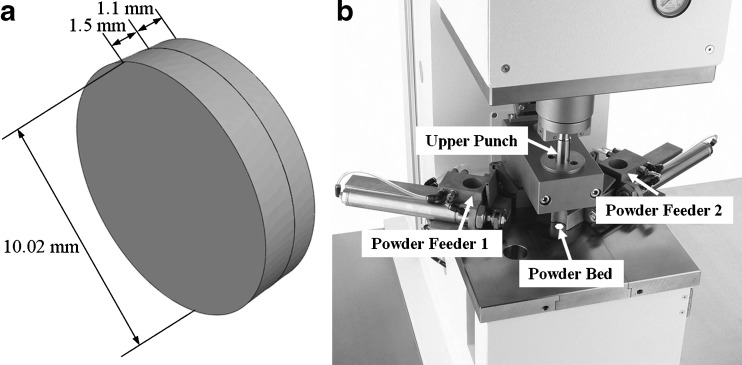
In the reported study, a set of bilayer test tablets (hereafter referred to as BL-tablets) with an average mass of 248 mg and with the characteristic dimensions of 10.02 ± 0.02 mm length and 2.6 ± 0.02 mm thickness are utilized. The tablet weight is measured using an electronic balance and the diameter and the layer thickness are measured with a digital caliper. From these measurements, the volume and packing density of the tablets are determined. The tablet geometry is depicted in Fig. 1. The powders selected for the layers of the BL-tablets include; (a) directly compressible lactose (DCL-14; Lot # L0751A4921, Meggle GmbH, Wasserburg, Germany) and (b) microcrystalline cellulose (MCC) in the form of Avicel PH102 (Lot # 310, FMC Corp., PA, USA). Particle size distributions, bulk densities, and true densities of the powders are tabulated in Table I. The mass median diameter of the powder particles are measured by a particle size analyzer (Malvern Mastersizer 2000, Malvern Instruments Ltd., Worcestershire, UK). True densities of the powders are determined by a helium pycnometer (AccuPyc II 1340, Micromeritics Corp., GA, USA). These powders are commonly used in CR tablet formulations (30).

Fig. 1.

a The configuration and dimensions of a sample bilayer tablet, b the automated single-station tablet press used for compaction of the BL-tablets

Table I.

Particle Size Distributions, Bulk Densities, and True Densities of the Powders Used

Powder	Particle size (μm)	Bulk density (kg/m3)	True density (kg/m3)
DCL-14	136.0 ± 2.5	530 ± 0.01	1,620 ± 0.01
MCC	113.8 ± 1.1	360 ± 0.01	1,520 ± 0.01

Methods

Compact Preparation

Bilayer tablets are compacted by uni-axial compression on a fully automated single-station tablet press (Flexitab®, OYSTAR Manesty Corp., Knowsley, UK; Fig. 1). In this tablet press as shown in Fig. 1, the bottom punch is stationary while the top punch is moving. A flat-faced punch with a diameter of 10 mm is used. There is no requirement for punch lubrication on this single punch tablet press. The first layer is formed by compressing the DCL-14 at 8 kN compression force. The second layer is then formed and bonded by compressing the MCC powder with the lactose tablet at 10 kN compression force. The compression dwell time is set to 100 ms to enable the formation of uniformly bonded compacts. Each powder layer is compressed to a target solid fraction of 0.75, when possible, which is a typical level for most pharmaceutical tablets (31).

Air-Coupled Acoustic Experimental Set-up and Configuration

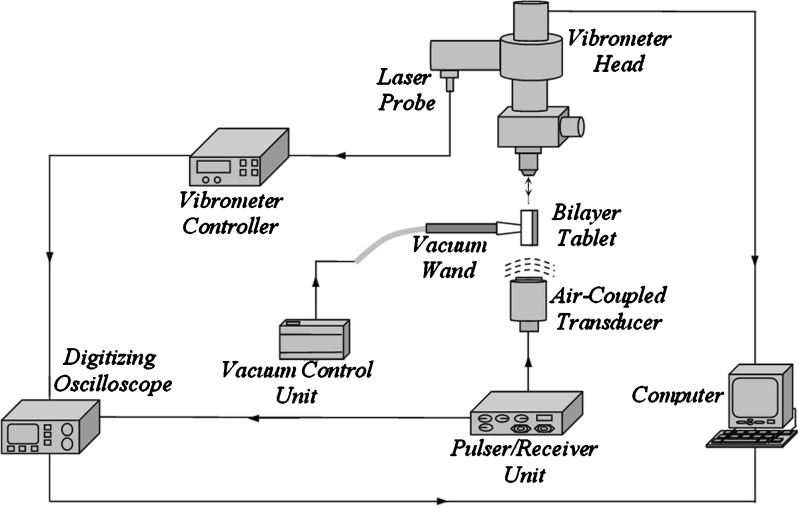
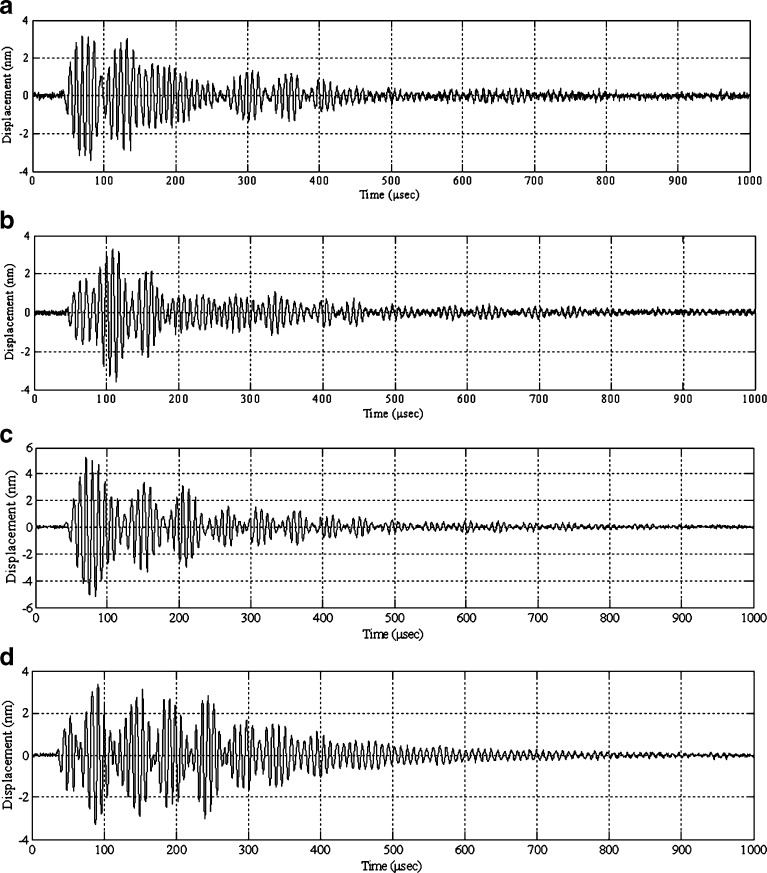
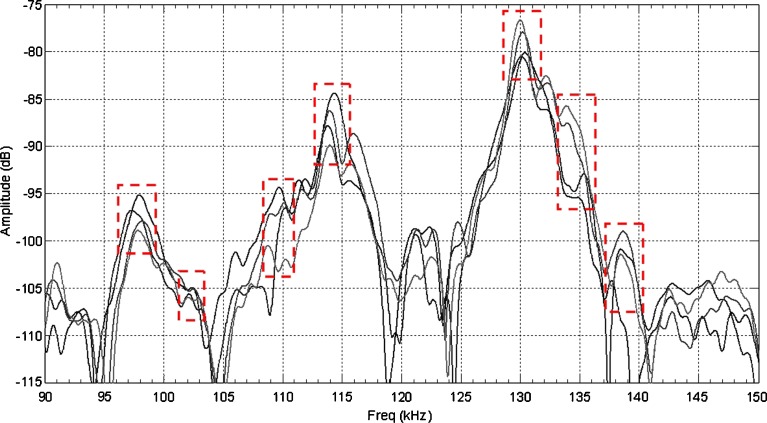
For demonstrating the utility and effectiveness of the air-coupled acoustic technique in mechanical property characterization and to determine the resonance frequencies based on air-coupled excitation and interferometric detection, a set of ten BL-tablets (the sample set) are employed and tested. The experimental set-up consists of a square pulser/receiver (Panametrics 5077PR), an air-coupled transducer (QMI AS120Ti), a laser interferometer (Polytec OFV511) integrated with an optical microscope, a vibrometer controller (Polytec OFV3001), a digitizing oscilloscope (Tektronix TDS3052), and a vacuum handling apparatus consisting of a vacuum wand and a vacuum pump with a suction power of −30 kPa (FVW-110 Duovac; Fig. 2). The air-coupled transducer with a frequency bandwidth of 95–150 kHz is excited by the pulser/receiver unit generating a square pulse at a central frequency of 120 kHz. This excitation leads to the out-of-plane vibrations of the active surface of the transducer and emits transient acoustic fields. The resulting acoustic field interacts with the BL-tablet and excites its several vibrational modes (harmonics) in the bandwidth of the air-coupled transducer. The laser interferometer, embedded into the optical microscope, has a frequency bandwidth of 20 kHz–30 MHz and includes a displacement decoder with sub-nanometer resolution in the range of ±75 nm. In the current air-coupled acoustic experiments, the transducer is placed vertically below the tablet, facing upward. The BL-tablet is brought above the transducer using the vacuum apparatus (Fig. 2). The tablet is placed near the focal distance of the transducer, which is specified as 2.35 mm. Preliminary tests with various tablet fixing mechanisms indicate that the boundary conditions due to mounting techniques of a tablet can play an important role in the accuracy and sensitivity of transient response measurements. An ideal tablet-holding configuration must only minimally interfere with the acoustic field exciting the vibrational motion of the tablet, while holding the tablet firmly in place with a minimal contact area. In other words, weak elastic coupling between the tablet and the fixing mechanism is required. In the reported study, a vacuum wand is utilized for holding the tablet. In order to observe the possible effect of the mechanical vibrations caused by the vacuum wand on the acquired tablet vibrational responses, the response of the vacuum wand to the air-coupled acoustic field is measured at several points on the wand. No vibration of the wand with significant amplitudes is observed. The pulser/receiver unit, which also provides a synchronizing pulse to trigger the digital oscilloscope, generates a pulsed acoustic field. The pulser/receiver unit used here delivers square pulses with amplitude of up to 400 V to the transmitting air-coupled transducer. In all the reported experiments, the pulser/receiver voltage is set to 400 V. The tablet transient responses (out-of-plane displacements) at a measurement point are acquired by the laser interferometer in a noncontact manner by detecting the phase shift of a reflected laser beam light. The laser interferometer embedded into the optical microscope is directly focused at points on the tablet surface through the objective lens of the microscope that is placed approximately 6.5 mm above the tablet surface. According to the specifications, the use of the microscope objective lens allows the laser probe beam to be focused at a spot that can be theoretically reduced to 0.5 μm using a ×100 microscope objective. The waveforms corresponding to the out-of-plane displacement of the tablet (Fig. 3) are acquired by the laser interferometer, digitized through the digital oscilloscope and uploaded to a computer for signal processing and spectral analysis to determine the vibrational resonance frequencies of the BL-tablet. The resonance frequencies of the sample set in the transducer bandwidth from the acquired digital waveforms are obtained by using the fast Fourier transform algorithm. Consistent waveforms obtained at various points of the sample set over an extended period of time indicated that the air-coupled acoustic excitation and the experimental set-up are repeatable. The responses of only four BL-tablets from the sample set are included here for clarity (Figs. 3 and 4). It is observed that the resonance frequencies of all the BL-tablets from the sample set are consistent. As detailed below, from a subset of the measured resonance frequencies of a BL-tablet in the specified bandwidth, its mechanical properties are extracted using a previously established iterative computational procedure (21,22).

Fig. 2.

The instrumentation diagram of the acoustic excitation and interferometric detection set-up for acquiring transient responses of tablets. Gray and white parts in the BL-tablet illustrate the MCC and the DCL-14 layers, respectively

Fig. 3.

Transient surface displacement responses of four BL-tablets under the noncontact air-coupled acoustic excitation with a 120-kHz transducer excited by a square pulse with a pulse width of 8.33 μs, and an amplitude of 400 V (a, b, c, d)

Fig. 4.

Resonance frequency spectra of four BL-tablets. Dashed rectangles mark the expected locations of the resonance frequencies of the BL-tablets

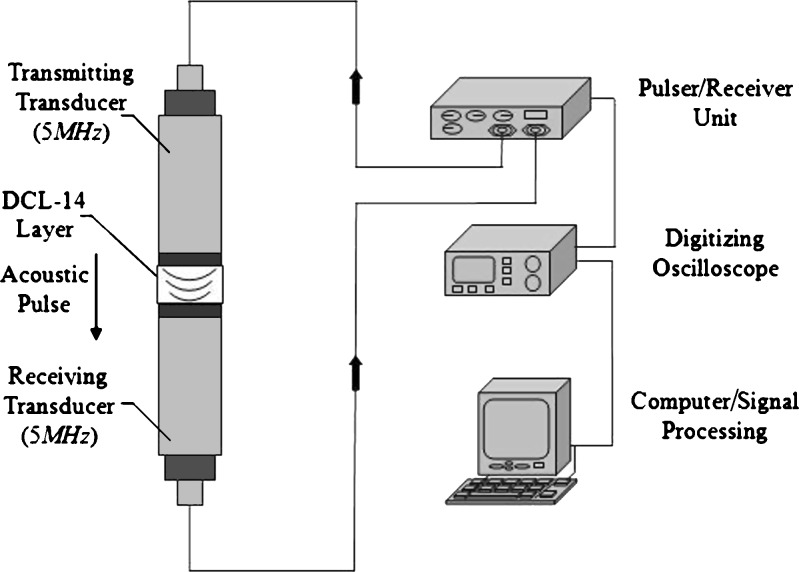
Contact Ultrasonic Measurements

To verify the results of the air-coupled acoustic method, a contact time-of-flight (TOF) ultrasonic study is conducted for the determination of the Young’s modulus and the Poisson’s ratio values of the DCL-14 and the MCC layers of the sample set. Various mechanical and elastic properties of a material (e.g., Young’s modulus E and Poisson’s ratio ν) can be extracted by measuring the acoustic properties of pressure and shear waves in the material. The experimental set-up developed for the ultrasonic evaluation consists of a pulser/receiver unit (Panametrics 5077PR), a pair of piezoelectric transducers with a central frequency of 5 MHz (F0730, Aerotech Inc.), a pair of piezoelectric shear wave transducers with a central frequency of 5 MHz (SF052, Valpey Fisher Inc.), a digitizing oscilloscope (Tektronix TDS3052), and a computer controlling the data acquisition (Fig. 5). In order to determine the Young’s modulus and the Poisson’s ratio values of each layer, sample set are carefully debonded from their interfaces. For the Young’s modulus extraction, the two piezoelectric transducers are placed in direct contact with the top and bottom surfaces of each flat-faced layer (DCL-14 and MCC). In order to minimize the damage to the layers tested, a thin, adhesive plastic tape layer with a thickness of d (d << λ, where λ denotes the ultrasonic wavelength) is used as an acoustic couplant instead of glycerin gel or shear gel. Acoustic impedance of the tablet material is much higher than the acoustic impedance of soft plastic layer; therefore, the effect of the interface is minimal. A square electrical pulse from the pulser–receiver unit is then launched into the pitching transducer with a central frequency of 5 MHz. The acoustic field transmitted through the tablet layer (e.g., DCL-14) is captured by the receiving (catch) transducer in contact with the other face of the layer (Fig. 5), and digitized as a waveform by the oscilloscope. For the Poisson’s ratio extraction, the reported procedure is applied to the same layers with 5 MHz shear wave transducers to acquire the transverse (shear) acoustic wave values of each layer. To determine the times of flight of pressure and shear waves, a Matlab 7.0.1 (The Mathworks, Natick, MA, USA) subroutine is used to record the time instants when the signal amplitude exceeds a threshold value set at three times the background ultrasonic noise level and saves these values as the arrival times of the pressure and shear waves. Processing of the acquired waveforms yields the TOF values of the longitudinal (pressure) ∆t_L and transverse (shear) acoustic waves ∆t_T values of each BL-tablet layer (Figs. 6 and 7). 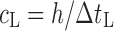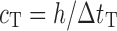The longitudinal and transverse phase velocities (c_L and c_T) can be related to ∆t_L and ∆t_T in the medium by and , respectively, where h is the distance traveled in the layer. 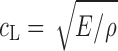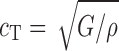c_L and c_T are a function of the mass density ρ of the propagation medium, the Young’s modulus E, and the shear modulus G of the medium, that is, and , respectively. From Figs. 6 and 7, the arrival times of ∆t_L and ∆t_T are measured and for a known layer thickness h, c_L, and c_T values are determined for each DCL-14 and MCC layers (Table II). The average mass densities of the DCL-14 (ρ_DCL) and the MCC (ρ_MCC) layers of the BL-tablet are determined from direct mass measurements (Table II). Using values of the Young’s moduli E and the shear moduli G, Poisson’s ratios ν of the DCL-14 and the MCC layers of the BL-tablet can be calculated by 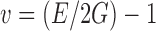. In the reported contact ultrasonic measurements, the sampling periods of the acquired signals are 200 ns and the oversampling rate set on the digitizing oscilloscope is set to 512. The extracted values of the Young’s modulus E and the Poisson’s ratio ν for each layer based on the contact ultrasonic measurements are used in the FE analysis to calculate the resonance frequencies of the BL-tablet. The values are to be compared to the resonance frequencies from the air-coupled acoustic experiments for verification purposes.

Fig. 5.

Schematic of the acoustic experimental set-up with a pair of 5-MHz transducers operating in pitch–catch mode (not to scale)

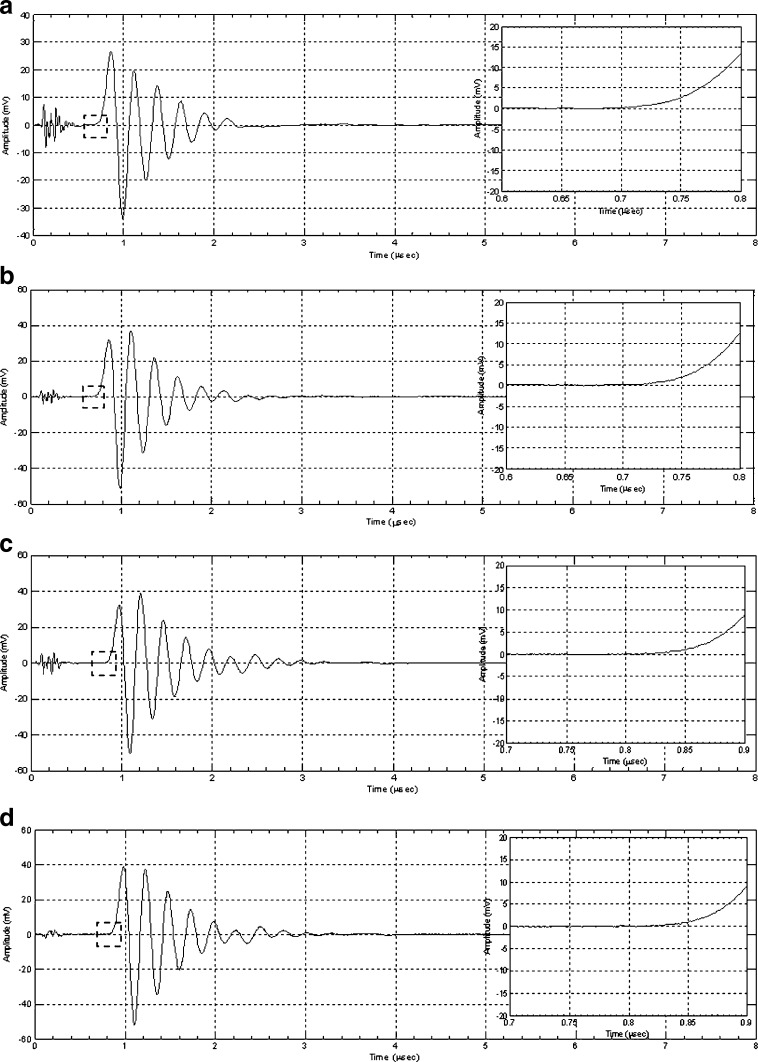
Fig. 6.

Longitudinal (pressure) acoustic waveforms for the DCL-14 a, b and MCC c, d layers of two BL-tablets and insets depict the TOF values of the longitudinal (0.7–0.8 μs) acoustic waves

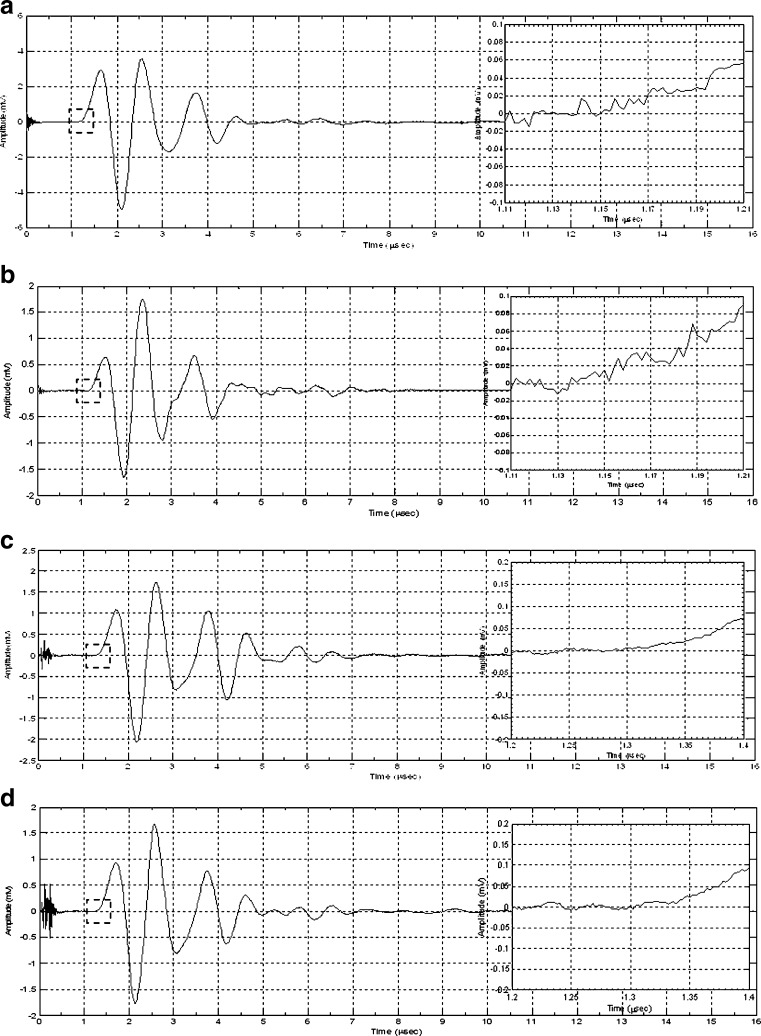
Fig. 7.

Transverse (shear) acoustic waveforms for the DCL-14 a, b and MCC c, d layers of two BL-tablets and insets depict the TOF values of the transverse (1.15–1.3 μs) acoustic waves

Table II.

Summary of the Mechanical Properties of the DCL-14 and the MCC Layers of the Sample Set

					Acoustic properties		Mechanical properties
Tablet No.	Layer	V (m3)	m (mg)	ρ (kg/m3)	c L (m/s)	c T (m/s)	E (GPa)	v	G (MPa)
Tablet01	DCL-14	120.43	149.12	1,238.22	2,142.85	1,315.31	5.69	0.33	2,142.17
	MCC	87.73	99.88	1,138.48	1,375.03	846.39	2.15	0.32	815.58
Tablet02	DCL-14	121.77	148.98	1,223.45	2,147.77	1,309.86	5.64	0.34	2,099.11
	MCC	87.94	100.19	1,139.33	1,373.28	845.32	2.15	0.32	814.13
Tablet03	DCL-14	120.14	149.28	1,242.55	2,143.46	1,316.47	5.71	0.33	2,153.46
	MCC	87.14	99.21	1,138.56	1,371.68	846.95	2.14	0.31	816.72
Tablet04	DCL-14	121.26	149.05	1,229.17	2,148.38	1,312.33	5.67	0.34	2,116.89
	MCC	88.02	100.23	1,138.71	1,370.31	845.12	2.14	0.32	813.30
Tablet05	DCL-14	120.29	149.19	1,240.25	2,143.41	1,316.91	5.70	0.33	2,150.91
	MCC	87.55	99.64	1,138.11	1,369.91	844.98	2.14	0.32	812.60
Tablet06	DCL-14	120.88	149.92	1,240.23	2,139.43	1,315.78	5.68	0.32	2,147.18
	MCC	87.03	99.11	1,138.79	1,374.75	846.15	2.15	0.32	815.34
Tablet07	DCL-14	120.79	149.58	1,238.35	2,140.29	1,308.25	5.67	0.34	2,119.46
	MCC	87.25	99.38	1,138.98	1,374.28	843.12	2.15	0.33	809.65
Tablet08	DCL-14	121.03	149.82	1,237.87	2,141.84	1,315.65	5.68	0.33	2,142.67
	MCC	88.02	100.24	1,138.87	1,371.14	842.26	2.14	0.32	807.92
Tablet09	DCL-14	121.83	148.86	1,221.86	2,139.36	1,314.25	5.59	0.32	2,110.46
	MCC	87.62	99.71	1,138.01	1,368.23	840.23	2.13	0.33	803.42
Tablet10	DCL-14	120.31	149.17	1,239.88	2,139.18	1,312.41	5.67	0.33	2,135.59
	MCC	87.36	99.46	1,138.51	1,369.82	845.21	2.14	0.32	813.33

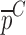is the determined mechanical property vector based on the contact ultrasonic measurements. V, m, and ρ values are extracted from direct mass density measurements and c _L, c _T are determined from TOF ultrasonic measurements for each BL-tablet layer

Finite Element Analysis for Bilayer Tablet Spectral Properties

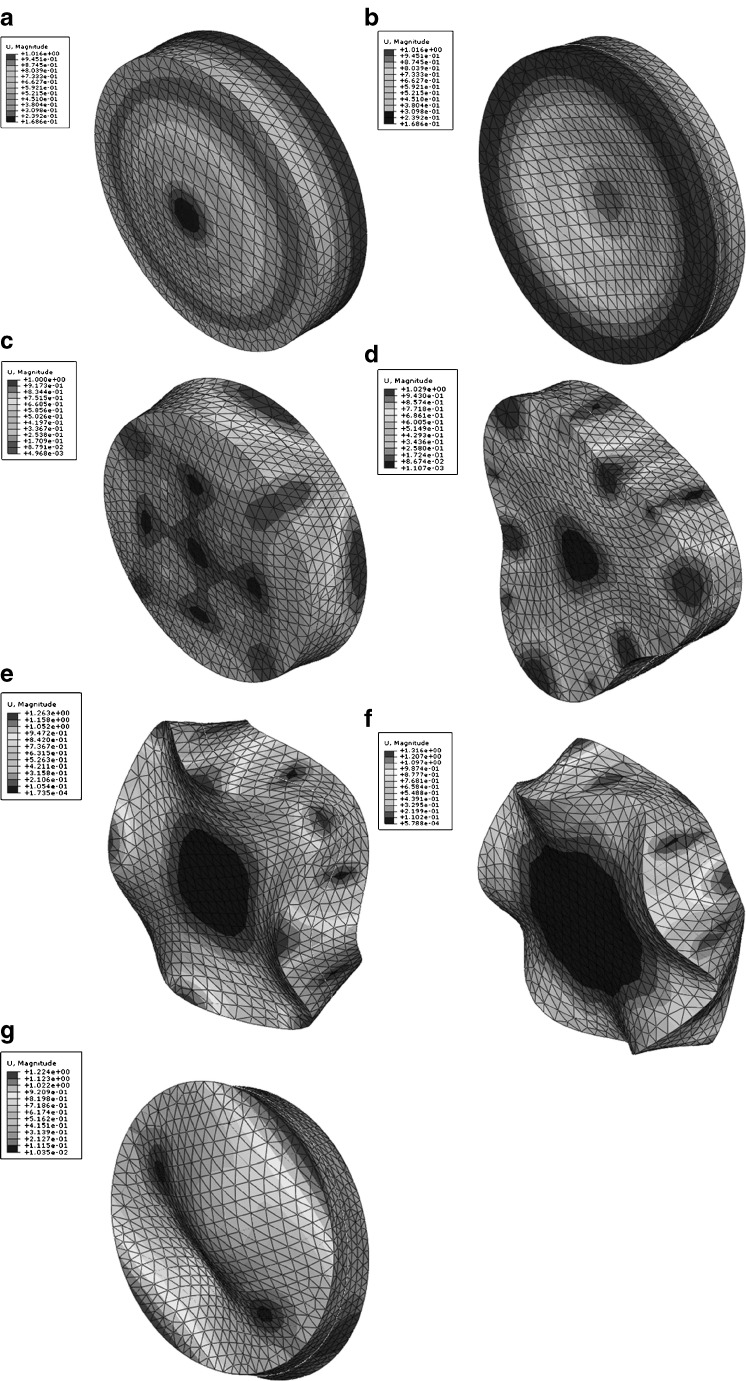
Resonance frequencies and corresponding mode shapes of the BL-tablet are related to its mechanical properties (e.g., Young’s moduli, Poisson’s ratios, and material mass densities of each layer) as well as its geometry (e.g., shape and dimensions of each layer) and defects. In the air-coupled acoustic technique, in order to extract the mechanical properties (i.e., Young’s modulus E, Poisson’s ratio ν and mass density ρ) of the DCL-14 and the MCC layers of the BL-tablet from its resonance frequencies, an iterative procedure based on Newton’s method and the FE method have been utilized (21,22). In the FE study employed for computing the resonance frequencies of the BL-tablet, the four-node linear tetrahedron element is used in the mesh generation for the BL-tablet. The three-dimensional mesh for the BL-tablet is developed consisting of two individual layers (DCL-14 and MCC). The number of elements, number of nodes, degrees of freedom, and typical element size in the FE mesh are 30,043, 8,607, 23,821, and 400 μm, respectively. The Lanczos eigenvalue solver implemented in the commercial software package ABAQUS (32) is employed to obtain the resonance frequencies and the mode shapes of the BL-tablet (Fig. 8) in the frequency range of 10–200 kHz for the given material properties.

Fig. 8.

Mode shapes of a BL-tablet for modes 10–11 (a), 12–13 (b), 14 (c), 15–16 (d), 17–18 (e), 19–20 (f) and 21–22 (g)

Computational Procedure for Extracting Bilayer Tablet Mechanical Properties

Resonance frequencies determined from the FE study are specified in the frequency range of 10–200 kHz which is consistent with the bandwidth of the air-coupled transducer used in the experiments (95–150 kHz). Using their resonance frequencies, Ε_DCL, ρ_DCL, ν_DCL, Ε_MCC, ρ_MCC, and ν_MCC for the sample set are then extracted using an iterative computational procedure such as Newton’s method (21,22). At each iteration step k, the values of the vector 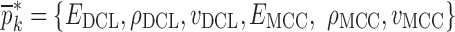of a BL-tablet is calculated for k = 0, 1, …, m. The final step of the iteration, m, corresponds to the termination of the iteration cycle. To start the computational process, a set of initial (estimate) values for this vector 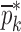(k = 0 for the initial step) is chosen (Table III) and the corresponding resonance frequency vector 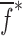is calculated via the FE method as reported in Table IV. To demonstrate the algorithm converges even if the initial estimates are considerably deviated from the actual values, a wide range for initial (estimate) values of mechanical properties is chosen. Each entry in the vector 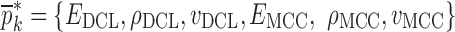and the vibrational mode numbers used in the analysis are denoted by indices i and j, respectively. At each iteration step k, a set of consistent six modes calculated from the FE study (j = 1, 2, …, 6) for 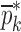are compared to the experimentally obtained six resonance frequencies vector 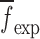(Table IV) for each BL-tablet. In the reported FE study, all the captured seven resonance frequencies and modes shapes are shown in the bandwidth of the air-coupled transducer, however, selected six resonance frequencies (modes 10–11, 12–13, 15–16, 17–18, 19–20, 21–22) are utilized for the iterative procedure. In calculating the sensitivity coefficient(s) (derivatives) s_j required for Newton’s method, the ith component of 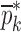is perturbed by a factor of (1 + ε), where ε is the perturbation parameter, and the resulting six perturbed mechanical property vectors denoted by 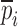(i = 1, 2, …, 6) are calculated. In computational results reported here, a typical value for ε is taken as ε = 0.005. In the absence of any intuition for choosing a value for ε, a trial-and-error method can narrow the possibilities to a reasonably small interval. The FE model is run for each 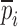to determine the corresponding six resonance frequency vectors 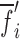and to calculate their shifts 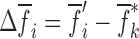due to their perturbations. Using the first term in Taylor’s expansion (Newton’s method), the sensitivity coefficient vector {s_j} is approximated for i = 1, 2, …, 6 by:

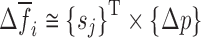1

Table III.

Summary of the Numerical Iteration Results for Each BL-Tablet Layer

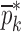
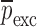
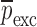
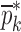
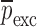
Tablet no.	Layer			Difference%			Difference%			Difference%
		ρ (kg/m3)	ρ (kg/m3)		v	v		E (GPa)	E (GPa)
Tablet01	DCL-14	1,708.75	1,235.18	38.34	0.45	0.33	37.19	7.96	5.68	40.16
	MCC	1,579.44	1,137.43	38.86	0.44	0.32	37.69	3.04	2.16	40.71
Tablet02	DCL-14	1,708.83	1,226.73	39.30	0.48	0.35	38.12	7.96	5.64	41.17
	MCC	1,586.42	1,135.43	39.72	0.43	0.31	38.53	3.03	2.14	41.61
Tablet03	DCL-14	1,715.81	1,239.21	38.46	0.45	0.33	37.31	8.01	5.71	40.29
	MCC	1,572.14	1,137.42	38.22	0.44	0.32	37.07	3.01	2.15	40.04
Tablet04	DCL-14	1,713.34	1,227.67	39.56	0.47	0.34	38.37	8.05	5.69	41.44
	MCC	1,578.64	1,138.17	38.71	0.43	0.31	37.54	2.99	2.13	40.54
Tablet05	DCL-14	1,728.99	1,238.89	39.56	0.46	0.33	38.37	8.08	5.71	41.44
	MCC	1,586.93	1,138.89	39.34	0.46	0.33	38.16	3.05	2.16	41.21
Tablet06	DCL-14	1,725.42	1,244.71	38.62	0.44	0.32	37.46	7.95	5.66	40.46
	MCC	1,577.84	1,139.07	38.52	0.43	0.31	37.36	3.00	2.14	40.35
Tablet07	DCL-14	1,724.28	1,244.43	38.56	0.47	0.34	37.40	7.97	5.68	40.40
	MCC	1,580.61	1,139.59	38.70	0.44	0.32	37.54	3.01	2.14	40.54
Tablet08	DCL-14	1,722.16	1,241.11	38.76	0.44	0.32	37.60	7.97	5.67	40.60
	MCC	1,579.77	1,137.18	38.92	0.45	0.33	37.75	3.01	2.14	40.77
Tablet09	DCL-14	1,712.03	1,228.67	39.34	0.46	0.33	38.16	7.92	5.61	41.21
	MCC	1,587.18	1,136.46	39.66	0.46	0.33	38.47	3.03	2.14	41.55
Tablet10	DCL-14	1,720.00	1,234.92	39.28	0.46	0.33	38.10	8.03	5.69	41.15
	MCC	1,580.35	1,138.42	38.82	0.45	0.33	37.66	3.05	2.17	40.67

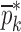is the vector of starting mechanical property for the iterative computational procedure, 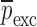is the extracted mechanical property vector upon completion of iterative procedure for 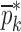for the sample set. Percentage differences of the initial and experimental mechanical property vectors are shown for each BL-Tablet layer

Table IV.

Summary of the Resonance Frequencies and Corresponding Mode Numbers for the Sample Set

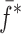
Modes		Tablet01			Tablet02			Tablet03			Tablet04			Tablet05			Difference (%)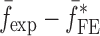
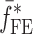
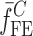
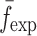
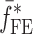
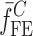
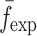
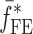
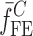
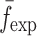
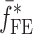
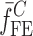
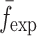
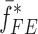
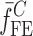
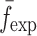
10–11	101.4	97.3	97.3	97.2	97.1	97.3	97.3	97.1	97.1	97.0	96.8	96.7	96.6	97.3	97.2	97.1	0.01–0.7
12–13	108.1	103.0	102.8	102.9	102.2	102.1	102.3	102.9	102.5	102.9	102.2	102.3	102.5	102.1	101.8	102.0	0.07–0.8
14	112.7	110.2	110.3	110.4	110.5	110.8	110.7	110.5	110.4	110.4	109.3	109.4	109.2	109.7	109.7	109.9	0.01–0.8
15–16	122.4	114.6	114.7	114.9	114.5	114.8	114.7	114.4	114.7	114.6	114.5	114.1	114.1	114.1	114.2	114.3	0.09–0.6
17–18	136.9	130.6	130.5	130.7	130.9	130.7	130.9	130.7	130.3	130.8	130.6	130.4	130.6	130.2	130.1	130.0	0.03–0.7
19–20	143.4	134.2	134.1	134.1	134.6	134.6	134.8	134.5	134.8	134.7	134.1	134.3	134.0	134.8	134.5	134.7	0.007–0.6
21–22	145.2	138.8	138.8	138.9	137.8	138.1	138.0	138.3	138.2	138.1	138.5	138.3	138.4	138.9	138.6	138.9	0.007–0.8
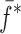
Modes		Tablet06			Tablet07			Tablet08			Tablet09			Tablet10			Difference (%)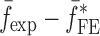
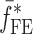
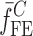
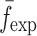
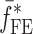
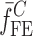
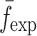
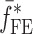
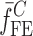
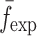
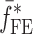
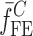
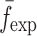
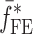
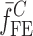
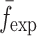
10–11	101.4	97.1	97.3	97.2	96.7	96.8	96.9	97.9	97.8	97.9	97.2	97.3	97.1	97.7	97.7	97.5	0.01–1.1
12–13	108.1	102.2	102.3	102.4	102.9	102.5	102.6	102.4	102.4	102.3	102.2	102.6	102.4	101.7	101.8	101.9	0.07–1.1
14	112.7	110.4	110.3	110.2	110.6	110.7	110.9	109.7	109.7	109.8	110.5	110.3	110.4	110.6	110.5	110.4	0.01–1.2
15–16	122.4	114.2	114.5	114.6	114.7	114.5	114.7	114.8	114.5	114.6	114.4	114.7	114.5	114.4	114.3	114.2	0.09–0.5
17–18	136.9	129.6	129.6	129.9	130.7	130.6	130.4	131.1	130.7	130.9	130.3	130.4	130.1	130.9	130.9	130.8	0.03–1.1
19–20	143.4	135.5	135.4	135.1	133.8	134.3	134.0	134.6	134.5	134.5	134.8	134.9	134.7	134.3	134.4	134.1	0.007–1.2
21–22	145.2	138.7	138.6	138.8	137.8	137.7	137.9	138.8	138.6	138.7	138.3	138.1	138.2	138.6	138.6	138.4	0.007–0.8

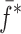is the resonance frequency vector corresponding to 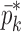, 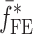and 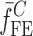are the FE-based resonance frequency vectors corresponding to 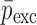and 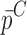, respectively. 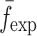is the resonance frequency vector directly measured for the sample set using air-coupled acoustic excitation set-up

where

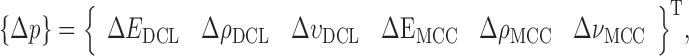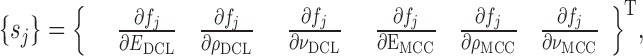j is the vibrational mode number, and {s_j} the sensitivity coefficient(s) (derivatives) vector. After running the FE model and applying Eq. (1) for i = 1, 2, …, 6 to calculate the sensitivity coefficients for six modes j = 1, 2, …, 6 (not necessarily sequential), the sensitivity tangent matrix 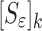is constructed for all six modes in the form of

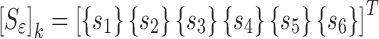2

Then, the change in mechanical property vector 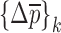due to the shift 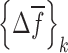in the selected set of resonance frequencies can be approximated by

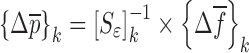3

where 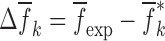, and 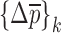the change in mechanical properties after the execution of an iteration step with a perturbation of 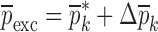when the change in the vector 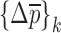values converge to zero or the singularity of the sensitivity tangent matrix 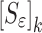is achieved.

RESULTS AND DISCUSSION

In the reported noncontact/nondestructive air-coupled acoustic measurements, the acquired waveforms and the corresponding frequency responses of the four BL-tablets from the sample set indicate that the responses of the tablets under the same excitation conditions are quite consistent (Figs. 3 and 4). For a given BL-tablet, a number of iterations are required to approximate the values of Young’s modulus Ε, Poisson’s ratio ν and mass density ρ for the layers of the tablet. In the extraction scheme, once the change in mechanical property vector 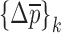values converge to zero or singularity of the sensitivity tangent matrix 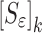, the iteration cycle is terminated at (k = m). The values of the mechanical property vector 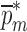used at the last (mth) iteration correspond to the extracted mechanical property vector 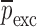of the DCL-14 and the MCC layers of the BL-tablet since 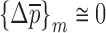. The numerical values for initial (estimate) mechanical property vector 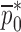and extracted mechanical property vector 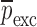for the sample set layers are listed in Table III. For comparison purposes, after extracting the mechanical properties for each layer of a BL-tablet, an FE analysis is conducted to calculate the corresponding resonance frequencies to extracted mechanical property vector 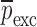. To validate the experimentally obtained resonance frequencies 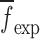of a BL-tablet, Young’s modulus (E_DCL and E_MCC) and Poisson’s ratio (ν_DCL and ν_MCC) values extracted from contact ultrasonic measurements and directly measured mass densities (ρ_DCL and ρ_MCC) of the sample set are also used in the FE analysis to determine the corresponding resonance frequencies 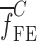of each BL-tablet (see Table IV for their numerical values). It is observed that in the frequency bandwidth of the air-coupled transducer (95–150 kHz) all the experimentally obtained resonance frequencies 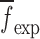of the sample set agree quantitatively well with the corresponding extracted FE resonance frequencies 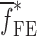for the 10^th–22nd modes (Table IV). Figure 8 shows the seven mode shapes (10th–22nd modes) of the BL-tablet in the 97.36–138.02 kHz frequency range. From the acquired mode shapes, it is observed that multiple modes and resonance frequencies occur for the 10th–11th, 12th–13th, 15th–16th, 17th–18th, 19th–20th, and 21st–22nd modes. This multiplicity is attributed to the non-symmetric mesh generation in the FE model of the BL-tablet. However, occurrence of the multiple modes has no relevant effect on the values of the FE resonance frequencies determined for the BL-tablet. It is noteworthy that as long as the modes used in the analysis are within the bandwidth of the air-coupled transducer, it is observed that the mode selected to be included in the iterative process is irrelevant to the analysis and its results.

The extracted Young’s modulus values for the MCC layers with porosity levels of 0.24–0.26 compare well with the findings reported in Roberts et al. (33) and Hancock et al. (12). Extracted Poisson’s ratio values of the MCC layers are also in good agreement as reported by Roberts et al. (33). High values of the extracted Young’s modulus values of DCL-14 are reasonable, since the initial layer (DCL-14) has been consolidated by the upper punch during the initial compaction creating a comparatively strong bonded tablet structure than the upper layer (MCC). During the manual debonding of the sample set from their interfaces, it is observed that the force needed to be used to debond a BL-tablet is much weaker than the applied compaction force employed during the compaction process. This could be attributed to the initial compression stage; the deformation within the initial layer (DCL-14) could be resulted in the accumulation of stored elastic strain which will be released upon removal of the rigid constraints (e.g., loaded-spring analogy). This mechanism will act as a stress concentrator and hence will cause a reduction in the strength of the interface. In addition, it is known that the retardation of particulate movement of the particles in contact with the die wall may cause the inherent bonding mechanisms such as particle interlocking (34) to be reduced and thus the energy required to be dissipated upon ejection may exceed the adhesive bond energy between the adjacent layers. Thus, the relaxation of the individual layers will not occur uniformly through the whole bilayer tablet which results in mechanical property anisotropy (35,36) in the tablet. Nondestructive acoustic testing and characterization can provide insight to these kind of arising complications during compaction of BL-tablets and other complex-shaped tablets (e.g., multilayered, enteric-coated, multi-layer coated, and dry-coated tablets) as well as it can also provide the defect state information of the layers, since the transient vibrational response of the tablet is strongly affected by mechanical defects (e.g., cracks, lamination, and capping) (23). During mechanical characterization, close vicinity of a test point at the tablet is acoustically noisy, and the tablet is subjected to mechanical vibrations. However, compared to the typical ranges of acoustic signals used in the reported approach, such environmental noises are much lower and, as a result, negligible.

To verify the air-coupled acoustic measurement results, contact ultrasonic measurements are conducted. In the contact ultrasonic method, the TOF data of the longitudinal (pressure) and transverse (shear) acoustic wave propagation in each BL-tablet layer is determined to extract the Young’s modulus and the Poisson’s ratio values. The acquired waveforms (Figs. 6 and 7) indicating TOF across the thickness of the sample set layers (DCL-14 and MCC) are consistent. As depicted in Fig. 6, the TOF values of the longitudinal (pressure) acoustic wave ∆t_L in the DCL-14 and the MCC layers of the BL-tablet01 are measured as Δt_L = 0.7 ± 0.01 μs (c_L = 2142.85 m/s) and Δt_L = 0.8 ± 0.01 μs (c_L = 1,375.03 m/s), respectively. The Poisson’s ratio and the shear modulus values are extracted using a pair of shear wave transducers. As depicted in Fig. 7, the TOF values of the transverse (shear) acoustic wave ∆t_T in the DCL-14 and the MCC layers of the BL-tablet01 are measured as Δt_T = 1.15 ± 0.01 μs (c_T = 1,315.31 m/s) and Δt_T = 1.3 ± 0.01 μs (c_T = 846.39 m/s), respectively. For known values of the material properties ρ_DCL, ρ_MCC, h_DCL, h_MCC, G_DCL, and G_MCC for each tablet, E_DCL, E_MCC, and ν_DCL, ν_MCC of the BL-tablet01 are extracted as 5.69 ± 0.02 GPa, 2.15 ± 0.01 GPa and 0.33 ± 0.01, 0.32 ± 0.01, respectively (Table II). It is found that the Young’s modulus and the Poisson’s ratio values extracted for the sample set from the air-coupled acoustic measurements are in good agreement with those determined from the contact ultrasonic measurements (Table V). The consistent values of the resonance frequencies of the sample set, using air-coupled acoustic experimental set-up 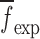and FE resonance frequencies 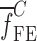based on the mechanical properties extracted from the contact ultrasonic and direct mass density measurements, also confirm the results of the Young’s modulus, Poisson’s ratio, and mass density values extracted from air-coupled acoustic experiments as a reasonably accurate method for determining such critical mechanical properties. To establish repeatability of measurements, contact pitch/catch ultrasonic experiments are conducted for the same debonded DCL-14 and MCC layers of the sample set at random dates (i.e., within a week), the coefficients of variation are calculated as 0.68% for the Young’s modulus and 0.31% for the Poisson’s ratio values. Since the tablet core is not coated, it is believed that air humidity might be a factor responsible for these small variations. However, in the current study, with the focus is on the measurement of the mechanical properties at room conditions, no systematic study for the effect of temperature and humidity on the mechanical properties of the BL-tablets is conducted.

Table V.

Summary of the Mechanical Property Comparison of the DCL-14 and the MCC Layers of the Sample Set Based on Air-Coupled Acoustic and Contact Ultrasonic Techniques. Percentage Differences of 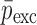and 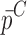are Shown for Each BL-Tablet Layer

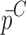
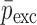
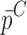
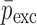
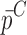
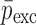
Tablet no.	Layer			Difference%			Difference%			Difference%
		ρ (kg/m3)	ρ (kg/m3)		v	v		E (GPa)	E (GPa)
Tablet01	DCL-14	1,238.22	1,235.18	0.25	0.33	0.33	0.00	5.69	5.68	0.18
	MCC	1,138.48	1,137.43	0.09	0.32	0.32	0.00	2.15	2.16	−0.46
Tablet02	DCL-14	1,223.45	1,226.73	−0.27	0.34	0.35	−2.86	5.64	5.64	0.00
	MCC	1,139.33	1,135.43	0.34	0.32	0.31	3.23	2.15	2.14	0.47
Tablet03	DCL-14	1,242.55	1,239.21	0.27	0.33	0.33	0.00	5.71	5.71	0.00
	MCC	1,138.56	1,137.42	0.10	0.31	0.32	−3.13	2.14	2.15	−0.47
Tablet04	DCL-14	1,229.17	1,227.67	0.12	0.34	0.34	0.00	5.67	5.69	−0.35
	MCC	1,138.71	1,138.17	0.05	0.32	0.31	3.23	2.14	2.13	0.47
Tablet05	DCL-14	1,240.25	1,238.89	0.11	0.33	0.33	0.00	5.70	5.71	−0.18
	MCC	1,138.11	1,138.89	−0.07	0.32	0.33	−3.03	2.14	2.16	−0.93
Tablet06	DCL-14	1,240.23	1,244.71	−0.36	0.32	0.32	0.00	5.68	5.66	0.35
	MCC	1,138.79	1,139.07	−0.02	0.32	0.31	3.23	2.15	2.14	0.47
Tablet07	DCL-14	1,238.35	1,244.43	−0.49	0.34	0.34	0.00	5.67	5.68	−0.18
	MCC	1,138.98	1,139.59	−0.05	0.33	0.32	3.13	2.15	2.14	0.47
Tablet08	DCL-14	1,237.87	1,241.11	−0.26	0.33	0.32	3.13	5.68	5.67	0.18
	MCC	1,138.87	1,137.18	0.15	0.32	0.33	−3.03	2.14	2.14	0.00
Tablet09	DCL-14	1,221.86	1,228.67	−0.55	0.32	0.33	−3.03	5.59	5.61	−0.36
	MCC	1,138.01	1,136.46	0.14	0.33	0.33	0.00	2.13	2.14	−0.47
Tablet10	DCL-14	1,239.88	1,234.92	0.40	0.33	0.33	0.00	5.67	5.69	−0.35
	MCC	1,138.51	1,138.42	0.01	0.32	0.33	−3.03	2.14	2.17	−1.38

CONCLUSIONS

The mechanical properties of a bilayer tablet play a critical role in defining its performance, disintegration profile, and mechanical integrity as a drug delivery device. Since the adjacent compacted layers of a bilayer tablet are bonded together by mechanical means, it is possible that mechanical properties of each layer can affect the therapeutic functions of the drug and their monitoring is essential to quality control. In the current study, for determining the mechanical properties of bilayer tablets, a noncontact/nondestructive air-coupled acoustic testing platform is described and demonstrated. A computational procedure based on the finite element method and Newton’s method for extracting the Young’s modulus, the Poisson’s ratio, and the mass density values from the measured resonance frequencies of a bilayer tablet is applied. It is established that the mechanical properties of a bilayer tablet can be extracted utilizing the experimental noncontact methodology and the iterative computational procedure based its measured resonance frequencies. A standard contact ultrasonic technique based on the time-of-flight measurements of the longitudinal (pressure) and transverse (shear) acoustic wave propagation in the debonded layers of a bilayer tablet is successfully conducted to verify the accuracy of the Young’s modulus and the Poisson’s ratio measurements based on the air-coupled method. It is found that the extracted mechanical properties from the air-coupled data agree well with those determined from contact measurements. It is also reported that experimentally acquired resonance frequencies agree quantitatively well with the FE-based resonance frequency predictions corresponding to the extracted mechanical properties from air-coupled and contact ultrasonic measurements. The major advantages of the current air-coupled acoustic characterization system include: (a) it is a noncontact/nondestructive technique, therefore the layered tablet can be re-examined at later times to monitor stability or used for further functional studies such as disintegration and content uniformity tests with prior knowledge of the quality and mechanical properties of individual layers; (b) initiation of weak bonding at the interface and defect state monitoring in the layers and/or at the interface of multilayered tablets may be possible, since the transient vibrational response of the tablet is strongly affected by mechanical defects (e.g., cracks, lamination, and capping); (c) operates in the microsecond time-scale (i.e., acoustic signal acquisition and processing is approximately 400 μs per tablet excluding time consumed for its handling); (d) applicability to different shapes (e.g., atypical, oval and capsule shapes) and types of tablets (e.g., multilayered, enteric-coated, multi-layer coated, and dry-coated tablets).