Table 1.

Model notation. provides a summary of notation.

List of notation
s(t)	proportion of population that is susceptible in the community at time t, s(t) ∈ [0, 1]
i(t)	proportion of population that is infectious in the community at time t, i(t) ∈ [0, 1]
r(t)	proportion of population that has recovered in the community at time t, r(t) ∈ [0, 1]
d(t)	v of population that has died in the community at time t, d(t) ∈ [0, 1]
x(t) = (s (t), i(t), r(t), d(t))	state that describes the disease status of a community
x(0) = (s (0), i(0), r(0), d(0))	initial disease state of a community
u(t)	decision variable to model NPI implementation, u(t) ∈ [0, b]
b	maximum reduction in infection rate β by NPI implementation, b ∈ [0, β]
T	time when vaccine becomes available, assumed to be exponential with mean Φ
β	infection rate
γ	recovery rate
τ	death rate
c	relative cost of NPI compared to a single death, c ∈ [0, 1]
R0	basic reproductive number, the average number of secondary cases an infectious individual case will cause
V (x; u)	value function defined as expected person-days lost
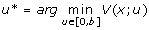	control that minimizes the value function
ψ (s, i)	switching curve
Ω ={(s, i); s, i ≥ 0, s + i ≤ 1}	state space
Ω1 = {(s, i) ∈ Ω, u* > 0}	state space where u* > 0
Ω2 = {(s, i) ∈ Ω, u* = 0 }	state space where u* = 0
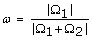	proportion of the control space
HJB	Hamilton-Jacobi-Bellman equation