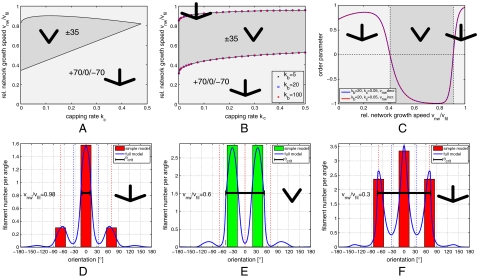
Figure 2.

Phase diagrams resulting from the rate equation approach. The dark and bright gray regions correspond to stability of the ± 35 and +70/0/-70 orientation patterns, respectively. (A) Analytical results from a linear stability analysis of the reduced model. (B) Numerical solution of the full model with three different branching rates k_b = {5,20,100}. (C) Evolution of the order parameter with changing network velocity v_nw from the numerical solution of the full model. The network behavior for increasing (red) and decreasing (blue) velocity are the same, thus the system is always in a stationary regime. (D, E, F) Comparison of the steady states of the analytically solved reduced model (bars) and the numerically solved full model (curves) for k_b = 20 and k_c = 0.05. Network bulk velocity v_nw is decreasing from D to F: (D) v_nw/v_fil = 0.98, (E) v_nw/v_fil = 0.6, and (F) v_nw/v_fil = 0.3. The vertical red and blue dotted lines mark the prominent angles +70/0/-70 and ± 35, respectively. The horizontal solid black line marks the orientation range |θ| ≤ θ_c in which single filaments are not outgrown by the bulk network.